In this paper, we put forward a hypothesis for turbulent kinetic energy, Reynolds stresses and scalar variance in wall-bounded turbulent flows, whereby these quantities, when normalized with the kinematic viscosity, mean turbulent energy dissipation rate and scalar dissipation rate, are independent of the Reynolds and Péclet numbers when they are sufficiently large. In particular, there exist two scaling ranges: (i) an inertial-convective range at sufficiently large distance from the wall over which a $2/3$ power-law scaling emerges for all quantities mentioned above; (ii) a viscous-convective range between the viscous-diffusive and inertial-convective ranges at large Prandtl number over which the normalized scalar variance is constant. The relatively large amount of available wall turbulence data either provides reasonably good support for this hypothesis or at least exhibits a trend that is consistent with the predictions of this hypothesis. The relationship between the proposed scaling and the traditional wall scaling is discussed. Possible ultimate statistical states of wall turbulence are also proposed.

The flow of three non-Newtonian fluids, comprising polymer and surfactant additives, in a periodically constricted tube (PCT) are experimentally compared. The radius of the tube walls is sinusoidal with respect to the streamwise direction. The three fluids are aqueous solutions of flexible polymers, rigid biopolymers and surfactants, which are typically used for drag-reduction in turbulent flows. Steady shear viscosity measurements demonstrate that rigid and flexible polymer solutions are shear-thinning, while surfactant solutions have a Newtonian and water-like shear viscosity. Capillary driven extensional rheology demonstrates that only flexible polymer solutions produce elastocapillary thinning. Particle shadow velocimetry is used to measure the velocity of each flow within the PCT at five Reynolds numbers spanning roughly 0.5 to 300. Relative to the Newtonian flows, rigid polymer solutions exhibit a blunt velocity profile. Flexible polymer solutions demonstrate a distinct chevron-shaped velocity contour and zones of opposing vorticity when the Deborah number exceeds 0.1. Using the vorticity transport equation, it is revealed that the opposing vorticity zones are coupled with a non-Newtonian torque. The PCT reveals that the surfactant solutions have similar non-Newtonian features as flexible polymer solutions – those being a chevron velocity pattern, opposing vorticity and a finite non-Newtonian torque. This observation is of practical importance since conventional shear and extensional rheometric measurements are not capable of demonstrating non-Newtonian features of the surfactant solutions. The investigation demonstrates that the PCT serves as a viable geometry for showing the non-Newtonian traits of dilute surfactant solutions.

This paper presents and compares two different approaches to solving the problem of wave propagation across a large finite periodic array of surface-piercing vertical barriers. Both approaches are formulated in terms of a pair of integral equations, one exact and based on a spacing $\delta > 0$ between adjacent barriers and the other approximate and based on a continuum model formally developed by using homogenisation methods for small $\delta$. It is shown that the approximate method is simpler to evaluate than the exact method which requires eigenvalues and eigenmodes related to propagation in an equivalent infinite periodic array of barriers. In both methods, the numerical effort required to solve problems is independent of the size of the array. The comparison between the two methods allows us to draw important conclusions about the validity of homogenisation models of plate array metamaterial devices. The practical interest in this problem stems from the result that for an array of barriers there exists a critical value of radian frequency, $\omega _c$, dependent on $\delta$, below which waves propagate through the array and above which it results in wave decay. When $\delta \to 0$, the critical frequency is given by $\omega _c = \sqrt {g/d}$, where $d$ is the plate submergence and $g$ is the acceleration due to gravity, which relates to the resonance in narrow channels and is an example of local resonance, studied extensively in metamaterials. The results have implications for proposed schemes to harness energy from ocean waves and other problems related to rainbow trapping and rainbow reflection.

Interaction of supercritical granular flow with obstacles in a confined channel generates shock waves characterised by a nearly parabolic front of agitated grains in the outer region and a heap of static grains in the inner region. The inner static heap results from granular collapse due to high volume fraction and enhanced collision rate near the obstacle. The present work reports interesting flow structures when granular shock waves are formed on an array of three identical triangular obstacles placed in a rectangular channel at different spacings. It is observed that spacing has a profound influence, resulting in three types of flow structures. Through dimensional analysis, it is found that the normalised shock stand-off distance primarily depends on the Froude number, $Fr$, and the normalised spacing between the wedges. The experimental data show a strong dependence on these parameters. The normalised shock stand-off distance decreases linearly for small $Fr$ and asymptotically approaches a small value at high $Fr$. The presence of a new stagnant dome-like structure results in a non-intuitive behaviour of shock stand-off with the wedge spacing. These features are discussed in detail using high-resolution shadowgraphy and the velocity field from particle image velocimetry.

Effects of surface tension reduction on wind-wave growth are investigated using direct numerical simulations of air–water two-phase turbulent flows. The incompressible Navier–Stokes equations for air and water sides are solved using an arbitrary Lagrangian–Eulerian method with boundary-fitted moving grids. The wave growth of finite-amplitude and non-breaking gravity–capillary waves, whose wavelength is less than 0.07 m, is simulated for two cases of different surface tensions under a low-wind-speed condition of several metres per second. The results show that significant wave height for the smaller surface tension case increases faster than that for the larger surface tension case. Energy fluxes for gravity and capillary wave scales reveal that when the surface tension is reduced, the energy transfer from the significant gravity waves to capillary waves decreases, and the significant waves accumulate more energy supplied by wind. This results in faster wave growth for the smaller surface tension case. The effect on the scalar transfer across the air–water interface is also investigated. The results show that the scalar transfer coefficient on the water side decreases due to the surface tension reduction. The decrease is caused by suppression of turbulence in the water side. In order to support the conjecture, the surface tension effect is compared with laboratory experiments in a small wind-wave tank.

It has been reported that, in submarine landslides down a slope, only a small part of the landslide momentum was transferred to the tsunami while most was lost in the further propagation over the flat bed. The high momentum of landslides off a slope meant a long run-out and a great impact on underwater infrastructure. Nevertheless, little attention has been paid to the variation of momentum of deformable submarine landslides off a slope, i.e. the loss of momentum when the slides flow away from the slope over a flat bottom. In this paper, the translational momentum of deformable submarine granular landslides running down a non-erodible inclined bed is investigated with a two-phase smoothed particle hydrodynamics model. After flowing down the slope, the transport rate and flux of the landslide translational momentum along the propagation over the flat bottom are examined. The effects of physical variables of the slide, particularly the grain size, the initial compaction and the front intrusion angle on the variation of the translational momentum, are explored. Accordingly, scaling relations of the spatial-temporal maximum transport rate and flux of the landslide translational momentum, as well as those of the slide final run-out and the generated leading wave height, are proposed. These scaling relations, although based on numerical data of small-scale granular landslides, demonstrate a preliminary attempt to develop practical expressions in the framework of momentum for estimating the run-out of real submarine landslides and the impact on underwater infrastructure.

We investigate the role of the laminar/turbulent interface in the interscale energy transfer in a boundary layer undergoing bypass transition with the aid of the Kármán–Howarth–Monin–Hill (KHMH) equation. A local binary indicator function is used to detect the interface and employed subsequently to define two-point intermittencies. These are used to decompose the standard-averaged interscale and interspace energy fluxes into conditionally averaged components. We find that the inverse cascade in the streamwise direction reported in an earlier work arises due to events across the downstream or upstream interfaces of a turbulent spot. However, the three-dimensional energy flux maps reveal significant differences between these two regions: in the downstream interface, inverse cascade is stronger and dominant over a larger range of streamwise and spanwise separations. We explain this finding by considering a propagating spot of simplified shape as it crosses a fixed streamwise location. We derive also the conditionally averaged KHMH equation, thus generalising similar equations for single-point statistics to two-point statistics. We compare the three-dimensional maps of the conditionally averaged production and total energy flux within turbulent spots against the maps of standard-averaged quantities within the fully turbulent region. The results indicate remarkable dynamical similarities between turbulent spots and the fully turbulent region for two-point statistics. This has been known only for single-point quantities, and we demonstrate here that the similarity extends to two-point quantities as well.

The sedimentation of two spherical solid objects in a viscous fluid has been extensively investigated and well understood. However, a pair of flat disks (in three dimensions) settling in the fluid shows more complex hydrodynamic behaviour. The present work aims to improve the understanding of this phenomenon by performing direct numerical simulation and physical experiments. The present results show that the sedimentation processes are significantly influenced by disk shape, characterized by a dimensionless moment of inertia I*, and Reynolds number Re of the leading disk. For the flatter disks with smaller I*, steady falling with enduring contact transits to periodic swinging with intermittent contacts as Re increases. The disks with larger I* tend to fall in a drafting-kissing-tumbling mode at low Re and to remain separated at high Re. Based on I* and Re, a phase diagram is created to classify the two-disk falling into ten distinctive patterns. The planar motion or three-dimensional motion of the disks is determined primarily by Re. Turbulent disturbance flows at a high Re contribute to the chaotic three-dimensional rotation of the disks. The chance for the two disks to contact is increased when I* and Re are reduced.

This paper investigates heat transport in penetrative convection with a marginally stable temporal-horizontal-averaged field or background field. Assuming that the background field is steady and is stabilised by the nonlinear perturbation terms, we obtain an eigenvalue problem with an unknown background temperature $\tau$ by truncating the nonlinear terms. Using a piecewise profile for $\tau$, we derived an analytical scaling law for heat transport in penetrative convection as $Ra\rightarrow \infty$: $Nu=(1/8)(1-T_M)^{5/3}Ra^{1/3}$ ($Nu$ is the Nusselt number; $Ra$ is the Rayleigh number and $T_M$ corresponds to the temperature at which the density is maximal). A conditional lower bound on $Nu$, under the marginal stability assumption, is then derived from a variational problem. All the solutions to the full system should deliver a higher heat flux than the lower bound if they satisfy the marginal stability assumption. However, data from the present direct numerical simulations and previous optimal steady solutions by Ding & Wu (J. Fluid Mech., vol. 920, 2021, A48) exhibit smaller $Nu$ than the lower bound at large $Ra$, indicating that these averaged fields are over-stabilised by the nonlinear terms. To incorporate a more physically plausible constraint to bound heat transport, an alternative approach, i.e. the quasilinear approach is invoked which delivers the highest heat transport and agrees well with Veronis's assumption, i.e. $Nu\sim Ra^{1/3}$ (Astrophys. J., vol. 137, 1963, p. 641). Interestingly, the background temperature $\tau$ yielded by the quasilinear approach can be non-unique when instability is subcritical.

The collision of a gravitationally driven horizontal current with a barrier following release from a confining lock is investigated using a shallow water model of the motion, together with a sophisticated boundary condition capturing the local interaction. The boundary condition permits several overtopping modes: supercritical, subcritical and blocked flow. The model is analysed both mathematically and numerically to reveal aspects of the unsteady motion and to compute the proportion of the fluid trapped upstream of the barrier. Several problems are treated. Firstly, the idealised problem of a uniform incident current is analysed to classify the unsteady dynamical regimes. Then, the extreme regimes of a very close or distant barrier are tackled, showing the progression of the interaction through the overtopping modes. Next, the trapped volume of fluid at late times is investigated numerically, demonstrating regimes in which the volume is determined purely by volumetric considerations, and others where transient inertial effects are significant. For a Boussinesq gravity current, even when the volume of the confined region behind the barrier is equal to the fluid volume, $30\,\%$ of the fluid escapes the domain, and a confined volume three times larger is required for the overtopped volume to be negligible. For a subaerial dam-break flow, the proportion that escapes is in excess of $60\,\%$ when the confined volume equals the fluid volume, and a barrier as tall as the initial release is required for negligible overtopping. Finally, we compare our predictions with experiments, showing a good agreement across a range of parameters.

Measurements of fluctuating wall pressure in a high-Reynolds-number flow over a body of revolution are described. With a strong axial pressure gradient and moderate lateral curvature, this non-equilibrium flow is relevant to marine applications as well as short-haul urban transportation. The wall-pressure spectrum and its scaling are discussed, along with its relation to the space–time structure. As the flow decelerates downstream, the root-mean-square level of the pressure drops together with the wall shear stress ($\tau _w$) and is consistently approximately 7$\tau _w$. While the associated dimensional spectra see a broadband reduction of over 15 dB per Hz, they appear to attain a single functional form, collapsing to within 2 dB when normalized with the wall-wake scaling where $\tau _w$ is the pressure scale and $U_e/\delta$ is the frequency scale. Here, $\delta$ is the boundary layer thickness and $U_e$ is the local free-stream velocity. The general success of the wall-wake scaling, including in the viscous $f^{-5}$ region, suggests that the large-scale motions in the outer layer play a predominant role in the near-wall turbulence and wall pressure. On investigating further, we find that the instantaneous wall-pressure fluctuations are characterized by a quasi-periodic feature that appears to convect downstream at speeds consistent with the outer peak in the turbulence stresses. The conditional structure of this feature, estimated through peak detection in the time series, resembles that of a roller, supporting the embedded shear layer hypothesis (Schatzman & Thomas, J. Fluid Mech., vol. 815, 2017, pp. 592–642; Balantrapu et al., J. Fluid Mech., vol. 929, 2021, A9). Therefore, the outer-region shear-layer-type motions may be important when devising strategies for flow control, drag and noise reduction for decelerating boundary layers.

We conduct wall-modelled large-eddy simulation (WMLES) of a pressure-driven three-dimensional turbulent boundary layer developing on the floor of a bent square duct to investigate the predictive capability of three widely used wall models, namely, a simple equilibrium stress model, an integral non-equilibrium model, and a partial differential equation (PDE) non-equilibrium model. The numerical results are compared with the experiment of Schwarz & Bradshaw (J. Fluid Mech., vol. 272, 1994, pp. 183–210). While the wall-stress magnitudes predicted by the three wall models are comparable, the PDE non-equilibrium wall model produces a substantially more accurate prediction of the wall-stress direction, followed by the integral non-equilibrium wall model. The wall-stress direction from the wall models is shown to have separable contributions from the equilibrium stress part and the integrated non-equilibrium effects, where how the latter is modelled differs among the wall models. The triangular plot of the wall-model solution reveals different capabilities of the wall models in representing variation of flow direction along the wall-normal direction. In contrast, the outer LES solution is unaffected by the type of wall model used, resulting in nearly identical predictions of the mean and turbulent statistics in the outer region for all the wall models. This is explained by the vorticity dynamics and the inviscid skewing mechanism of generating the mean three-dimensionality. Finally, the LES solution in the outer layer is used to study the anisotropy of turbulence. In contrast to the canonical two-dimensional wall turbulence, the Reynolds stress anisotropy exhibits strong non-monotonic behaviour with increasing wall distance.

Reinforcement learning is applied to the development of control strategies in order to reduce skin friction drag in a fully developed turbulent channel flow at a low Reynolds number. Motivated by the so-called opposition control (Choi et al., J. Fluid Mech., vol. 253, 1993, pp. 509–543), in which a control input is applied so as to cancel the wall-normal velocity fluctuation on a detection plane at a certain distance from the wall, we consider wall blowing and suction as a control input, and its spatial distribution is determined by the instantaneous streamwise and wall-normal velocity fluctuations at distance 15 wall units above the wall. A deep neural network is used to express the nonlinear relationship between the sensing information and the control input, and it is trained so as to maximize the expected long-term reward, i.e. drag reduction. When only the wall-normal velocity fluctuation is measured and a linear network is used, the present framework reproduces successfully the optimal linear weight for the opposition control reported in a previous study (Chung & Talha, Phys. Fluids, vol. 23, 2011, 025102). In contrast, when a nonlinear network is used, more complex control strategies based on the instantaneous streamwise and wall-normal velocity fluctuations are obtained. Specifically, the obtained control strategies switch abruptly between strong wall blowing and suction for downwelling of a high-speed fluid towards the wall and upwelling of a low-speed fluid away from the wall, respectively. Extracting key features from the obtained policies allows us to develop novel control strategies leading to drag reduction rates as high as 37 %, which is higher than the 23 % achieved by the conventional opposition control at the same Reynolds number. Finding such an effective and nonlinear control policy is quite difficult by relying solely on human insights. The present results indicate that reinforcement learning can be a novel framework for the development of effective control strategies through systematic learning based on a large number of trials.

We simulated the motions and interactions of circular squirmers under gravity in a two-dimensional channel at finite fluid inertia, aiming to provide a comprehensive analysis of the dynamic features of swimming microorganisms or engineered microswimmers. In addition to a squirmer-type factor (β), another control parameter (α) was introduced, representing ratio of the self-propelling strength to the sedimentation strength of squirmers. Simulations were performed at 0.4 ≤ α ≤ 1.2 and −5 ≤ β ≤ 5. We first considered the sedimentation of a single squirmer. Five patterns were revealed, depending on both α and β: steady downward falling, steady inclined falling or rising and small-scale or large-scale oscillating. Compared with a pusher (β < 0, gaining thrust from rear), a puller (β > 0, gaining thrust from front) is more likely to break down its symmetrical structure and subsequently lose stability, owing to the high-pressure regions on its lateral sides. Typically, a pusher settles faster than a puller, whereas a neutral squirmer (β = 0) settles in between. This is related to the ‘trailing negative flow’ behind a pusher and ‘leading negative flow’ before a puller. We then placed two squirmers in line with the gravity direction to study their interactions. Results show pullers attract each other and come into contact as a result of the low-pressure regions between them, whereas the opposite is observed for pushers. The interactions between two pullers are illustrated by their respective patterns. In contrast, pushers never come into contact and maintain distance from each other with increasing separation. We finally examined how a puller interacts with a pusher.

We consider the time evolution of a sessile drop of volatile partially wetting liquid on a rigid solid substrate. The drop evaporates under strong confinement, namely, it sits on one of the two parallel plates that form a narrow gap. First, we develop an efficient mesoscopic long-wave description in gradient dynamics form. It couples the diffusive dynamics of the vertically averaged vapour density in the narrow gap to an evolution equation for the profile of the volatile drop. The underlying free energy functional incorporates wetting, interface and bulk energies of the liquid and gas entropy. The model allows us to investigate the transition between diffusion-limited and phase transition-limited evaporation for shallow droplets. Its gradient dynamics character allows for a long-wave as well as a full-curvature formulation. Second, we compare results obtained with the mesoscopic long-wave model to corresponding direct numerical simulations solving the Stokes equation for the drop coupled to the diffusion equation for the vapour as well as to selected experiments. In passing, we discuss the influence of contact line pinning.

This paper presents a novel theoretical framework in the Hamiltonian theory of nonlinear surface gravity waves. The envelope of surface elevation and the velocity potential on the free water surface are introduced in the framework, which are shown to be a new pair of canonical variables. Using the two envelopes as the main unknowns, coupled envelope evolution equations (CEEEs) are derived based on a perturbation expansion. Similar to the high-order spectral method, the CEEEs can be derived up to arbitrary order in wave steepness. In contrast, they have a temporal scale as slow as the rate of change of a wave spectrum and allow for the wave fields prescribed on a computational (spatial) domain with a much larger size and with spacing longer than the characteristic wavelength at no expense of accuracy and numerical efficiency. The energy balance equation is derived based on the CEEEs. The nonlinear terms in the CEEEs are in a form of the separation of wave harmonics, due to which an individual term is shown to have clear physical meanings in terms of whether or not it is able to force free waves that obey the dispersion relation. Both the nonlinear terms that can only lead to the forcing of bound waves and those that are capable of forcing free waves are demonstrated, in the case of the latter through the analysis of the quartet and quintet resonant interactions of linear waves. The relations between the CEEEs and two other existing theoretical frameworks are established, including the theory for a train of Stokes waves up to second order in wave steepness (Fenton, ASCE J. Waterway Port Coastal Ocean Engng, vol. 111, issue 2, 1985, pp. 216–234) and a semi-analytical framework for three-dimensional weakly nonlinear surface waves with arbitrary bandwidth and large directional spreading by Li & Li (Phys. Fluids, vol. 33, issue 7, 2021, 076609).

Hydrodynamic clogging in planar channels is studied via direct numerical simulation for the first time, utilising a novel numerical test cell and stochastic methodology with special focus on the influence of electrostatic forces. Electrostatic physics is incorporated into an existing coupled lattice Boltzmann-discrete element method framework, which is verified rigorously. First, the dynamics of the problem is governed by the Stokes number, $St$. At low 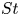$St$, the clogging probability, 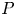$P$, increases with $St$ due to increasing collision frequency. At high $St$, however, 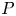$P$ decreases with 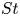$St$ due to quadratic scaling of hydrodynamic force acting on arches. Under electrostatic forces, clogging is well represented by the wall adhesion number, 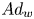$Ad_w$. For 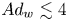$Ad_w \lesssim 4$, the mechanical dependence on 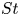$St$ is exhibited, while for 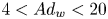$4 < Ad_w < 20$, there is a transition to high 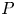$P$ as sliding along, and attachment to, the channel surface occurs increasingly. For $Ad_w \gtrsim 20$, clogging occurs with 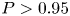$P > 0.95$. Particle agglomeration, however, can also decrease 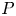$P$ due to diminished interaction with channel walls. Distinct parametric regions of clogging are also observed in relation to the channel width, while a critical width 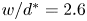$w/d^*=2.6$ is reported, which increases to 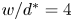$w/d^*=4$ with strong electrostatic surface attachment. The number of particles that form stable arches across a planar channel is determined to be 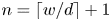$n=\left \lceil {w/d}\right \rceil + 1$. Finally, sensitivity to the Coulomb friction coefficient is determined in favour of calibrating numerical parameters to bulk system behaviour. The greatest sensitivities occur in situations where the arch stability is lowest, while clogging becomes independent of friction for strong wall adhesion.

Sea ice is crucial in many natural processes and human activities. Understanding the dynamical couplings between the inception, growth and equilibrium of sea ice and the rich fluid mechanical processes occurring at its interface and interior is of relevance in many domains, ranging from geophysics to marine engineering. Here we investigate experimentally the complete freezing process of water with dissolved salt in a standard natural convection system, i.e. the prototypical Rayleigh–Bénard cell. Due to the presence of a mushy phase, the studied system is considerably more complex than the freezing of fresh water in the same conditions (Wang et al., Proc. Natl Acad. Sci. USA, vol. 118, issue 10, 2021, e2012870118). We measure the ice thickness and porosity at the dynamical equilibrium state for different initial salinities of the solution and temperature gaps across the cell. These observables are non-trivially related to the controlling parameters of the system as they depend on the heat transport mode across the cell. We identify in the experiments five out of the six possible modes of heat transport. We highlight the occurrence of brine convection through the mushy ice and of penetrative convection in stably stratified liquid underlying the ice. A one-dimensional multi-layer heat flux model built on the known scaling relations of global heat transport in natural convection systems in liquids and porous media is proposed. Given the measured porosity of the ice, it allows us to predict the corresponding ice thickness, in a unified framework.

Lagrangian averaging plays an important role in the analysis of wave–mean-flow interactions and other multiscale fluid phenomena. The numerical computation of Lagrangian means, e.g. from simulation data, is, however, challenging. Typical implementations require tracking a large number of particles to construct Lagrangian time series, which are then averaged using a low-pass filter. This has drawbacks that include large memory demands, particle clustering and complications of parallelisation. We develop a novel approach in which the Lagrangian means of various fields (including particle positions) are computed by solving partial differential equations (PDEs) that are integrated over successive averaging time intervals. We propose two strategies, distinguished by their spatial independent variables. The first, which generalises the algorithm of Kafiabad (J. Fluid Mech., vol. 940, 2022, A2), uses end-of-interval particle positions; the second uses directly the Lagrangian mean positions. The PDEs can be discretised in a variety of ways, e.g. using the same discretisation as that employed for the governing dynamical equations, and solved on-the-fly to minimise the memory footprint. We illustrate the new approach with a pseudo-spectral implementation for the rotating shallow-water model. Two applications to flows that combine vortical turbulence and Poincaré waves demonstrate the superiority of Lagrangian averaging over Eulerian averaging for wave–vortex separation.

We introduce a new approach for modelling the swelling, drying and elastic behaviour of hydrogels, which leverages the tractability of classical linear-elastic theory whilst incorporating nonlinearities arising from large swelling strains. Relative to a reference state of a fully swollen gel, in which the polymer scaffold may only comprise less than $1\,\%$ of the total volume, a constitutive model for the Cauchy stress tensor is presented, which linearises around small deviatoric strains corresponding to shearing deformations of the material whilst allowing for a nonlinear relation between stress and isotropic strains. Such isotropic strains are considered only to be a consequence of losses and gains of water, while the hydrogel is taken to be instantaneously incompressible. The dynamics governing swelling and drying are described by coupling the interstitial flow of the water through the porous gel with the elastic response of the gel. This approach allows for a complete description of gel behaviour using only three macroscopic polymer-fraction-dependent parameters: an osmotic modulus, a shear modulus and a permeability. It is shown how these three material parameters can, in principle, be determined experimentally using a simple rheometry experiment in which a gel is compressed between two plates surrounded by water and the total force on the top plate is measured. To illustrate our approach, we solve for the swelling of a gel under horizontal confinement and for a partially dried hydrogel bead placed in water.