Let P*(α, β) denote the class of functions
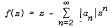
analytic and univalent in |z| < 1 for which
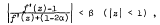
where α є [0, 1), β є (0, 1].
Sharp results concerning coefficients, distortion theorem and radius of convexity for the class P*(α, β) are determined. A comparable theorem for the classes C*(α, β) and P*(α, β) is also obtained. Furthermore, it is shown that the class P*(α, ß) is closed under ‘arithmetic mean’ and ‘convex linear combinations’.