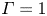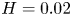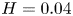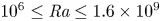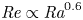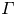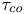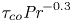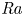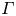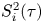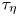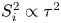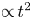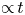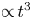We report on Lagrangian statistics of turbulent Rayleigh–Bénard convection under very different conditions. For this, we conducted particle tracking experiments in a  $H=1.1$-m-high cylinder of aspect ratio
$H=1.1$-m-high cylinder of aspect ratio 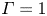 $\varGamma =1$ filled with air (Pr = 0.7), as well as in two rectangular cells of heights
$\varGamma =1$ filled with air (Pr = 0.7), as well as in two rectangular cells of heights 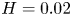 $H=0.02$ m (
$H=0.02$ m ( $\varGamma =16$) and
$\varGamma =16$) and 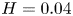 $H=0.04$ m (
$H=0.04$ m ( $\varGamma =8$) filled with water (Pr = 7.0), covering Rayleigh numbers in the range
$\varGamma =8$) filled with water (Pr = 7.0), covering Rayleigh numbers in the range 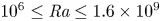 $10^6\le {\textit {Ra}}\le 1.6\times 10^9$. Using the Shake-The-Box algorithm, we have tracked up to 500 000 neutrally buoyant particles over several hundred free-fall times for each set of control parameters. We find the Reynolds number to scale at small Ra (large Pr) as
$10^6\le {\textit {Ra}}\le 1.6\times 10^9$. Using the Shake-The-Box algorithm, we have tracked up to 500 000 neutrally buoyant particles over several hundred free-fall times for each set of control parameters. We find the Reynolds number to scale at small Ra (large Pr) as 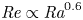 $ {\textit{Re}} \propto {\textit{Ra}}^{0.6}$. Further, the averaged horizontal particle displacement is found to be universal and exhibits a ballistic regime at small times and a diffusive regime at larger times, for sufficiently large
$ {\textit{Re}} \propto {\textit{Ra}}^{0.6}$. Further, the averaged horizontal particle displacement is found to be universal and exhibits a ballistic regime at small times and a diffusive regime at larger times, for sufficiently large 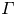 $\varGamma$. The diffusive regime occurs for time lags larger than
$\varGamma$. The diffusive regime occurs for time lags larger than 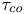 $\tau _{co}$, which is the time scale related to the decay of the velocity autocorrelation. Compensated as
$\tau _{co}$, which is the time scale related to the decay of the velocity autocorrelation. Compensated as 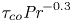 $\tau _{co} {\textit {Pr}}^{-0.3}$, this time scale is universal and rather independent of
$\tau _{co} {\textit {Pr}}^{-0.3}$, this time scale is universal and rather independent of 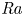 $ {\textit {Ra}}$ and
$ {\textit {Ra}}$ and 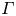 $\varGamma$. We have also investigated the Lagrangian velocity structure function
$\varGamma$. We have also investigated the Lagrangian velocity structure function 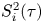 $S^2_i(\tau )$, which is dominated by viscous effects for times smaller than the Kolmogorov time
$S^2_i(\tau )$, which is dominated by viscous effects for times smaller than the Kolmogorov time 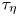 $\tau _\eta$ and hence
$\tau _\eta$ and hence 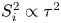 $S^2_i\propto \tau ^2$. For larger times we find a novel scaling for the different components with exponents smaller than what is expected in the inertial range of homogeneous isotropic turbulence without buoyancy. Studying particle-pair dispersion, we find a Batchelor scaling (
$S^2_i\propto \tau ^2$. For larger times we find a novel scaling for the different components with exponents smaller than what is expected in the inertial range of homogeneous isotropic turbulence without buoyancy. Studying particle-pair dispersion, we find a Batchelor scaling (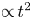 ${\propto }\,t^2$) on small time scales, diffusive scaling (
${\propto }\,t^2$) on small time scales, diffusive scaling (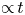 ${\propto }\,t$) on large time scales and Richardson-like scaling (
${\propto }\,t$) on large time scales and Richardson-like scaling (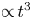 ${\propto }\,t^3$) for intermediate time scales.
${\propto }\,t^3$) for intermediate time scales.