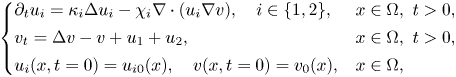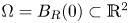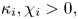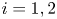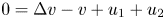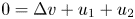We consider the global existence for the following fully parabolic chemotaxis system with two populations\[\left\{ \begin{array}{@{}ll} \partial_tu_i=\kappa_i\Delta u_i-\chi_i\nabla\cdot(u_i\nabla v),\quad i\in\{1,2\}, & x\in\Omega,\ t>0, \\ v_t=\Delta v-v+u_1+u_2, & x\in\Omega,\ t>0,\\ u_i(x,t=0)=u_{i0}(x),\quad v(x,t=0)=v_0(x), & x\in\Omega, \end{array} \right. \]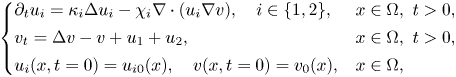
where $\Omega =\mathbb {R}^2$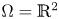 or $\Omega =B_R(0)\subset \mathbb {R}^2$
or $\Omega =B_R(0)\subset \mathbb {R}^2$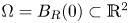 supplemented with homogeneous Neumann boundary conditions, $\kappa _i,\chi _i>0,$
supplemented with homogeneous Neumann boundary conditions, $\kappa _i,\chi _i>0,$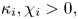 $i=1,2$
$i=1,2$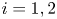 . The global existence remains open for the fully parabolic case as far as the author knows, while the existence of global solution was known for the parabolic-elliptic reduction with the second equation replaced by $0=\Delta v-v+u_1+u_2$
. The global existence remains open for the fully parabolic case as far as the author knows, while the existence of global solution was known for the parabolic-elliptic reduction with the second equation replaced by $0=\Delta v-v+u_1+u_2$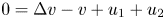 or $0=\Delta v+u_1+u_2$
or $0=\Delta v+u_1+u_2$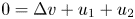 . In this paper, we prove that there exists a global solution if the initial masses satisfy the certain sub-criticality condition. The proof is based on a version of the Moser–Trudinger type inequality for system in two dimensions.
. In this paper, we prove that there exists a global solution if the initial masses satisfy the certain sub-criticality condition. The proof is based on a version of the Moser–Trudinger type inequality for system in two dimensions.
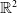 $\mathbb{R}^{2}$
$\mathbb{R}^{2}$