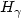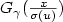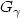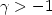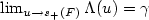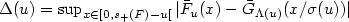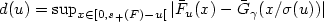Let F be a distribution function (d.f) in the domain of attraction of an extreme value distribution ${ H_{\gamma} }$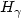; it is well-known that Fu(x), where Fu is the d.f of the excesses over u, converges, when u tends to s+(F), the end-point of F, to $G_{\gamma}(\frac{x}{\sigma(u)})$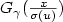, where $G_{\gamma}$ 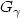is the d.f. of the Generalized Pareto Distribution. We provide conditions that ensure that there exists, for $\gamma >-1$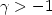, a function Λ which verifies $\lim_{u \rightarrow s_+(F)} \Lambda (u) =\gamma$ 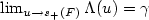and is such that $\Delta(u)= \sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\Lambda(u)} (x/ \sigma(u))| $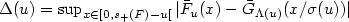converges to 0 faster than $d(u)=\sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\gamma}(x/ \sigma(u))|$.

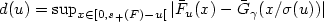We analyze the convergence of the prox-regularization algorithmsintroduced in [1], to solve generalized fractional programs,without assuming that the optimal solutions set of the consideredproblem is nonempty, and since the objective functions arevariable with respect to the iterations in the auxiliary problemsgenerated by Dinkelbach-type algorithms DT1 and DT2, we considerthat the regularizing parameter is also variable. On the otherhand we study the convergence when the iterates are onlyηk -minimizers of the auxiliary problems. This situation ismore general than the one considered in [1]. We also give someresults concerning the rate of convergence of these algorithms,and show that it is linear and some times superlinear for someclasses of functions. Illustrations by numerical examples aregiven in [1].