Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T20:40:06.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Penultimate approximation for the distribution of the excesses

Published online by Cambridge University Press:  15 November 2002

Rym Worms
Rym Worms*
Affiliation:
Université de Marne-la-Vallée, Équipe d'Analyse et de Mathématiques Appliquées, 5 boulevard Descartes, Champs-sur-Marne, 77454 Marne-la-Vallee Cedex 2, France; [email protected].
Get access

Abstract

Let F be a distribution function (d.f) in the domain of attraction of an extreme value distribution ${ H_{\gamma} }$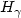; it is well-known that Fu(x), where Fu is the d.f of the excesses over u, converges, when u tends to s+(F), the end-point of F, to $G_{\gamma}(\frac{x}{\sigma(u)})$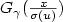, where $G_{\gamma}$ 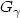is the d.f. of the Generalized Pareto Distribution. We provide conditions that ensure that there exists, for $\gamma >-1$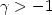, a function Λ which verifies $\lim_{u \rightarrow s_+(F)} \Lambda (u) =\gamma$ 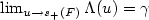and is such that $\Delta(u)= \sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\Lambda(u)} (x/ \sigma(u))| $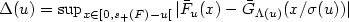converges to 0 faster than $d(u)=\sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\gamma}(x/ \sigma(u))|$.

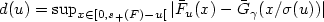Keywords

Generalized Pareto Distributionexcessespenultimate approximationrate of convergence.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 6: New directions in Time Series Analysis (Guest Editor: Philippe Soulier)New directions in Time Series Analysis (Guest Editor: Philippe Soulier) , 2002 , pp. 21 - 31
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balkema, A. and de Haan, L., Residual life time at great age. Ann. Probab. 2 (1974) 792-801. CrossRef
C.M. Goldie, N.H. Bingham and J.L. Teugels, Regular variation. Cambridge University Press (1987).
Cohen, J.P., Convergence rates for the ultimate and penultimate approximations in extreme-value theory. Adv. Appl. Prob. 14 (1982) 833-854. CrossRef
Fisher, R.A. and Tippet, L.H.C., Limiting forms of the frequency of the largest or smallest member of a sample. Proc. Cambridge Phil. Soc. 24 (1928) 180-190. CrossRef
Gomes, M.I., Penultimate limiting forms in extreme value theory. Ann. Inst. Stat. Math. 36 (1984) 71-85. CrossRef
Gomes, I. and de Haan, L., Approximation by penultimate extreme value distributions. Extremes 2 (2000) 71-85. CrossRef
M.I. Gomes and D.D. Pestana, Non standard domains of attraction and rates of convergence. John Wiley & Sons (1987) 467-477.
Pickands III, J., Statistical inference using extreme order statistics. Ann. Stat. 3 (1975) 119-131.
J.-P. Raoult and R. Worms, Rate of convergence for the Generalized Pareto approximation of the excesses (submitted).
R. Worms, Vitesse de convergence de l'approximation de Pareto Généralisée de la loi des excès. Preprint Université de Marne-la-Vallée (10/2000).
R. Worms, Vitesses de convergence pour l'approximation des queues de distributions Ph.D. Thesis Université de Marne-la-Vallée (2000).