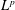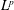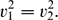2 results
Sharp Bounds for Oscillatory Integral Operators with Homogeneous Polynomial Phases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 771-786
- Print publication:
- December 2020
-
- Article
- Export citation
-
We obtain sharp
$L^{p}$ bounds for oscillatory integral operators with generic homogeneous polynomial phases in several variables. The phases considered in this paper satisfy the rank one condition that is an important notion introduced by Greenleaf, Pramanik, and Tang. Under certain additional assumptions, we can establish sharp damping estimates with critical exponents to prove endpoint 
$L^{p}$ estimates.
Stability of weakly dissipative Reissner–Mindlin–Timoshenko plates: A sharp result
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 27 April 2017, pp. 226-252
-
- Article
- Export citation
-
In the present article, we show that there exists a critical number that stabilizes the Reissner–Mindlin–Timoshenko system with frictional dissipation acting on rotation angles. We identify two speed characteristics v12:=K/ρ1 and v22:=D/ρ2, and we show that the system is exponentially stable if and only if
For v12 ≠ v22, we prove that the system is polynomially stable and determine an optimal estimate for the decay. To confirm our analytical results, we compute the numerical solutions by means of several numerical experiments by using a finite difference method.
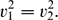\begin{equation*}
v_{1}^{2}=v_{2}^{2}.
\end{equation*}
