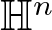1 results
Local regularity for nonlocal double phase equations in the Heisenberg group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-37
-
- Article
-
- You have access
- HTML
- Export citation
-
We prove interior boundedness and Hölder continuity for the weak solutions of nonlocal double phase equations in the Heisenberg group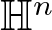
$\mathbb{H}^n$. This solves a problem raised by Palatucci and Piccinini et al. in 2022 and 2023 for the nonlinear integro-differential problems in Heisenberg setting. Our proof of the a priori estimates bases on De Giorgi–Nash–Moser theory, where the important ingredients are Caccioppoli-type inequality and Logarithmic estimate. To achieve this goal, we establish a new and crucial Sobolev–Poincaré type inequality in local domain, which may be of independent interest and potential applications.
