We propose a positivity preserving entropy decreasing finite volume scheme for nonlinear nonlocal equations with a gradient flow structure. These properties allow for accurate computations of stationary states and long-time asymptotics demonstrated by suitably chosen test cases in which these features of the scheme are essential. The proposed scheme is able to cope with non-smooth stationary states, different time scales including metastability, as well as concentrations and self-similar behavior induced by singular nonlocal kernels. We use the scheme to explore properties of these equations beyond their present theoretical knowledge.

Motivated by a class of nonlinear nonlocal equations of interest for string theory, we introduce Sobolev spaces on arbitrary locally compact abelian groups and we examine some of their properties. Specifically, we focus on analogs of the Sobolev embedding and Rellich–Kondrachov compactness theorems. As an application, we prove the existence of continuous solutions to a generalized bosonic string equation posed on an arbitrary compact abelian group, and we also remark that our approach allows us to solve very general linear equations in a 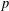$p$-adic context.