We show that if M is a countable transitive model of $\text {ZF}$ and if $a,b$ are reals not in M, then there is a G generic over M such that $b \in L[a,G]$ . We then present several applications such as the following: if J is any countable transitive model of $\text {ZFC}$ and $M \not \subseteq J$ is another countable transitive model of $\text {ZFC}$ of the same ordinal height $\alpha $ , then there is a forcing extension N of J such that $M \cup N$ is not included in any transitive model of $\text {ZFC}$ of height $\alpha $ . Also, assuming $0^{\#}$ exists, letting S be the set of reals generic over L, although S is disjoint from the Turing cone above $0^{\#}$ , we have that for any non-constructible real a, $\{ a \oplus s : s \in S \}$ is cofinal in the Turing degrees.

We analyze the precise modal commitments of several natural varieties of set-theoretic potentialism, using tools we develop for a general model-theoretic account of potentialism, building on those of Hamkins, Leibman and Löwe [14], including the use of buttons, switches, dials and ratchets. Among the potentialist conceptions we consider are: rank potenti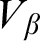alism (true in all larger $V_\beta $ ), Grothendieck–Zermelo potentialism (true in all larger 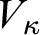$V_\kappa $ for inaccessible cardinals 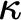$\kappa $ ), transitive-set potentialism (true in all larger transitive sets), forcing potentialism (true in all forcing extensions), countable-transitive-model potentialism (true in all larger countable transitive models of ZFC), countable-model potentialism (true in all larger countable models of ZFC), and others. In each case, we identify lower bounds for the modal validities, which are generally either S4.2 or S4.3, and an upper bound of S5, proving in each case that these bounds are optimal. The validity of S5 in a world is a potentialist maximality principle, an interesting set-theoretic principle of its own. The results can be viewed as providing an analysis of the modal commitments of the various set-theoretic multiverse conceptions corresponding to each potentialist account.

We prove that the determinacy of Gale-Stewart games whose winning sets are accepted by realtime 1-counter Büchi automata is equivalent to the determinacy of (effective) analytic Gale-Stewart games which is known to be a large cardinal assumption. We show also that the determinacy of Wadge games between two players in charge of ω-languages accepted by 1-counter Büchi automata is equivalent to the (effective) analytic Wadge determinacy. 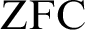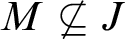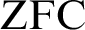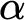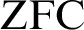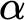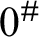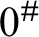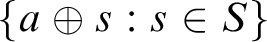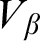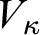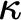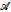Using some results of set theory we prove that one can effectively construct a 1-counter Büchi automaton and a Büchi automaton 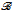such that: (1) There exists a model of ZFC in which Player 2 has a winning strategy in the Wadge game W(L(), L()); (2) There exists a model of ZFC in which the Wadge game W(L(), L()) is not determined. Moreover these are the only two possibilities, i.e. there are no models of ZFC in which Player 1 has a winning strategy in the Wadge game W(L(), L()).

We prove that some fairly basic questions on automata reading infinite words depend on the models of the axiomatic system ZFC. It is known that there are only three possibilities for the cardinality of the complement of an ω-language \hbox{$L(\mathcal{A})$}L(𝒜) accepted by a Büchi 1-counter automaton \hbox{$\mathcal{A}$}𝒜. We prove the following surprising result: there exists a 1-counter Büchi automaton \hbox{$\mathcal{A}$}𝒜 such that the cardinality of the complement \hbox{$L(\mathcal{A})^-$}L(𝒜) −  of the ω-language \hbox{$L(\mathcal{A})$}L(𝒜) is not determined by ZFC: (1) There is a model V1 of ZFC in which \hbox{$L(\mathcal{A})^-$}L(𝒜) −  is countable. (2) There is a model V2 of ZFC in which \hbox{$L(\mathcal{A})^-$}L(𝒜) −  has cardinal 2ℵ0. (3) There is a model V3 of ZFC in which \hbox{$L(\mathcal{A})^-$}L(𝒜) −  has cardinal ℵ1 with ℵ0 < ℵ1 < 2ℵ0.

We prove a very similar result for the complement of an infinitary rational relation accepted by a 2-tape Büchi automaton ℬ. As a corollary, this proves that the continuum hypothesis may be not satisfied for complements of 1-counter ω-languages and for complements of infinitary rational relations accepted by 2-tape Büchi automata. We infer from the proof of the above results that basic decision problems about 1-counter ω-languages or infinitary rational relations are actually located at the third level of the analytical hierarchy. In particular, the problem to determine whether the complement of a 1-counter ω-language (respectively, infinitary rational relation) is countable is in Σ13\(Π12 ∪ Σ12). This is rather surprising if compared to the fact that it is decidable whether an infinitary rational relation is countable (respectively, uncountable).