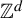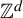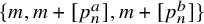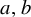We show that, under finitely many ergodicity assumptions, any multicorrelation sequence defined by invertible measure-preserving $\mathbb {Z}^d$-actions with multivariable integer polynomial iterates is the sum of a nilsequence and a nullsequence, extending a recent result of the second author. To this end, we develop a new seminorm bound estimate for multiple averages by improving the results in a previous work of the first, third, and fourth authors. We also use this approach to obtain new criteria for joint ergodicity of multiple averages with multivariable polynomial iterates on ${\mathbb Z}^{d}$-systems.

We examine multiple ergodic averages of commuting transformations with polynomial iterates in which the polynomials may be pairwise dependent. In particular, we show that such averages are controlled by the Gowers–Host–Kra seminorms whenever the system satisfies some mild ergodicity assumptions. Combining this result with the general criteria for joint ergodicity established in our earlier work, we determine a necessary and sufficient condition under which such averages are jointly ergodic, in the sense that they converge in the mean to the product of integrals, or weakly jointly ergodic, in that they converge to the product of conditional expectations. As a corollary, we deduce a special case of a conjecture by Donoso, Koutsogiannis, and Sun in a stronger form.

We establish the mean convergence for multiple ergodic averages with iterates given by distinct fractional powers of primes and related multiple recurrence results. A consequence of our main result is that every set of integers with positive upper density contains patterns of the form $\{m,m+[p_n^a], m+[p_n^b]\}$ , where $a,b$ are positive nonintegers and $p_n$ denotes the nth prime, a property that fails if a or b is a natural number. Our approach is based on a recent criterion for joint ergodicity of collections of sequences, and the bulk of the proof is devoted to obtaining good seminorm estimates for the related multiple ergodic averages. The input needed from number theory are upper bounds for the number of prime k-tuples that follow from elementary sieve theory estimates and equidistribution results of fractional powers of primes in the circle.