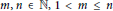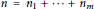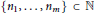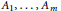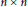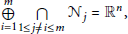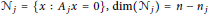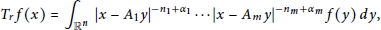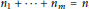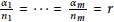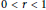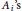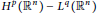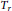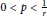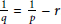For 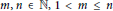$m,n\,\in \,\mathbb{N},\,1\,<\,m\le \,n$, we write 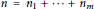$n={{n}_{1}}+\cdots +{{n}_{m}}$ where 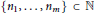$\{{{n}_{1}},\ldots \,,{{n}_{m}}\}\,\subset \,\mathbb{N}$. Let 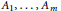${{A}_{1}}\,,\,\ldots \,,\,{{A}_{m}}$ be 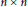$n\,\times \,n$ singular real matrices such that

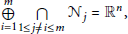$$\underset{i=1\,}{\overset{m}{\mathop{\oplus }}}\,\underset{1\le j\ne i\le m}{\mathop \bigcap }\,\,{{N}_{j}}\,=\,{{\mathbb{R}}^{n}},$$

where 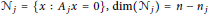${{N}_{j}}\,=\,\{x\,:\,{{A}_{j}}x\,=\,0\},\,\text{dim(}{{N}_{j}}\text{)}\,=\,n\,-\,{{n}_{j}}$, and 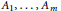${{A}_{1}}\,,\,\ldots \,,\,{{A}_{m}}$ is invertible. In this paper we study integral operators of the form

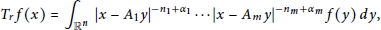$${{T}_{r}}f(x)\,=\,{{\int }_{{{\mathbb{R}}^{n}}}}|x\,-\,{{A}_{1y}}{{|}^{-{{n}_{1}}+{{\alpha }_{{{1}_{\ldots }}}}}}|x\,-\,{{A}_{m}}y{{|}^{-{{n}_{m}}+{{\alpha }_{m}}}}f(y)dy,$$

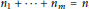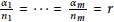${{n}_{1}}\,+\,\cdots \,+\,{{n}_{m}}\,=\,n$ , $\frac{{{\alpha }_{1}}}{{{n}_{1}}}\,=\,\cdots \,=\,\frac{{{\alpha }_{m}}}{{{n}_{m}}}\,=\,r$, 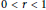$0\,<\,r\,<\,1$, and the matrices 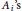${{A}_{i}}\text{ }\!\!'\!\!\text{ s}$ are as above. We obtain the 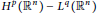${{H}^{p}}({{\mathbb{R}}^{n}})\,-\,{{L}^{q}}({{\mathbb{R}}^{n}})$ boundedness of 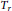${{T}_{r}}$ for 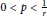$0\,<\,p\,<\,\frac{1}{r}$ and 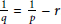$\frac{1}{q}\,=\,\frac{1}{p}\,-\,r$.

We give a partial answer to a conjecture of Dostanić on the determination of the norm of a class of integral operators induced by the weighted Bergman projection in the upper half plane.

We give a characterization of pairs of weights for the validity of weighted inequalities involving certain generalized geometric mean operators generated by some Volterra integral operators, which include the Hardy averaging operator and the Riemann–Liouville integral operators. The estimations of the constants are also discussed. Our results generalize the work done by J. A. Cochran, C.-S. Lee, H. P. Heinig, B. Opic, P. Gurka, and L. Pick.

Inspired by a statement of W. Luh asserting the existence of entire functions having together with all their derivatives and antiderivatives some kind of additive universality or multiplicative universality on certain compact subsets of the complex plane or of, respectively, the punctured complex plane, we introduce in this paper the new concept of U-operators, which are defined on the space of entire functions. Concrete examples, including differential and antidifferential operators, composition, multiplication and shift operators, are studied. A result due to Luh, Martirosian and Müller about the existence of universal entire functions with gap power series is also strengthened.