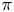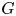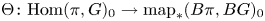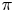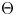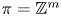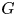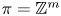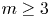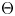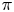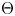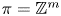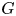Let $\pi$ be a discrete group, and let $G$ be a compact-connected Lie group. Then, there is a map $\Theta \colon \mathrm {Hom}(\pi,G)_0\to \mathrm {map}_*(B\pi,BG)_0$ between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for $\pi$ a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map $\Theta$ is surjective in rational cohomology for $\pi =\mathbb {Z}^m$ and the classical group $G$ except for $SO(2n)$, and that it is not surjective for $\pi =\mathbb {Z}^m$ with $m\ge 3$ and $G=SO(2n)$ with $n\ge 4$. As an application, we consider the surjectivity of the map $\Theta$ in rational cohomology for $\pi$ a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map $\Theta$ in rational homotopy groups for $\pi =\mathbb {Z}^m$ and the classical groups $G$ except for $SO(2n)$.

Fix a $\tau$-connection DL on a line bundle L over $X\times \mathbb{C}$, where X is a compact connected Riemann surface of genus at least three. Let $\mathcal{M}_X(D_L)$ denote the moduli space of all semistable $\tau$-connections of rank n, where $n\geq 2$, with the property that the induced $\tau$-connection on the top exterior product is isomorphic to (L, DL). Let $\mathcal{M}_Y(D_M)$ be the similar moduli space for another Riemann surface Y with genus(Y) = genus(X), where DM is a $\tau$-connection on a line bundle M over $Y\times \mathbb{C}$. We prove that if the variety $\mathcal{M}_X(D_L)$ is isomorphic to $\mathcal{M}_Y(D_M)$, then X is isomorphic to Y.

Let $\mathcal{M}^D_X$ denote the moduli space of all rank n flat connections on X. We prove that $\mathcal{M}^D_X$ determines X up to finitely many Riemann surfaces. For the very general Riemann surface X, the variety $\mathcal{M}^D_X$ determines X.