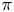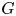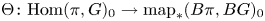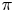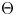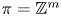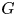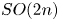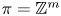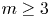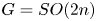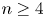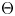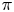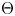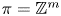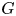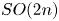1. Introduction
Given two topological groups $G$
and $H$
, there is a natural map
sending a homomorphism to its induced map between classifying spaces, where $\mathrm {Hom}(G,H)$
and $\mathrm {map}_*(BG,BH)$
denote the spaces of homomorphisms and based maps, respectively. If $G$
and $H$
are discrete, then the map $\widehat {\Theta }$
in $\pi _0$
is a well-known bijection:
However, the map $\widehat {\Theta }$
in $\pi _0$
is not bijective in general. Indeed, if $G=H=U(n)$
, then Sullivan [Reference Sullivan28] constructed a map between classifying spaces, called the unstable Adams operation, which is not in the image of the map $\widehat {\Theta }$
in $\pi _0$
, even rationally. Since then, the map $\widehat {\Theta }$
in $\pi _0$
has been intensely studied for both $G$
and $H$
being Lie groups completed at a prime, which led to a new development of algebraic topology and has been producing a variety of applications. See surveys [Reference Broto, Levi and Oliver11, Reference Grodal17, Reference Jackowski, McClure and Oliver20] for details. Clearly, the map $\widehat {\Theta }$
is of particular importance not only in $\pi _0$
. However, not much is known about higher homotopical structures of the map $\widehat {\Theta }$
such as homotopy groups and (co)homology of dimension $\ge 1$
.
We describe two interpretations of the map $\widehat {\Theta }$
. The first one is from algebraic topology. Stasheff [Reference Stasheff27] introduced an $A_\infty$
-map between topological monoids, which is defined by replacing the equality in the definition of a homomorphism by coherent higher homotopies with respect to the associativity of the multiplications. He also showed that to each $A_\infty$
-map, we can assign a map between classifying spaces, and so there is a map
where $\mathcal {A}_\infty (G,H)$
denotes the space of $A_\infty$
-maps between topological groups $G,H$
. It is proved in [Reference Fuchs14, Reference Tsutaya29] that this map is a weak homotopy equivalence, and since the map $\widehat {\Theta }$
factors through this map, we can interpret that the map $\widehat {\Theta }$
depicts the difference of homomorphisms, solid objects, and $A_\infty$
-maps, soft objects, between topological groups.
The second interpretation is from bundle theory. Let $\pi$
be a finitely generated discrete group, and let $G$
be a compact-connected Lie group. Let $\mathrm {Hom}(\pi,G)_0$
and $\mathrm {map}_*(B\pi,BG)_0$
denote the path components of $\mathrm {Hom}(\pi,G)$
and $\mathrm {map}_*(B\pi,BG)$
containing trivial maps, respectively. In this paper, we study the natural map
which is the restriction of the map $\widehat {\Theta }$
. If $B\pi$
has the homotopy type of a manifold $M$
, then $\mathrm {Hom}(\pi,G)_0$
and $\mathrm {map}_*(B\pi,BG)_0$
are identified with the based moduli spaces of flat connections and all connections on the trivial $G$
-bundle over $M$
, denoted by $\mathrm {Flat}(M,G)_0$
and $\mathcal {C}(M,G)_0$
, respectively. Under this identification, the map $\Theta$
can be interpreted as the inclusion:
Atiyah and Bott [Reference Atiyah and Bott4] studied the map $\Theta$
for a surface group $\pi$
through the above flat bundle interpretation in the context of gauge theory because flat connections are solutions to the Yang–Mills equation over a Riemann surface. In particular, they used Morse theory to prove that the map $\Theta$
is surjective in rational cohomology whenever $\pi$
is a surface group. However, their proof is so specialized to surface groups that it does not apply to other groups $\pi$
. Then, we ask:
Question 1.1 Is the map $\Theta$
surjective in rational cohomology whenever $B\pi$
is of the homotopy type of a manifold?
In this paper, we study the above question in the special case $\pi =\mathbb {Z}^m$
. The space $\mathrm {Hom}(\mathbb {Z}^m,G)$
is called the space of commuting elements in $G$
because there is a natural homeomorphism
where we will not distinguish these two spaces. Recently, several results on the space of commuting elements in a Lie group have been obtained from a view of algebraic topology [Reference Adem and Cohen1–Reference Adem, Gómez and Gritschacher3, Reference Baird5–Reference Baird and Ramras7, Reference Crabb12, Reference Goldman15, Reference Gómez, Pettet and Souto16, Reference Kishimoto and Takeda21, Reference Kishimoto and Takeda22, Reference Ramras and Stafa25, Reference Ramras and Stafa26]. In particular, the first and the second authors gave a minimal generating set of the rational cohomology of $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
when $G$
is the classical group except for $SO(2n)$
. Using this generating set, we will prove:
Theorem 1.2 If $G$
is the classical group except for $SO(2n)$
, then the map
is surjective in rational cohomology.
As an application of theorem 1.2, we will prove the following theorem. We refer to [Reference Hilton, Mislin and Roitberg19] for the localization of nilpotent groups.
Theorem 1.3 Let $\pi$
be a finitely generated nilpotent group, and let $G$
be the classical group except for $U(1)$
and $SO(2n)$
. Then, the map
is surjective in rational cohomology if and only if the rationalization $\pi _{(0)}$
is abelian.
As a corollary, we will obtain:
Corollary 1.4 Let $M$
be a nilmanifold, and let $G$
be the classical group except for $SO(2n)$
. Then, the inclusion
is surjective in rational cohomology if and only if $M$
is a torus.
As a corollary to theorem 1.2, we will show that the map $\Theta$
is surjective in rational cohomology for $G=SO(2n)$
with $n=2,3$
(corollary 3.10). On the contrary, as mentioned above, the result of Atiyah and Bott [Reference Atiyah and Bott4] implies that the map $\Theta$
is surjective in rational cohomology for $m=2$
and $G=SO(2n)$
with any $n\ge 2$
. Then, we may expect that the map $\Theta$
is also surjective in rational cohomology for $m\ge 3$
and $n\ge 4$
. However, the surjectivity breaks as:
Theorem 1.5 For $m\ge 3$
and $n\ge 4$
, the map
is not surjective in rational cohomology.
We will also consider the map $\Theta$
in rational homotopy groups. It is proved in [Reference Kishimoto and Takeda21] that $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
is rationally hyperbolic, and so the total dimension of its rational homotopy groups is infinite. On the contrary, we will see in § 4 that the rational homotopy group of $\mathrm {map}_*(B\mathbb {Z}^m,BG)_0$
is finite dimensional. Then, the map $\Theta$
for $\pi =\mathbb {Z}^m$
cannot be injective. On the contrary, we can consider the surjectivity of the map $\Theta$
in rational homotopy groups by looking at its cokernel. Baird and Ramras [Reference Baird and Ramras7] gave a lower bound for the dimension of the cokernel of the map $\Theta$
for $G=\mathrm {GL}_n(\mathbb {C})$
in rational homotopy groups. In particular, for $\pi =\mathbb {Z}^m$
, they proved that the dimension of the cokernel of the map
is bounded below by $\sum _{i< k\le n}\binom {m}{2i-k}$
whenever $n\ge {(m+i)}/{2}$
. By using theorem 1.2, we can improve this result as follows.
Theorem 1.6 Let $c_i(m,G)$
be the dimension of the cokernel of the map
(1) For $G=U(n),SU(n)$
, we have
\[ c_i(m,G)=\sum_{i< k\le n}\binom{m}{2i-k}. \]
(2) For $G=Sp(n),SO(2n+1)$
, we have
\[ c_i(m,G)\ge\sum_{{i}/{3}< k\le n}\binom{m}{4i-k} \]where the equality holds for $i\le 2n+3$
.
Remarks on theorem 1.6 are in order. By [Reference Gómez, Pettet and Souto16], $\pi _1(\mathrm {Hom}(\mathbb {Z}^m,G)_0)$
is abelian, and it is easy to see that $\pi _1(\mathrm {map}_*(B\mathbb {Z}^m,BG))$
is abelian too. Then, $\pi _1\otimes \mathbb {Q}$
in theorem 1.6 makes sense. By [Reference Bergeron8], the $G=U(n)$
case is equivalent to the $G=\mathrm {GL}_n(\mathbb {C})$
case, and so we can see that the lower bound of Baird and Ramras [Reference Baird and Ramras7] for $\pi =\mathbb {Z}^m$
mentioned above is attained by theorem 1.6.
2. The map $\Phi$
Hereafter, let $G$
be a compact-connected Lie group with maximal torus $T$
, and let $W$
denote the Weyl group of $G$
. We define a map
by $\Phi (gT,(g_1,\ldots,g_m))=(gg_1g^{-1},\ldots,gg_mg^{-1})$
for $g\in G$
and $g_1,\ldots,g_m\in T$
, where $T^m$
denotes the direct product of $m$
copies of $T$
, instead of a torus of dimension $m$
. In this section, we will define maps involving the map $\Phi$
and show their properties.
First, we recall the following result of Baird [Reference Baird5]. It is well known that there is a natural isomorphism:
and so we will not distinguish them. Baird [Reference Baird5] proved:
Theorem 2.1 The map
is an isomorphism.
By using theorem 2.1, the first and the second authors [Reference Kishimoto and Takeda21] gave a minimal generating set of the rational cohomology of $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
when $G$
is the classical group except for $SO(2n)$
, which we recall in the next section.
In order to define maps involving the map $\Phi$
, we need the functoriality of classifying spaces. Then, we employ the Milnor construction [Reference Milnor24] as a model for the classifying space. Let
where $X*Y$
denotes the join of spaces $X$
and $Y$
. Following Milnor [Reference Milnor24], we denote a point of $EG$
by
such that $t_i\ge 0$
, $\sum _{n\ge 1}t_n=1$
with only finitely many $t_i$
being non-zero, and $s_1g_1\oplus s_2g_2\oplus \cdots =t_1h_1\oplus t_2h_2\oplus \cdots$
if $s_k=t_k=0$
($g_k\ne h_k$
, possibly) and for $i\ne k$
, $s_i=t_i$
and $g_i=h_i$
, where $e$
denotes the identity element of $G$
. Then, $G$
acts freely on $EG$
by
We define the classifying space of $G$
by
Note that the inclusion $ET\to EG$
induces a map $\iota \colon BT\to EG/T$
which is a homotopy equivalence because both $ET$
and $EG$
are contractible. We record a simple fact which follows immediately from the definition of the Milnor construction.
Lemma 2.2 The natural map $BT\to BG$
factors as the composite:
Now, we define a map
for $g\in G$
and $[t_1g_1\oplus t_2g_2\oplus \cdots ]\in BT$
. Since $T$
is abelian, we have
for $h\in T$
, implying that the map $\phi$
is well-defined. We also define
Let $\alpha$
denote the composite $G/T\xrightarrow {\bar {\alpha }}EG/T\xrightarrow {\iota ^{-1}}BT$
. Then, there is a homotopy fibration $G/T\xrightarrow {\alpha }BT\to BG$
.
Lemma 2.3 There is a map $\widehat {\phi }\colon G/T\times BT\to BT$
satisfying the homotopy commutative diagram:
Proof. Define a map:
Quite similarly to the map $\phi$
, we can see that the map $\bar {\phi }$
is well-defined. Let $\widehat {\phi }$
denote the composite:
Then, by lemma 2.2, the right square of the diagram in the statement is homotopy commutative. We also have
and
for $[t_1g_1\oplus t_2g_2\oplus \cdots ]\in BT$
, where $[1e\oplus 0e\oplus 0e\oplus \cdots ]$
is the basepoint of $BT$
. Then, the left square is homotopy commutative too, finishing the proof.
We may think of the map $\widehat {\phi }$
as a higher version of the map defined by conjugation in [Reference Bott10]. We define a map
by $\widehat {\Phi }(gT,f)(x)=\phi (gT,f(x))$
for $g\in G,\,f\in \mathrm {map}_*(B\mathbb {Z}^m,BT)_0$
and $x\in B\mathbb {Z}^m$
. Since there is a natural homomorphism $\mathrm {Hom}(\mathbb {Z}^m,T)_0\cong T^m$
, we will not distinguish them.
Lemma 2.4 There is a commutative diagram:
Proof. By definition, we have
for $f\in \mathrm {Hom}(\mathbb {Z}^m,T)_0$
and $[t_1g_1\oplus t_2g_2\oplus \cdots ]\in B\mathbb {Z}^m$
. Then, we get
for $g\in G,\,f\in \mathrm {Hom}(\mathbb {Z}^m,T)_0$
and $[t_1g_1\oplus t_2g_2\oplus \cdots ]\in B\mathbb {Z}^m$
. Thus, the proof is finished.
Next, we consider the evaluation map:
Note that the map $\phi \colon G/T\times BT\to BG$
factors through $G/T\times _WBT$
. We denote the map $G/T\times _WBT\to BG$
by the same symbol $\phi$
.
Lemma 2.5 There is a commutative diagram:
Proof. For $g\in G$
, $f\in \mathrm {map}_*(B\mathbb {Z}^m,BT)_0$
and $x\in B\mathbb {Z}^m$
, we have
Thus, the statement is proved.
3. Rational cohomology
In this section, we will prove theorems 1.2 and 1.5, and we will apply theorem 1.2 to prove theorem 1.3. To prove theorem 1.2, we will employ the generating set of the rational cohomology of $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
given in [Reference Kishimoto and Takeda21], and to prove theorem 1.5, we will consider a specific element of $H^*(\mathrm {Hom}(\mathbb {Z}^m,SO(2n))_0)\cong H^*(SO(2n)/T\times T^m)^W$
.
3.1 Cohomology generators
Hereafter, the coefficients of (co)homology will be always in $\mathbb {Q}$
, and we will suppose that $G$
is of rank $n$
, unless otherwise specified. First, we set notation on cohomology. Since $G$
is of rank $n$
, the cohomology of $BT$
is given by
We also have that the cohomology of $T^m$
is given by
such that $y_i^k=\pi _k^*(\overset {k}{\sigma (x_i)})$
, where $\pi _k\colon B\mathbb {Z}^m\to B\mathbb {Z}$
is the $k$
-th projection and $\sigma$
denotes the cohomology suspension. Let $[m]=\{1,2,\ldots,m\}$
. For $I=\{i_1<\cdots < i_k\}\subset [m]$
, we set:
It is well known that the map $\alpha \colon G/T\to BT$
induces an isomorphism:
We denote $\alpha ^*(x_i)$
by the same symbol $x_i$
, and so $H^*(G/T)$
is generated by $x_1,\ldots,x_n$
.
Now, we recall the minimal generating set of the rational cohomology of $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
given in [Reference Kishimoto and Takeda21]. For $d\ge 1$
and $I\subset [m]$
, we define
and let
where we have $|z(d,I)|=2d+|I|-2$
. We also let:
where $x_1+\cdots +x_n=0$
and $y_1^i+\cdots +y_n^i=0$
for $i=1,\ldots,m$
. Since $W$
is the symmetric group on $[n]$
for $G=U(n),SU(n)$
such that for $\sigma \in W$
, $\sigma (x_i)=x_{\sigma (i)}$
and $\sigma (y_i^j)=y_{\sigma (i)}^j$
, we have
For an integer $k$
, let $\epsilon (k)=0$
for $k$
even and $\epsilon (k)=1$
for $k$
odd. We define
and let
where we have $|w(d,I)|=4d+|I|+2\epsilon (|I|)-4$
. We also let
Since $W$
is the signed symmetric group on $[n]$
for $G=Sp(n),SO(2n+1)$
such that for $\sigma \in W$
, $(\pm \sigma )(x_i)=\pm x_{\sigma (i)}$
and $(\pm \sigma )(y_i^j)=\pm y_{\sigma (i)}^j$
, we have
The following theorem is proved in [Reference Kishimoto and Takeda21].
Theorem 3.1 If $G$
is the classical group except for $SO(2n)$
, $(\Phi ^*)^{-1}(\mathcal {S}(m,G))$
is a minimal generating set of the rational cohomology of $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
.
3.2 Proof of theorem 1.2
First, we consider the map $\widehat {\phi }\colon G/T\times BT\to BT$
of lemma 2.3 in cohomology.
Lemma 3.2 For each $x_i\in H^*(BT)$
, we have
Proof. The statement immediately follows from the left square of the homotopy commutative diagram in lemma 2.3.
Next, we consider the map $\Theta \colon \mathrm {Hom}(\mathbb {Z}^m,T)_0\to \mathrm {map}_*(B\mathbb {Z}^m,BT)_0$
.
Lemma 3.3 The map $\Theta \colon \mathrm {Hom}(\mathbb {Z},T)_0\to \mathrm {map}_*(B\mathbb {Z},BT)_0$
is a homotopy equivalence.
Proof. For a topological group $K$
with a non-degenerate unit, there is a homomorphism $(K*K)/K\cong \widetilde {\Sigma }K$
such that the composite
is identified with the adjoint of the natural homotopy equivalence $K\simeq \Omega BK$
, where $\widetilde {\Sigma }$
denotes the unreduced suspension. By definition, $\widetilde {\Sigma }\mathbb {Z}$
is homotopy equivalent to a wedge of infinitely many copies of $S^1$
, and the map $\widetilde {\Sigma }\mathbb {Z}\to B\mathbb {Z}$
is identified with the fold map onto $S^1$
. Thus, the composite $\widetilde {\Sigma }\{0,1\}\to \widetilde {\Sigma }\mathbb {Z}\to B\mathbb {Z}$
is a homotopy equivalence. Note that for any homomorphism $f\colon \mathbb {Z}\to T$
, there is a commutative diagram:
Thus, since $\mathrm {Hom}(\mathbb {Z},T)_0=\mathrm {map}_*(\{0,1\},T)_0$
, we get a commutative diagram:
Clearly, the composite of the top maps is identified with the homotopy equivalence $\mathrm {map}_*(\{0,1\},\Omega BT)_0\cong \mathrm {map}_*(\Sigma \{0,1\},BT)_0$
. Then, the bottom map is a homotopy equivalence too, completing the proof.
Lemma 3.4 The map $\Theta \colon \mathrm {Hom}(\mathbb {Z}^m,T)_0\to \mathrm {map}_*(B\mathbb {Z}^m,BT)_0$
is a homotopy equivalence.
Proof. Let $F_m$
be the free group of rank $m$
. Clearly, we have
Since $BF_m$
is homotopy equivalent to a wedge of $m$
copies of $S^1$
, we also have
It is easy to see that through these equivalences, the map $\Theta \colon \mathrm {Hom}(F_m,T)_0\to \mathrm {map}_*(BF_m,BT)_0$
is identified with the product of $m$
copies of the map $\Theta \colon \mathrm {Hom}(\mathbb {Z},T)_0\to \mathrm {map}_*(B\mathbb {Z},BT)_0$
. Thus, by lemma 3.3, the map $\Theta \colon \mathrm {Hom}(F_m,T)_0\to \mathrm {map}_*(BF_m,BT)_0$
is a homotopy equivalence. Now, we consider the commutative diagram
induced from the abelianization $F_m\to \mathbb {Z}^m$
. Since $T$
is abelian, the left map is a homomorphism. Since the cofibre of the map $BF_m\to B\mathbb {Z}^m$
is simply-connected, the right map is a homotopy equivalence. Thus, the top map is a homotopy equivalence too, completing the proof.
We consider the evaluation map $\omega \colon \mathrm {map}_*(B\mathbb {Z}^m,BT)_0\times B\mathbb {Z}^m\to BT$
in cohomology. Since $B\mathbb {Z}^m$
is homotopy equivalent to the $m$
-dimensional torus, we have
For $I=\{i_1<\cdots < i_k\}\subset [m]$
, let:
Lemma 3.5 For each $x_i\in H^*(BT)$
, we have
Proof. For the evaluation map $\omega \colon \mathrm {map}_*(B\mathbb {Z},BT)_0\times B\mathbb {Z}\to BT$
, we have
as in [Reference Kishimoto and Kono23], where we identify $\mathrm {map}_*(B\mathbb {Z},BT)_0$
with $T$
. By lemma 3.4, we may assume $\Theta ^*(y_1^1)=y_1^1$
. Let $\iota _i\colon B\mathbb {Z}\to B\mathbb {Z}^m$
and $\pi _i\colon B\mathbb {Z}^m\to B\mathbb {Z}$
denote the $i$
-th inclusion and the $i$
-th projection, respectively. Since $\omega \circ (\pi _i^*\times \iota _j)$
is trivial for $i\ne j$
, $\omega ^*(x_k)$
is a linear combination of $\pi _k^*(y_1^1)\times t_1,\ldots,\pi _k^*(y_1^m)\times t_m$
. There is a commutative diagram:
Then, we get:
Thus, the proof is finished.
Next, we consider the evaluation map $\omega \colon \mathrm {map}_*(B\mathbb {Z}^m,BG)_0\times B\mathbb {Z}^m\to BG$
in cohomology. Recall that the rational cohomology of $BG$
is given by
We choose generators $z_1,\ldots,z_n$
as
and set $H^*(BSU(n))=H^*(BU(n))/(z_1)$
, where $j\colon BT\to BG$
denotes the natural map. For $i=1,\ldots,n$
and $\emptyset \ne I\subset [m]$
, we define $z_{i,I}\in H^*(\mathrm {map}_*(B\mathbb {Z}^m,BG)_0)$
by
where $z_{i,I}=1$
for $|z_i|=|I|$
and $z_{i,I}=0$
for $|z_i|<|I|$
.
Proposition 3.6 The rational cohomology of $\mathrm {map}_*(B\mathbb {Z}^m,BG)_0$
is a free commutative-graded algebra generated by
Proof. Since the rationalization of $BG$
is homotopy equivalent to a product of Eilenberg–MacLane spaces, so is the rationalization of $\mathrm {map}_*(B\mathbb {Z}^m,BG)_0$
. Then, the cohomology of $\mathrm {map}_*(B\mathbb {Z}^m,BG)_0$
is a free commutative algebra. The rest can be proved quite similarly to [Reference Atiyah and Bott4, Proposition 2.20].
We compute $\Theta ^*(z_{i,I})$
for the classical group $G$
except for $SO(2n)$
.
Proposition 3.7 For $i=1,\ldots,n$
and $\emptyset \ne I\subset [m]$
, if $|z_i|>|I|$
, then
Proof. First, we prove the $G=U(n)$
case. By lemmas 2.3 and 3.2, we have
By lemmas 2.4 and 2.5, there is a homotopy commutative diagram:
Then, by lemma 3.5, we get
Thus, the $G=U(n)$
case is proved. The $G=SU(n)$
case follows immediately from the $G=U(n)$
case, and the $G=Sp(n),SO(2n+1)$
case can be proved verbatim.
Now, we are ready to prove theorem 1.2.
3.3 Proof of theorem 1.3
We show a property of the rational cohomology of a nilpotent group that we are going to use. We refer to [Reference Hilton, Mislin and Roitberg19] for the localization of nilpotent groups. For a finitely generated group $\pi$
, let $\overline {\mathrm {ab}}\colon \pi \to \mathbb {Z}^m$
denote the composite of the abelianization $\pi \to \pi ^\mathrm {ab}$
and the projection $\pi ^\mathrm {ab}\to \pi ^\mathrm {ab}/\mathrm {Tor}\cong \mathbb {Z}^m$
, where $\mathrm {Tor}$
is the torsion part of $\pi ^\mathrm {ab}$
.
Lemma 3.8 Let $\pi$
be a finitely generated nilpotent group. Then, the rationalization $\pi _{(0)}$
is abelian if and only if the map
is injective.
Proof. By definition, the rationalization of $B\pi$
is rationally homotopy equivalent to an iterated principal $S^1$
-bundles. Then, as in [Reference Hasegawa18], the minimal model of $B\pi$
is given by $(\Lambda (x_1,\ldots,x_n),d)$
for $|x_i|=1$
such that
Moreover, the minimal model of $B\mathbb {Z}^m$
is given by $(\Lambda (x_1,\ldots,x_m), d=0)$
such that the map $\overline {\mathrm {ab}}\colon B\pi \to B\mathbb {Z}^m$
induces the inclusion $(\Lambda (x_1,\ldots,x_m),d=0)\to (\Lambda (x_1,\ldots,x_n),d)$
. Observe that $\pi _{(0)}$
is abelian if and only if the map $\overline {\mathrm {ab}}\colon B\pi \to B\mathbb {Z}^m$
is a rational homotopy equivalence. Then, $\pi _{(0)}$
is abelian if and only if $m=n$
, which is equivalent to the map $\overline {\mathrm {ab}}^*\colon H^2(B\mathbb {Z}^m)\to H^2(B\pi )$
is injective.
Now, we are ready to prove theorem 1.3.
Proof of theorem 1.3. By the naturality of the map $\Theta$
, there is a commutative diagram:
Bergeron and Silberman [Reference Bergeron and Silberman9] proved that the left map is a homotopy equivalence. Since the rationalization of $BG$
is a product of Eilenberg–MacLane spaces, there is a rational homotopy equivalence
for any connected CW complex $X$
, which is natural with respect to $X$
and $G$
. In particular, since $\pi _4(BG)\cong \mathbb {Z}$
, there is a monomorphism $\iota \colon H_2(X)\to QH^2(\mathrm {map}_*(X,BG)_0)$
which is natural with respect to $X$
, where $QA$
denotes the module of indecomposables of an augmented algebra $A$
. Then, there is a commutative diagram:
By theorem 3.1 and propositions 3.6 and 3.7, the composite of the bottom maps is an isomorphism. Thus, by lemma 3.8, the statement is proved.
Proof of corollary 1.4. It is well known that a nilmanifold $M$
is homotopy equivalent to the classifying space of a finitely generated torsion-free nilpotent group. Thus, by theorem 1.3, the proof is finished.
3.4 Proof of theorem 1.5
Before we begin the proof of theorem 1.5, we consider the case of $SO(2n)$
for $n=2,3$
. We need the following lemma.
Lemma 3.9 Let $G,H$
be compact-connected Lie groups. If there is a covering $G\to H$
, then there is a commutative diagram:
where the vertical maps are isomorphisms in rational cohomology and rational homotopy groups.
Proof. Let $K$
be the fibre of the covering $G\to H$
. Then, $K$
is a finite subgroup of $G$
contained in the centre. In particular, the map $BG\to BH$
is a rational homotopy equivalence, implying that the right map is a rational homotopy equivalence. As is shown in [Reference Goldman15], the left map is a covering map with fibre $K^m$
, so it is an isomorphism in rational homotopy groups because the fundamental groups of $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
and $\mathrm {Hom}(\mathbb {Z}^m,H)_0$
are abelian as in [Reference Gómez, Pettet and Souto16]. It is also proved in [Reference Kishimoto and Takeda21] that the left map is an isomorphism in rational cohomology, completing the proof.
Corollary 3.10 For $n=2,3$
, the map
is surjective in rational cohomology.
Proof. By lemma 3.9, it is sufficient to prove the statement for $Spin(2n)$
, instead of $SO(2n)$
. Then, since $Spin(4)\cong SU(2)\times SU(2)$
and $Spin(6)\cong SU(4)$
, the proof is finished by theorem 1.2.
Now, we begin the proof of theorem 1.5. For a monomial $z=x_1^{i_1}\cdots x_n^{i_n}y_1^{I_1}\cdots y_n^{I_n}$
in $H^*(BT\times T^m)$
, let
where $I_1,\ldots,I_n\subset [m]$
. If all entries of $d(z)$
are even (resp. odd), then we call a monomial $z$
even (resp. odd).
Lemma 3.11 If $G=SO(2n)$
, then every element of $H^*(BT\times T^m)^W$
is a linear combination of even and odd monomials.
Proof. Given $1\le i< j\le n$
, there is $w\in W$
such that:
Then, every monomial $z$
in $H^*(BT\times T^m)$
satisfies $w(z)=(-1)^{{d}_i+{d}_j}z$
, where ${d}(z)=({d}_1,\ldots,{d}_n)$
. So if $z$
is contained in some element of $H^*(BT\times T^m)^W$
, ${d}_1+{d}_2,{d}_2+{d}_3,\ldots,{d}_{n-1}+{d}_n$
are even. Thus, $z$
is even for ${d}_1$
even, and $z$
is odd for ${d}_1$
odd, completing the proof.
We define a map
For $m\ge 3$
and $G=SO(2n)$
with $n\ge 4$
, let
and let $a=\pi (\bar {a})$
.
Lemma 3.12 The element $(\alpha \times 1)^*(a)$
of $H^*(SO(2n)/T\times T^m)^W$
is indecomposable, where $\alpha \colon G/T\rightarrow BT$
is as in § 2.
Proof. It is easy to see that $\alpha ^*(x_1\ldots x_{n-4})\ne 0$
in $H^*(SO(2n)/T)$
because
where $p_i$
is the $i$
-th elementary symmetric polynomial in $x_1^2,\ldots,x_n^2$
and $e=x_1\ldots x_n$
. Then, $(\alpha \times 1)^*(\bar {a})\ne 0$
in $H^*(SO(2n)/T\times T^m)$
. So, since $a$
includes the term $2^{n-1}(n-4)!\bar {a}$
, we have $(\alpha \times 1)^*(a)\ne 0$
in $H^*(SO(2n)/T\times T^m)^W$
.
Now, we suppose that $(\alpha \times 1)^*(a)$
is decomposable. Then, there are $b,c\in \widetilde {H}^*(BT\times T^m)$
such that $\pi (b)\pi (c)$
includes the monomial $\bar {a}$
, and so we may assume $\bar {a}=bc$
. Note that
Then, since ${d}(b)\ne 0$
and ${d}(c)\ne 0$
, it follows from lemma 3.11 that we may assume ${d}(b)=(1,\ldots,1)$
, implying $b=x_1\ldots x_{n-4}y_{n-3}^1y_{n-2}^2y_{n-1}^3y_n^i$
for some $i=1,2,3$
. Let $\sigma$
be the transposition of $n$
and $k$
, where $k=n-3,n-2,n-1$
for $i=1,2,3$
, respectively. Then, $\sigma$
belongs to $W$
, and $\sigma (b)=b$
. Let $W=V\sqcup V\sigma$
be the coset decomposition. Then, we have
and so we get $(\alpha \times 1)^*(a)=0$
, which is a contradiction. Thus, we obtain that $(\alpha \times 1)^*(a)$
is indecomposable, as stated.
Proposition 3.13 If $m\ge 3$
and $n\ge 4$
, then $(\alpha \times 1)^*(a)\in H^*(SO(2n)/T\times T^m)^W$
does not belong to the image of the composite
in rational cohomology.
Proof. First, we consider the $m=3$
case. Suppose that there is $\hat {a}\in H^*(\mathrm {map}_*(B\mathbb {Z}^3,BSO(2n))_0)$
such that $(\alpha \times 1)^*(a)=\Phi ^*(\Theta ^*(\hat {a}))$
. Then, by lemma 3.12, $\Phi ^*(\Theta ^*(\hat {a}))$
is indecomposable. On the contrary, by lemma 2.4, we have $\Phi ^*(\Theta ^*(\hat {a}))=\Theta ^*(\widehat {\Phi }^*(\hat {a}))=\widehat {\Phi }(\hat {a})$
, and by proposition 3.6, every indecomposable element of the image of $\widehat {\Phi }^*$
cannot contain a monomial $x_1^{i_1}\ldots x_n^{i_n}y_1^{I_1}\cdots y_n^{I_n}$
with $|I_1|+\cdots +|I_n|>4$
. Thus, we obtain a contradiction, so $(\alpha \times 1)^*(a)$
does not belong to the image of $\Phi ^*\circ \Theta ^*$
.
Next, we consider the case $m>3$
. Since $\mathbb {Z}^3$
is a direct summand of $\mathbb {Z}^m$
, the maps $\widehat {\Phi }$
and $\Theta$
for $m=3$
are homotopy retracts of the maps $\widehat {\Phi }$
and $\Theta$
for $m>3$
, respectively. Thus, the $m=3$
case above implies the $m>3$
case, completing the proof.
Now, we are ready to prove theorem 1.5.
4. Rational homotopy groups
This section proves theorem 1.6. We begin with a simple lemma. Let $\mathrm {hur}^*\colon H^*(X)\to \mathrm {Hom}(\pi _*(X),\mathbb {Q})$
denote the dual Hurewicz map. As in the proof of theorem 1.3, let $QA$
denote the module of indecomposables of an augmented algebra $A$
. We refer to [Reference Félix, Halperin and Thomas13] for rational homotopy theory.
Lemma 4.1 Let $X$
be a simply-connected space such that there is a map:
which is a rational equivalence in dimension $\le n$
, where $V_i$
is a $\mathbb {Q}$
-vector space of finite dimension. Then, for $i\le n+2$
, the map
is injective.
Proof. The minimal model of $X$
in dimension $\le n$
is given by
where $\Lambda V$
denotes the free commutative-graded algebra generated by a graded vector space $V$
and each $V_i$
is of degree $i$
. Then, there is no element of degree one in the minimal model of $X$
, so any element of $QH^i(X)$
for $i\le n+2$
is represented by an indecomposable element of the minimal model of $X$
. Since the module of indecomposables of the minimal model of $X$
is isomorphic to $\mathrm {Hom}(\pi _*(X),\mathbb {Q})$
through the dual Hurewicz map, the proof is finished.
We recall a property of the minimal generating set $\mathcal {S}(m,G)$
that we are going to use. Let:
Let $\mathbb {Q}\{S\}$
denote the graded $\mathbb {Q}$
-vector space generated by a graded set $S$
. We consider a map:
The following is proved in [Reference Kishimoto and Takeda21].
Theorem 4.2 Let $G$
be the classical group except for $SO(2n)$
. Then, the map
is an isomorphism in dimension $\le {d}(m,G)$
.
We define a map $\mathrm {hur}^*\colon \mathcal {S}(m,G)\to \mathrm {Hom}(\pi _*(\mathrm {Hom}(\mathbb {Z}^m,G)_0),\mathbb {Q})$
by the linear part of the map $\lambda$
in the minimal models.
Lemma 4.3 If $G$
is the classical group except for $SO(2n)$
, then the map
is injective in dimension $\le {d}(m,G)+2$
.
Proof. By [Reference Gómez, Pettet and Souto16], $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
is simply-connected whenever $G$
is simply-connected. Then, by lemma 3.9, we may assume $\mathrm {Hom}(\mathbb {Z}^m,G)_0$
is simply-connected for $G=SU(n),Sp(n),SO(2n+1)$
as long as we consider rational cohomology and rational homotopy groups. By theorem 4.2, the map $\lambda$
is an isomorphism in rational cohomology in dimension $\le {d}(m,G)$
. Then, the statement for $G=SU(n),Sp(n),SO(2n+1)$
is proved by the J.H.C. Whitehead theorem and lemma 4.1. For $G=U(n)$
, we may consider $S^1\times SU(n)$
by lemma 3.9, instead of $U(n)$
. In this case, the dual Hurewicz map for $G=U(n)$
is identified with the map:
because $\mathrm {Hom}(\mathbb {Z}^m,S^1\times SU(n))_0=(S^1)^m\times \mathrm {Hom}(\mathbb {Z}^m,SU(n))_0$
. Thus, the statement follows from the $G=SU(n)$
case.
Lemma 4.4 For $G=U(n),SU(n)$
, the map
is injective.
Proof. Let $G=U(n),SU(n)$
. We induct on $m$
. If $m=1$
, then the statement is obvious. Assume that the statement holds less than $m$
. Take any $\emptyset \ne I\subset [m]$
. Then, there are the obvious inclusion $\iota _I\colon \mathbb {Z}^{|I|}\to \mathbb {Z}^m$
and the obvious projection $\pi _I\colon \mathbb {Z}^m\to \mathbb {Z}^{|I|}$
such that $\pi _I\circ \iota _I=1$
. In particular, we get maps $\iota _I^*\colon \mathrm {Hom}(\mathbb {Z}^m,G)_0\to \mathrm {Hom}(\mathbb {Z}^{|I|},G)_0$
and $\pi _I^*\colon \mathrm {Hom}(\mathbb {Z}^{|I|},G)_0\to \mathrm {Hom}(\mathbb {Z}^m,G)_0$
such that $\iota _I^*\circ \pi _I^*=1$
. Note that the map $\pi _I^*$
induces a map $(\pi _I^*)^*\colon \mathcal {S}(m,G)\to \mathcal {S}(|I|,G)$
such that:
Then, there is a commutative diagram:
Now, we assume
for $a_{d,J}\in \mathbb {Q}$
. Then, by (4.1) and (
), we have
So, since the right map of (
4.2) is injective for $I\ne [m]$
by the induction hypothesis, we get $a_{d,J}=0$
for $J\ne [m]$
, implying:
Note that every $z(d,[m])\in \mathcal {S}(m,G)$
is of degree $\le 2n-m+1$
. Then, by lemma 4.3, we get $a_{d,[m]}=0$
, completing the proof.
Now, we prove theorem 1.6.
Proof of theorem 1.6. Let $\mathcal {S}_i$
and $\mathcal {S}_i(m,G)$
denote the degree $i$
parts of $\mathcal {S}$
and $\mathcal {S}(m,G)$
, respectively, where $\mathcal {S}$
is as in proposition 3.6. Then, by proposition 3.6 and theorem 4.2, there is a commutative diagram:
Let $K_i$
denote the kernel of the bottom map. Clearly, the dimension of $K_i$
coincides with
and so we compute $\dim K_i$
. By proposition 3.6, the left map is an isomorphism. Then, we get:
By lemma 4.3, the equality holds for $G=Sp(n),SO(2n+1)$
and $i\le d(m,G)+2$
, and by lemma 4.4, the equality holds for $G=U(n),SU(n)$
and all $i$
. We can easily compute:
and thus the proof is finished.
Acknowledgements
The authors were supported in part by JSPS KAKENHI JP17K05248 and JP19K03473 (Kishimoto), JP21J10117 (Takeda), and JP19K14535 (Tsutaya).
