We apply a mean-value inequality for positive subsolutions of the 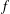 $f$-heat operator, obtained from a Sobolev embedding, to prove a nonexistence result concerning complete noncompact
$f$-heat operator, obtained from a Sobolev embedding, to prove a nonexistence result concerning complete noncompact 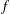 $f$-maximal spacelike hypersurfaces in a class of weighted Lorentzian manifolds. Furthermore, we establish a new Calabi–Bernstein result for complete noncompact maximal spacelike hypersurfaces in a Lorentzian product space.
$f$-maximal spacelike hypersurfaces in a class of weighted Lorentzian manifolds. Furthermore, we establish a new Calabi–Bernstein result for complete noncompact maximal spacelike hypersurfaces in a Lorentzian product space.
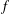 $f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS