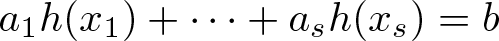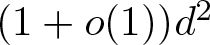1 results
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- HTML
- Export citation
-
We study density and partition properties of polynomial equations in prime variables. We consider equations of the form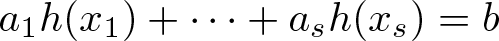
$a_1h(x_1) + \cdots + a_sh(x_s)=b$, where the ai and b are fixed coefficients and h is an arbitrary integer polynomial of degree d. We establish that the natural necessary conditions for this equation to have a monochromatic non-constant solution with respect to any finite colouring of the prime numbers are also sufficient when the equation has at least 
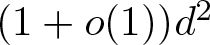$(1+o(1))d^2$ variables. We similarly characterize when such equations admit solutions over any set of primes with positive relative upper density. In both cases, we obtain lower bounds for the number of monochromatic or dense solutions in primes that are of the correct order of magnitude. Our main new ingredient is a uniform lower bound on the cardinality of a prime polynomial Bohr set.
