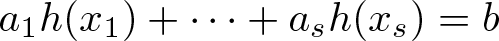1. Introduction
An influential theorem of Szemerédi asserts that sets of positive integers A with positive upper density, meaning that
 \begin{equation*}
\limsup_{N\to\infty}\frac{|A\cap\{1,2,\ldots,N\}|}{N} \gt 0,
\end{equation*}
\begin{equation*}
\limsup_{N\to\infty}\frac{|A\cap\{1,2,\ldots,N\}|}{N} \gt 0,
\end{equation*} must contain arbitrarily long arithmetic progressions. Green and Tao [Reference Green and Tao7] famously established a version of Szemerédi’s theorem for the primes. Specifically, writing ![]() $\mathcal P:=\{2,3,5,\ldots\}$ for the set of prime numbers, Green and Tao showed that sets
$\mathcal P:=\{2,3,5,\ldots\}$ for the set of prime numbers, Green and Tao showed that sets ![]() $A\subseteq\mathcal P$ satisfying
$A\subseteq\mathcal P$ satisfying
 \begin{equation}
\limsup_{N\to\infty}\frac{|A\cap\{1,2,\ldots,N\}|}{|\mathcal P\cap\{1,2,\ldots,N\}|} \gt 0
\end{equation}
\begin{equation}
\limsup_{N\to\infty}\frac{|A\cap\{1,2,\ldots,N\}|}{|\mathcal P\cap\{1,2,\ldots,N\}|} \gt 0
\end{equation}contain arbitrarily long arithmetic progressions. In particular, the primes themselves contain arithmetic progressions of any finite length.
One can consider configurations other than arithmetic progressions. We call a system of Diophantine equations density regular if it has non-constant solutions over all sets of positive integers with positive upper density. For example, consider a linear homogeneous equation
where ![]() $s\geqslant 3$ and
$s\geqslant 3$ and ![]() $a_1,\ldots,a_s$ are non-zero integers. Roth [Reference Roth20] showed that this equation is density regular if and only if
$a_1,\ldots,a_s$ are non-zero integers. Roth [Reference Roth20] showed that this equation is density regular if and only if ![]() $a_1+\cdots +a_s = 0$. Green [Reference Green6] subsequently proved that Roth’s theorem holds over the primes; Eq. (1.2) has non-constant solutions over any set of primes
$a_1+\cdots +a_s = 0$. Green [Reference Green6] subsequently proved that Roth’s theorem holds over the primes; Eq. (1.2) has non-constant solutions over any set of primes ![]() $A\subseteq\mathcal P$ satisfying (1.1) if and only if
$A\subseteq\mathcal P$ satisfying (1.1) if and only if ![]() $a_1+\cdots +a_s = 0$.
$a_1+\cdots +a_s = 0$.
A related, weaker notion of regularity is that of partition regularity, which refers to systems of Diophantine equations, which admit monochromatic non-constant solutions with respect to any finite colouring of the positive integers. By the pigeonhole principle, density regularity implies partition regularity. A foundational result in arithmetic Ramsey theory is Rado’s criterion [Reference Rado18, Satz IV], which completely characterizes partition regularity for finite systems of linear equations. In particular, Rado’s criterion reveals that Eq. (1.2) is partition regular if and only if there exists a non-empty set ![]() $I\subseteq\{1,\ldots,s\}$ such that
$I\subseteq\{1,\ldots,s\}$ such that ![]() $\sum_{i\in I}a_i = 0$.
$\sum_{i\in I}a_i = 0$.
Lê [Reference Lê11] observed that Green and Tao’s work provides a characterization of partition regularity for systems of linear homogeneous equations in shifted primes. For single equations, Lê proved that Eq. (1.2) admits monochromatic non-constant solutions with respect to any finite colouring of ![]() $\mathcal P+1:=\{p+1:p\in\mathcal P\}$ or
$\mathcal P+1:=\{p+1:p\in\mathcal P\}$ or ![]() $\mathcal P-1$ if and only if there exists a non-empty set
$\mathcal P-1$ if and only if there exists a non-empty set ![]() $I\subseteq\{1,\ldots,s\}$ such that
$I\subseteq\{1,\ldots,s\}$ such that ![]() $\sum_{i\in I}a_i = 0$. Note that there are divisibility obstructions that prevent such a result holding over the set
$\sum_{i\in I}a_i = 0$. Note that there are divisibility obstructions that prevent such a result holding over the set ![]() $\mathcal P+c$ for integers
$\mathcal P+c$ for integers ![]() $c\notin\{-1,1\}$. For example, the equation
$c\notin\{-1,1\}$. For example, the equation ![]() $x+y=z$ is partition regular, but if we partition
$x+y=z$ is partition regular, but if we partition ![]() $\mathcal P+c$ into residue classes modulo q for any prime q dividing c, then there are no monochromatic solutions to
$\mathcal P+c$ into residue classes modulo q for any prime q dividing c, then there are no monochromatic solutions to ![]() $x+y=z$.
$x+y=z$.
The purpose of this article is to obtain a complete classification of partition and density regularity over primes for equations in sufficiently many variables of the form
where ![]() $a_1,\ldots,a_s$ are non-zero integers, b is an integer, and h is a polynomial with integer coefficients. We say that (1.3) is partition regular over the primes if every finite colouring of the prime numbers produces a monochromatic non-constant solution to (1.3). Similarly, we call (1.3) density regular over the primes if (1.3) has a non-constant solution over any set of primes
$a_1,\ldots,a_s$ are non-zero integers, b is an integer, and h is a polynomial with integer coefficients. We say that (1.3) is partition regular over the primes if every finite colouring of the prime numbers produces a monochromatic non-constant solution to (1.3). Similarly, we call (1.3) density regular over the primes if (1.3) has a non-constant solution over any set of primes ![]() $A\subseteq\mathcal P$, which satisfies (1.1). For b = 0, observe that Lê’s result [Reference Lê11] asserts that Rado’s condition characterizes partition regularity over primes for (1.3) whenever
$A\subseteq\mathcal P$, which satisfies (1.1). For b = 0, observe that Lê’s result [Reference Lê11] asserts that Rado’s condition characterizes partition regularity over primes for (1.3) whenever ![]() $h(x)=x\pm 1$.
$h(x)=x\pm 1$.
In our previous work [Reference Chapman and Chow2], we established necessary and sufficient conditions for partition and density regularity (over ![]() $\mathbb{N}$) for all equations (1.3) in sufficiently many variables. We observed that it is necessary for partition regularity that h satisfies a certain ‘intersectivity condition’ in order to avoid divisibility obstructions, as alluded to above. For partition regularity over primes, we use the following definition, previously introduced in [Reference Lê12, Reference Rice19]. An integer polynomial h is intersective of the second kind if for each positive integer n, there exists an integer x which is coprime to n such that n divides h(x). Observe that any polynomial h satisfying
$\mathbb{N}$) for all equations (1.3) in sufficiently many variables. We observed that it is necessary for partition regularity that h satisfies a certain ‘intersectivity condition’ in order to avoid divisibility obstructions, as alluded to above. For partition regularity over primes, we use the following definition, previously introduced in [Reference Lê12, Reference Rice19]. An integer polynomial h is intersective of the second kind if for each positive integer n, there exists an integer x which is coprime to n such that n divides h(x). Observe that any polynomial h satisfying ![]() $h(1)=0$ or
$h(1)=0$ or ![]() $h(-1)=0$ is intersective of the second kind. However, one can construct numerous polynomials, such as
$h(-1)=0$ is intersective of the second kind. However, one can construct numerous polynomials, such as ![]() $(x^2 - 13)(x^2 - 17)(x^2 - 221)$ and
$(x^2 - 13)(x^2 - 17)(x^2 - 221)$ and ![]() $(x^3 - 19)(x^2 + x + 1)$, which are intersective of the second kind but do not have rational zeros (see [Reference Lê and Spencer13, §2]).
$(x^3 - 19)(x^2 + x + 1)$, which are intersective of the second kind but do not have rational zeros (see [Reference Lê and Spencer13, §2]).
Our main result is the following:
Theorem 1.1 Let ![]() $d\geqslant 2$ be an integer. There exists a positive integer
$d\geqslant 2$ be an integer. There exists a positive integer ![]() $s_0(d)$ such that the following is true. Let h be an integer polynomial of degree d, and let
$s_0(d)$ such that the following is true. Let h be an integer polynomial of degree d, and let ![]() $s\geqslant s_0(d)$ be an integer. Let
$s\geqslant s_0(d)$ be an integer. Let ![]() $a_1,\ldots,a_s$ be non-zero integers, and let b be an integer.
$a_1,\ldots,a_s$ be non-zero integers, and let b be an integer.
(PR) Equation (1.3) is partition regular over the primes if and only if there exists a non-empty set
 $I\subseteq\{1,\ldots,s\}$ with
$I\subseteq\{1,\ldots,s\}$ with  $\sum_{i\in I}a_i =0$ and an integer m with
$\sum_{i\in I}a_i =0$ and an integer m with  $b=(a_{1}+\cdots +a_s)m$ such that
$b=(a_{1}+\cdots +a_s)m$ such that  $h(x) - m$ is an intersective polynomial of the second kind.
$h(x) - m$ is an intersective polynomial of the second kind.(DR) Equation (1.3) is density regular over the primes if and only if
 $b=a_1 +\cdots +a_s = 0$.
$b=a_1 +\cdots +a_s = 0$.
Furthermore, we have ![]() $s_0(2)=5$,
$s_0(2)=5$, ![]() $s_0(3)\leqslant 9$, and
$s_0(3)\leqslant 9$, and
Remark 1.2. The integer ![]() $s_0(d)$, which is defined explicitly in §2, was previously introduced in [Reference Chapman and Chow2] to study partition and density regularity of equations (1.3).
$s_0(d)$, which is defined explicitly in §2, was previously introduced in [Reference Chapman and Chow2] to study partition and density regularity of equations (1.3).
Remark 1.3. The “only if” parts of both statements are true without any assumption on the number of variables s (see lemma 2.4). The above theorem asserts that these necessary conditions are sufficient provided ![]() $s\geqslant s_0(d)$.
$s\geqslant s_0(d)$.
Remark 1.4. The conditions in the partition regularity statement are trivially satisfied when ![]() $b=a_1+\cdots +a_s = 0$. Indeed, in this case, we can take
$b=a_1+\cdots +a_s = 0$. Indeed, in this case, we can take ![]() $I=\{1,\ldots,s\}$ and
$I=\{1,\ldots,s\}$ and ![]() $m=h(1)$. It then follows that
$m=h(1)$. It then follows that ![]() $h(x) - m$ vanishes at x = 1, whence
$h(x) - m$ vanishes at x = 1, whence ![]() $h(x)-m$ is trivially intersective of the second kind.
$h(x)-m$ is trivially intersective of the second kind.
In our previous work [Reference Chapman and Chow2], we obtained lower bounds for the number of solutions to (1.3) lying in dense or monochromatic subsets of the positive integers, which are sharp up to the leading constant. Our second main result is the following analogous counting version of theorem 1.1 for subsets of ![]() ${\mathcal P}_N:=\{p\leqslant N:p\;\text{prime}\}$.
${\mathcal P}_N:=\{p\leqslant N:p\;\text{prime}\}$.
Theorem 1.5 Let ![]() $d\geqslant 2$ be an integer, and let
$d\geqslant 2$ be an integer, and let ![]() $s_0(d)$ be as given in theorem 1.1. Let h be an integer polynomial of degree d. Let
$s_0(d)$ be as given in theorem 1.1. Let h be an integer polynomial of degree d. Let ![]() $s\geqslant s_0(d)$ be an integer. Let
$s\geqslant s_0(d)$ be an integer. Let ![]() $a_1,\ldots,a_s$ be non-zero integers, and let b be an integer. Given a set of integers
$a_1,\ldots,a_s$ be non-zero integers, and let b be an integer. Given a set of integers ![]() $\mathcal A$, write
$\mathcal A$, write
(PR) Suppose there exists a non-empty set
 $I\subseteq\{1,\ldots,s\}$ with
$I\subseteq\{1,\ldots,s\}$ with  $\sum_{i\in I}a_i =0$ and an integer m with
$\sum_{i\in I}a_i =0$ and an integer m with  $b=(a_{1}+\cdots +a_s)m$ such that
$b=(a_{1}+\cdots +a_s)m$ such that  $h(x) - m$ is an intersective polynomial of the second kind. Then, for any positive integer r, there exists a positive real number
$h(x) - m$ is an intersective polynomial of the second kind. Then, for any positive integer r, there exists a positive real number  $c_1 = c_1(h;a_1,\ldots,a_s,b;r)$ and a positive integer
$c_1 = c_1(h;a_1,\ldots,a_s,b;r)$ and a positive integer  $N_1 = N_1(h;a_1,\ldots,a_s,b;r)$ such that the following is true for any positive integer
$N_1 = N_1(h;a_1,\ldots,a_s,b;r)$ such that the following is true for any positive integer  $N\geqslant N_1$. Given any r-colouring
$N\geqslant N_1$. Given any r-colouring  $\mathcal P_N = \mathcal C_1 \cup\cdots\cup \mathcal C_r$, there exists
$\mathcal P_N = \mathcal C_1 \cup\cdots\cup \mathcal C_r$, there exists  $k\in\{1,\ldots,r\}$ such that
$k\in\{1,\ldots,r\}$ such that  $|S(\mathcal C_k)|\geqslant c_1N^{-d}(N/\log N)^{s}$.
$|S(\mathcal C_k)|\geqslant c_1N^{-d}(N/\log N)^{s}$.(DR) If
 $a_1 +\cdots +a_s = b = 0$, then for any positive real number δ > 0, there exists a positive real number
$a_1 +\cdots +a_s = b = 0$, then for any positive real number δ > 0, there exists a positive real number  $c_2= c_2(h;a_1,\ldots,a_s;\delta)$ and a positive integer
$c_2= c_2(h;a_1,\ldots,a_s;\delta)$ and a positive integer  $N_2 = N_2(h;a_1,\ldots,a_s;\delta)$ such that the following is true for any positive integer
$N_2 = N_2(h;a_1,\ldots,a_s;\delta)$ such that the following is true for any positive integer  $N\geqslant N_2$. Given any set
$N\geqslant N_2$. Given any set  $A\subseteq\mathcal P_N$ satisfying
$A\subseteq\mathcal P_N$ satisfying  $|A|\geqslant\delta |\mathcal P_N|$, we have
$|A|\geqslant\delta |\mathcal P_N|$, we have  $|S(A)|\geqslant c_2N^{-d}(N/\log N)^{s}$.
$|S(A)|\geqslant c_2N^{-d}(N/\log N)^{s}$.
1.1. Methods
Ourgoal is to find many monochromatic/dense solutions to
for some linear forms L 1 and L 2, where ![]() $L_1(1,\ldots,1) = 0$. Here, we have used the slight abuse of notation
$L_1(1,\ldots,1) = 0$. Here, we have used the slight abuse of notation ![]() $h(\mathbf{x})=(h(x_1),\ldots,h(x_s))$. In Fourier space, after normalization and accounting for small prime moduli (the W-trick), the image of h can be shown to behave like
$h(\mathbf{x})=(h(x_1),\ldots,h(x_s))$. In Fourier space, after normalization and accounting for small prime moduli (the W-trick), the image of h can be shown to behave like ![]() $\mathbb{N}$ for our count. The upshot is that it suffices to count solutions to an equation
$\mathbb{N}$ for our count. The upshot is that it suffices to count solutions to an equation
where hD is a related polynomial that is intersective of the second kind. This Fourier-analytic transference principle was introduced by Green [Reference Green6] to show that relatively dense sets of primes contain three-term arithmetic progressions and is based on Fourier decay and restriction (from harmonic analysis). The transference argument is sketched in further detail in the next section and formalized in the five sections afterwards. It can be regarded as a version of the Hardy–Littlewood circle method and estimates for prime Weyl sums feature prominently in our work.
To count monochromatic/dense solutions to our linearized equation, we use an arithmetic regularity lemma. This enables us to decompose the indicator functions of our colour classes into three parts, the first of which exhibits quasi-periodic structure and ultimately dominates the count. Using this quasi-periodicity to obtain a large count requires us to show that polynomials evaluated at primes are dense in Bohr sets, in a suitably uniform sense. The colour class that we choose maximizes this density.
Our main novelty is to uniformly bound from below the density of a ‘prime polynomial Bohr set’. This is accomplished by induction on the dimension, beginning with a result of Harman [Reference Harman8] from Diophantine approximation. The latter brings prime Weyl sums into play. The requisite data for these come partly from the analysis in the earlier sections, partly from Lucier’s pioneering work on intersective polynomials [Reference Lucier15], and partly from the investigations of Lê–Spencer [Reference Lê and Spencer14] and Rice [Reference Rice19] into polynomials that are intersective of the second kind.
1.2. Organization
We begin in §2 with some preliminary results. We prove the ‘only if’ parts of theorem 1.1 by establishing necessary conditions for (1.3) to be partition or density regular over the primes. We synthesize both the density and partition statements presented in theorem 1.5 into a single result, theorem 2.6, on counting solutions to certain linear form equations. We also recall the ‘auxiliary intersective polynomials’ of Lucier [Reference Lucier15] and use them to state theorem 2.8, which is a ‘linearized’ version of theorem 2.6. Finally, we provide a sketch of the subsequent transference argument we will use to deduce theorem 2.6 from theorem 2.8.
In §3, we introduce formally the ‘linearization’ procedure, which we will use to infer theorem 2.6 from theorem 2.8. We apply the W-trick and introduce the majorant ν, the latter of which is the focus of our investigations in §5 and §6. To expedite this process, we record in §4 some general results on exponential sums over primes. These will later be used in §5 and §9.
In §5, we study the Fourier transform of our majorant ν by using the Hardy–Littlewood circle method. We follow this in §6 by investigating the restriction properties of ν and a related majorant µD. The Fourier decay and restriction estimates we obtain in these sections are then applied in §7 to execute the transference principle. This completes the deduction of theorem 2.6 from theorem 2.8.
The focus of the final two sections is to prove theorem 2.8 using an arithmetic regularity lemma. In §8, we begin this argument by first modifying theorem 2.8 into a new result (theorem 8.1), which is more amenable to arithmetic regularity methods. This reduces matters to counting primes in ‘polynomial Bohr sets’. Finally, in §9, we prove theorem 8.1 by establishing density estimates for these prime polynomial Bohr sets.
1.3. Notation
Let ![]() $\mathbb{N}$ denote the set of positive integers, and write
$\mathbb{N}$ denote the set of positive integers, and write ![]() $\mathcal P$ for the set of prime numbers. For each prime p, let
$\mathcal P$ for the set of prime numbers. For each prime p, let ![]() $\mathbb{Q}_p$ and
$\mathbb{Q}_p$ and ![]() $\mathbb{Z}_p$ denote the p-adic numbers and the p-adic integers, respectively. Given a real number X > 0, we write
$\mathbb{Z}_p$ denote the p-adic numbers and the p-adic integers, respectively. Given a real number X > 0, we write ![]() $[X] =
\{n\in\mathbb{N}:
n\leqslant X\}$ and
$[X] =
\{n\in\mathbb{N}:
n\leqslant X\}$ and ![]() $\mathcal P_X =\mathcal P\cap[X]$. Set
$\mathcal P_X =\mathcal P\cap[X]$. Set ![]() $\mathbb{T} = [0,1]$. For each
$\mathbb{T} = [0,1]$. For each ![]() $d\in\mathbb{N}$ and
$d\in\mathbb{N}$ and ![]() $\boldsymbol{\alpha}=(\alpha_1,\ldots,\alpha_d)\in\mathbb{R}^d$, we define
$\boldsymbol{\alpha}=(\alpha_1,\ldots,\alpha_d)\in\mathbb{R}^d$, we define
 \begin{equation*}
\lVert \boldsymbol{\alpha}\rVert = \max_{1\leqslant i\leqslant d}\min_{n\in\mathbb{Z}}|\alpha_i - n| = \min_{{\mathbf{n}}\in\mathbb{Z}^d}\lVert \boldsymbol{\alpha} - {\mathbf{n}}\rVert_\infty.
\end{equation*}
\begin{equation*}
\lVert \boldsymbol{\alpha}\rVert = \max_{1\leqslant i\leqslant d}\min_{n\in\mathbb{Z}}|\alpha_i - n| = \min_{{\mathbf{n}}\in\mathbb{Z}^d}\lVert \boldsymbol{\alpha} - {\mathbf{n}}\rVert_\infty.
\end{equation*} For ![]() $q \in \mathbb{N}$ and
$q \in \mathbb{N}$ and ![]() $x \in \mathbb{R}$, we write
$x \in \mathbb{R}$, we write ![]() $e(x) = e^{2 \pi i x}$ and
$e(x) = e^{2 \pi i x}$ and ![]() $e_q(x) = e(x/q)$. For
$e_q(x) = e(x/q)$. For ![]() $h(x) \in \mathbb{Z}[x]$ and
$h(x) \in \mathbb{Z}[x]$ and ![]() $\mathbf{x} = (x_1,\ldots,x_s)$, where
$\mathbf{x} = (x_1,\ldots,x_s)$, where ![]() $s \in \mathbb{N}$, we abbreviate
$s \in \mathbb{N}$, we abbreviate ![]() $h(\mathbf{x}) = (h(x_1),\ldots,h(x_s))$. If L is a polynomial with integer coefficients, we write
$h(\mathbf{x}) = (h(x_1),\ldots,h(x_s))$. If L is a polynomial with integer coefficients, we write ![]() $\gcd(L)$ for the greatest common divisor of its coefficients. The letter ɛ denotes a small, positive constant, whose value is allowed to differ between separate occurrences.
$\gcd(L)$ for the greatest common divisor of its coefficients. The letter ɛ denotes a small, positive constant, whose value is allowed to differ between separate occurrences.
We employ the Vinogradov and Bachmann–Landau asymptotic notations: for complex-valued functions f and g, we write ![]() $f\ll g$ or
$f\ll g$ or ![]() $g\gg f$ or
$g\gg f$ or ![]() $f=O(g)$ if there exists a constant C such that
$f=O(g)$ if there exists a constant C such that ![]() $|f(x)|\leqslant C|g(x)|$ holds for all x. We indicate the dependence of the implicit constant C on some parameters
$|f(x)|\leqslant C|g(x)|$ holds for all x. We indicate the dependence of the implicit constant C on some parameters ![]() $\lambda_1,\ldots,\lambda_t$ using subscripts, for example,
$\lambda_1,\ldots,\lambda_t$ using subscripts, for example, ![]() $f\ll_{\lambda_1,\ldots,\lambda_t}g$ or
$f\ll_{\lambda_1,\ldots,\lambda_t}g$ or ![]() $f=O_{\lambda_1,\ldots,\lambda_t}(g)$. We write
$f=O_{\lambda_1,\ldots,\lambda_t}(g)$. We write ![]() $f\asymp g$ if
$f\asymp g$ if ![]() $f\ll g$ and
$f\ll g$ and ![]() $g\ll f$ both hold. In any statement in which ɛ appears, we assert that the statement holds for all sufficiently small ɛ > 0.
$g\ll f$ both hold. In any statement in which ɛ appears, we assert that the statement holds for all sufficiently small ɛ > 0.
For a finitely supported function ![]() $f: \mathbb{Z} \to \mathbb{C}$, the Fourier transform
$f: \mathbb{Z} \to \mathbb{C}$, the Fourier transform ![]() $\hat{f}$ is defined by
$\hat{f}$ is defined by
 \begin{equation*}
\hat f({\alpha}) := \sum_{n \in \mathbb{Z}} f(n) e({\alpha} n) \qquad ({\alpha} \in \mathbb{R}).
\end{equation*}
\begin{equation*}
\hat f({\alpha}) := \sum_{n \in \mathbb{Z}} f(n) e({\alpha} n) \qquad ({\alpha} \in \mathbb{R}).
\end{equation*} Given a real-valued function G, which is bounded over a closed interval ![]() $[a,b]$, we write
$[a,b]$, we write
 \begin{equation*}
\lVert G\rVert_{L^\infty[a,b]}:=\sup_{a\leqslant t\leqslant b}|G(t)|.
\end{equation*}
\begin{equation*}
\lVert G\rVert_{L^\infty[a,b]}:=\sup_{a\leqslant t\leqslant b}|G(t)|.
\end{equation*} If G is continuously differentiable on an open interval containing ![]() $[a,b]$, then we define
$[a,b]$, then we define
2. Preliminaries
2.1. Useful ingredients
We will make repeated use of the Siegel–Walfisz theorem [Reference Hua10, lemma 7.14], which we now state for convenience. Recall that the logarithmic integral is given by
 \begin{equation*}
{\mathrm{Li}}(x) = \int_2^x \frac{{\,{\rm d}} t}{\log t} \qquad (x \geqslant 2).
\end{equation*}
\begin{equation*}
{\mathrm{Li}}(x) = \int_2^x \frac{{\,{\rm d}} t}{\log t} \qquad (x \geqslant 2).
\end{equation*}Theorem 2.1 (Siegel–Walfisz theorem)
Let ![]() $P \geqslant 2$, and write
$P \geqslant 2$, and write ![]() $L = \log P$. Let A > 0. Then, there exists
$L = \log P$. Let A > 0. Then, there exists ![]() $c = c(A) \gt 0$ such that the following is true. Let
$c = c(A) \gt 0$ such that the following is true. Let ![]() $n,q,a \in \mathbb{Z}$ with
$n,q,a \in \mathbb{Z}$ with
Then,
 \begin{equation*}
\# \{p \leqslant n: p \equiv a \;(\operatorname{mod}{q}) \} = \frac{{\mathrm{Li}}(n)}{\varphi(q)}
+ O(Pe^{-c \sqrt{\log L}}).
\end{equation*}
\begin{equation*}
\# \{p \leqslant n: p \equiv a \;(\operatorname{mod}{q}) \} = \frac{{\mathrm{Li}}(n)}{\varphi(q)}
+ O(Pe^{-c \sqrt{\log L}}).
\end{equation*}We will also make repeated use of [Reference Rice19, lemma 9], which we state below. Owing to an inaccuracy in the published version of Rice’s article, we cite a later arXiv version. This is also explained in a remark immediately following [Reference Rice19, lemma 9]. The fact that C only depends on the degree comes from the proof.
Lemma 2.2. For any integer ![]() $k\geqslant 2$, there exists
$k\geqslant 2$, there exists ![]() $C = C(k) \gt 0$ such that the following holds. Let
$C = C(k) \gt 0$ such that the following holds. Let ![]() $g(x) = a_k x^k + \cdots + a_1 x + a_0 \in \mathbb{Z}[x]$, and let
$g(x) = a_k x^k + \cdots + a_1 x + a_0 \in \mathbb{Z}[x]$, and let ![]() $W, b \in \mathbb{Z}$. Let
$W, b \in \mathbb{Z}$. Let ![]() $a \in \mathbb{Z}$ and
$a \in \mathbb{Z}$ and ![]() $q \in \mathbb{N}$ be coprime. Let
$q \in \mathbb{N}$ be coprime. Let ![]() ${\omega}(q)$ denote the number of distinct prime factors of q. Let
${\omega}(q)$ denote the number of distinct prime factors of q. Let ![]() $q = q_1 q_2$, where q 2 is the greatest divisor of q that is coprime to W, and let
$q = q_1 q_2$, where q 2 is the greatest divisor of q that is coprime to W, and let ![]() ${\mathrm{cont}}(g) = \gcd(a_1,\ldots,a_k)$. Then,
${\mathrm{cont}}(g) = \gcd(a_1,\ldots,a_k)$. Then,
 \begin{equation*}
\left|
\sum_{\substack{\ell=0\\(W\ell+b,q)=1}}^{q-1}
e_q(ag(\ell))
\right| \leqslant C^{{\omega}(q)}
\left(
\gcd({\mathrm{cont}}(g),q_1) \gcd(a_k,q_2)
\right)^{1/k}
q^{1-1/k}.
\end{equation*}
\begin{equation*}
\left|
\sum_{\substack{\ell=0\\(W\ell+b,q)=1}}^{q-1}
e_q(ag(\ell))
\right| \leqslant C^{{\omega}(q)}
\left(
\gcd({\mathrm{cont}}(g),q_1) \gcd(a_k,q_2)
\right)^{1/k}
q^{1-1/k}.
\end{equation*} We note from its proof that the general epsilon-removal lemma [Reference Salmensuu21, lemma 25] holds with ![]() $\| {\alpha} - a/q \|^{\kappa}$ in place of
$\| {\alpha} - a/q \|^{\kappa}$ in place of ![]() $\| {\alpha} - a/q \|$, and for complex-valued f, with the notation therein. For convenience, we state this version below.
$\| {\alpha} - a/q \|$, and for complex-valued f, with the notation therein. For convenience, we state this version below.
Lemma 2.3. (Epsilon-removal lemma)
Let ![]() ${\kappa}, \epsilon \gt 0$,
${\kappa}, \epsilon \gt 0$, ![]() $N \in \mathbb{N}$,
$N \in \mathbb{N}$, ![]() $K \geqslant 1$,
$K \geqslant 1$, ![]() $u \gt 2/{\kappa}$, and
$u \gt 2/{\kappa}$, and ![]() $v \gt u + \epsilon$. Let
$v \gt u + \epsilon$. Let ![]() $\phi: [N] \to [0,\infty)$ and
$\phi: [N] \to [0,\infty)$ and ![]() $f: [N] \to \mathbb{C}$ with
$f: [N] \to \mathbb{C}$ with
Let C be a large, positive constant, and let
Let ![]() $\mathfrak M$ be the union of the sets
$\mathfrak M$ be the union of the sets
over coprime integers ![]() $0 \leqslant a \leqslant q \leqslant Q$. Assume that
$0 \leqslant a \leqslant q \leqslant Q$. Assume that
 \begin{equation*}
\sum_{n \leqslant N} \phi(n) \ll N, \qquad
\| \hat f \|_u^u \ll K N^{u-1}.
\end{equation*}
\begin{equation*}
\sum_{n \leqslant N} \phi(n) \ll N, \qquad
\| \hat f \|_u^u \ll K N^{u-1}.
\end{equation*}Assume, further, that
 \begin{equation*}
\hat \phi({\alpha}) \ll
\frac{q^{-{\kappa}}N}{1 + N \| {\alpha} - a/q \|^{\kappa}} + o(K^{-2/\epsilon}N)
\qquad ({\alpha} \in \mathfrak M)
\end{equation*}
\begin{equation*}
\hat \phi({\alpha}) \ll
\frac{q^{-{\kappa}}N}{1 + N \| {\alpha} - a/q \|^{\kappa}} + o(K^{-2/\epsilon}N)
\qquad ({\alpha} \in \mathfrak M)
\end{equation*}and
 \begin{equation*}
\hat \phi({\alpha}) = o(K^{-2/\epsilon}N)
\qquad ({\alpha} \notin \mathfrak M).
\end{equation*}
\begin{equation*}
\hat \phi({\alpha}) = o(K^{-2/\epsilon}N)
\qquad ({\alpha} \notin \mathfrak M).
\end{equation*}Then,
 \begin{equation*}
\| \hat f \|_v^v \ll_v N^{v-1}.
\end{equation*}
\begin{equation*}
\| \hat f \|_v^v \ll_v N^{v-1}.
\end{equation*} Here, ![]() $o(K^{-2/\epsilon}N)$ denotes any quantity X such that if c > 0 and N is sufficiently large, then
$o(K^{-2/\epsilon}N)$ denotes any quantity X such that if c > 0 and N is sufficiently large, then
This quantity may differ between instances.
2.2. Necessary conditions
We now provide necessary conditions for Eq. (1.3) to be partition or density regular over the primes. To state our results, we recall that an integer polynomial h is called intersective (or intersective of the first kind) if, for each ![]() $n\in\mathbb{N}$, there exists
$n\in\mathbb{N}$, there exists ![]() $x\in\mathbb{Z}$ such that
$x\in\mathbb{Z}$ such that ![]() $h(x)\equiv 0\;(\operatorname{mod}{n})$. We call h intersective of the second kind if this statement holds under the additional condition such that an x can be found, which is coprime to n. The following lemma demonstrates that intersectivity is a necessary condition for partition regularity of general polynomial equations.
$h(x)\equiv 0\;(\operatorname{mod}{n})$. We call h intersective of the second kind if this statement holds under the additional condition such that an x can be found, which is coprime to n. The following lemma demonstrates that intersectivity is a necessary condition for partition regularity of general polynomial equations.
Lemma 2.4. Let ![]() $s\in\mathbb{N}$ and let
$s\in\mathbb{N}$ and let ![]() $F\in\mathbb{Z}[x_1,\ldots,x_s]$. Consider the equation
$F\in\mathbb{Z}[x_1,\ldots,x_s]$. Consider the equation
Proof. Suppose (2.1) is partition regular. Let ![]() $n\in\mathbb{N}$ and consider the n-colouring of
$n\in\mathbb{N}$ and consider the n-colouring of ![]() $\mathbb{N}$ defined by partitioning
$\mathbb{N}$ defined by partitioning ![]() $\mathbb{N}$ into distinct residue classes modulo n. The existence of a monochromatic solution to (2.1) with respect to this colouring implies that
$\mathbb{N}$ into distinct residue classes modulo n. The existence of a monochromatic solution to (2.1) with respect to this colouring implies that ![]() $F(t,\ldots,t)\equiv 0 \;(\operatorname{mod}{n})$ holds for some
$F(t,\ldots,t)\equiv 0 \;(\operatorname{mod}{n})$ holds for some ![]() $t\in[n]$. As n was arbitrary, it follows that
$t\in[n]$. As n was arbitrary, it follows that ![]() $F(x,\ldots,x)$ is intersective.
$F(x,\ldots,x)$ is intersective.
Now suppose (2.1) is partition regular over the primes. Let ![]() $n\in\mathbb{N}$. As before, we partition into residue classes modulo n and infer the existence of
$n\in\mathbb{N}$. As before, we partition into residue classes modulo n and infer the existence of ![]() $t\in[n]$ and primes
$t\in[n]$ and primes ![]() $p_1,\ldots,p_s$, which are not all equal, with
$p_1,\ldots,p_s$, which are not all equal, with ![]() $p_1\equiv \ldots \equiv p_s\equiv t\;(\operatorname{mod}{n})$ such that
$p_1\equiv \ldots \equiv p_s\equiv t\;(\operatorname{mod}{n})$ such that ![]() $F(p_1,\ldots,p_s)=0$. If we take n to be a prime power, then, since the pi are not all equal, at least one pj is coprime to n, whence t and n are coprime. Applying the Chinese remainder theorem, we conclude that
$F(p_1,\ldots,p_s)=0$. If we take n to be a prime power, then, since the pi are not all equal, at least one pj is coprime to n, whence t and n are coprime. Applying the Chinese remainder theorem, we conclude that ![]() $F(x,\ldots,x)$ is intersective of the second kind.
$F(x,\ldots,x)$ is intersective of the second kind.
Finally, suppose (2.1) is density regular or density regular over the primes. Let ![]() $m\in\mathbb{N}$. By the Siegel–Walfisz theorem (in the case of density regularity over the primes), for each prime
$m\in\mathbb{N}$. By the Siegel–Walfisz theorem (in the case of density regularity over the primes), for each prime ![]() $p\nmid m$, we can find an integer/prime solution
$p\nmid m$, we can find an integer/prime solution ![]() $(x_1,\ldots,x_s)$ to (2.1) with
$(x_1,\ldots,x_s)$ to (2.1) with ![]() $x_1\equiv \dots \equiv x_s\equiv m\;(\operatorname{mod}{p})$. By reducing (2.1) modulo p, we deduce that
$x_1\equiv \dots \equiv x_s\equiv m\;(\operatorname{mod}{p})$. By reducing (2.1) modulo p, we deduce that ![]() $F(m,\ldots,m)$ is divisible by infinitely many primes, whence
$F(m,\ldots,m)$ is divisible by infinitely many primes, whence ![]() $F(m,\ldots,m)=0$. As m was arbitrary, we conclude that
$F(m,\ldots,m)=0$. As m was arbitrary, we conclude that ![]() $F(x,\ldots,x)$ is the zero polynomial.
$F(x,\ldots,x)$ is the zero polynomial.
We now apply this lemma to (1.3) to establish the ‘only if’ parts of theorem 1.1. By working modulo ![]() $|\mu| n$ for any
$|\mu| n$ for any ![]() $n \in \mathbb{N}$, we see that if
$n \in \mathbb{N}$, we see that if ![]() $\mu \ne 0$ and
$\mu \ne 0$ and ![]() $\mu h$ is intersective of the second kind, then so too is h. Note also that the following result does not impose any restriction on the number of variables:
$\mu h$ is intersective of the second kind, then so too is h. Note also that the following result does not impose any restriction on the number of variables:
Corollary 2.5. Let ![]() $s\in\mathbb{N}$ and let h be an integer polynomial of positive degree. Let
$s\in\mathbb{N}$ and let h be an integer polynomial of positive degree. Let ![]() $a_1,\ldots,a_s$ be non-zero integers, and let b be an integer.
$a_1,\ldots,a_s$ be non-zero integers, and let b be an integer.
(PR) If (1.3) is partition regular over the primes, then there exist a non-empty set
 $I\subseteq\{1,\ldots,s\}$ with
$I\subseteq\{1,\ldots,s\}$ with  $\sum_{i\in I}a_i =0$ and an integer m with
$\sum_{i\in I}a_i =0$ and an integer m with  $b=(a_{1}+\cdots +a_s)m$ such that
$b=(a_{1}+\cdots +a_s)m$ such that  $h(x) - m$ is an intersective polynomial of the second kind.
$h(x) - m$ is an intersective polynomial of the second kind.(DR) If (1.3) is density regular or density regular over the primes, then
 $b=a_1 +\cdots +a_s = 0$.
$b=a_1 +\cdots +a_s = 0$.
Proof. Throughout this proof, we write ![]() $\mu =a_1+\cdots+a_s$ and
$\mu =a_1+\cdots+a_s$ and ![]() $H(x) =\mu h(x) - b$. First suppose (1.3) is partition regular over the primes. Applying lemma 2.4 to the polynomial
$H(x) =\mu h(x) - b$. First suppose (1.3) is partition regular over the primes. Applying lemma 2.4 to the polynomial ![]() $F(x_1,\ldots,x_s) = a_1x_1 + \cdots + a_sx_s - b$, we find that H(x) is intersective of the second kind. By considering solutions to
$F(x_1,\ldots,x_s) = a_1x_1 + \cdots + a_sx_s - b$, we find that H(x) is intersective of the second kind. By considering solutions to ![]() $H(x)\equiv 0\;(\operatorname{mod}{d})$ for any
$H(x)\equiv 0\;(\operatorname{mod}{d})$ for any ![]() $d\mid \mu$, we observe that
$d\mid \mu$, we observe that ![]() $\mu\mid b$. If µ ≠ 0, then there is a unique
$\mu\mid b$. If µ ≠ 0, then there is a unique ![]() $m\in\mathbb{Z}$ with
$m\in\mathbb{Z}$ with ![]() $b=\mu m$ such that
$b=\mu m$ such that ![]() $H(x)=\mu(h(x) - m)$, whence
$H(x)=\mu(h(x) - m)$, whence ![]() $h(x)-m$ is intersective of the second kind. If µ = 0, then b = 0, and so, upon taking
$h(x)-m$ is intersective of the second kind. If µ = 0, then b = 0, and so, upon taking ![]() $m=h(1)$, we have
$m=h(1)$, we have ![]() $b=\mu m$, and
$b=\mu m$, and ![]() $h(x)-m$ is trivially intersective of the second kind. In both cases, Eq. (1.3) becomes
$h(x)-m$ is trivially intersective of the second kind. In both cases, Eq. (1.3) becomes
 \begin{equation*}
\sum_{i=1}^{s} a_i(h(x_i) - m) = 0,
\end{equation*}
\begin{equation*}
\sum_{i=1}^{s} a_i(h(x_i) - m) = 0,
\end{equation*} for some ![]() $m\in\mathbb{Z}$ such that
$m\in\mathbb{Z}$ such that ![]() $h(x)-m$ is intersective of the second kind. As this new equation is partition regular, we infer from [Reference Chapman and Chow2, proposition 2.1] the existence of a set
$h(x)-m$ is intersective of the second kind. As this new equation is partition regular, we infer from [Reference Chapman and Chow2, proposition 2.1] the existence of a set ![]() $I\subseteq\{1,\ldots,s\}$ with the desired properties.
$I\subseteq\{1,\ldots,s\}$ with the desired properties.
Finally, suppose that (1.3) is density regular or density regular over the primes. Then, lemma 2.4 implies that ![]() $H(x) = \mu h(x) - b$ is the zero polynomial. Since h has positive degree, we conclude that
$H(x) = \mu h(x) - b$ is the zero polynomial. Since h has positive degree, we conclude that ![]() $b=\mu=0$.
$b=\mu=0$.
In view of these necessary conditions, theorem 1.1 is now an immediate consequence of theorem 1.5.
2.3. Linear form equations
Having dispensed with the necessary conditions for partition and density regularity, we focus on finding monochromatic or dense solutions to (1.3). The necessary conditions we have established, therefore, inform us that (1.3) takes the shape
 \begin{equation*}
\sum_{i\in I}a_i (h(x_i)-m) = -\sum_{j\in[s]\setminus I}a_j (h(x_j)-m),
\end{equation*}
\begin{equation*}
\sum_{i\in I}a_i (h(x_i)-m) = -\sum_{j\in[s]\setminus I}a_j (h(x_j)-m),
\end{equation*} where ![]() $I\subseteq [s]$ is non-empty with
$I\subseteq [s]$ is non-empty with ![]() $\sum_{i\in I}a_i=0$, and
$\sum_{i\in I}a_i=0$, and ![]() $m\in\mathbb{Z}$ is such that
$m\in\mathbb{Z}$ is such that ![]() $b=(a_1+\cdots+a_s)m$ and
$b=(a_1+\cdots+a_s)m$ and ![]() $h(x)-m$ is intersective of the second kind. Upon replacing h(x) with
$h(x)-m$ is intersective of the second kind. Upon replacing h(x) with ![]() $h(x)-m$, we can therefore reduce to the case where b = 0 and h(x) is intersective of the second kind.
$h(x)-m$, we can therefore reduce to the case where b = 0 and h(x) is intersective of the second kind.
To find monochromatic or dense solutions to (1.3) with b = 0, we study equations of the form
for some linear forms L 1 and L 2. To avoid trivialities, we only consider non-degenerate linear forms, where ![]() $L(\mathbf{x})=a_1x_1 + \cdots + a_sx_s$ is non-degenerate if
$L(\mathbf{x})=a_1x_1 + \cdots + a_sx_s$ is non-degenerate if ![]() $a_i\neq 0$ for all
$a_i\neq 0$ for all ![]() $i\in[s]$. For this new equation, the necessary conditions for partition and density regularity become
$i\in[s]$. For this new equation, the necessary conditions for partition and density regularity become ![]() $L_1(1,\ldots,1)=0$. Following the recent works [Reference Chapman and Chow2, Reference Chow, Lindqvist and Prendiville5], we address both density and partition regularity for (2.2) simultaneously by seeking solutions where the xi variables are sourced in a dense subset of
$L_1(1,\ldots,1)=0$. Following the recent works [Reference Chapman and Chow2, Reference Chow, Lindqvist and Prendiville5], we address both density and partition regularity for (2.2) simultaneously by seeking solutions where the xi variables are sourced in a dense subset of ![]() $\mathcal P_X$, while the remaining yj variables come from a colour class
$\mathcal P_X$, while the remaining yj variables come from a colour class ![]() $\mathcal C_k\subseteq \mathcal P_X$.
$\mathcal C_k\subseteq \mathcal P_X$.
Before proceeding to our results, we require some notation. We begin by providing an explicit description of the threshold ![]() $s_0(d)$ for the number of variables required in our main theorems. Let
$s_0(d)$ for the number of variables required in our main theorems. Let ![]() $T = T(d) \in \mathbb{N}$ be minimal such that if
$T = T(d) \in \mathbb{N}$ be minimal such that if ![]() $h(x) \in \mathbb{Z}[x]$ has degree d, then
$h(x) \in \mathbb{Z}[x]$ has degree d, then
has ![]() $O_{h,\varepsilon}(X^{2T - d + \varepsilon})$ solutions
$O_{h,\varepsilon}(X^{2T - d + \varepsilon})$ solutions ![]() $\mathbf{x} \in [X]^{2T}$. Equivalently, by orthogonality,
$\mathbf{x} \in [X]^{2T}$. Equivalently, by orthogonality, ![]() $T = T(d)$ is the smallest positive integer such that the moment estimate
$T = T(d)$ is the smallest positive integer such that the moment estimate
 \begin{equation*}
\int_{\mathbb{T}}\left\lvert \sum_{x\leqslant X}e(\alpha h(x))\right\rvert^{2T}\ll_{h,\varepsilon} X^{2T-d+\varepsilon}
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}}\left\lvert \sum_{x\leqslant X}e(\alpha h(x))\right\rvert^{2T}\ll_{h,\varepsilon} X^{2T-d+\varepsilon}
\end{equation*} holds for any integer polynomial h of degree d. The quantity ![]() $s_0(d)$ appearing in theorem 1.1 is now defined to be
$s_0(d)$ appearing in theorem 1.1 is now defined to be ![]() $s_0(d):= 2T(d) + 1$.
$s_0(d):= 2T(d) + 1$.
It follows from Hua’s lemma [Reference Hua9, equation (1)] that ![]() $T(2) \leqslant 2$ and
$T(2) \leqslant 2$ and ![]() $T(3) \leqslant 4$. In general, the proof of [Reference Wooley23, corollary 14.7] delivers
$T(3) \leqslant 4$. In general, the proof of [Reference Wooley23, corollary 14.7] delivers
 \begin{equation*}
T(d) \leqslant \frac{d(d-1)}2 + \lfloor \sqrt{2d+2} \rfloor.
\end{equation*}
\begin{equation*}
T(d) \leqslant \frac{d(d-1)}2 + \lfloor \sqrt{2d+2} \rfloor.
\end{equation*} These observations verify the bound (1.4) for ![]() $s_0(d)$. Finally, by considering solutions with
$s_0(d)$. Finally, by considering solutions with ![]() $x_{i}=x_{i+T}$ for
$x_{i}=x_{i+T}$ for ![]() $i=1,2,\ldots,T$, we record the lower bounds
$i=1,2,\ldots,T$, we record the lower bounds
We can now state our main result on partition and density regularity over primes for linear form equations (2.2).
Theorem 2.6 Let r and ![]() $d\geqslant 2$ be positive integers, and let
$d\geqslant 2$ be positive integers, and let ![]() $0 \lt \delta\leqslant 1$. Let h be an integer polynomial of degree d, which is intersective of the second kind. Let
$0 \lt \delta\leqslant 1$. Let h be an integer polynomial of degree d, which is intersective of the second kind. Let ![]() $s \geqslant 1$ and
$s \geqslant 1$ and ![]() $t \geqslant 0$ be integers such that
$t \geqslant 0$ be integers such that ![]() $s + t \geqslant s_0(d)$. Let
$s + t \geqslant s_0(d)$. Let
be non-degenerate linear forms such that ![]() $L_1(1,\ldots,1) = 0$. Then, there exist
$L_1(1,\ldots,1) = 0$. Then, there exist
such that the following is true for all ![]() $X\geqslant X_0$. Suppose
$X\geqslant X_0$. Suppose ![]() $\mathcal P_X = \mathcal C_1 \cup \cdots \cup \mathcal C_r$. Then, there exists
$\mathcal P_X = \mathcal C_1 \cup \cdots \cup \mathcal C_r$. Then, there exists ![]() $k \in [r]$ with
$k \in [r]$ with ![]() $|\mathcal C_k|\geqslant\tau_0(\delta) |\mathcal P_X|$ such that if
$|\mathcal C_k|\geqslant\tau_0(\delta) |\mathcal P_X|$ such that if ![]() $A \subseteq \mathcal P_X$ satisfies
$A \subseteq \mathcal P_X$ satisfies ![]() $|A| \geqslant {\delta} |\mathcal P_X|$, then
$|A| \geqslant {\delta} |\mathcal P_X|$, then
 \begin{equation*}
\# \{(\mathbf{x}, \mathbf{y}) \in A^s \times \mathcal C_k^t: L_1(h(\mathbf{x})) = L_2(h(\mathbf{y})) \} \gg
\frac{X^{s+t-d}}{(\log X)^{s+t}}.
\end{equation*}
\begin{equation*}
\# \{(\mathbf{x}, \mathbf{y}) \in A^s \times \mathcal C_k^t: L_1(h(\mathbf{x})) = L_2(h(\mathbf{y})) \} \gg
\frac{X^{s+t-d}}{(\log X)^{s+t}}.
\end{equation*} The implied constant may depend on ![]() $h, L_1, L_2, r, \delta$.
$h, L_1, L_2, r, \delta$.
Remark 2.7. In the case t = 0, we have a linear form L 2 in zero variables, and we are counting solutions ![]() $\mathbf{x}\in A^s$ to the equation
$\mathbf{x}\in A^s$ to the equation
Note that when t = 0, all linear forms L 2 in t variables are vacuously non-degenerate.
By harnessing a combinatorial ‘cleaving’ argument of Prendiville [Reference Prendiville17], we can swiftly deduce theorem 1.5 from theorem 2.6.
Proof of theorem 1.5 given theorem 2.6
Following the argument given at the beginning of this subsection, we may reduce to the case where b = 0 and h is intersective of the second kind. Combining [Reference Chapman and Chow2, lemma 3.2] with (2.3), for N sufficiently large, the number of solutions ![]() $\mathbf{x} \in [N]^s$ to (1.3) such that
$\mathbf{x} \in [N]^s$ to (1.3) such that ![]() $x_i = x_j$ holds for some i ≠ j is
$x_i = x_j$ holds for some i ≠ j is ![]() $O_\varepsilon(N^{s-d+\varepsilon-1/2})$. Therefore, by setting t = 0, we see that the density regularity statement in theorem 1.5 follows directly from theorem 2.6. Similarly, given a colouring
$O_\varepsilon(N^{s-d+\varepsilon-1/2})$. Therefore, by setting t = 0, we see that the density regularity statement in theorem 1.5 follows directly from theorem 2.6. Similarly, given a colouring ![]() $\mathcal P_N = \mathcal C_1\cup\cdots\cup\mathcal C_r$, provided N is sufficiently large, it remains to show that there are at least
$\mathcal P_N = \mathcal C_1\cup\cdots\cup\mathcal C_r$, provided N is sufficiently large, it remains to show that there are at least ![]() $c_1N^{-d}(N/\log N)^{s}$ monochromatic solutions to (2.2) with
$c_1N^{-d}(N/\log N)^{s}$ monochromatic solutions to (2.2) with
 \begin{equation*}
L_1(\mathbf{x}):=\sum_{i\in I}a_ix_i, \quad\text{and} \quad L_2(\mathbf{y}):= -\sum_{i\in [s]
\setminus I}a_iy_j.
\end{equation*}
\begin{equation*}
L_1(\mathbf{x}):=\sum_{i\in I}a_ix_i, \quad\text{and} \quad L_2(\mathbf{y}):= -\sum_{i\in [s]
\setminus I}a_iy_j.
\end{equation*} For each δ > 0, let ![]() $\tau_0(\delta)\in(0,1)$ be as given in the statement of theorem 2.6. By making minor adjustments, we may assume that
$\tau_0(\delta)\in(0,1)$ be as given in the statement of theorem 2.6. By making minor adjustments, we may assume that ![]() $\tau_0(\delta)\leqslant\delta$. Set
$\tau_0(\delta)\leqslant\delta$. Set ![]() $\delta_0=1/r$, and for each
$\delta_0=1/r$, and for each ![]() $i\in[r]$, let
$i\in[r]$, let ![]() $\delta_i:=\tau_0(\delta_{i-1})$, whence
$\delta_i:=\tau_0(\delta_{i-1})$, whence ![]() $0 \lt \delta_r\leqslant\ldots\leqslant\delta_0 \lt 1$. Take
$0 \lt \delta_r\leqslant\ldots\leqslant\delta_0 \lt 1$. Take ![]() $N\geqslant X_0(\delta_r,h,r,L_1,L_2)$ as in theorem 2.6, and suppose
$N\geqslant X_0(\delta_r,h,r,L_1,L_2)$ as in theorem 2.6, and suppose ![]() $\mathcal P_N
=\mathcal C_1\cup\cdots\cup\mathcal C_r$. For each
$\mathcal P_N
=\mathcal C_1\cup\cdots\cup\mathcal C_r$. For each ![]() $0\leqslant i\leqslant r$, let
$0\leqslant i\leqslant r$, let ![]() $k_i\in[r]$ be the index given by applying theorem 2.6 with
$k_i\in[r]$ be the index given by applying theorem 2.6 with ![]() $\delta=\delta_i$. By the pigeonhole principle, we can find
$\delta=\delta_i$. By the pigeonhole principle, we can find ![]() $k\in[r]$ and
$k\in[r]$ and ![]() $0\leqslant i \lt j\leqslant r$ such that
$0\leqslant i \lt j\leqslant r$ such that ![]() $k_i=k_j=k$. Therefore,
$k_i=k_j=k$. Therefore,
 \begin{equation*}
\frac{|\mathcal C_k|}{|\mathcal P_N|}
\geqslant \tau_0(\delta_i)
=\delta_{i+1}\geqslant\delta_j,
\end{equation*}
\begin{equation*}
\frac{|\mathcal C_k|}{|\mathcal P_N|}
\geqslant \tau_0(\delta_i)
=\delta_{i+1}\geqslant\delta_j,
\end{equation*}and
 \begin{equation*}
\# \{(\mathbf{x}, \mathbf{y}) \in A^{|I|} \times \mathcal C_k^{s-|I|}: L_1(h(\mathbf{x})) = L_2(h(\mathbf{y})) \} \gg_{\delta_j,h,r,L_1,L_2}
\frac{N^{s-d}}{(\log N)^{s}}
\end{equation*}
\begin{equation*}
\# \{(\mathbf{x}, \mathbf{y}) \in A^{|I|} \times \mathcal C_k^{s-|I|}: L_1(h(\mathbf{x})) = L_2(h(\mathbf{y})) \} \gg_{\delta_j,h,r,L_1,L_2}
\frac{N^{s-d}}{(\log N)^{s}}
\end{equation*} holds for any ![]() $A\subseteq\mathcal P_N$ with
$A\subseteq\mathcal P_N$ with ![]() $|A|\geqslant\delta_j|\mathcal P_N|$. Taking
$|A|\geqslant\delta_j|\mathcal P_N|$. Taking ![]() $A=\mathcal C_k$ finishes the proof.
$A=\mathcal C_k$ finishes the proof.
2.4. Auxiliary intersective polynomials
The next step of our argument is to use a version of Green’s Fourier-analytic transference principle [Reference Green6] to obtain solutions to (2.2) by ‘transferring’ solutions from a ‘linearized’ equation. To make this precise, we first need to introduce the auxiliary intersective polynomials of Lucier [Reference Lucier15], which emerge during the execution of this process.
Let h be an integer polynomial of positive degree d, which is intersective of the second kind. Thus, for each prime p, we can find a p-adic unit ![]() $z_p \in \mathbb{Z}_p^{\times}$ such that
$z_p \in \mathbb{Z}_p^{\times}$ such that ![]() $h(z_p)=0$. Throughout this article, we fix a choice of zp for each prime p and let mp be the multiplicity of zp as a zero of h. For each prime p and positive integer D, let
$h(z_p)=0$. Throughout this article, we fix a choice of zp for each prime p and let mp be the multiplicity of zp as a zero of h. For each prime p and positive integer D, let ![]() $\mathrm{ord}_p(D)$ denote the largest non-negative integer n such that pn divides D. We can then define the completely multiplicative function
$\mathrm{ord}_p(D)$ denote the largest non-negative integer n such that pn divides D. We can then define the completely multiplicative function
 \begin{equation}
{\lambda}(D) := \prod_p p^{m_p \mathrm{ord}_p(D)} \qquad (D\in\mathbb{N}).
\end{equation}
\begin{equation}
{\lambda}(D) := \prod_p p^{m_p \mathrm{ord}_p(D)} \qquad (D\in\mathbb{N}).
\end{equation} By noting that ![]() $1\leqslant m_p\leqslant \mathrm{deg}(h)=d$ for all p, we have
$1\leqslant m_p\leqslant \mathrm{deg}(h)=d$ for all p, we have
For each prime p and non-negative integer k, reducing zp modulo pk reveals that there exists a unique residue ![]() $x\in\mathbb{Z}/p^k\mathbb{Z}$ such that
$x\in\mathbb{Z}/p^k\mathbb{Z}$ such that ![]() $x\equiv z_p \;(\operatorname{mod}{p^k\mathbb{Z}_p})$. By the Chinese remainder theorem, we can therefore find a unique integer rD in the range
$x\equiv z_p \;(\operatorname{mod}{p^k\mathbb{Z}_p})$. By the Chinese remainder theorem, we can therefore find a unique integer rD in the range ![]() $(-D,0]$, which satisfies
$(-D,0]$, which satisfies
 \begin{equation*}
r_D \equiv z_p \;(\operatorname{mod}{p^{\mathrm{ord}_p(D)} \mathbb{Z}_p})
\end{equation*}
\begin{equation*}
r_D \equiv z_p \;(\operatorname{mod}{p^{\mathrm{ord}_p(D)} \mathbb{Z}_p})
\end{equation*} for all primes p. As h is intersective of the second kind, we have ![]() $(r_D, D) = 1$.
$(r_D, D) = 1$.
Finally, with this notation in place, we define the auxiliary intersective polynomial
 \begin{equation*}
h_D(x) := \frac{h(r_D + Dx)}{{\lambda}(D)} \in \mathbb{Z}[x].
\end{equation*}
\begin{equation*}
h_D(x) := \frac{h(r_D + Dx)}{{\lambda}(D)} \in \mathbb{Z}[x].
\end{equation*} These polynomials and the surrounding notation were introduced by Lucier [Reference Lucier15], who also showed that hD is indeed a polynomial with integer coefficients [Reference Lucier15, lemma 21]. The most important property of these auxiliary polynomials is that the greatest common divisor of the non-constant coefficients of hD is bounded uniformly in D. Specifically, for all ![]() $D\in\mathbb{N}$, [Reference Lucier15, lemma 28] states that
$D\in\mathbb{N}$, [Reference Lucier15, lemma 28] states that
As in [Reference Chapman and Chow2, §6], this bound is crucial to our investigation of exponential sums involving intersective polynomials (see §7 and §9).
We can now state our linearized version of theorem 2.6.
Theorem 2.8 Let r and ![]() $d\geqslant 2$ be positive integers, and let
$d\geqslant 2$ be positive integers, and let ![]() $0 \lt \delta\leqslant 1$. Let h be an integer polynomial of degree d which is intersective of the second kind. Let
$0 \lt \delta\leqslant 1$. Let h be an integer polynomial of degree d which is intersective of the second kind. Let ![]() $s \geqslant 1$ and
$s \geqslant 1$ and ![]() $t \geqslant 0$ be integers such that
$t \geqslant 0$ be integers such that ![]() $s + t \geqslant s_0(d)$. Let
$s + t \geqslant s_0(d)$. Let
be non-degenerate linear forms such that ![]() $L_1(1,\ldots,1) = 0$. Then, there exists
$L_1(1,\ldots,1) = 0$. Then, there exists
such that the following is true. Let ![]() $D, Z \in \mathbb{N}$ satisfy
$D, Z \in \mathbb{N}$ satisfy ![]() $Z \geqslant Z_0$, and set
$Z \geqslant Z_0$, and set ![]() $N:=h_D(Z)$. Suppose
$N:=h_D(Z)$. Suppose
Then, there exists ![]() $k \in [r]$ such that if
$k \in [r]$ such that if ![]() $\mathcal A\subseteq[N]$ satisfies
$\mathcal A\subseteq[N]$ satisfies ![]() $|\mathcal A|\geqslant\delta N$, then
$|\mathcal A|\geqslant\delta N$, then
 \begin{equation*}
\# \{({\mathbf{n}},\mathbf{z}) \in \mathcal A^s \times \mathcal C_k^t: L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \} \gg
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t.
\end{equation*}
\begin{equation*}
\# \{({\mathbf{n}},\mathbf{z}) \in \mathcal A^s \times \mathcal C_k^t: L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \} \gg
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t.
\end{equation*} The implied constant may depend on ![]() $h, L_1, L_2, r, \delta$.
$h, L_1, L_2, r, \delta$.
Remark 2.9. The quantity η is introduced for technical reasons concerning certain weight functions νD we employ when applying the transference principle. For further details, see the remarks preceding lemma 8.3.
The proof of theorem 2.8 is deferred to the final two sections of this article. As in [Reference Chapman and Chow2], we prove this ‘linearized’ result by applying an arithmetic regularity lemma. To streamline this forthcoming argument, we require the following proposition, which is a minor variation of [Reference Chapman and Chow2, proposition 3.10] and is proved in the same way.
Proposition 2.10. Suppose that theorem 2.8 is true in the cases where ![]() $\gcd(L_1)=1$. Then, subject to altering the quantities
$\gcd(L_1)=1$. Then, subject to altering the quantities ![]() $Z_0(D,r,\delta,L_1,L_2,P)$, η, and the implicit constant in the final bound, theorem 2.8 holds in general.
$Z_0(D,r,\delta,L_1,L_2,P)$, η, and the implicit constant in the final bound, theorem 2.8 holds in general.
2.5. Sketch of the transference argument
In this subsection, we outline how the transference principle allows us to deduce theorem 2.6 from theorem 2.8. Fix an integer polynomial h that is intersective of the second kind, as well as a pair of linear forms L 1 and L 2 as in the statement of theorem 2.6. We begin by recalling that theorem 2.6 concerns the equation
while theorem 2.8 considers, for some parameter ![]() $D\in\mathbb{N}$, the ‘linearized’ equation
$D\in\mathbb{N}$, the ‘linearized’ equation
Suppose we have a finite colouring ![]() $\mathcal P_X= \mathcal C_1\cup\cdots\cup \mathcal C_r$ and a set
$\mathcal P_X= \mathcal C_1\cup\cdots\cup \mathcal C_r$ and a set ![]() $A\subseteq\mathcal P_X$ with
$A\subseteq\mathcal P_X$ with ![]() $|A|\geqslant\delta|\mathcal P_X|$. For the convenience of this sketch, assume that
$|A|\geqslant\delta|\mathcal P_X|$. For the convenience of this sketch, assume that ![]() $X\equiv r_D \;(\operatorname{mod}{D})$. Choosing
$X\equiv r_D \;(\operatorname{mod}{D})$. Choosing ![]() $Z\in\mathbb{N}$ such that
$Z\in\mathbb{N}$ such that ![]() $X=r_D + DZ$, we can define an r-colouring
$X=r_D + DZ$, we can define an r-colouring
by
Let ![]() $N:=h_D(Z)$. By pigeonholing, we find a ‘dense’ set
$N:=h_D(Z)$. By pigeonholing, we find a ‘dense’ set ![]() $\mathcal A\subseteq[N]$ such that
$\mathcal A\subseteq[N]$ such that
 \begin{equation*}
\mathcal A\subseteq \left\{\frac{h(x)-h(b)}{\lambda(D)}: x \in A \right \},
\end{equation*}
\begin{equation*}
\mathcal A\subseteq \left\{\frac{h(x)-h(b)}{\lambda(D)}: x \in A \right \},
\end{equation*}for some integer b.
Theorem 2.8 now informs us that there are many solutions  $({\mathbf{n}},\mathbf{z})\in \mathcal A^s\times\tilde{\mathcal C}_k^t$ to (2.7) for some
$({\mathbf{n}},\mathbf{z})\in \mathcal A^s\times\tilde{\mathcal C}_k^t$ to (2.7) for some ![]() $k\in[r]$. Given such a solution, our construction of
$k\in[r]$. Given such a solution, our construction of ![]() $\mathcal A$ and
$\mathcal A$ and ![]() $\tilde{\mathcal C}_k$ furnishes a solution
$\tilde{\mathcal C}_k$ furnishes a solution ![]() $(\mathbf{x},\mathbf{y})\in A^s\times\mathcal C_k^t$ to (2.6) satisfying
$(\mathbf{x},\mathbf{y})\in A^s\times\mathcal C_k^t$ to (2.6) satisfying
 \begin{equation*}
n_i = \frac{h(x_i) - h(b)}{\lambda(D)}, \quad y_j = r_D + Dz_j \qquad (1\leqslant i\leqslant s,
\quad
1\leqslant j\leqslant t).
\end{equation*}
\begin{equation*}
n_i = \frac{h(x_i) - h(b)}{\lambda(D)}, \quad y_j = r_D + Dz_j \qquad (1\leqslant i\leqslant s,
\quad
1\leqslant j\leqslant t).
\end{equation*} Since the map ![]() $({\mathbf{n}},\mathbf{z})\mapsto(\mathbf{x},\mathbf{y})$ is injective, this argument allows us to obtain many solutions to (2.6). However, observe that the number of solutions to (2.6) given in theorem 2.6 is
$({\mathbf{n}},\mathbf{z})\mapsto(\mathbf{x},\mathbf{y})$ is injective, this argument allows us to obtain many solutions to (2.6). However, observe that the number of solutions to (2.6) given in theorem 2.6 is ![]() $
X^{s-d+t+o(1)},
$ which is far fewer than the number of solutions to (2.7) provided by theorem 2.8, namely
$
X^{s-d+t+o(1)},
$ which is far fewer than the number of solutions to (2.7) provided by theorem 2.8, namely ![]() $X^{ds - d + t + o(1)}$. This shortfall is handled by instead considering weighted counts of solutions to (2.6). Our task is then to construct an appropriate weight function ν, which is supported on the set
$X^{ds - d + t + o(1)}$. This shortfall is handled by instead considering weighted counts of solutions to (2.6). Our task is then to construct an appropriate weight function ν, which is supported on the set
 \begin{equation*}
[N]\cap\left\{\frac{h(x)-h(b)}{\lambda(D)}: b \lt x \leqslant X\right \}.
\end{equation*}
\begin{equation*}
[N]\cap\left\{\frac{h(x)-h(b)}{\lambda(D)}: b \lt x \leqslant X\right \}.
\end{equation*} The key utility of the transference principle is that, provided our weight function is suitably ‘pseudorandom’, we can find a ‘dense model’ ![]() $g:[N]\to[0,1]$ such that
$g:[N]\to[0,1]$ such that ![]() $\hat{\nu}\approx\hat{g}$. Applying theorem 2.8 to a set of the form
$\hat{\nu}\approx\hat{g}$. Applying theorem 2.8 to a set of the form ![]() $\mathcal A=\{x\in[N]: g(x) \gt c\}$, our argument above allows us to prove theorem 2.6.
$\mathcal A=\{x\in[N]: g(x) \gt c\}$, our argument above allows us to prove theorem 2.6.
To ensure our weight ν is sufficiently pseudorandom, we have to contend with the fact that the set ![]() $h(\mathcal P)$ is not equidistributed in residue classes. This issue prevents one from simply taking ν to be a scaled version of the indicator function of
$h(\mathcal P)$ is not equidistributed in residue classes. This issue prevents one from simply taking ν to be a scaled version of the indicator function of ![]() $h(\mathcal P)$. Fortunately, there is a standard technical manoeuvre, known as the W-trick, developed by Green [Reference Green6] to account for equidistribution modulo small primes. In the setting discussed above, this amounts to demanding that our weight ν is supported on a set of the form
$h(\mathcal P)$. Fortunately, there is a standard technical manoeuvre, known as the W-trick, developed by Green [Reference Green6] to account for equidistribution modulo small primes. In the setting discussed above, this amounts to demanding that our weight ν is supported on a set of the form
 \begin{equation*}
[N]\cap\left\{\frac{h(x)-h(b)}{\lambda(D)}: b \lt x \leqslant X, \quad x\equiv b \;(\operatorname{mod}{W\kappa}) \right\},
\end{equation*}
\begin{equation*}
[N]\cap\left\{\frac{h(x)-h(b)}{\lambda(D)}: b \lt x \leqslant X, \quad x\equiv b \;(\operatorname{mod}{W\kappa}) \right\},
\end{equation*} for some ![]() $W,\kappa\in\mathbb{N}$ such that W is divisible by all primes
$W,\kappa\in\mathbb{N}$ such that W is divisible by all primes ![]() $p\leqslant w$ for some sufficiently large
$p\leqslant w$ for some sufficiently large ![]() $w\in\mathbb{N}$. If we choose
$w\in\mathbb{N}$. If we choose ![]() $D,W,\kappa$ appropriately, then we can ensure that the set
$D,W,\kappa$ appropriately, then we can ensure that the set
 \begin{equation*}
\left\{\frac{h(x)-h(b)}{\lambda(D)}: b \lt x \leqslant X, \quad x\equiv b \;(\operatorname{mod}{W\kappa}) \right\}
\end{equation*}
\begin{equation*}
\left\{\frac{h(x)-h(b)}{\lambda(D)}: b \lt x \leqslant X, \quad x\equiv b \;(\operatorname{mod}{W\kappa}) \right\}
\end{equation*} equidistributes over congruence classes modulo p for any prime ![]() $p\leqslant w$. The contribution of the remaining primes is then subsumed by the error term emerging from the transference of solutions from the ‘dense model’ g to ν. The appearance of the additional parameter
$p\leqslant w$. The contribution of the remaining primes is then subsumed by the error term emerging from the transference of solutions from the ‘dense model’ g to ν. The appearance of the additional parameter ![]() $\kappa\in\mathbb{N}$ here, resulting in a ‘double W-trick’, was the main innovation of our previous work [Reference Chapman and Chow2]. Its purpose is to ensure that
$\kappa\in\mathbb{N}$ here, resulting in a ‘double W-trick’, was the main innovation of our previous work [Reference Chapman and Chow2]. Its purpose is to ensure that ![]() ${\lambda}(D)$ precisely accounts for all common divisors of the values of
${\lambda}(D)$ precisely accounts for all common divisors of the values of ![]() $h(x) - h(b)$, as x ranges over the arithmetic progression b modulo
$h(x) - h(b)$, as x ranges over the arithmetic progression b modulo ![]() $W {\kappa}$.
$W {\kappa}$.
3. Linearization and the W-trick
In this section, we execute the ‘double W-trick’ and construct the weight function ν needed for our application of the transference principle. Throughout this section, we fix the parameters
which appear in theorem 2.6.
3.1. The W-trick
Consider a set ![]() $A \subseteq \mathcal P_X$ with
$A \subseteq \mathcal P_X$ with ![]() $|A| \geqslant {\delta} |\mathcal P_X|$. Let
$|A| \geqslant {\delta} |\mathcal P_X|$. Let ![]() $C \in \mathbb{N}$ be large with respect to the fixed parameters, and let
$C \in \mathbb{N}$ be large with respect to the fixed parameters, and let ![]() $w\in\mathbb{N}$ be large in terms of C. Define
$w\in\mathbb{N}$ be large in terms of C. Define
 \begin{equation*}
M = Cd^2 10^{4w},
\qquad
W = \left(
\prod_{p \leqslant w} p \right)
^{100dw}, \qquad
V = \sqrt W
\end{equation*}
\begin{equation*}
M = Cd^2 10^{4w},
\qquad
W = \left(
\prod_{p \leqslant w} p \right)
^{100dw}, \qquad
V = \sqrt W
\end{equation*}and
 \begin{equation*}
D = W^2,
\qquad
Z = \frac{X - r_D}{D},
\qquad
N = h_D(Z) = \frac{h(X)}{{\lambda}(D)}.
\end{equation*}
\begin{equation*}
D = W^2,
\qquad
Z = \frac{X - r_D}{D},
\qquad
N = h_D(Z) = \frac{h(X)}{{\lambda}(D)}.
\end{equation*} Henceforth, we take ![]() $X\in\mathbb{N}$ sufficiently large in terms of
$X\in\mathbb{N}$ sufficiently large in terms of ![]() $C,w,$ and the fixed parameters. We also assume that
$C,w,$ and the fixed parameters. We also assume that ![]() $D\mid(X-r_D)$, whence
$D\mid(X-r_D)$, whence ![]() $Z \in \mathbb{N}$.
$Z \in \mathbb{N}$.
For ![]() $R \in \mathbb{N}$ and
$R \in \mathbb{N}$ and ![]() $b \in [R]$, we write
$b \in [R]$, we write
We denote by ![]() $(H,W)_d$ the greatest
$(H,W)_d$ the greatest ![]() $m \in \mathbb{N}$ for which
$m \in \mathbb{N}$ for which ![]() $m^d \mid (H,W)$. By [Reference Chapman and Chow2, lemma A.5] and the Siegel–Walfisz theorem, we have
$m^d \mid (H,W)$. By [Reference Chapman and Chow2, lemma A.5] and the Siegel–Walfisz theorem, we have
 \begin{equation*}
\delta|\mathcal P_X| \leqslant |A| \leqslant
\sum_{\substack{
b \in [W]: \\
(b,W) = 1 \\
(h'(b),W)_d \leqslant M}} |A_{b,W}| +
O\left(10^w W M^{-1/2}
\frac{X}{\varphi(W) \log X}
\right).
\end{equation*}
\begin{equation*}
\delta|\mathcal P_X| \leqslant |A| \leqslant
\sum_{\substack{
b \in [W]: \\
(b,W) = 1 \\
(h'(b),W)_d \leqslant M}} |A_{b,W}| +
O\left(10^w W M^{-1/2}
\frac{X}{\varphi(W) \log X}
\right).
\end{equation*} Since w is large relative to C and d, we have ![]() $M \lt 2^{50w}$. Hence, if
$M \lt 2^{50w}$. Hence, if ![]() $(h'(b),W)_d \leqslant M$, then there cannot exist a prime
$(h'(b),W)_d \leqslant M$, then there cannot exist a prime ![]() $p\leqslant w$, which divides
$p\leqslant w$, which divides ![]() $(h'(b),W)$ with multiplicity greater than 50dw. It follows that if
$(h'(b),W)$ with multiplicity greater than 50dw. It follows that if ![]() $(h'(b),W)_d \leqslant M$, then
$(h'(b),W)_d \leqslant M$, then ![]() $(h'(b),W)\mid V$. By incorporating the crude estimate
$(h'(b),W)\mid V$. By incorporating the crude estimate
 \begin{equation*}
\frac{W}{\varphi(W)} = \prod_{p\leqslant w}\left( 1- \frac{1}{p}\right)^{-1} \leqslant 2^w,
\end{equation*}
\begin{equation*}
\frac{W}{\varphi(W)} = \prod_{p\leqslant w}\left( 1- \frac{1}{p}\right)^{-1} \leqslant 2^w,
\end{equation*}we find that
 \begin{equation*}
\frac{{\delta} X}{\log X}
\ll \sum_{\substack{
b \in [W]: \\
(b,W) = 1 \\
(h'(b),W) \mid V}} |A_{b,W}|.
\end{equation*}
\begin{equation*}
\frac{{\delta} X}{\log X}
\ll \sum_{\substack{
b \in [W]: \\
(b,W) = 1 \\
(h'(b),W) \mid V}} |A_{b,W}|.
\end{equation*} Thus, there exists ![]() $b_0 \in [W]$ such that
$b_0 \in [W]$ such that
 \begin{equation*}
|A_{b_0,W}| \gg
\frac{{\delta} X}{\varphi(W) \log X},
\qquad
(b_0, W) = 1,
\qquad
(h'(b_0),W) \mid V.
\end{equation*}
\begin{equation*}
|A_{b_0,W}| \gg
\frac{{\delta} X}{\varphi(W) \log X},
\qquad
(b_0, W) = 1,
\qquad
(h'(b_0),W) \mid V.
\end{equation*} Define ![]() ${\kappa} \in \mathbb{N}$ by
${\kappa} \in \mathbb{N}$ by
Note that (2.4) implies that κ is w-smooth, whence ![]() $\varphi(W)\kappa = \varphi(W\kappa)$. By pigeonholing, we can then find
$\varphi(W)\kappa = \varphi(W\kappa)$. By pigeonholing, we can then find ![]() $b \in [W {\kappa}]$ such that
$b \in [W {\kappa}]$ such that
 \begin{equation*}
b \equiv b_0 \;(\operatorname{mod}{W}),
\qquad
|A_{b,W{\kappa}}| \gg
\frac{{\delta} X}{\varphi(W) {\kappa} \log X}
= \frac{{\delta} X}{\varphi(W{\kappa}) \log X}.
\end{equation*}
\begin{equation*}
b \equiv b_0 \;(\operatorname{mod}{W}),
\qquad
|A_{b,W{\kappa}}| \gg
\frac{{\delta} X}{\varphi(W) {\kappa} \log X}
= \frac{{\delta} X}{\varphi(W{\kappa}) \log X}.
\end{equation*} Since ![]() $(h'(b),W)
= (h'(b_0), W) \mid V$, we also have
$(h'(b),W)
= (h'(b_0), W) \mid V$, we also have
3.2. The weight function
Our next task is to construct an appropriately ‘pseudorandom’ weight function. Let ![]() $w,W$, and κ be as defined in the previous subsection. Fix some
$w,W$, and κ be as defined in the previous subsection. Fix some ![]() $b\in[W\kappa]$, which satisfies
$b\in[W\kappa]$, which satisfies
We then define
 \begin{equation}
\nu: \mathbb{Z} \to [0,\infty),
\qquad
\nu(n) :=
\frac{\varphi(W)}{W(h'(b),W)}
\sum_{\substack{b \lt p \leqslant X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}}) \\ h(p) - h(b) = n {\lambda}(D)}} h'(p) \log p.
\end{equation}
\begin{equation}
\nu: \mathbb{Z} \to [0,\infty),
\qquad
\nu(n) :=
\frac{\varphi(W)}{W(h'(b),W)}
\sum_{\substack{b \lt p \leqslant X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}}) \\ h(p) - h(b) = n {\lambda}(D)}} h'(p) \log p.
\end{equation}Observe that ν is supported on the set
 \begin{equation*}
\left \{n\in\mathbb{N}: n=\frac{h(p) - h(b)}{{\lambda}(D)},\; p\in\mathcal P_X,\; p\equiv b \;(\operatorname{mod}{W\kappa}) \right \}\subseteq [N].
\end{equation*}
\begin{equation*}
\left \{n\in\mathbb{N}: n=\frac{h(p) - h(b)}{{\lambda}(D)},\; p\in\mathcal P_X,\; p\equiv b \;(\operatorname{mod}{W\kappa}) \right \}\subseteq [N].
\end{equation*} Recall from the previous subsection that we are considering a fixed set ![]() $A\subseteq\mathcal P_X$ with
$A\subseteq\mathcal P_X$ with ![]() $|A|\geqslant\delta|\mathcal P_X|$, and that we made a judicious choice of
$|A|\geqslant\delta|\mathcal P_X|$, and that we made a judicious choice of ![]() $b\in[W\kappa]$ so that
$b\in[W\kappa]$ so that ![]() $|A_{b,W\kappa}|$ is suitably dense. For this specific choice of b, let
$|A_{b,W\kappa}|$ is suitably dense. For this specific choice of b, let
 \begin{equation}
\mathcal A = \left \{
\frac{h(p) - h(b)}{{\lambda}(D)}: p \in A_{b,W{\kappa}} \right \}.
\end{equation}
\begin{equation}
\mathcal A = \left \{
\frac{h(p) - h(b)}{{\lambda}(D)}: p \in A_{b,W{\kappa}} \right \}.
\end{equation}Lemma 3.1. Let ![]() $\mathcal A,\nu$ be as defined above. If X is sufficiently large in terms of
$\mathcal A,\nu$ be as defined above. If X is sufficiently large in terms of ![]() $h,\delta,w$, then
$h,\delta,w$, then
 \begin{equation*}
\sum_{n \in \mathcal A} \nu(n) \gg_{\delta} N.
\end{equation*}
\begin{equation*}
\sum_{n \in \mathcal A} \nu(n) \gg_{\delta} N.
\end{equation*}Proof. Let c be a small, positive constant, and let
For X sufficiently large, the Siegel–Walfisz theorem implies that ![]() $|A_{b,W{\kappa}}| \geqslant |\Omega_{b,W\kappa,c}(X)|$. It follows that there exists an injective map
$|A_{b,W{\kappa}}| \geqslant |\Omega_{b,W\kappa,c}(X)|$. It follows that there exists an injective map ![]() $\psi:\Omega_{b,W\kappa,c}(X)\to A_{b,W{\kappa}}$ such that
$\psi:\Omega_{b,W\kappa,c}(X)\to A_{b,W{\kappa}}$ such that ![]() $p\leqslant\psi(p)$ for all
$p\leqslant\psi(p)$ for all ![]() $p\in\Omega_{b,W\kappa,c}(X)$. This implies that
$p\in\Omega_{b,W\kappa,c}(X)$. This implies that
 \begin{equation*}
\sum_{\substack{p \leqslant c{\delta} X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}})}} p^{d-1} \log p \leqslant \sum_{\substack{p \leqslant c{\delta} X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}})}} \psi(p)^{d-1} \log (\psi(p)) \leqslant
\sum_{p \in A_{b,W{\kappa}}} p^{d-1} \log p.
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant c{\delta} X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}})}} p^{d-1} \log p \leqslant \sum_{\substack{p \leqslant c{\delta} X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}})}} \psi(p)^{d-1} \log (\psi(p)) \leqslant
\sum_{p \in A_{b,W{\kappa}}} p^{d-1} \log p.
\end{equation*} Invoking the bound ![]() $h'(x)\ll x^{d-1}$, we deduce that
$h'(x)\ll x^{d-1}$, we deduce that
 \begin{equation*}
\sum_{p \in A_{b,W{\kappa}}} h'(p) \log p \gg \sum_{\substack{p \leqslant c{\delta} X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}})}} p^{d-1} \log p.
\end{equation*}
\begin{equation*}
\sum_{p \in A_{b,W{\kappa}}} h'(p) \log p \gg \sum_{\substack{p \leqslant c{\delta} X \\ p \equiv b \;(\operatorname{mod}{W {\kappa}})}} p^{d-1} \log p.
\end{equation*}By the Siegel–Walfisz theorem again, we thus have
 \begin{equation*}
\sum_{p \in A_{b,W{\kappa}}} h'(p) \log p \gg_{\delta}
\frac{X^d}{\varphi(W {\kappa})}.
\end{equation*}
\begin{equation*}
\sum_{p \in A_{b,W{\kappa}}} h'(p) \log p \gg_{\delta}
\frac{X^d}{\varphi(W {\kappa})}.
\end{equation*}Therefore,
 \begin{equation*}
\frac{W(h'(b),W)}{\varphi(W)}
\sum_{n \in \mathcal A} \nu(n)
= O((W{\kappa})^{d-1} \log W) +
\sum_{p \in A_{b,W{\kappa}}} h'(p) \log p \gg_\delta \frac{X^d}{\varphi(W {\kappa})}.
\end{equation*}
\begin{equation*}
\frac{W(h'(b),W)}{\varphi(W)}
\sum_{n \in \mathcal A} \nu(n)
= O((W{\kappa})^{d-1} \log W) +
\sum_{p \in A_{b,W{\kappa}}} h'(p) \log p \gg_\delta \frac{X^d}{\varphi(W {\kappa})}.
\end{equation*}Thus, for our choice of κ and b, the desired bound now follows from the equalities
 \begin{equation*}
\frac{W(h'(b),W)}{\varphi(W)} = \frac{\lambda(D)}{\kappa \varphi(W)} = \frac{\lambda(D)}{\varphi(W\kappa)}.
\end{equation*}
\begin{equation*}
\frac{W(h'(b),W)}{\varphi(W)} = \frac{\lambda(D)}{\kappa \varphi(W)} = \frac{\lambda(D)}{\varphi(W\kappa)}.
\end{equation*}4. Exponential sums
In this section, we record some results on exponential sums of the form
 \begin{equation}
\sum_{\substack{p \leqslant t \\ p \equiv b \;(\operatorname{mod}{m})}}e(F(p))G(p),
\end{equation}
\begin{equation}
\sum_{\substack{p \leqslant t \\ p \equiv b \;(\operatorname{mod}{m})}}e(F(p))G(p),
\end{equation} where F is a real polynomial, and ![]() $G:(1,\infty)\to \mathbb{R}$ is a continuously differentiable function. We apply these results in §5 to study the Fourier transform
$G:(1,\infty)\to \mathbb{R}$ is a continuously differentiable function. We apply these results in §5 to study the Fourier transform ![]() $\hat{\nu}$ of our weight function ν. The results of this section are also used in §9 to establish density bounds for ‘prime polynomial Bohr sets’.
$\hat{\nu}$ of our weight function ν. The results of this section are also used in §9 to establish density bounds for ‘prime polynomial Bohr sets’.
A standard observation in analytic number theory, going back over a century to Hardy and Littlewood, is that such exponential sums can only be large if their phases exhibit ‘major arc’ behaviour. In the case of (4.1), this means that the leading coefficient of the polynomial F must be very close to a rational number with small denominator. To elucidate this further, we record the following lemma from [Reference Hua10], which considers the situation where the leading coefficient of F is rational. In what follows, and throughout this section, for all ![]() $k \in \mathbb{N}$, let σk be large in terms of k and put
$k \in \mathbb{N}$, let σk be large in terms of k and put ![]() $C_k = 2^{8k} {\sigma}_k$.
$C_k = 2^{8k} {\sigma}_k$.
Lemma 4.1. Let ![]() $m \in \mathbb{N}$ and
$m \in \mathbb{N}$ and ![]() $b \in \mathbb{Z}$ be coprime. Let
$b \in \mathbb{Z}$ be coprime. Let ![]() $F(y) \in \mathbb{R}[y]$ have degree k, and suppose
$F(y) \in \mathbb{R}[y]$ have degree k, and suppose ![]() $a/q$ is its leading coefficient, where
$a/q$ is its leading coefficient, where ![]() $a,q\in\mathbb{Z}$ are coprime and
$a,q\in\mathbb{Z}$ are coprime and
 \begin{equation*}
(\log P)^{C_k} \lt q \leqslant \frac{P^k}{(\log P)^{C_k}}.
\end{equation*}
\begin{equation*}
(\log P)^{C_k} \lt q \leqslant \frac{P^k}{(\log P)^{C_k}}.
\end{equation*}Assume that P is sufficiently large in terms of m. Then,
 \begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e(F(p)) \ll_k \frac{P}{(\log P)^{{\sigma}_k+1}}.
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e(F(p)) \ll_k \frac{P}{(\log P)^{{\sigma}_k+1}}.
\end{equation*}Proof. This follows immediately from [Reference Hua10, theorem 10].
Using this lemma, we can show that (4.1) is small when the leading coefficient of F is ‘minor arc’, meaning that it is not well-approximated by a rational number with denominator at most polylogarithmic in P.
Lemma 4.2. Let ![]() $m\in\mathbb{N}$ and
$m\in\mathbb{N}$ and ![]() $b\in\mathbb{Z}$ be coprime. Let
$b\in\mathbb{Z}$ be coprime. Let ![]() $F(y)\in\mathbb{R}[y]$ have degree k, and let θ be its leading coefficient. Let
$F(y)\in\mathbb{R}[y]$ have degree k, and let θ be its leading coefficient. Let ![]() $G:(1,\infty)\to \mathbb{R}$ be a continuously differentiable function. Assume that P is sufficiently large in terms of m, and that
$G:(1,\infty)\to \mathbb{R}$ be a continuously differentiable function. Assume that P is sufficiently large in terms of m, and that
Then,
 \begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e(F(p)) G(p)\log p \ll_k \frac{P}{(\log P)^{\sigma_k}}\cdot\lVert G\rVert_{\mathcal S[2,P]}.
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e(F(p)) G(p)\log p \ll_k \frac{P}{(\log P)^{\sigma_k}}\cdot\lVert G\rVert_{\mathcal S[2,P]}.
\end{equation*}Proof. By Dirichlet’s approximation theorem, there exist coprime ![]() $q \in \mathbb{N}$ and
$q \in \mathbb{N}$ and ![]() $a \in \mathbb{Z}$ such that
$a \in \mathbb{Z}$ such that
 \begin{equation*}
q \leqslant \frac{P^k}{(\log P)^{2 C_k}},
\qquad
|q {\theta} - a| \leqslant
\frac{(\log P)^{2 C_k}}{P^k}.
\end{equation*}
\begin{equation*}
q \leqslant \frac{P^k}{(\log P)^{2 C_k}},
\qquad
|q {\theta} - a| \leqslant
\frac{(\log P)^{2 C_k}}{P^k}.
\end{equation*}By our assumption, we also have
Thus, ![]() ${\beta} := {\theta} - a/q$ satisfies
${\beta} := {\theta} - a/q$ satisfies
Let ![]() $f(y) = F(y) - {\beta} y^k$. By partial summation [Reference Vaughan22, lemma 2.6], we have
$f(y) = F(y) - {\beta} y^k$. By partial summation [Reference Vaughan22, lemma 2.6], we have
 \begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b\;(\operatorname{mod}{m})}} e(F(p)) G(p)\log p = A(P)\psi(P) - \int_{2}^{P}A(t)\psi'(t) {\,{\rm d}} t,
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b\;(\operatorname{mod}{m})}} e(F(p)) G(p)\log p = A(P)\psi(P) - \int_{2}^{P}A(t)\psi'(t) {\,{\rm d}} t,
\end{equation*}where
 \begin{equation*}
\psi(t) := e(\beta t^k)G(t)\log t, \qquad
A(t) := \sum_{\substack{p \leqslant t \\ p \equiv b \;(\operatorname{mod}{m})}}
e(f(p)).
\end{equation*}
\begin{equation*}
\psi(t) := e(\beta t^k)G(t)\log t, \qquad
A(t) := \sum_{\substack{p \leqslant t \\ p \equiv b \;(\operatorname{mod}{m})}}
e(f(p)).
\end{equation*} We deduce from lemma 4.1 and the trivial bound ![]() $|A(t)| \leqslant t$ that
$|A(t)| \leqslant t$ that
 \begin{equation}
A(t) \ll \frac{P}{(\log P)^{\sigma_k +1}} \qquad \left( 2 \leqslant t \leqslant P \right).
\end{equation}
\begin{equation}
A(t) \ll \frac{P}{(\log P)^{\sigma_k +1}} \qquad \left( 2 \leqslant t \leqslant P \right).
\end{equation}This implies that
It, therefore, remains to estimate
 \begin{equation*}
\int_{2}^{P}A(t)\psi'(t) {\,{\rm d}} t = I_1 + I_2 + I_3 + I_4,
\end{equation*}
\begin{equation*}
\int_{2}^{P}A(t)\psi'(t) {\,{\rm d}} t = I_1 + I_2 + I_3 + I_4,
\end{equation*}where
 \begin{align*}
I_1 = \int_{2}^{P}A(t)G'(t)e(\beta t^k)\log t {\,{\rm d}} t, \quad
& I_2 = \beta k\int_{2}^{P}t^{k-1}A(t)G(t)e(\beta t^k)\log t {\,{\rm d}} t,\\
I_3 = \int_{2}^{P/(\log P)^{\sigma_k}}(A(t)/t)G(t)e(\beta t^k) {\,{\rm d}} t, \quad
&I_4 = \int_{P/(\log P)^{\sigma_k}}^{P}(A(t)/t)G(t)e(\beta t^k) {\,{\rm d}} t.
\end{align*}
\begin{align*}
I_1 = \int_{2}^{P}A(t)G'(t)e(\beta t^k)\log t {\,{\rm d}} t, \quad
& I_2 = \beta k\int_{2}^{P}t^{k-1}A(t)G(t)e(\beta t^k)\log t {\,{\rm d}} t,\\
I_3 = \int_{2}^{P/(\log P)^{\sigma_k}}(A(t)/t)G(t)e(\beta t^k) {\,{\rm d}} t, \quad
&I_4 = \int_{P/(\log P)^{\sigma_k}}^{P}(A(t)/t)G(t)e(\beta t^k) {\,{\rm d}} t.
\end{align*}The bound (4.2) gives
 \begin{equation*}
I_1(\log P)^{\sigma_k} \ll P^2 \max_{2\leqslant t\leqslant P}|G'(t)|.
\end{equation*}
\begin{equation*}
I_1(\log P)^{\sigma_k} \ll P^2 \max_{2\leqslant t\leqslant P}|G'(t)|.
\end{equation*} Similarly, since ![]() $|\beta|\leqslant P^{-k}$, we see that
$|\beta|\leqslant P^{-k}$, we see that
 \begin{equation*}
I_2 (\log P)^{\sigma_k} \ll P \max_{2\leqslant t\leqslant P}|G(t)|.
\end{equation*}
\begin{equation*}
I_2 (\log P)^{\sigma_k} \ll P \max_{2\leqslant t\leqslant P}|G(t)|.
\end{equation*} Using the trivial bound ![]() $|A(t)|\leqslant t$, we have
$|A(t)|\leqslant t$, we have
 \begin{equation*}
I_3(\log P)^{\sigma_k} \ll P\max_{2\leqslant t\leqslant P/(\log P)^{\sigma_k}}|G(t)|.
\end{equation*}
\begin{equation*}
I_3(\log P)^{\sigma_k} \ll P\max_{2\leqslant t\leqslant P/(\log P)^{\sigma_k}}|G(t)|.
\end{equation*}Similarly, we deduce from (4.2) that
 \begin{equation*}
I_4(\log P)^{\sigma_k} \ll \int_{P/(\log P)^{\sigma_k}}^P |G(t)| {\,{\rm d}} t \leqslant P\max_{2\leqslant t\leqslant P}|G(t)|.
\end{equation*}
\begin{equation*}
I_4(\log P)^{\sigma_k} \ll \int_{P/(\log P)^{\sigma_k}}^P |G(t)| {\,{\rm d}} t \leqslant P\max_{2\leqslant t\leqslant P}|G(t)|.
\end{equation*}Combining these estimates completes the proof.
The above two lemmas suffice to handle ‘minor arc’ behaviour. As is typical in applications of the circle method, we treat the major arcs by establishing asymptotic formulae for the exponential sums (4.1).
Lemma 4.3. (General major arc asymptotic)
Let ![]() $f(y)\in\mathbb{Z}[y]$ have degree k, and let
$f(y)\in\mathbb{Z}[y]$ have degree k, and let ![]() $G:(1,\infty)\to \mathbb{R}$ be a continuously differentiable function. Let
$G:(1,\infty)\to \mathbb{R}$ be a continuously differentiable function. Let ![]() $b \in \mathbb{Z}$ and
$b \in \mathbb{Z}$ and ![]() $m \in \mathbb{N}$ be coprime, and let
$m \in \mathbb{N}$ be coprime, and let ![]() $Q \in \mathbb{N}$ with
$Q \in \mathbb{N}$ with
 \begin{equation}
\frac{f(b+mx) - f(b)}{Q} \in \mathbb{Z}[x].
\end{equation}
\begin{equation}
\frac{f(b+mx) - f(b)}{Q} \in \mathbb{Z}[x].
\end{equation} Let ![]() ${\theta} \in \mathbb{R}$ and
${\theta} \in \mathbb{R}$ and ![]() $P \geqslant 2$, and suppose
$P \geqslant 2$, and suppose ![]() $(q,a) \in \mathbb{N} \times \mathbb{Z}$ with
$(q,a) \in \mathbb{N} \times \mathbb{Z}$ with ![]() $(a,q) = 1$ and
$(a,q) = 1$ and
 \begin{equation*}
q \ll (\log P)^{2 C_k},
\qquad
|q \theta - a| \ll \frac{Q (\log P)^{2C_k}}{P^k}.
\end{equation*}
\begin{equation*}
q \ll (\log P)^{2 C_k},
\qquad
|q \theta - a| \ll \frac{Q (\log P)^{2C_k}}{P^k}.
\end{equation*} Let c > 0 be constant, small in terms of Ck, and put ![]() ${\beta} = \theta - a/q$. If P is sufficiently large relative to m and Q, then
${\beta} = \theta - a/q$. If P is sufficiently large relative to m and Q, then
 \begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e_Q (
{\theta} f(p)) G(p)\log p = I_{f,G}({\beta}) \frac{S(q,a;m)}{\varphi(mq)} +
O_f(Pe^{-c \sqrt{\log P}}
\lVert G\rVert_{\mathcal S[2,P]}),
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e_Q (
{\theta} f(p)) G(p)\log p = I_{f,G}({\beta}) \frac{S(q,a;m)}{\varphi(mq)} +
O_f(Pe^{-c \sqrt{\log P}}
\lVert G\rVert_{\mathcal S[2,P]}),
\end{equation*}where
 \begin{equation*}
I_{f,G}({\beta}) = \int_2^P e_Q
({\beta} f(t)) G(t) {\,{\rm d}} t,
\qquad
S(q,a; m) = \sum_{\substack{t \;(\operatorname{mod}{mq}) \\ (t,q) = 1 \\ t \equiv b \;(\operatorname{mod}{m})}} e_{Qq} (af(t)).
\end{equation*}
\begin{equation*}
I_{f,G}({\beta}) = \int_2^P e_Q
({\beta} f(t)) G(t) {\,{\rm d}} t,
\qquad
S(q,a; m) = \sum_{\substack{t \;(\operatorname{mod}{mq}) \\ (t,q) = 1 \\ t \equiv b \;(\operatorname{mod}{m})}} e_{Qq} (af(t)).
\end{equation*}Remark 4.4. The condition (4.3) holds if ![]() $f(b+mx)/Q \in \mathbb{Z}[x]$.
$f(b+mx)/Q \in \mathbb{Z}[x]$.
Proof. Writing ![]() $g(x)\in\mathbb{Z}[x]$ for the integer polynomial appearing in (4.3), if
$g(x)\in\mathbb{Z}[x]$ for the integer polynomial appearing in (4.3), if ![]() $u \in \mathbb{Z}$, then
$u \in \mathbb{Z}$, then
 \begin{equation*}
\frac{f(b+m(u + qv)) - f(b)}{Qq} - \frac{g(u)}{q} = \frac{g(u+qv) - g(u)}{q} \in\mathbb{Z}[v].
\end{equation*}
\begin{equation*}
\frac{f(b+m(u + qv)) - f(b)}{Qq} - \frac{g(u)}{q} = \frac{g(u+qv) - g(u)}{q} \in\mathbb{Z}[v].
\end{equation*}This implies that
Hence, for ![]() $n \leqslant P$,
$n \leqslant P$,
 \begin{equation*}
S_n := \sum_{\substack{p \leqslant n \\ p \equiv b \;(\operatorname{mod}{m})}} e_{Qq}(
af(p))
= O(mq) +
\sum_{\substack{t \;(\operatorname{mod}{mq}) \\ (t,q) = 1 \\ t \equiv b \;(\operatorname{mod}{m})}} e_{Qq} \left(a f(t)\right)
\sum_{\substack{p \leqslant n \\
p \equiv t \;(\operatorname{mod}{mq})}} 1.
\end{equation*}
\begin{equation*}
S_n := \sum_{\substack{p \leqslant n \\ p \equiv b \;(\operatorname{mod}{m})}} e_{Qq}(
af(p))
= O(mq) +
\sum_{\substack{t \;(\operatorname{mod}{mq}) \\ (t,q) = 1 \\ t \equiv b \;(\operatorname{mod}{m})}} e_{Qq} \left(a f(t)\right)
\sum_{\substack{p \leqslant n \\
p \equiv t \;(\operatorname{mod}{mq})}} 1.
\end{equation*}By the Siegel–Walfisz theorem (theorem 2.1), the inner sum is
 \begin{equation*}
\sum_{\substack{p \leqslant n \\
p \equiv t \;(\operatorname{mod}{mq})}} 1
= \frac{{\mathrm{Li}}(n)}{\varphi(mq)}
+ O(Pe^{-3c \sqrt{\log P}}),
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant n \\
p \equiv t \;(\operatorname{mod}{mq})}} 1
= \frac{{\mathrm{Li}}(n)}{\varphi(mq)}
+ O(Pe^{-3c \sqrt{\log P}}),
\end{equation*}whence
 \begin{equation*}
S_n = \frac{{\mathrm{Li}}(n)}{\varphi(mq)} S(q,a;m) + O(P e^{-2c \sqrt{\log P}}).
\end{equation*}
\begin{equation*}
S_n = \frac{{\mathrm{Li}}(n)}{\varphi(mq)} S(q,a;m) + O(P e^{-2c \sqrt{\log P}}).
\end{equation*} Writing ![]() $\psi(t) = e_Q({\beta} f(t)) G(t)\log t$, summation by parts gives
$\psi(t) = e_Q({\beta} f(t)) G(t)\log t$, summation by parts gives
 \begin{align*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e_Q\left(
F(p) \right) G(p) \log p &= \sum_{n \leqslant P} (S_n - S_{n-1}) \psi(n)
\\ &= S_P \psi(P+1) + \sum_{n \leqslant P} S_n (\psi(n) - \psi(n+1)).
\end{align*}
\begin{align*}
\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e_Q\left(
F(p) \right) G(p) \log p &= \sum_{n \leqslant P} (S_n - S_{n-1}) \psi(n)
\\ &= S_P \psi(P+1) + \sum_{n \leqslant P} S_n (\psi(n) - \psi(n+1)).
\end{align*}By hypothesis, for P sufficiently large,
 \begin{equation*}
|\beta| =
|\theta - a/q| \ll \frac{Q(\log P)^{2C_k}}{qP^k} \ll \frac{(\log P)^{2C_k+1}}{P^k}.
\end{equation*}
\begin{equation*}
|\beta| =
|\theta - a/q| \ll \frac{Q(\log P)^{2C_k}}{qP^k} \ll \frac{(\log P)^{2C_k+1}}{P^k}.
\end{equation*} Hence, for all ![]() $x,y\in[2,P]$ with x < y, the mean value theorem yields
$x,y\in[2,P]$ with x < y, the mean value theorem yields
 \begin{align*}
\notag
\left\lvert\frac{\psi(y) - \psi(x)}{y-x}\right\rvert
&\leqslant \sup_{t\in[x,y]}\left\lbrace |G(t)/t| + |G'(t)\log t|+ |\beta f'(t)G(t)\log t| \right\rbrace
\end{align*}
\begin{align*}
\notag
\left\lvert\frac{\psi(y) - \psi(x)}{y-x}\right\rvert
&\leqslant \sup_{t\in[x,y]}\left\lbrace |G(t)/t| + |G'(t)\log t|+ |\beta f'(t)G(t)\log t| \right\rbrace
\end{align*} \begin{align}
&\ll_f \lVert G\rVert_{L^{\infty}[2,P]}\left(\frac{1}{x} + \frac{(\log P)^{2(C_k + 1)}}{P}\right) + \lVert G'\rVert_{L^{\infty}[2,P]}\log P.
\end{align}
\begin{align}
&\ll_f \lVert G\rVert_{L^{\infty}[2,P]}\left(\frac{1}{x} + \frac{(\log P)^{2(C_k + 1)}}{P}\right) + \lVert G'\rVert_{L^{\infty}[2,P]}\log P.
\end{align}In particular, this shows that
 \begin{align*}
\sum_{n \leqslant P} |\psi(n) - \psi(n+1)| &\ll \lVert G\rVert_{L^{\infty}[2,P]}\left((\log P)^{2(C_k + 1)}+ \sum_{n\leqslant P} \frac{1}{n}\right)
\\ &\quad + \lVert G'\rVert_{L^{\infty}[2,P]}P\log P
\\ &\ll (\log P)^{2(C_k+1)}\lVert G\rVert_{\mathcal S[2,P]}.
\end{align*}
\begin{align*}
\sum_{n \leqslant P} |\psi(n) - \psi(n+1)| &\ll \lVert G\rVert_{L^{\infty}[2,P]}\left((\log P)^{2(C_k + 1)}+ \sum_{n\leqslant P} \frac{1}{n}\right)
\\ &\quad + \lVert G'\rVert_{L^{\infty}[2,P]}P\log P
\\ &\ll (\log P)^{2(C_k+1)}\lVert G\rVert_{\mathcal S[2,P]}.
\end{align*} As  ${\mathrm{Li}}(t) = \sum_{n=3}^t \int_{n-1}^n \frac{{\,{\rm d}} x}{\log x}$, summation by parts now gives
${\mathrm{Li}}(t) = \sum_{n=3}^t \int_{n-1}^n \frac{{\,{\rm d}} x}{\log x}$, summation by parts now gives
 \begin{align*}
&\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e_Q\left(
F(p) \right) G(p) \log p + O(P e^{-c \sqrt{\log P}}\lVert G\rVert_{\mathcal S[2,P]}) \\
&= \frac{S(q,a;m)}{\varphi(mq)}
\left( {\mathrm{Li}}(P)\psi(P+1) +
\sum_{n \leqslant P} {\mathrm{Li}}(n) (\psi(n) - \psi(n+1))
\right)
\\
&= \frac{S(q,a;m)}{\varphi(mq)}
\sum_{3 \leqslant n \leqslant P}
\int_{n-1}^n \frac{\psi(n)}{\log x} {\,{\rm d}} x.
\end{align*}
\begin{align*}
&\sum_{\substack{p \leqslant P \\ p \equiv b \;(\operatorname{mod}{m})}} e_Q\left(
F(p) \right) G(p) \log p + O(P e^{-c \sqrt{\log P}}\lVert G\rVert_{\mathcal S[2,P]}) \\
&= \frac{S(q,a;m)}{\varphi(mq)}
\left( {\mathrm{Li}}(P)\psi(P+1) +
\sum_{n \leqslant P} {\mathrm{Li}}(n) (\psi(n) - \psi(n+1))
\right)
\\
&= \frac{S(q,a;m)}{\varphi(mq)}
\sum_{3 \leqslant n \leqslant P}
\int_{n-1}^n \frac{\psi(n)}{\log x} {\,{\rm d}} x.
\end{align*}Note that
 \begin{equation*}
\sum_{3 \leqslant n \leqslant P}
\int_{n-1}^{n}
\frac{{\,{\rm d}} x}
{(n-1)\log x}
\ll \sum_{3 \leqslant n \leqslant P}
\int_{n-1}^{n}
\frac{{\,{\rm d}} x}
{x\log x} = \log \log P - \log \log 2.
\end{equation*}
\begin{equation*}
\sum_{3 \leqslant n \leqslant P}
\int_{n-1}^{n}
\frac{{\,{\rm d}} x}
{(n-1)\log x}
\ll \sum_{3 \leqslant n \leqslant P}
\int_{n-1}^{n}
\frac{{\,{\rm d}} x}
{x\log x} = \log \log P - \log \log 2.
\end{equation*} Thus, using (4.4) to replace each ![]() $\psi(n)$ by
$\psi(n)$ by ![]() $\psi(x)$, we obtain
$\psi(x)$, we obtain
 \begin{align*}
\sum_{3 \leqslant n \leqslant P}
\int_{n-1}^n \frac{\psi(n)}{\log x} {\,{\rm d}} x
&= I_{f,G}({\beta}) + O((\log P)^{2(C_k+1)}\lVert G\rVert_{\mathcal S[2,P]}),
\end{align*}
\begin{align*}
\sum_{3 \leqslant n \leqslant P}
\int_{n-1}^n \frac{\psi(n)}{\log x} {\,{\rm d}} x
&= I_{f,G}({\beta}) + O((\log P)^{2(C_k+1)}\lVert G\rVert_{\mathcal S[2,P]}),
\end{align*}which completes the proof.
5. Fourier decay
Returning to the study of our weight function ν, we need to show that it is suitably ‘pseudorandom’. This will then allow us to ‘transfer’ solutions from the linearized equation (2.7) to our original equation (2.6). As in [Reference Chapman and Chow2, Reference Chow4, Reference Chow, Lindqvist and Prendiville5, Reference Prendiville17], we accomplish this via a Fourier decay estimate (together with the restriction estimates from the next section).
Lemma 5.1. Let ν be as defined in (3.2), where ![]() $b\in[W\kappa]$ satisfies (3.1), and assume that X is sufficiently large in terms of w. Then, for all
$b\in[W\kappa]$ satisfies (3.1), and assume that X is sufficiently large in terms of w. Then, for all ![]() $\alpha\in\mathbb{T}$,
$\alpha\in\mathbb{T}$,
 \begin{equation}
|\hat \nu({\alpha}) -
\widehat{1_{[N]}} ({\alpha})|
\ll_{h,\varepsilon} w^{\varepsilon-1/d} N.
\end{equation}
\begin{equation}
|\hat \nu({\alpha}) -
\widehat{1_{[N]}} ({\alpha})|
\ll_{h,\varepsilon} w^{\varepsilon-1/d} N.
\end{equation}Remark 5.2. As in [Reference Chapman and Chow2, §5], the above lemma does not rely upon nor make any reference to sets ![]() $A\subseteq\mathcal P_X$ or
$A\subseteq\mathcal P_X$ or ![]() $\mathcal A\subseteq[N]$.
$\mathcal A\subseteq[N]$.
We study the Fourier transform ![]() $\hat{\nu}$ using the Hardy–Littlewood circle method and the exponential sum estimates established previously. We define the set of minor arcs
$\hat{\nu}$ using the Hardy–Littlewood circle method and the exponential sum estimates established previously. We define the set of minor arcs
 \begin{equation*}
\mathfrak m :=\left\lbrace\alpha\in\mathbb{T} : \max \{q, X^d \| q {\alpha} \| \} \gt (\log X)^{2C_d} \text{for all } q\in\mathbb{N}\right\rbrace.
\end{equation*}
\begin{equation*}
\mathfrak m :=\left\lbrace\alpha\in\mathbb{T} : \max \{q, X^d \| q {\alpha} \| \} \gt (\log X)^{2C_d} \text{for all } q\in\mathbb{N}\right\rbrace.
\end{equation*} The set of major arcs ![]() $\mathfrak M:=\mathbb{T}\setminus\mathfrak m$, therefore, consists of all
$\mathfrak M:=\mathbb{T}\setminus\mathfrak m$, therefore, consists of all ![]() $\alpha\in\mathbb{T}$ for which there exist
$\alpha\in\mathbb{T}$ for which there exist ![]() $a,q\in\mathbb{Z}$ such that
$a,q\in\mathbb{Z}$ such that
For convenience, we recall that
 \begin{equation*}
\hat \nu({\alpha}) =
\frac{\varphi(W)}{W(h'(b),W)}
\sum_{\substack{
b \lt p \leqslant X \\
p \equiv b \;(\operatorname{mod}{W {\kappa}})}}
h'(p) \log p \cdot e \left(
{\alpha} \frac{h(p)-h(b)}
{{\lambda}(D)} \right) \quad (\alpha\in\mathbb{T}).
\end{equation*}
\begin{equation*}
\hat \nu({\alpha}) =
\frac{\varphi(W)}{W(h'(b),W)}
\sum_{\substack{
b \lt p \leqslant X \\
p \equiv b \;(\operatorname{mod}{W {\kappa}})}}
h'(p) \log p \cdot e \left(
{\alpha} \frac{h(p)-h(b)}
{{\lambda}(D)} \right) \quad (\alpha\in\mathbb{T}).
\end{equation*} We, therefore, observe that the results of the previous section may be applied to estimate ![]() $\hat \nu({\alpha})$ upon taking
$\hat \nu({\alpha})$ upon taking
With this choice of parameters, we compute that
 \begin{equation}
\lVert G\rVert_{\mathcal S[2,P]} \ll_h X^{d-1}
\end{equation}
\begin{equation}
\lVert G\rVert_{\mathcal S[2,P]} \ll_h X^{d-1}
\end{equation}and
 \begin{equation}
I_{f,G}(\beta)
= \int_2^X e({\beta} h(x)/{\lambda}(D)) h'(x) {\,{\rm d}} x
= {\lambda}(D)\left( O_h(1) + \int_{0}^{N} e({\beta} y){\,{\rm d}} y\right).
\end{equation}
\begin{equation}
I_{f,G}(\beta)
= \int_2^X e({\beta} h(x)/{\lambda}(D)) h'(x) {\,{\rm d}} x
= {\lambda}(D)\left( O_h(1) + \int_{0}^{N} e({\beta} y){\,{\rm d}} y\right).
\end{equation} Our proof of lemma 5.1 for ![]() $\alpha\in\mathfrak m$ proceeds by the same strategy as in [Reference Chow4, §4]: we show that
$\alpha\in\mathfrak m$ proceeds by the same strategy as in [Reference Chow4, §4]: we show that ![]() $\hat{\nu}(\alpha)$ and
$\hat{\nu}(\alpha)$ and  $\hat{1}_{[N]}(\alpha)$ are both far smaller than the required upper bound. This is encapsulated in the following corollary of lemma 4.2.
$\hat{1}_{[N]}(\alpha)$ are both far smaller than the required upper bound. This is encapsulated in the following corollary of lemma 4.2.
Corollary 5.3. (Minor arc estimate)
If ![]() $\alpha\in\mathfrak m$, then
$\alpha\in\mathfrak m$, then
 \begin{equation*}
\hat{\nu}(\alpha) \ll_{h} X^d(\log X)^{-\sigma_d} \qquad \text{and} \qquad \widehat{1_{[N]}} ({\alpha}) \ll X^d(\log X)^{-2C_d}.
\end{equation*}
\begin{equation*}
\hat{\nu}(\alpha) \ll_{h} X^d(\log X)^{-\sigma_d} \qquad \text{and} \qquad \widehat{1_{[N]}} ({\alpha}) \ll X^d(\log X)^{-2C_d}.
\end{equation*}Proof. In view of (5.3) and (5.4), the first estimate follows immediately from lemma 4.2. For the second estimate, we deduce from the definition of ![]() $\mathfrak m$ that
$\mathfrak m$ that
 \begin{equation*}
\widehat{1_{[N]}} ({\alpha}) = \sum_{n=1}^{N}e(\alpha n) \ll \lVert\alpha\rVert^{-1} \leqslant X^d(\log X)^{-2C_d} \qquad (\alpha\in\mathfrak m),
\end{equation*}
\begin{equation*}
\widehat{1_{[N]}} ({\alpha}) = \sum_{n=1}^{N}e(\alpha n) \ll \lVert\alpha\rVert^{-1} \leqslant X^d(\log X)^{-2C_d} \qquad (\alpha\in\mathfrak m),
\end{equation*}as required.
We similarly establish an asymptotic formula for ![]() $\hat{\nu}(\alpha)$ on the major arcs by invoking lemma 4.3. Define
$\hat{\nu}(\alpha)$ on the major arcs by invoking lemma 4.3. Define
 \begin{equation*}
S(q,a) := \sum_{\substack{t \;(\operatorname{mod}{W {\kappa} q}) \\ (t,q) = 1 \\ t \equiv b \;(\operatorname{mod}{W {\kappa}})}} e_q \left(
a \frac{h(t) - h(b)}{{\lambda}(D)} \right), \qquad I({\beta}) :=
\int_0^N e({\beta} y) {\,{\rm d}} y.
\end{equation*}
\begin{equation*}
S(q,a) := \sum_{\substack{t \;(\operatorname{mod}{W {\kappa} q}) \\ (t,q) = 1 \\ t \equiv b \;(\operatorname{mod}{W {\kappa}})}} e_q \left(
a \frac{h(t) - h(b)}{{\lambda}(D)} \right), \qquad I({\beta}) :=
\int_0^N e({\beta} y) {\,{\rm d}} y.
\end{equation*}Corollary 5.4. (Major arc asymptotic)
Suppose ![]() $({\alpha},q,a) \in \mathbb{R} \times \mathbb{N} \times \mathbb{Z}$ with (5.2), and put
$({\alpha},q,a) \in \mathbb{R} \times \mathbb{N} \times \mathbb{Z}$ with (5.2), and put ![]() ${\beta} = {\alpha} - a/q$. Let c > 0 be constant, small in terms of Cd. Then,
${\beta} = {\alpha} - a/q$. Let c > 0 be constant, small in terms of Cd. Then,
 \begin{equation*}
\hat \nu({\alpha}) = \frac{\varphi(W{\kappa})}{\varphi(W{\kappa} q)}
S(q,a) I({\beta})
+ O_h(Ne^{-c \sqrt{\log X}}).
\end{equation*}
\begin{equation*}
\hat \nu({\alpha}) = \frac{\varphi(W{\kappa})}{\varphi(W{\kappa} q)}
S(q,a) I({\beta})
+ O_h(Ne^{-c \sqrt{\log X}}).
\end{equation*}Proof. Recall that ![]() $\lambda(D)N = h(X)\asymp_h X^d$. Thus, by combining (5.3) with (5.4) and (5.5), the desired formula is provided by lemma 4.3.
$\lambda(D)N = h(X)\asymp_h X^d$. Thus, by combining (5.3) with (5.4) and (5.5), the desired formula is provided by lemma 4.3.
To elucidate this formula further, we estimate ![]() $S(q,a)$.
$S(q,a)$.
Lemma 5.5. Let ![]() $a,q\in\mathbb{Z}$ with
$a,q\in\mathbb{Z}$ with ![]() $q \geqslant 2$ and
$q \geqslant 2$ and ![]() $(q,a) = 1$. Then,
$(q,a) = 1$. Then,
 \begin{equation*}
S(q,a) \ll_{h,\varepsilon} \min\left\lbrace q^{\varepsilon - 1/d}\varphi(q),\; \frac{\varphi(W{\kappa} q)}
{\varphi(W {\kappa})}w^{\varepsilon-1/d}\right\rbrace.
\end{equation*}
\begin{equation*}
S(q,a) \ll_{h,\varepsilon} \min\left\lbrace q^{\varepsilon - 1/d}\varphi(q),\; \frac{\varphi(W{\kappa} q)}
{\varphi(W {\kappa})}w^{\varepsilon-1/d}\right\rbrace.
\end{equation*} Furthermore, if ![]() $(q,W) \gt 1$, then
$(q,W) \gt 1$, then ![]() $S(q,a) = 0$.
$S(q,a) = 0$.
Proof. Write ![]() $q = q_1q_2$, where
$q = q_1q_2$, where ![]() $q_1 \in \mathbb{N}$ is w-smooth and q 2 is w-rough. Observe that
$q_1 \in \mathbb{N}$ is w-smooth and q 2 is w-rough. Observe that
 \begin{equation*}
S(q,a) = \sum_{\substack{
x \;(\operatorname{mod}{q}) \\
(W{\kappa} x + b, q) = 1}}
e_q(ag(x)),
\end{equation*}
\begin{equation*}
S(q,a) = \sum_{\substack{
x \;(\operatorname{mod}{q}) \\
(W{\kappa} x + b, q) = 1}}
e_q(ag(x)),
\end{equation*}where
 \begin{equation*}
g(x) = \frac{h(W {\kappa} x + b) - h(b)}{{\lambda}(D)} =
\frac{h(W {\kappa} x + b) - h(b)}{W{\kappa} (h'(b), W{\kappa})}
\in \mathbb{Z}[x]
\end{equation*}
\begin{equation*}
g(x) = \frac{h(W {\kappa} x + b) - h(b)}{{\lambda}(D)} =
\frac{h(W {\kappa} x + b) - h(b)}{W{\kappa} (h'(b), W{\kappa})}
\in \mathbb{Z}[x]
\end{equation*} by Taylor’s theorem. As ![]() $(q_1,q_2)
= 1$, a standard calculation reveals that
$(q_1,q_2)
= 1$, a standard calculation reveals that
where
 \begin{equation*}
\frac{a}{q} = \frac{A_1}{q_1} + \frac{A_2}{q_2},
\end{equation*}
\begin{equation*}
\frac{a}{q} = \frac{A_1}{q_1} + \frac{A_2}{q_2},
\end{equation*} as is noted in the proof of [Reference Rice19, lemma 9]. Observe that ![]() $(A_1,q_1) = (A_2,q_2) = 1$.
$(A_1,q_1) = (A_2,q_2) = 1$.
As q 1 is w-smooth and ![]() $(b,W)=1$, we always have
$(b,W)=1$, we always have ![]() $(W{\kappa} x+b, q_1) = 1$. Let
$(W{\kappa} x+b, q_1) = 1$. Let
so that ![]() $(q_1',W') = 1$. Writing
$(q_1',W') = 1$. Writing ![]() $x = y + q_1'z$ and
$x = y + q_1'z$ and
gives
 \begin{align*}
S(q_1,A_1) &=
\sum_{y \;(\operatorname{mod}{q_1'})} \:
\sum_{z \;(\operatorname{mod}{H})}
e_{Hq_1'}(A_1 \sum_{j \leqslant d}
v_j (y + q_1'z)^j).
\end{align*}
\begin{align*}
S(q_1,A_1) &=
\sum_{y \;(\operatorname{mod}{q_1'})} \:
\sum_{z \;(\operatorname{mod}{H})}
e_{Hq_1'}(A_1 \sum_{j \leqslant d}
v_j (y + q_1'z)^j).
\end{align*}As
we must have ![]() $(h'(b),W) \mid V \mid {\kappa}$. Thus, for
$(h'(b),W) \mid V \mid {\kappa}$. Thus, for ![]() $2 \leqslant j \leqslant d$, we have
$2 \leqslant j \leqslant d$, we have
 \begin{equation*}
v_j = \frac{h^{(j)}(b)
(W {\kappa})^{j-1}}
{j! (h'(b),W)} \equiv 0 \;(\operatorname{mod}{W}).
\end{equation*}
\begin{equation*}
v_j = \frac{h^{(j)}(b)
(W {\kappa})^{j-1}}
{j! (h'(b),W)} \equiv 0 \;(\operatorname{mod}{W}).
\end{equation*}Now
 \begin{equation*}
S(q_1,A_1) = \sum_{y \leqslant q'_1} e_{q_1} (A_1 g(y))
\sum_{z \leqslant H}
e_H(A_1 v_1 z),
\qquad
v_1 = \frac{h'(b)}{(h'(b),W)}.
\end{equation*}
\begin{equation*}
S(q_1,A_1) = \sum_{y \leqslant q'_1} e_{q_1} (A_1 g(y))
\sum_{z \leqslant H}
e_H(A_1 v_1 z),
\qquad
v_1 = \frac{h'(b)}{(h'(b),W)}.
\end{equation*} For each prime ![]() $p \leqslant w$, we have
$p \leqslant w$, we have ![]() $\mathrm{ord}_p(h'(b)) \lt \mathrm{ord}_p(W)$, and so
$\mathrm{ord}_p(h'(b)) \lt \mathrm{ord}_p(W)$, and so ![]() $\mathrm{ord}_p(v_1) = 0$. Therefore,
$\mathrm{ord}_p(v_1) = 0$. Therefore, ![]() $(v_1,W) = 1$, so
$(v_1,W) = 1$, so ![]() $(H, A_1 v_1 ) =1$, whence
$(H, A_1 v_1 ) =1$, whence
 \begin{equation*}
S(q_1,A_1) = \begin{cases}
1, &\text{if } q_1 = 1 \\
0, &\text{if } q_1 \geqslant 2.
\end{cases}
\end{equation*}
\begin{equation*}
S(q_1,A_1) = \begin{cases}
1, &\text{if } q_1 = 1 \\
0, &\text{if } q_1 \geqslant 2.
\end{cases}
\end{equation*} This completes the proof of the assertion that ![]() $S(q,a)=0$ whenever
$S(q,a)=0$ whenever ![]() $(q,W) \gt 1$.
$(q,W) \gt 1$.
In view of this result, we may henceforth assume that ![]() $q_1=1$ and
$q_1=1$ and ![]() $q_2 = q \geqslant 2$. In particular, we have q > w. Let us denote by
$q_2 = q \geqslant 2$. In particular, we have q > w. Let us denote by ![]() $\ell_h$ the leading coefficient of h. Then
$\ell_h$ the leading coefficient of h. Then
 \begin{equation*}
v_d = \frac{\ell_h (W {\kappa})^{d-1}} {(h'(b),W)},
\qquad (q,W) = 1,
\end{equation*}
\begin{equation*}
v_d = \frac{\ell_h (W {\kappa})^{d-1}} {(h'(b),W)},
\qquad (q,W) = 1,
\end{equation*} so ![]() $(v_d, q) \ll_h 1$. Now lemma 2.2 provides a constant
$(v_d, q) \ll_h 1$. Now lemma 2.2 provides a constant ![]() $C=C(d) \gt 1$ such that
$C=C(d) \gt 1$ such that
 \begin{equation*}
S(q,a) = S(q, A_2) \ll_h
C^{{\omega}(q)} q^{1-1/d}
\ll_{d,\varepsilon} q^{\varepsilon - 1/d} \varphi(q) \lt \frac{\varphi(W{\kappa} q)}{\varphi(W {\kappa})} w^{\varepsilon-1/d},
\end{equation*}
\begin{equation*}
S(q,a) = S(q, A_2) \ll_h
C^{{\omega}(q)} q^{1-1/d}
\ll_{d,\varepsilon} q^{\varepsilon - 1/d} \varphi(q) \lt \frac{\varphi(W{\kappa} q)}{\varphi(W {\kappa})} w^{\varepsilon-1/d},
\end{equation*}as required.
These two results allow us to establish our Fourier decay estimate.
Proof of lemma 5.1
Corollary 5.3 gives (5.1) for all ![]() $\alpha\in\mathfrak m$. We henceforth assume that
$\alpha\in\mathfrak m$. We henceforth assume that ![]() $\alpha\in\mathfrak M$. We begin by considering the case where (5.2) holds with q = 1. As demonstrated in [Reference Chow4, § 4], Euler–Maclaurin summation delivers the bound
$\alpha\in\mathfrak M$. We begin by considering the case where (5.2) holds with q = 1. As demonstrated in [Reference Chow4, § 4], Euler–Maclaurin summation delivers the bound
 \begin{equation*}
\widehat{1_{[N]}} ({\alpha})
- I(\alpha) \ll_h
(\log X)^{2C_d}.
\end{equation*}
\begin{equation*}
\widehat{1_{[N]}} ({\alpha})
- I(\alpha) \ll_h
(\log X)^{2C_d}.
\end{equation*}Applying the triangle inequality and corollary 5.4, therefore, gives
 \begin{equation*}
|\hat{\nu}(\alpha) - \widehat{1_{[N]}} ({\alpha})| \leqslant |\hat{\nu}(\alpha) - I(\alpha)| + |\widehat{1_{[N]}} ({\alpha}) -I(\alpha)| \ll_h Ne^{-c\sqrt{\log X}}.
\end{equation*}
\begin{equation*}
|\hat{\nu}(\alpha) - \widehat{1_{[N]}} ({\alpha})| \leqslant |\hat{\nu}(\alpha) - I(\alpha)| + |\widehat{1_{[N]}} ({\alpha}) -I(\alpha)| \ll_h Ne^{-c\sqrt{\log X}}.
\end{equation*} Finally, suppose that (5.2) holds with ![]() $q \geqslant 2$. We note from [Reference Chow4, equation (4.3)] that
$q \geqslant 2$. We note from [Reference Chow4, equation (4.3)] that
 \begin{equation*}
\widehat{1_{[N]}} ({\alpha})
\ll q \leqslant (\log X)^{2 C_d}.
\end{equation*}
\begin{equation*}
\widehat{1_{[N]}} ({\alpha})
\ll q \leqslant (\log X)^{2 C_d}.
\end{equation*} Thus, in view of the trivial estimate ![]() $|I({\beta})| \leqslant N$, the desired result follows by combining corollary 5.4 with lemma 5.5.
$|I({\beta})| \leqslant N$, the desired result follows by combining corollary 5.4 with lemma 5.5.
Before moving on, we record the following consequence of corollary 5.4 and lemma 5.5, which we use in the next section.
Corollary 5.6. (Major arc estimate)
Let ![]() $\alpha\in\mathbb{T}$ and
$\alpha\in\mathbb{T}$ and ![]() $q\in\mathbb{N}$. If (5.2) holds for some
$q\in\mathbb{N}$. If (5.2) holds for some ![]() $a \in \mathbb{Z}$, then
$a \in \mathbb{Z}$, then
 \begin{equation*}
\hat \nu({\alpha})
\ll_{h,\varepsilon} q^{\varepsilon - 1/d}
\min \{N, \| {\alpha} - a/q \|^{-1} \} +
O(Ne^{-c \sqrt{\log X}}).
\end{equation*}
\begin{equation*}
\hat \nu({\alpha})
\ll_{h,\varepsilon} q^{\varepsilon - 1/d}
\min \{N, \| {\alpha} - a/q \|^{-1} \} +
O(Ne^{-c \sqrt{\log X}}).
\end{equation*}Proof. Integrating by parts delivers the standard estimate
Incorporating the elementary inequality ![]() $\varphi(W\kappa)\varphi(q)\leqslant\varphi(W\kappa q)$ and lemma 5.5 delivers
$\varphi(W\kappa)\varphi(q)\leqslant\varphi(W\kappa q)$ and lemma 5.5 delivers
 \begin{equation*}
\frac{\varphi(W\kappa)}{\varphi(W\kappa q)}S(q,a)I({\alpha} - a/q) \ll_{h,\varepsilon} q^{\varepsilon-1/d}
\min \{N,\| {\alpha} - a/q \|^{-1} \}.
\end{equation*}
\begin{equation*}
\frac{\varphi(W\kappa)}{\varphi(W\kappa q)}S(q,a)I({\alpha} - a/q) \ll_{h,\varepsilon} q^{\varepsilon-1/d}
\min \{N,\| {\alpha} - a/q \|^{-1} \}.
\end{equation*}The required result now follows from corollary 5.4.
6. Restriction estimates
Recall from §3 that ν is supported on the set
 \begin{equation*}
\left \{n\in[N]: n=\frac{h(p) - h(b)}{{\lambda}(D)},\; p\in\mathcal P_X,\; p\equiv b \;(\operatorname{mod}{W\kappa}) \right \}.
\end{equation*}
\begin{equation*}
\left \{n\in[N]: n=\frac{h(p) - h(b)}{{\lambda}(D)},\; p\in\mathcal P_X,\; p\equiv b \;(\operatorname{mod}{W\kappa}) \right \}.
\end{equation*} After linearizing, we wish to solve (2.7) with the ni drawn from a dense subset ![]() $\mathcal A$ of the above set. This leads us to the study of functions
$\mathcal A$ of the above set. This leads us to the study of functions ![]() $\phi:\mathbb{Z}\to\mathbb{C}$, such as the indicator function of
$\phi:\mathbb{Z}\to\mathbb{C}$, such as the indicator function of ![]() $1_{\mathcal A}$, which are majorized by ν, meaning that
$1_{\mathcal A}$, which are majorized by ν, meaning that ![]() $|\phi|\leqslant\nu$.
$|\phi|\leqslant\nu$.
The purpose of this section is to establish two restriction estimates. These will then be used in the next section to execute the transference argument. The first restriction estimate is for the weight ν and is needed to transfer between ‘dense variables’ xi and ni in equations (2.6) and (2.7), respectively. Our second restriction estimate concerns an auxiliary weight function νD and is required for interpolation.
Throughout this section, we define ν as in §3.2 for a fixed choice of ![]() $b\in[W\kappa]$ satisfying (3.1). We also let
$b\in[W\kappa]$ satisfying (3.1). We also let ![]() $T = T(d)$ be as in §2.
$T = T(d)$ be as in §2.
6.1. Restriction I
We begin with the following restriction estimate for ν.
Proposition 6.1. Let ![]() $E \gt 2T$, and let
$E \gt 2T$, and let ![]() $\phi: \mathbb{Z} \to \mathbb{C}$ with
$\phi: \mathbb{Z} \to \mathbb{C}$ with ![]() $|\phi| \leqslant \nu$. Then,
$|\phi| \leqslant \nu$. Then,
 \begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^E {\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^E {\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*} This is easily bootstrapped to the following restriction estimate for ![]() $\nu + 1_{[N]}$, see the deduction of [Reference Chapman and Chow2, lemma 6.2].
$\nu + 1_{[N]}$, see the deduction of [Reference Chapman and Chow2, lemma 6.2].
Proposition 6.2. Let ![]() $E \gt 2T$, and let
$E \gt 2T$, and let ![]() $\phi: \mathbb{Z} \to \mathbb{C}$ with
$\phi: \mathbb{Z} \to \mathbb{C}$ with ![]() $|\phi| \leqslant \nu + 1_{[N]}$. Then,
$|\phi| \leqslant \nu + 1_{[N]}$. Then,
 \begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^E {\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^E {\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*}To prove proposition 6.1, we proceed in stages. We introduce the auxiliary function
 \begin{equation*}
\mu: \mathbb{Z} \to [0,\infty),
\qquad
\mu(n) = \frac{1}{(h'(b),W)}
\sum_{\substack{
b \lt x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}}) \\
h(x) - h(b) = n {\lambda}(D)}}
h'(x),
\end{equation*}
\begin{equation*}
\mu: \mathbb{Z} \to [0,\infty),
\qquad
\mu(n) = \frac{1}{(h'(b),W)}
\sum_{\substack{
b \lt x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}}) \\
h(x) - h(b) = n {\lambda}(D)}}
h'(x),
\end{equation*} noting that ![]() $\nu \leqslant (\log X) \mu$ pointwise. We compute that
$\nu \leqslant (\log X) \mu$ pointwise. We compute that
 \begin{align*}
\| \mu \|_1 &= (h'(b),W)^{-1}
\sum_{\substack{b \lt x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}} h'(x) \\
&\ll (h'(b),W)^{-1}
\sum_{y \leqslant X/W {\kappa}}
(W {\kappa} y)^{d-1} \\
&\ll \frac{X^d}{W {\kappa} (h'(b),W)}
= \frac{X^d}{{\lambda}(D)}
\ll N.
\end{align*}
\begin{align*}
\| \mu \|_1 &= (h'(b),W)^{-1}
\sum_{\substack{b \lt x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}} h'(x) \\
&\ll (h'(b),W)^{-1}
\sum_{y \leqslant X/W {\kappa}}
(W {\kappa} y)^{d-1} \\
&\ll \frac{X^d}{W {\kappa} (h'(b),W)}
= \frac{X^d}{{\lambda}(D)}
\ll N.
\end{align*}We begin with an epsilon-slack restriction estimate for µ.
Lemma 6.3. (Epsilon-slack estimate)
Let ![]() $\psi: \mathbb{Z} \to \mathbb{C}$ with
$\psi: \mathbb{Z} \to \mathbb{C}$ with ![]() $|\psi| \leqslant \mu$. Then,
$|\psi| \leqslant \mu$. Then,
 \begin{equation*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} \ll_{h,\varepsilon} N^{2T-1+\varepsilon}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} \ll_{h,\varepsilon} N^{2T-1+\varepsilon}.
\end{equation*}Proof. By orthogonality,
 \begin{align*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} = \sum_{n_1 + \cdots + n_T = n_{T+1} + \cdots + n_{2T}} \psi(n_1) \cdots \psi(n_T) \overline{
\psi(n_{T+1}) \cdots
\psi(n_{2T})}.
\end{align*}
\begin{align*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} = \sum_{n_1 + \cdots + n_T = n_{T+1} + \cdots + n_{2T}} \psi(n_1) \cdots \psi(n_T) \overline{
\psi(n_{T+1}) \cdots
\psi(n_{2T})}.
\end{align*} As ![]() $\| \psi \|_\infty \leqslant
\| \mu \|_\infty \ll
X^{d-1}$, and since ψ is supported on
$\| \psi \|_\infty \leqslant
\| \mu \|_\infty \ll
X^{d-1}$, and since ψ is supported on
 \begin{equation*}
\left \{
\frac{h(x) - h(b)}{{\lambda}(D)}: x \in [X] \right \},
\end{equation*}
\begin{equation*}
\left \{
\frac{h(x) - h(b)}{{\lambda}(D)}: x \in [X] \right \},
\end{equation*}we obtain
 \begin{align*}
&\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} \\
&\ll (X^{d-1})^{2T}
\# \{\mathbf{x} \in [X]^{2T}: h(x_1) + \cdots + h(x_T) = h(x_{T+1}) + \cdots + h(x_{2T}) \}.
\end{align*}
\begin{align*}
&\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} \\
&\ll (X^{d-1})^{2T}
\# \{\mathbf{x} \in [X]^{2T}: h(x_1) + \cdots + h(x_T) = h(x_{T+1}) + \cdots + h(x_{2T}) \}.
\end{align*} Finally, using that ![]() $T = T(d)$, we find that
$T = T(d)$, we find that
 \begin{align*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} \ll X^{2T(d-1) + 2T - d + \varepsilon} \ll N^{2T-1+2\varepsilon}.
\end{align*}
\begin{align*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^{2T} {\,{\rm d}} {\alpha} \ll X^{2T(d-1) + 2T - d + \varepsilon} \ll N^{2T-1+2\varepsilon}.
\end{align*}Our next goal is to largely remove ɛ from the exponent in this restriction estimate for µ, obtaining a log-slack estimate by passing to a slightly higher moment. To accomplish this, we require some bounds on
 \begin{equation*}
\hat \mu({\theta}) =
\frac1{(h'(b),W)}
\sum_{\substack{
b \lt x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}}
h'(x)
e\left({\theta} \frac{h(x)-h(b)}{{\lambda}(D)} \right).
\end{equation*}
\begin{equation*}
\hat \mu({\theta}) =
\frac1{(h'(b),W)}
\sum_{\substack{
b \lt x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}}
h'(x)
e\left({\theta} \frac{h(x)-h(b)}{{\lambda}(D)} \right).
\end{equation*}The triangle inequality and partial summation yield
 \begin{equation*}
\hat \mu({\theta})
\ll \frac{X^{d-1}}{(h'(b),W)} \left( 1 +
\max_{X^{1/2} \leqslant P \leqslant X}
|g({\theta};P)| \right),
\end{equation*}
\begin{equation*}
\hat \mu({\theta})
\ll \frac{X^{d-1}}{(h'(b),W)} \left( 1 +
\max_{X^{1/2} \leqslant P \leqslant X}
|g({\theta};P)| \right),
\end{equation*}where
 \begin{equation*}
g({\theta};P) = \frac1{(h'(b),W)}
\sum_{\substack{
b \lt x \leqslant X + b \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}}
e\left({\theta} \frac{h(x)-h(b)}{{\lambda}(D)} \right).
\end{equation*}
\begin{equation*}
g({\theta};P) = \frac1{(h'(b),W)}
\sum_{\substack{
b \lt x \leqslant X + b \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}}
e\left({\theta} \frac{h(x)-h(b)}{{\lambda}(D)} \right).
\end{equation*} Writing ![]() $x = W{\kappa} y + b$ gives
$x = W{\kappa} y + b$ gives
 \begin{equation*}
\sum_{\substack{
x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}} e\left({\theta} \frac{h(x)-h(b)}{{\lambda}(D)} \right)
= \sum_{y \leqslant X/(W{\kappa})}
e\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta} f_d(y)
\right),
\end{equation*}
\begin{equation*}
\sum_{\substack{
x \leqslant X \\
x \equiv b \;(\operatorname{mod}{W {\kappa}})}} e\left({\theta} \frac{h(x)-h(b)}{{\lambda}(D)} \right)
= \sum_{y \leqslant X/(W{\kappa})}
e\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta} f_d(y)
\right),
\end{equation*} where cd is the leading coefficient of h and ![]() $f_d(y) \in \mathbb{Z}[y]$ is monic of degree d.
$f_d(y) \in \mathbb{Z}[y]$ is monic of degree d.
Suppose ![]() $X^{1/2} \leqslant P \leqslant X$. The exponential sum
$X^{1/2} \leqslant P \leqslant X$. The exponential sum
 \begin{equation*}
g_1({\alpha}; P) :=
\sum_{y \leqslant P/(W{\kappa})}
e({\alpha} f_d(y))
\end{equation*}
\begin{equation*}
g_1({\alpha}; P) :=
\sum_{y \leqslant P/(W{\kappa})}
e({\alpha} f_d(y))
\end{equation*} can be treated using Roger Baker’s estimates [Reference Baker1]. We apply the formulation [Reference Chow3, lemma 2.3], noting from its proof that the quantity ![]() ${\sigma}(d)$ therein can be replaced by
${\sigma}(d)$ therein can be replaced by ![]() $2^{1-d}$. This delivers the following conclusion.
$2^{1-d}$. This delivers the following conclusion.
Lemma 6.4. If  $|g_1({\alpha}; P)| \gt (P/(W{\kappa}))^{1 - 2^{1-d} + \varepsilon}$, then there exist coprime
$|g_1({\alpha}; P)| \gt (P/(W{\kappa}))^{1 - 2^{1-d} + \varepsilon}$, then there exist coprime ![]() $r \in \mathbb{N}$ and
$r \in \mathbb{N}$ and ![]() $b \in \mathbb{Z}$ such that
$b \in \mathbb{Z}$ such that
 \begin{equation*}
g_1({\alpha}; P) \ll_{d,\varepsilon} r^{\varepsilon-1/d}
P(W{\kappa})^{-1}
(1 + (P/(W{\kappa}))^d
|{\alpha} - b/r|)^{-1/d}.
\end{equation*}
\begin{equation*}
g_1({\alpha}; P) \ll_{d,\varepsilon} r^{\varepsilon-1/d}
P(W{\kappa})^{-1}
(1 + (P/(W{\kappa}))^d
|{\alpha} - b/r|)^{-1/d}.
\end{equation*}Lemma 6.5. Let
 \begin{equation*}
\mathfrak n = \{{\theta} \in \mathbb{T}:
|\hat \mu({\theta})|
\leqslant X^{d-2^{-d}} \}.
\end{equation*}
\begin{equation*}
\mathfrak n = \{{\theta} \in \mathbb{T}:
|\hat \mu({\theta})|
\leqslant X^{d-2^{-d}} \}.
\end{equation*} If ![]() ${\theta} \in \mathbb{T} \setminus \mathfrak n$, then there exist coprime
${\theta} \in \mathbb{T} \setminus \mathfrak n$, then there exist coprime ![]() $q \in \mathbb{N}$ and
$q \in \mathbb{N}$ and ![]() $a \in \mathbb{Z}$ such that
$a \in \mathbb{Z}$ such that
 \begin{equation*}
\hat \mu({\theta}) \ll_{d,\varepsilon}
N (\log X) q^{\varepsilon-1/d}
(1 + N|{\theta} - a/q|)^{-1/d}.
\end{equation*}
\begin{equation*}
\hat \mu({\theta}) \ll_{d,\varepsilon}
N (\log X) q^{\varepsilon-1/d}
(1 + N|{\theta} - a/q|)^{-1/d}.
\end{equation*}Proof. Let ![]() $P \in [X^{1/2}, X]$ maximize
$P \in [X^{1/2}, X]$ maximize
 \begin{equation*}
\left|g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)\right|.
\end{equation*}
\begin{equation*}
\left|g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)\right|.
\end{equation*}By (6.1),
 \begin{equation*}
\left|g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)\right| \gt (P/(W{\kappa}))^{1 - 2^{1-d} + \varepsilon}.
\end{equation*}
\begin{equation*}
\left|g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)\right| \gt (P/(W{\kappa}))^{1 - 2^{1-d} + \varepsilon}.
\end{equation*} By lemma 6.4, there exist coprime ![]() $r \in \mathbb{N}$ and
$r \in \mathbb{N}$ and ![]() $b \in \mathbb{Z}$ such that
$b \in \mathbb{Z}$ such that
 \begin{align*}
g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)
&\ll r^{\varepsilon-1/d}
P(W{\kappa})^{-1}
\left(1 + (P/(W{\kappa}))^d
\left|\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta} - b/r \right| \right)^{-1/d} \\
&\ll r^{\varepsilon-1/d}
X(W{\kappa})^{-1}
\left(1 + (X/(W{\kappa}))^d
\left|\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta} - b/r \right| \right)^{-1/d}.
\end{align*}
\begin{align*}
g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)
&\ll r^{\varepsilon-1/d}
P(W{\kappa})^{-1}
\left(1 + (P/(W{\kappa}))^d
\left|\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta} - b/r \right| \right)^{-1/d} \\
&\ll r^{\varepsilon-1/d}
X(W{\kappa})^{-1}
\left(1 + (X/(W{\kappa}))^d
\left|\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta} - b/r \right| \right)^{-1/d}.
\end{align*}With
 \begin{equation*}
a = \frac{b}
{(b, c_d (W{\kappa})^d/{\lambda}(D))},
\qquad
q = \frac{rc_d (W{\kappa})^d/{\lambda}(D)}
{(b, c_d (W{\kappa})^d/{\lambda}(D))},
\end{equation*}
\begin{equation*}
a = \frac{b}
{(b, c_d (W{\kappa})^d/{\lambda}(D))},
\qquad
q = \frac{rc_d (W{\kappa})^d/{\lambda}(D)}
{(b, c_d (W{\kappa})^d/{\lambda}(D))},
\end{equation*}we now have
 \begin{align*}
g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)
&\ll r^{\varepsilon-1/d}
\frac{X}{W{\kappa}}
\left(1 + \frac{X^d}{{\lambda}(D)} |{\theta}-a/q| \right)^{-1/d} \\
&\ll q^{\varepsilon-1/d}
\frac{X\log X}{W{\kappa}}
\left(1 + \frac{X^d}{{\lambda}(D)} |{\theta}-a/q| \right)^{-1/d},
\end{align*}
\begin{align*}
g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right)
&\ll r^{\varepsilon-1/d}
\frac{X}{W{\kappa}}
\left(1 + \frac{X^d}{{\lambda}(D)} |{\theta}-a/q| \right)^{-1/d} \\
&\ll q^{\varepsilon-1/d}
\frac{X\log X}{W{\kappa}}
\left(1 + \frac{X^d}{{\lambda}(D)} |{\theta}-a/q| \right)^{-1/d},
\end{align*}since X is large in terms of w. Finally, recall that
 \begin{equation*}
N \asymp \frac{X^d}{{\lambda}(D)}
= \frac{X^d}{W{\kappa}(h'(b),W)}
\end{equation*}
\begin{equation*}
N \asymp \frac{X^d}{{\lambda}(D)}
= \frac{X^d}{W{\kappa}(h'(b),W)}
\end{equation*}and
 \begin{equation*}
X^{d-2^{-d}} \lt |\hat{\mu}({\theta})| \ll
X^{d-1} + \frac{X^{d-1}}
{(h'(b),W)} g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right).
\end{equation*}
\begin{equation*}
X^{d-2^{-d}} \lt |\hat{\mu}({\theta})| \ll
X^{d-1} + \frac{X^{d-1}}
{(h'(b),W)} g_1\left(
\frac{c_d (W{\kappa})^d}{{\lambda}(D)} {\theta}; P \right).
\end{equation*}By passing to a slightly higher moment, we are now able to obtain a log-slack analogue of lemma 6.3.
Lemma 6.6. (Log-slack estimate)
Let ![]() $v \gt 2T$ be real, and let
$v \gt 2T$ be real, and let ![]() $\psi: \mathbb{Z} \to \mathbb{C}$ with
$\psi: \mathbb{Z} \to \mathbb{C}$ with ![]() $|\psi| \leqslant \mu$. Then,
$|\psi| \leqslant \mu$. Then,
 \begin{equation*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^v {\,{\rm d}} {\alpha} \ll_{h,v} N^{v-1} (\log X)^v.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^v {\,{\rm d}} {\alpha} \ll_{h,v} N^{v-1} (\log X)^v.
\end{equation*}Proof. Inserting lemmas 6.3 and 6.5 into lemma 2.3 gives
 \begin{equation*}
\int_{\mathbb{T}}
(|\hat \psi({\alpha})|
/\log X)^v
{\,{\rm d}} {\alpha} \ll N^{v-1}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}}
(|\hat \psi({\alpha})|
/\log X)^v
{\,{\rm d}} {\alpha} \ll N^{v-1}.
\end{equation*}Proof of proposition 6.1
Let ![]() $v \in (2T, E)$. Applying lemma 6.6 to
$v \in (2T, E)$. Applying lemma 6.6 to ![]() $\psi = (\log X)^{-1} \phi$ gives the log-slack restriction estimate
$\psi = (\log X)^{-1} \phi$ gives the log-slack restriction estimate
 \begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^v {\,{\rm d}} {\alpha} \ll_{h,v}
N^{v-1} (\log X)^{2v}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^v {\,{\rm d}} {\alpha} \ll_{h,v}
N^{v-1} (\log X)^{2v}.
\end{equation*}We can choose σd to be large in terms of E and v. Thus, in view of corollaries 5.3 and 5.6, the desired result follows from lemma 2.3.
6.2. Restriction II
Define the auxiliary weight function ![]() $\nu_D: \mathbb{Z} \to [0,\infty)$ by
$\nu_D: \mathbb{Z} \to [0,\infty)$ by
 \begin{align*}
\nu_D(n) &=
\frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})
\\ h(p) = n {\lambda}(D)}}
h'(p) \log p \\
&=
\frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{z \leqslant Z \\
(Dz + r_D)\in\mathcal P_X
\\ h_D(z)=n}}
h'(Dz + r_D) \log(Dz + r_D) .
\end{align*}
\begin{align*}
\nu_D(n) &=
\frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})
\\ h(p) = n {\lambda}(D)}}
h'(p) \log p \\
&=
\frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{z \leqslant Z \\
(Dz + r_D)\in\mathcal P_X
\\ h_D(z)=n}}
h'(Dz + r_D) \log(Dz + r_D) .
\end{align*} Observe that νD is supported on ![]() $h_D([Z])\subseteq [N]$. By the Siegel–Walfisz theorem, we have
$h_D([Z])\subseteq [N]$. By the Siegel–Walfisz theorem, we have
 \begin{align*}
\| \nu_D \|_1
&= \frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})}}
h'(p) \log p \\
&\leqslant \frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})}} h'(X) \log X
\ll N.
\end{align*}
\begin{align*}
\| \nu_D \|_1
&= \frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})}}
h'(p) \log p \\
&\leqslant \frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})}} h'(X) \log X
\ll N.
\end{align*}One can be more precise using partial summation, but we do not need to.
In this subsection, we establish the following restriction estimate for νD.
Proposition 6.7. Let ![]() $E \gt 2T$ be real, and let
$E \gt 2T$ be real, and let ![]() $\phi: \mathbb{Z} \to \mathbb{C}$ with
$\phi: \mathbb{Z} \to \mathbb{C}$ with ![]() $|\phi| \leqslant \nu_D$. Then,
$|\phi| \leqslant \nu_D$. Then,
 \begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^E {\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^E {\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*}Our approach is similar to that of proposition 6.1, so we will not repeat all of the details. We introduce the auxiliary function
 \begin{equation*}
\mu_D: \mathbb{Z} \to [0,\infty),
\qquad
\mu_D(n) =
\frac{ND}{X}
\sum_{\substack{z \leqslant Z
\\ h_D(z) = n}} 1,
\end{equation*}
\begin{equation*}
\mu_D: \mathbb{Z} \to [0,\infty),
\qquad
\mu_D(n) =
\frac{ND}{X}
\sum_{\substack{z \leqslant Z
\\ h_D(z) = n}} 1,
\end{equation*} noting that ![]() $\nu_D \ll (\log X) \mu_D$ pointwise. As a special case of [Reference Chapman and Chow2, lemma 6.3], we have the following sharp restriction estimate for µD.
$\nu_D \ll (\log X) \mu_D$ pointwise. As a special case of [Reference Chapman and Chow2, lemma 6.3], we have the following sharp restriction estimate for µD.
Lemma 6.8. Let ![]() $E \gt 2T$, and let
$E \gt 2T$, and let ![]() $\psi: \mathbb{Z} \to \mathbb{C}$ with
$\psi: \mathbb{Z} \to \mathbb{C}$ with ![]() $|\psi| \leqslant \mu_D$. Then,
$|\psi| \leqslant \mu_D$. Then,
 \begin{equation*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^E
{\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{T}} |\hat \psi({\alpha})|^E
{\,{\rm d}} {\alpha} \ll_{h,E} N^{E-1}.
\end{equation*} The upshot is that if ![]() $v \gt 2T$ and
$v \gt 2T$ and ![]() $|\phi| \leqslant \nu_D$, then
$|\phi| \leqslant \nu_D$, then
 \begin{equation}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^v
{\,{\rm d}} {\alpha}
\ll_v N^{v-1} (\log X)^v.
\end{equation}
\begin{equation}
\int_{\mathbb{T}} |\hat \phi({\alpha})|^v
{\,{\rm d}} {\alpha}
\ll_v N^{v-1} (\log X)^v.
\end{equation}To apply the general epsilon-removal lemma, we require major and minor arc bounds for
 \begin{equation*}
\hat \nu_D({\alpha})
= \frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})}}
h'(p) \log p \cdot
e({\alpha} h(p) / {\lambda}(D)).
\end{equation*}
\begin{equation*}
\hat \nu_D({\alpha})
= \frac{\varphi(D)}{{\lambda}(D)}
\sum_{\substack{p \leqslant X \\
p \equiv r_D \;(\operatorname{mod}{D})}}
h'(p) \log p \cdot
e({\alpha} h(p) / {\lambda}(D)).
\end{equation*}On the minor arcs, we infer the following analogue of corollary 5.3, by essentially the same argument:
On the major arcs, we have (5.2), for some ![]() $q,a \in \mathbb{Z}$. Define
$q,a \in \mathbb{Z}$. Define
 \begin{equation*}
S_D(q,a) = \sum_{\substack{t \;(\operatorname{mod}{Dq}) \\ (t,q) = 1 \\
t \equiv r_D \;(\operatorname{mod}{D})}}
e_q(ah(t)/{\lambda}(D)).
\end{equation*}
\begin{equation*}
S_D(q,a) = \sum_{\substack{t \;(\operatorname{mod}{Dq}) \\ (t,q) = 1 \\
t \equiv r_D \;(\operatorname{mod}{D})}}
e_q(ah(t)/{\lambda}(D)).
\end{equation*}We infer the following analogue of corollary 5.4 by essentially the same proof.
Lemma 6.9. Let c be a small, positive constant, small in terms of Cd. Suppose ![]() $({\alpha}, q, a) \in
\mathbb{R} \times \mathbb{N} \times \mathbb{Z}$ with (5.2), and put
$({\alpha}, q, a) \in
\mathbb{R} \times \mathbb{N} \times \mathbb{Z}$ with (5.2), and put ![]() ${\beta} = {\alpha} - a/q$. Then,
${\beta} = {\alpha} - a/q$. Then,
 \begin{equation*}
\hat \nu_D({\alpha}) =
\frac{\varphi(D)}
{\varphi(Dq)}
S_D(q,a) I({\beta})
+ O(Ne^{-c \sqrt{\log X}}).
\end{equation*}
\begin{equation*}
\hat \nu_D({\alpha}) =
\frac{\varphi(D)}
{\varphi(Dq)}
S_D(q,a) I({\beta})
+ O(Ne^{-c \sqrt{\log X}}).
\end{equation*}It follows from lemma 2.2 that
 \begin{equation*}
S_D(q,a) \ll_{h,\varepsilon} q^{\varepsilon-1/d}
\varphi(q).
\end{equation*}
\begin{equation*}
S_D(q,a) \ll_{h,\varepsilon} q^{\varepsilon-1/d}
\varphi(q).
\end{equation*}Thus, by incorporating (5.6), we arrive at the following variant of corollary 5.6:
 \begin{equation}
\hat \nu_D({\alpha})
\ll_{h,\varepsilon} q^{\varepsilon - 1/d}
\min \{N, \| {\alpha} - a/q \|^{-1} \}
+ O(Ne^{-c \sqrt{\log X}}).
\end{equation}
\begin{equation}
\hat \nu_D({\alpha})
\ll_{h,\varepsilon} q^{\varepsilon - 1/d}
\min \{N, \| {\alpha} - a/q \|^{-1} \}
+ O(Ne^{-c \sqrt{\log X}}).
\end{equation}Equipped with the bounds (6.1), (6.2), and (6.3), proposition 6.7 now follows from the general epsilon-removal lemma (lemma 2.3).
7. The transference principle
In this section, we are finally ready to use transference to deduce theorem 2.6 from theorem 2.8. We start with some notation and a preparatory lemma.
For finitely-supported ![]() $f_1, \ldots, f_s, g_1, \ldots, g_t: \mathbb{Z} \to \mathbb{R}$, define
$f_1, \ldots, f_s, g_1, \ldots, g_t: \mathbb{Z} \to \mathbb{R}$, define
 \begin{equation*}
\Phi(f_1,\ldots,f_s;
g_1, \ldots, g_t) =
\sum_{L_1({\mathbf{n}}) = L_2(\mathbf{m})}
f_1(n_1) \cdots f_s(n_s)
g_1(m_1) \cdots g_t(m_t).
\end{equation*}
\begin{equation*}
\Phi(f_1,\ldots,f_s;
g_1, \ldots, g_t) =
\sum_{L_1({\mathbf{n}}) = L_2(\mathbf{m})}
f_1(n_1) \cdots f_s(n_s)
g_1(m_1) \cdots g_t(m_t).
\end{equation*}We frequently make use of the abbreviations
Given finite sets of integers A and B, we also write ![]() $\Phi(A;g) = \Phi(1_A; g)$, and similarly for the expressions
$\Phi(A;g) = \Phi(1_A; g)$, and similarly for the expressions ![]() $\Phi(f;B)$ and
$\Phi(f;B)$ and ![]() $\Phi(A;B)$.
$\Phi(A;B)$.
Lemma 7.1. (Fourier control)
Let ![]() $f_1, \ldots, f_s, g: \mathbb{Z} \to \mathbb{R}$ be finitely supported. If
$f_1, \ldots, f_s, g: \mathbb{Z} \to \mathbb{R}$ be finitely supported. If
then
 \begin{equation*}
\Phi(f_1,\ldots,f_s; g)
\ll N^{s+t-1} \prod_{j \leqslant s}
(\| \hat f_j \|_\infty
/ N)^{1/(2s+2t)}.
\end{equation*}
\begin{equation*}
\Phi(f_1,\ldots,f_s; g)
\ll N^{s+t-1} \prod_{j \leqslant s}
(\| \hat f_j \|_\infty
/ N)^{1/(2s+2t)}.
\end{equation*}Proof. Following the proof of [Reference Chapman and Chow2, lemma 7.1] yields
 \begin{align*}
|\Phi(f_1,\ldots,f_s;g)|
&\leqslant
\left(
\int_{\mathbb{T}} |\hat g({\alpha})|^{s+t} {\,{\rm d}} {\alpha}
\right)^{t/(s+t)}\notag\\ & \quad \cdot
\prod_{j \leqslant s}
\left( \| \hat f_j \|_\infty^{1/2}
\int_{\mathbb{T}} |\hat f_j({\alpha})|^{s+t-1/2}
{\,{\rm d}} {\alpha}
\right)^{1/(s+t)}.
\end{align*}
\begin{align*}
|\Phi(f_1,\ldots,f_s;g)|
&\leqslant
\left(
\int_{\mathbb{T}} |\hat g({\alpha})|^{s+t} {\,{\rm d}} {\alpha}
\right)^{t/(s+t)}\notag\\ & \quad \cdot
\prod_{j \leqslant s}
\left( \| \hat f_j \|_\infty^{1/2}
\int_{\mathbb{T}} |\hat f_j({\alpha})|^{s+t-1/2}
{\,{\rm d}} {\alpha}
\right)^{1/(s+t)}.
\end{align*}Propositions 6.2 and 6.7 now give
 \begin{align*}
\Phi(f_1,\ldots,f_s;g) &\ll
N^{(s+t-1)t/(s+t)}
\prod_{j \leqslant s}
\left(
\| \hat f_j \|_\infty^{1/(2s+2t)}
N^{(s+t-3/2)/(s+t)} \right) \\
&= N^{s+t-1}
\prod_{j \leqslant s} (\| \hat f_j \|_\infty / N)^{1/(2s+2t)}.
\end{align*}
\begin{align*}
\Phi(f_1,\ldots,f_s;g) &\ll
N^{(s+t-1)t/(s+t)}
\prod_{j \leqslant s}
\left(
\| \hat f_j \|_\infty^{1/(2s+2t)}
N^{(s+t-3/2)/(s+t)} \right) \\
&= N^{s+t-1}
\prod_{j \leqslant s} (\| \hat f_j \|_\infty / N)^{1/(2s+2t)}.
\end{align*}Proof of theorem 2.6 given theorem 2.8
Fix ![]() ${\delta}, h, r, L_1,$ and L 2. The implied constants are henceforth allowed to depend on all of these parameters. Let
${\delta}, h, r, L_1,$ and L 2. The implied constants are henceforth allowed to depend on all of these parameters. Let ![]() $\tilde {\delta}$ be small in terms of the fixed parameters, and let
$\tilde {\delta}$ be small in terms of the fixed parameters, and let ![]() $w \in \mathbb{N}$ be large in terms of them. We insist that
$w \in \mathbb{N}$ be large in terms of them. We insist that ![]() $\tilde {\delta}$ is an integer power of 2, and that
$\tilde {\delta}$ is an integer power of 2, and that ![]() $\tilde {\delta} \gg 1$, so that dependence on
$\tilde {\delta} \gg 1$, so that dependence on ![]() $\tilde {\delta}$ is subsumed by dependence on the fixed parameters.
$\tilde {\delta}$ is subsumed by dependence on the fixed parameters.
Given sufficiently large ![]() $X\in\mathbb{N}$, we define
$X\in\mathbb{N}$, we define ![]() $D,N,W,Z$ as in §3. For the purposes of proving theorem 2.6, we may assume that
$D,N,W,Z$ as in §3. For the purposes of proving theorem 2.6, we may assume that ![]() $Z\in\mathbb{N}$. Indeed, assuming X is sufficiently large relative to D, any
$Z\in\mathbb{N}$. Indeed, assuming X is sufficiently large relative to D, any ![]() $A\subseteq\mathcal P_X$ with
$A\subseteq\mathcal P_X$ with ![]() $|A|\geqslant\delta |\mathcal P_X|$ must satisfy
$|A|\geqslant\delta |\mathcal P_X|$ must satisfy ![]() $|A\cap[X-D]| \gt (\delta/2)|\mathcal P_X|$. Thus, by replacing
$|A\cap[X-D]| \gt (\delta/2)|\mathcal P_X|$. Thus, by replacing ![]() $(\delta,A,X)$ with
$(\delta,A,X)$ with ![]() $(\delta/2,A\cap[X-a],X-a)$ for some
$(\delta/2,A\cap[X-a],X-a)$ for some ![]() $a\in[D]$ such that
$a\in[D]$ such that ![]() $D\mid(X-a-r_D)$, we can assume that
$D\mid(X-a-r_D)$, we can assume that ![]() $D\mid(X-r_D)$, whence
$D\mid(X-r_D)$, whence ![]() $Z\in\mathbb{N}$.
$Z\in\mathbb{N}$.
Set
By theorem 2.8, there exists ![]() $k \in [r]$ such that every
$k \in [r]$ such that every ![]() $\tilde{\mathcal{A}} \subseteq [N]$ with
$\tilde{\mathcal{A}} \subseteq [N]$ with ![]() $|\tilde{\mathcal{A}}| \geqslant \tilde {\delta} N$ satisfies
$|\tilde{\mathcal{A}}| \geqslant \tilde {\delta} N$ satisfies
 \begin{equation*}
\# \{({\mathbf{n}}, \mathbf{z}) \in \tilde{\mathcal{A}}^s \times \tilde{\mathcal{C}}_k^t:
L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \}
\gg N^{s-1} \left(
\frac{DZ}{\varphi(D)\log Z}
\right)^t.
\end{equation*}
\begin{equation*}
\# \{({\mathbf{n}}, \mathbf{z}) \in \tilde{\mathcal{A}}^s \times \tilde{\mathcal{C}}_k^t:
L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \}
\gg N^{s-1} \left(
\frac{DZ}{\varphi(D)\log Z}
\right)^t.
\end{equation*} By a simple counting argument, the number of solutions counted here for any given value of zt is ![]() $O(|\tilde C_k| N^{s-1}
(Z/\log Z)^{t-1})$, whence
$O(|\tilde C_k| N^{s-1}
(Z/\log Z)^{t-1})$, whence ![]() $|\tilde{\mathcal{C}}_k| \gg Z/\log Z$. Thus,
$|\tilde{\mathcal{C}}_k| \gg Z/\log Z$. Thus,
 \begin{equation*}
|\mathcal C_k| \geqslant |\tilde{\mathcal{C}}_k|
\gg \frac{Z}{\log Z} \gg_w
\frac{X}{\log X}.
\end{equation*}
\begin{equation*}
|\mathcal C_k| \geqslant |\tilde{\mathcal{C}}_k|
\gg \frac{Z}{\log Z} \gg_w
\frac{X}{\log X}.
\end{equation*} Define ![]() $\mathcal A$ by (3.3), and define
$\mathcal A$ by (3.3), and define
 \begin{equation*}
f = \nu 1_\mathcal A,
\qquad
g_i(n) =
\frac{N \varphi(D) \log Z}{DZ}
\sum_{\substack{
z \in \tilde C_i \\ h_D(z) = n}}1
\quad (1 \leqslant i \leqslant r).
\end{equation*}
\begin{equation*}
f = \nu 1_\mathcal A,
\qquad
g_i(n) =
\frac{N \varphi(D) \log Z}{DZ}
\sum_{\substack{
z \in \tilde C_i \\ h_D(z) = n}}1
\quad (1 \leqslant i \leqslant r).
\end{equation*}By lemma 5.1 and the dense model lemma [Reference Prendiville16, theorem 5.1], there exists a function f 0 such that
 \begin{equation*}
0 \leqslant f_0 \leqslant 1_{[N]},
\qquad
\| \hat f - \hat f_0 \|_\infty
\ll (\log w)^{-3/2} N.
\end{equation*}
\begin{equation*}
0 \leqslant f_0 \leqslant 1_{[N]},
\qquad
\| \hat f - \hat f_0 \|_\infty
\ll (\log w)^{-3/2} N.
\end{equation*} For ![]() $\ell \in [s]$, we write
$\ell \in [s]$, we write  $\mathbf{u}^{(\ell)} = (u_1^{(\ell)},
\ldots, u_s^{(\ell)})$, where
$\mathbf{u}^{(\ell)} = (u_1^{(\ell)},
\ldots, u_s^{(\ell)})$, where
 \begin{equation*}
u_j^{(\ell)} =
\begin{cases}
f_0, &\text{if } j \lt \ell \\
f-f_0, &\text{if } j = \ell \\
f, &\text{if } j \gt \ell.
\end{cases}
\end{equation*}
\begin{equation*}
u_j^{(\ell)} =
\begin{cases}
f_0, &\text{if } j \lt \ell \\
f-f_0, &\text{if } j = \ell \\
f, &\text{if } j \gt \ell.
\end{cases}
\end{equation*}The telescoping identity and lemma 7.1 now give
 \begin{equation}
\Phi(f; g_i) - \Phi(f_0; g_i)
= \sum_{\ell \leqslant s}
\Phi(\mathbf{u}^{(\ell)}; g_i)
\ll (\log w)^{-3/(4s + 4t)}
N^{s+t-1} \quad (1 \leqslant i \leqslant r).
\end{equation}
\begin{equation}
\Phi(f; g_i) - \Phi(f_0; g_i)
= \sum_{\ell \leqslant s}
\Phi(\mathbf{u}^{(\ell)}; g_i)
\ll (\log w)^{-3/(4s + 4t)}
N^{s+t-1} \quad (1 \leqslant i \leqslant r).
\end{equation}By lemma 3.1, we have
 \begin{equation*}
\sum_{n \in \mathbb{Z}} f(n) \gg N.
\end{equation*}
\begin{equation*}
\sum_{n \in \mathbb{Z}} f(n) \gg N.
\end{equation*} Since  $\hat f(0) - \hat f_0(0) \ll (\log w)^{-3/2}$, and w is large, we also have
$\hat f(0) - \hat f_0(0) \ll (\log w)^{-3/2}$, and w is large, we also have
 \begin{equation*}
\sum_{n \in \mathbb{Z}} f_0(n) \gg N.
\end{equation*}
\begin{equation*}
\sum_{n \in \mathbb{Z}} f_0(n) \gg N.
\end{equation*}Let c be a small, positive constant that depends only on the fixed parameters. Setting
we observe that
 \begin{equation*}
N \ll \sum_{n\in\tilde{\mathcal{A}}}f_0(n) + \sum_{n\in[N]\setminus\tilde{\mathcal{A}}}f_0(n) \leqslant |\tilde{\mathcal A}| + cN.
\end{equation*}
\begin{equation*}
N \ll \sum_{n\in\tilde{\mathcal{A}}}f_0(n) + \sum_{n\in[N]\setminus\tilde{\mathcal{A}}}f_0(n) \leqslant |\tilde{\mathcal A}| + cN.
\end{equation*} Taking c sufficiently small, therefore, allows us to extract the lower bound ![]() $|\tilde{\mathcal{A}}| \geqslant \tilde {\delta} N$. Now theorem 2.8 gives
$|\tilde{\mathcal{A}}| \geqslant \tilde {\delta} N$. Now theorem 2.8 gives ![]() $
\Phi(\tilde{\mathcal{A}}; g_k) \gg
N^{s+t-1}.
$ Since
$
\Phi(\tilde{\mathcal{A}}; g_k) \gg
N^{s+t-1}.
$ Since ![]() $0\leqslant c1_{\tilde{A}}\leqslant f_0$, it follows that
$0\leqslant c1_{\tilde{A}}\leqslant f_0$, it follows that ![]() $\Phi(f_0; g_k) \gg N^{s+t-1}$. Taking w sufficiently large, we infer from (7.1) that
$\Phi(f_0; g_k) \gg N^{s+t-1}$. Taking w sufficiently large, we infer from (7.1) that
Finally, since ![]() $N\leqslant h(X)\asymp X^d$, we conclude that
$N\leqslant h(X)\asymp X^d$, we conclude that
 \begin{align*}
&\# \{(\mathbf{x}, \mathbf{y}) \in A^s \times \mathcal C_k^t: L_1(h(\mathbf{x})) = L_2(h(\mathbf{y})) \}
\\
&\geqslant \| f \|_\infty^{-s}
\| g_k \|_\infty^{-t} \Phi(f; g_k)
\gg_w
\left(
\frac{N \log X}{X}
\right)^{-s}
\left( \frac{N \log X}{X}
\right)^{-t}
N^{s+t-1} \\
&\gg_w
\frac{X^{s+t-d}}{(\log X)^{s+t}}.
\end{align*}
\begin{align*}
&\# \{(\mathbf{x}, \mathbf{y}) \in A^s \times \mathcal C_k^t: L_1(h(\mathbf{x})) = L_2(h(\mathbf{y})) \}
\\
&\geqslant \| f \|_\infty^{-s}
\| g_k \|_\infty^{-t} \Phi(f; g_k)
\gg_w
\left(
\frac{N \log X}{X}
\right)^{-s}
\left( \frac{N \log X}{X}
\right)^{-t}
N^{s+t-1} \\
&\gg_w
\frac{X^{s+t-d}}{(\log X)^{s+t}}.
\end{align*} By specifying that ![]() $w=O_{\delta,h,r,L_1,L_2}(1)$, this completes the proof.
$w=O_{\delta,h,r,L_1,L_2}(1)$, this completes the proof.
8. Arithmetic regularity
Our only remaining task is to prove theorem 2.8. We are, therefore, interested in counting solutions to the linearized equation (2.7). We seek a colour class ![]() $\mathcal C_k$ such that there are many solutions
$\mathcal C_k$ such that there are many solutions ![]() $({\mathbf{n}},\mathbf{z})$ to (2.7) with
$({\mathbf{n}},\mathbf{z})$ to (2.7) with ![]() ${\mathbf{n}}\in\mathcal C_k^t$ and
${\mathbf{n}}\in\mathcal C_k^t$ and ![]() $\mathbf{z}\in\mathcal A^s$ for some arbitrary dense set
$\mathbf{z}\in\mathcal A^s$ for some arbitrary dense set ![]() $\mathcal A\subseteq [N]$.
$\mathcal A\subseteq [N]$.
Following [Reference Prendiville17] and [Reference Chapman and Chow2], we begin by weakening the statement of theorem 2.8. Rather than assert the existence of a colour class ![]() $\mathcal C_k$ which gives many solutions with respect to all dense sets
$\mathcal C_k$ which gives many solutions with respect to all dense sets ![]() $\mathcal A$, we instead consider a finite collection of dense sets
$\mathcal A$, we instead consider a finite collection of dense sets ![]() $\mathcal A_1,\ldots,\mathcal A_r\subseteq[N]$ and seek a colour class
$\mathcal A_1,\ldots,\mathcal A_r\subseteq[N]$ and seek a colour class ![]() $\mathcal C_k$ such that, for all
$\mathcal C_k$ such that, for all ![]() $i\in[r]$, there are many solutions to (2.7) with
$i\in[r]$, there are many solutions to (2.7) with ![]() $({\mathbf{n}},\mathbf{z})\in\mathcal A_i^s\times\mathcal C_k^t$. This leads to the following version of theorem 2.8.
$({\mathbf{n}},\mathbf{z})\in\mathcal A_i^s\times\mathcal C_k^t$. This leads to the following version of theorem 2.8.
Theorem 8.1 Let r and ![]() $d\geqslant 2$ be positive integers, and let
$d\geqslant 2$ be positive integers, and let ![]() $0 \lt \delta\leqslant 1$. Let h be an integer polynomial of degree d, which is intersective of the second kind. Let
$0 \lt \delta\leqslant 1$. Let h be an integer polynomial of degree d, which is intersective of the second kind. Let ![]() $s \geqslant 1$ and
$s \geqslant 1$ and ![]() $t \geqslant 0$ be integers such that
$t \geqslant 0$ be integers such that ![]() $s + t \geqslant s_0(d)$. Let
$s + t \geqslant s_0(d)$. Let
be non-degenerate linear forms such that ![]() $L_1(1,\ldots,1) = 0$ and
$L_1(1,\ldots,1) = 0$ and ![]() $\gcd(L_1)=1$. Then, there exists
$\gcd(L_1)=1$. Then, there exists ![]() $\eta=\eta(d,\delta,L_1,L_2)\in(0,1)$ such that the following is true. Let
$\eta=\eta(d,\delta,L_1,L_2)\in(0,1)$ such that the following is true. Let ![]() $D, Z \in \mathbb{N}$ satisfy
$D, Z \in \mathbb{N}$ satisfy ![]() $Z \geqslant Z_0(D, h, r, {\delta}, L_1, L_2)$, and set
$Z \geqslant Z_0(D, h, r, {\delta}, L_1, L_2)$, and set ![]() $N:=h_D(Z)$. Suppose
$N:=h_D(Z)$. Suppose ![]() $\mathcal A_1,\ldots,\mathcal A_r\subseteq[N]$ satisfy
$\mathcal A_1,\ldots,\mathcal A_r\subseteq[N]$ satisfy ![]() $|\mathcal A_i|\geqslant\delta N$ for all
$|\mathcal A_i|\geqslant\delta N$ for all ![]() $i\in[r]$. If
$i\in[r]$. If
then there exists ![]() $k \in [r]$ such that
$k \in [r]$ such that
 \begin{equation*}
\# \{({\mathbf{n}},\mathbf{z}) \in \mathcal A_i^s \times \mathcal C_k^t: L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \} \gg
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \qquad(1\leqslant i\leqslant r).
\end{equation*}
\begin{equation*}
\# \{({\mathbf{n}},\mathbf{z}) \in \mathcal A_i^s \times \mathcal C_k^t: L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \} \gg
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \qquad(1\leqslant i\leqslant r).
\end{equation*} The implied constant may depend on ![]() $h, L_1, L_2, r, \delta$.
$h, L_1, L_2, r, \delta$.
Proof of theorem 2.8 given theorem 8.1
In view of proposition 2.10, it is enough to prove theorem 2.8 under the assumption that ![]() $\gcd(L_1)=1$. We claim that theorem 2.8 holds with the same quantities
$\gcd(L_1)=1$. We claim that theorem 2.8 holds with the same quantities ![]() $Z_0(D,h,r,\delta,L_1,L_2)$,
$Z_0(D,h,r,\delta,L_1,L_2)$, ![]() $\eta(d,\delta,L_1,L_2)$, and the same implicit constant
$\eta(d,\delta,L_1,L_2)$, and the same implicit constant ![]() $C=C(h,L_1,L_2,r,\delta)$ appearing in the final bound. Suppose for a contradiction that this is false. For each
$C=C(h,L_1,L_2,r,\delta)$ appearing in the final bound. Suppose for a contradiction that this is false. For each ![]() $k\in[r]$, we can then find
$k\in[r]$, we can then find ![]() $\mathcal A_k\subseteq[N]$ with
$\mathcal A_k\subseteq[N]$ with ![]() $|\mathcal A_k|\geqslant\delta N$ such that
$|\mathcal A_k|\geqslant\delta N$ such that
 \begin{equation*}
\# \{({\mathbf{n}},\mathbf{z}) \in \mathcal A_k^s \times \mathcal C_k^t: L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \} \lt CN^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t.
\end{equation*}
\begin{equation*}
\# \{({\mathbf{n}},\mathbf{z}) \in \mathcal A_k^s \times \mathcal C_k^t: L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z})) \} \lt CN^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t.
\end{equation*} Applying theorem 8.1 to the collection of dense sets ![]() $\mathcal A_1,\ldots,\mathcal A_r$ delivers a contradiction.
$\mathcal A_1,\ldots,\mathcal A_r$ delivers a contradiction.
By taking Z sufficiently large relative to η in theorem 8.1, we may assume that hD is positive and strictly increasing on the real interval ![]() $[\eta Z, Z]$. We can then define a function
$[\eta Z, Z]$. We can then define a function ![]() $\mathcal Q_{Z}=\mathcal Q_{Z;\eta,h_D}:\mathbb{Z}\to\mathbb{R}$ by
$\mathcal Q_{Z}=\mathcal Q_{Z;\eta,h_D}:\mathbb{Z}\to\mathbb{R}$ by
 \begin{equation*}
\mathcal Q_Z(t) :=
\begin{cases}
z, &\text{if }z\in[\eta Z, Z]\,\, \text{satisfies } t=h_D(z) \\
0, &\text{otherwise}.
\end{cases}
\end{equation*}
\begin{equation*}
\mathcal Q_Z(t) :=
\begin{cases}
z, &\text{if }z\in[\eta Z, Z]\,\, \text{satisfies } t=h_D(z) \\
0, &\text{otherwise}.
\end{cases}
\end{equation*} Notice that ![]() $\mathcal Q_Z$ is supported on
$\mathcal Q_Z$ is supported on ![]() $h_D([\eta Z, Z])\subseteq [N]$, and the restriction of
$h_D([\eta Z, Z])\subseteq [N]$, and the restriction of ![]() $\mathcal Q_Z$ to
$\mathcal Q_Z$ to ![]() $h_D([\eta Z, Z])$ defines a bijection from
$h_D([\eta Z, Z])$ defines a bijection from ![]() $h_D([\eta Z, Z])$ to
$h_D([\eta Z, Z])$ to ![]() $[\eta Z, Z]$. Hence, given functions
$[\eta Z, Z]$. Hence, given functions ![]() $f_1,\ldots,f_s:\mathbb{Z}\to\mathbb{R}$ supported on
$f_1,\ldots,f_s:\mathbb{Z}\to\mathbb{R}$ supported on ![]() $[N]$, and
$[N]$, and ![]() $g:\mathbb{Z}\to\mathbb{R}$ supported on
$g:\mathbb{Z}\to\mathbb{R}$ supported on ![]() $[\eta Z, Z]$, we have
$[\eta Z, Z]$, we have
 \begin{equation*}
\Phi(f_1,\ldots,f_s;
g\circ\mathcal Q_Z)
= \sum_{L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z}))}
f_1(n_1) \cdots f_s(n_s)
g(z_1) \cdots g(z_t).
\end{equation*}
\begin{equation*}
\Phi(f_1,\ldots,f_s;
g\circ\mathcal Q_Z)
= \sum_{L_1({\mathbf{n}}) = L_2(h_D(\mathbf{z}))}
f_1(n_1) \cdots f_s(n_s)
g(z_1) \cdots g(z_t).
\end{equation*}Lemma 8.2. (Arithmetic regularity lemma)
Let ![]() $r\in\mathbb{N}$, σ > 0, and let
$r\in\mathbb{N}$, σ > 0, and let ![]() $\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ be a monotone increasing function. Then, there exists a positive integer
$\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ be a monotone increasing function. Then, there exists a positive integer ![]() $K_{0}(r;{\sigma},\mathcal F)\in\mathbb{N}$ such that the following is true. Let
$K_{0}(r;{\sigma},\mathcal F)\in\mathbb{N}$ such that the following is true. Let ![]() $N\in\mathbb{N}$ and
$N\in\mathbb{N}$ and ![]() $f_{1},\ldots,f_r:[N]\to[0,1]$. Then, there is a positive integer
$f_{1},\ldots,f_r:[N]\to[0,1]$. Then, there is a positive integer ![]() $K\leqslant K_{0}(r;{\sigma},\mathcal F)$ and a phase
$K\leqslant K_{0}(r;{\sigma},\mathcal F)$ and a phase ![]() $\boldsymbol{\theta}\in\mathbb{T}^{K}$ such that, for every
$\boldsymbol{\theta}\in\mathbb{T}^{K}$ such that, for every ![]() $i\in[r]$, there is a decomposition
$i\in[r]$, there is a decomposition
 \begin{equation*}
f_{i}=f_{\mathrm{str}}^{(i)}+f_{\mathrm{sml}}^{(i)}+f_{\mathrm{unf}}^{(i)}
\end{equation*}
\begin{equation*}
f_{i}=f_{\mathrm{str}}^{(i)}+f_{\mathrm{sml}}^{(i)}+f_{\mathrm{unf}}^{(i)}
\end{equation*} of fi into functions  $f_{\mathrm{str}}^{(i)},f_{\mathrm{sml}}^{(i)},f_{\mathrm{unf}}^{(i)}:[N]\to[-1,1]$ with the following stipulations.
$f_{\mathrm{str}}^{(i)},f_{\mathrm{sml}}^{(i)},f_{\mathrm{unf}}^{(i)}:[N]\to[-1,1]$ with the following stipulations.
(I) The functions
 $f_{\mathrm{str}}^{(i)}$ and
$f_{\mathrm{str}}^{(i)}$ and  $f_{\mathrm{str}}^{(i)}+f_{\mathrm{sml}}^{(i)}$ take values in
$f_{\mathrm{str}}^{(i)}+f_{\mathrm{sml}}^{(i)}$ take values in  $[0,1]$.
$[0,1]$.(II) The function
 $f_{\mathrm{sml}}^{(i)}$ obeys the bound
$f_{\mathrm{sml}}^{(i)}$ obeys the bound  $\lVert f_{\mathrm{sml}}^{(i)}\rVert_{L^{2}(\mathbb{Z})}\leqslant{\sigma}\lVert 1_{[N]}\rVert_{L^{2}(\mathbb{Z})}$.
$\lVert f_{\mathrm{sml}}^{(i)}\rVert_{L^{2}(\mathbb{Z})}\leqslant{\sigma}\lVert 1_{[N]}\rVert_{L^{2}(\mathbb{Z})}$.(III) The function
 $f_{\mathrm{unf}}^{(i)}$ obeys the bound
$f_{\mathrm{unf}}^{(i)}$ obeys the bound  $\lVert \hat{f}_{\mathrm{unf}}^{(i)}\rVert_{\infty}\leqslant\lVert \hat{1}_{[N]}\rVert_{\infty}/\mathcal F(K)$.
$\lVert \hat{f}_{\mathrm{unf}}^{(i)}\rVert_{\infty}\leqslant\lVert \hat{1}_{[N]}\rVert_{\infty}/\mathcal F(K)$.(IV) The function
 $f_{\mathrm{str}}^{(i)}$ satisfies
$f_{\mathrm{str}}^{(i)}$ satisfies  $\sum_{m=1}^{N}(f_{i}-f_{\mathrm{str}}^{(i)})(m)=0$.
$\sum_{m=1}^{N}(f_{i}-f_{\mathrm{str}}^{(i)})(m)=0$.(V) There exists a K-Lipschitz function
 $F_{i}:\mathbb{T}^{K}\to[0,1]$ such that
$F_{i}:\mathbb{T}^{K}\to[0,1]$ such that  $F_{i}(x\boldsymbol{\theta} )=f_{\mathrm{str}}^{(i)}(x)$ for all
$F_{i}(x\boldsymbol{\theta} )=f_{\mathrm{str}}^{(i)}(x)$ for all  $x\in[N]$.
$x\in[N]$.
Proof. This is [Reference Chapman and Chow2, lemma 8.3].
Applying this to a given function f allows us to write ![]() $\Phi(f; g)$ as the sum of
$\Phi(f; g)$ as the sum of ![]() $\Phi(f_\mathrm{str} + f_\mathrm{sml}; g)$ and
$\Phi(f_\mathrm{str} + f_\mathrm{sml}; g)$ and ![]() $2^s -1$ terms
$2^s -1$ terms ![]() $\Phi(f_1,\ldots,f_s;g)$, where at least one of the fi equals
$\Phi(f_1,\ldots,f_s;g)$, where at least one of the fi equals ![]() $f_{\mathrm{unf}}$ and the rest are equal to
$f_{\mathrm{unf}}$ and the rest are equal to ![]() $f_{\mathrm{str}}+f_{\mathrm{sml}}$. As is typical in applications of the arithmetic regularity lemma, we expect the term
$f_{\mathrm{str}}+f_{\mathrm{sml}}$. As is typical in applications of the arithmetic regularity lemma, we expect the term ![]() $\Phi(f_{\mathrm{str}}+f_{\mathrm{sml}};g)$ to provide the main contribution, while the remaining terms should be asymptotically negligible. This prediction is verified by combining Property (III) of lemma 8.2 with our Fourier control result (lemma 7.1).
$\Phi(f_{\mathrm{str}}+f_{\mathrm{sml}};g)$ to provide the main contribution, while the remaining terms should be asymptotically negligible. This prediction is verified by combining Property (III) of lemma 8.2 with our Fourier control result (lemma 7.1).
To carry out this strategy of removing the contribution of ![]() $f_\mathrm{unf}$, we need to perform a minor technical manoeuvre. Applying lemma 7.1 requires us to bound the function g appearing in
$f_\mathrm{unf}$, we need to perform a minor technical manoeuvre. Applying lemma 7.1 requires us to bound the function g appearing in ![]() $\Phi(f; g)$ in terms of νD. To achieve a strong asymptotic lower bound for the number of solutions, we desire a bound of the form
$\Phi(f; g)$ in terms of νD. To achieve a strong asymptotic lower bound for the number of solutions, we desire a bound of the form ![]() $g\lVert \nu_D\rVert_{\infty}
\ll \nu_D$. This is the method we used in [Reference Chapman and Chow2, lemma 8.4], only with µD in place of νD. However, this relied on the fact that µD is constant on its support, while νD is not. In particular, if g is the indicator function of a colour class, then
$g\lVert \nu_D\rVert_{\infty}
\ll \nu_D$. This is the method we used in [Reference Chapman and Chow2, lemma 8.4], only with µD in place of νD. However, this relied on the fact that µD is constant on its support, while νD is not. In particular, if g is the indicator function of a colour class, then ![]() $g(z)\lVert \nu_D\rVert_{\infty}$ could be asymptotically larger than
$g(z)\lVert \nu_D\rVert_{\infty}$ could be asymptotically larger than ![]() $\nu_D(z)$ for small z.
$\nu_D(z)$ for small z.
To overcome this issue, we restrict attention from ![]() $[Z]$ to
$[Z]$ to ![]() $[\eta Z, Z]$, for some sufficiently small η > 0. On this latter interval, the function νD does not vary too much. This is made precise by the following lemma, which is a variation of [Reference Chapman and Chow2, lemma 8.12].
$[\eta Z, Z]$, for some sufficiently small η > 0. On this latter interval, the function νD does not vary too much. This is made precise by the following lemma, which is a variation of [Reference Chapman and Chow2, lemma 8.12].
Lemma 8.3. Let P be a real polynomial of degree ![]() $d\in\mathbb{N}$ with positive leading coefficient. Then, there exists a positive integer
$d\in\mathbb{N}$ with positive leading coefficient. Then, there exists a positive integer ![]() $M_0(P)$ such that the following is true. For all
$M_0(P)$ such that the following is true. For all ![]() $\eta\in(0,1)$, if
$\eta\in(0,1)$, if ![]() $x\in\mathbb{R}$ satisfies
$x\in\mathbb{R}$ satisfies ![]() $x\geqslant \eta^{-1}M_{0}(P)$, then
$x\geqslant \eta^{-1}M_{0}(P)$, then
Proof. Let ![]() $\ell_P \gt 0$ be the leading coefficient of P. We can then find
$\ell_P \gt 0$ be the leading coefficient of P. We can then find ![]() $M_0(P)\in\mathbb{N}$ such that
$M_0(P)\in\mathbb{N}$ such that
holds for all real ![]() $x\geqslant M_0(P)$. In particular, if
$x\geqslant M_0(P)$. In particular, if ![]() $x\geqslant \eta^{-1}M_{0}(P)$, then
$x\geqslant \eta^{-1}M_{0}(P)$, then
 \begin{equation*}
\frac{\eta^d}{3} \leqslant \frac{P(\eta x)}{P(x)} \leqslant 3\eta^d.
\end{equation*}
\begin{equation*}
\frac{\eta^d}{3} \leqslant \frac{P(\eta x)}{P(x)} \leqslant 3\eta^d.
\end{equation*}Lemma 8.4. (Removing  $f_{\mathrm{unf}}$)
$f_{\mathrm{unf}}$)
Let ![]() $f:\mathbb{Z}\to[0,1]$ be supported on
$f:\mathbb{Z}\to[0,1]$ be supported on ![]() $[N]$. Let
$[N]$. Let ![]() $\eta,{\sigma} \gt 0$, and let
$\eta,{\sigma} \gt 0$, and let ![]() $\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ be a monotone increasing function. Let
$\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ be a monotone increasing function. Let ![]() $f_{\mathrm{str}},f_{\mathrm{sml}},f_{\mathrm{unf}}$ be the functions obtained upon applying lemma 8.2 to f. Then, for any
$f_{\mathrm{str}},f_{\mathrm{sml}},f_{\mathrm{unf}}$ be the functions obtained upon applying lemma 8.2 to f. Then, for any ![]() $g:\mathbb{Z}\to[0,1]$ supported on the set
$g:\mathbb{Z}\to[0,1]$ supported on the set
we have
 \begin{equation*}
\lvert\Phi(f;g\circ\mathcal Q_Z)-\Phi(f_{\mathrm{str}}+f_{\mathrm{sml}};g\circ\mathcal Q_Z)\rvert\ll_{h,\eta,D} N^{s-1}\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \mathcal F(K)^{-1/(2s+2t)}.
\end{equation*}
\begin{equation*}
\lvert\Phi(f;g\circ\mathcal Q_Z)-\Phi(f_{\mathrm{str}}+f_{\mathrm{sml}};g\circ\mathcal Q_Z)\rvert\ll_{h,\eta,D} N^{s-1}\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \mathcal F(K)^{-1/(2s+2t)}.
\end{equation*}Proof. Note that ![]() $|f|\leqslant 1_{[N]}$ and
$|f|\leqslant 1_{[N]}$ and  $\lVert \hat{f}\rVert_{\infty} \leqslant N$. Thus, by using a telescoping identity, as in the derivation of (7.1), lemma 7.1 informs us that
$\lVert \hat{f}\rVert_{\infty} \leqslant N$. Thus, by using a telescoping identity, as in the derivation of (7.1), lemma 7.1 informs us that
holds for any ![]() $G:\mathbb{Z}\to\mathbb{R}$ such that
$G:\mathbb{Z}\to\mathbb{R}$ such that ![]() $|G|\leqslant \nu_D$. Taking
$|G|\leqslant \nu_D$. Taking ![]() $G=\xi(g\circ\mathcal Q_Z)$ for some ξ > 0, we deduce that
$G=\xi(g\circ\mathcal Q_Z)$ for some ξ > 0, we deduce that
To complete the proof, it remains to find ξ > 0 with ![]() $\xi|g\circ\mathcal Q_Z|\leqslant \nu_D$ such that
$\xi|g\circ\mathcal Q_Z|\leqslant \nu_D$ such that
 \begin{equation*}
N/\xi \ll \frac{DZ}{\varphi(D)\log Z}.
\end{equation*}
\begin{equation*}
N/\xi \ll \frac{DZ}{\varphi(D)\log Z}.
\end{equation*}Set
Observe that, for all ![]() $n=h_D(z)\in B$, we have
$n=h_D(z)\in B$, we have
By lemma 8.3, if Z is sufficiently large relative to h, η, and D, then
Since ![]() $g\circ\mathcal Q_Z$ is supported on B and takes values in
$g\circ\mathcal Q_Z$ is supported on B and takes values in ![]() $[0,1]$, we conclude that there exists
$[0,1]$, we conclude that there exists ![]() $c \gg 1$ such that
$c \gg 1$ such that ![]() $\xi:=c(DZ)^{-1}\varphi(D)N
\log Z$ has all the required properties.
$\xi:=c(DZ)^{-1}\varphi(D)N
\log Z$ has all the required properties.
9. Prime polynomial Bohr sets
The final step of the proof of theorem 8.1 is to obtain a lower bound for the main term ![]() $\Phi(f_{\mathrm{str}}+f_{\mathrm{sml}};g\circ\mathcal Q_Z)$. Using our assumption that the coefficients of L 1 are coprime, Bézout’s lemma provides us with some
$\Phi(f_{\mathrm{str}}+f_{\mathrm{sml}};g\circ\mathcal Q_Z)$. Using our assumption that the coefficients of L 1 are coprime, Bézout’s lemma provides us with some ![]() $\mathbf{v}\in\mathbb{Z}^s$, which depends only on L 1, such that
$\mathbf{v}\in\mathbb{Z}^s$, which depends only on L 1, such that ![]() $L_1(\mathbf{v}) =1$. We can therefore write
$L_1(\mathbf{v}) =1$. We can therefore write
 \begin{equation}
\Phi(f_1,\ldots,f_s;g\circ\mathcal Q_Z) = \sum_{\mathbf{z}\in[\eta Z,Z]^t}g(z_1) \cdots g(z_t)\Psi_{\mathbf{z}}(f_1,\ldots,f_s),
\end{equation}
\begin{equation}
\Phi(f_1,\ldots,f_s;g\circ\mathcal Q_Z) = \sum_{\mathbf{z}\in[\eta Z,Z]^t}g(z_1) \cdots g(z_t)\Psi_{\mathbf{z}}(f_1,\ldots,f_s),
\end{equation}where we have introduced the auxiliary counting operator
 \begin{equation*}
\Psi_{\mathbf{z}}(f_1,\ldots,f_s) := \sum_{L_1({\mathbf{n}})=0}\prod_{i=1}^{s}f_i(n_i + v_iL_2(h_D(\mathbf{z}))).
\end{equation*}
\begin{equation*}
\Psi_{\mathbf{z}}(f_1,\ldots,f_s) := \sum_{L_1({\mathbf{n}})=0}\prod_{i=1}^{s}f_i(n_i + v_iL_2(h_D(\mathbf{z}))).
\end{equation*} Our goal is to show that there is a large supply of ![]() $\mathbf{z}\in\mathbb{Z}^t$ for which
$\mathbf{z}\in\mathbb{Z}^t$ for which ![]() $\Psi_\mathbf{z}(f_\mathrm{str} + f_\mathrm{sml})$ is asymptotically as large as possible. This is accomplished by choosing the zi to lie in a set of ‘almost-periods’ for
$\Psi_\mathbf{z}(f_\mathrm{str} + f_\mathrm{sml})$ is asymptotically as large as possible. This is accomplished by choosing the zi to lie in a set of ‘almost-periods’ for ![]() $f_\mathrm{str}$. These are known as polynomial Bohr sets and take the form
$f_\mathrm{str}$. These are known as polynomial Bohr sets and take the form
 \begin{equation*}
\{n\in\mathbb{N}:\lVert Q(n)\boldsymbol{{\alpha}}\rVert \lt \rho\}
=\bigcap_{i=1}^{K}
\{n\in\mathbb{N}: \lVert Q(n)\alpha_{i}\rVert \lt \rho\},
\end{equation*}
\begin{equation*}
\{n\in\mathbb{N}:\lVert Q(n)\boldsymbol{{\alpha}}\rVert \lt \rho\}
=\bigcap_{i=1}^{K}
\{n\in\mathbb{N}: \lVert Q(n)\alpha_{i}\rVert \lt \rho\},
\end{equation*} for some ρ > 0, ![]() $K\in\mathbb{N}$,
$K\in\mathbb{N}$, ![]() $\boldsymbol{{\alpha}}\in\mathbb{T}^K$, and
$\boldsymbol{{\alpha}}\in\mathbb{T}^K$, and ![]() $Q(x) \in \mathbb{Z}[x]$.
$Q(x) \in \mathbb{Z}[x]$.
Lemma 9.1. (Lower bound for  $\Psi_{\mathbf{z}}(f_{\mathrm{str}}+f_{\mathrm{sml}})$)
$\Psi_{\mathbf{z}}(f_{\mathrm{str}}+f_{\mathrm{sml}})$)
For all δ > 0, there exist positive constants ![]() $c_{1}(\delta)=c_{1}(L_1,L_2;\delta)$ and
$c_{1}(\delta)=c_{1}(L_1,L_2;\delta)$ and ![]() $\eta_0 = \eta_0(d,L_1,L_2,\delta) \lt 1$ such that the following is true. Suppose
$\eta_0 = \eta_0(d,L_1,L_2,\delta) \lt 1$ such that the following is true. Suppose ![]() $f:\mathbb{Z}\to[0,1]$ is supported on
$f:\mathbb{Z}\to[0,1]$ is supported on ![]() $[N]$ and satisfies
$[N]$ and satisfies ![]() $\lVert f\rVert_1\geqslant \delta N$. Given
$\lVert f\rVert_1\geqslant \delta N$. Given ![]() ${\sigma} \in (0,1]$ and a monotone increasing function
${\sigma} \in (0,1]$ and a monotone increasing function ![]() $\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$, let
$\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$, let ![]() $f_{\mathrm{str}}$,
$f_{\mathrm{str}}$, ![]() $f_{\mathrm{sml}}$, K, and θ be as given by applying lemma 8.2 to f. If
$f_{\mathrm{sml}}$, K, and θ be as given by applying lemma 8.2 to f. If ![]() $\mathbf{z}\in[\eta_0 Z]^{t}$ satisfies
$\mathbf{z}\in[\eta_0 Z]^{t}$ satisfies
then
 \begin{equation*}
\Psi_{\mathbf{z}}(f_{\mathrm{str}}+f_{\mathrm{sml}}) \geqslant \left(c_{1}(\delta)- O_{L_1,L_2}({\sigma})\right)N^{s-1}.
\end{equation*}
\begin{equation*}
\Psi_{\mathbf{z}}(f_{\mathrm{str}}+f_{\mathrm{sml}}) \geqslant \left(c_{1}(\delta)- O_{L_1,L_2}({\sigma})\right)N^{s-1}.
\end{equation*} In particular, if σ is sufficiently small relative to ![]() $(d,L_1,L_2,\delta)$, then
$(d,L_1,L_2,\delta)$, then
 \begin{equation*}
\Psi_{\mathbf{z}}(f_{\mathrm{str}}+f_{\mathrm{sml}}) \gg_{L_1,L_2,\delta}N^{s-1}.
\end{equation*}
\begin{equation*}
\Psi_{\mathbf{z}}(f_{\mathrm{str}}+f_{\mathrm{sml}}) \gg_{L_1,L_2,\delta}N^{s-1}.
\end{equation*}Proof. This is [Reference Chapman and Chow2, lemma 8.13] with ![]() $\rho=\sigma/K$.
$\rho=\sigma/K$.
Recall that we seek solutions to the linearized equation (2.7) with ![]() $r_D + Dz_j$ prime for all j. In view of lemma 9.1, we are therefore interested in sets of the form
$r_D + Dz_j$ prime for all j. In view of lemma 9.1, we are therefore interested in sets of the form
The main purpose of this section is to establish the following density bounds for these prime polynomial Bohr sets.
Theorem 9.2 Let ![]() $K,D,d\in\mathbb{N}$,
$K,D,d\in\mathbb{N}$, ![]() $0 \lt \rho\leqslant 1$, and let h be an integer polynomial of degree d which is intersective of the second kind. Then, there exists a positive integer
$0 \lt \rho\leqslant 1$, and let h be an integer polynomial of degree d which is intersective of the second kind. Then, there exists a positive integer ![]() $P_1=P_1(D,h,K,\rho)$ and a positive real number
$P_1=P_1(D,h,K,\rho)$ and a positive real number ![]() $\Delta(\rho)=\Delta(h,K;\rho)\leqslant 1$ such that the following is true for all
$\Delta(\rho)=\Delta(h,K;\rho)\leqslant 1$ such that the following is true for all ![]() $P\geqslant P_1$. If
$P\geqslant P_1$. If ![]() $\boldsymbol{{\alpha}}\in\mathbb{T}^K$, then
$\boldsymbol{{\alpha}}\in\mathbb{T}^K$, then
 \begin{equation*}
\sum_{p\in\mathcal B}\log p \geqslant\frac{\Delta(\rho)P}{\varphi(D)},
\end{equation*}
\begin{equation*}
\sum_{p\in\mathcal B}\log p \geqslant\frac{\Delta(\rho)P}{\varphi(D)},
\end{equation*} where ![]() $\mathcal B=[P]\cap\mathcal B_h(\boldsymbol{\alpha},\rho)$. Moreover, we may take
$\mathcal B=[P]\cap\mathcal B_h(\boldsymbol{\alpha},\rho)$. Moreover, we may take
 \begin{align*}
\Delta(h,1;\rho) &\gg_{h,\varepsilon} \rho^{d+3+\varepsilon}, \\ \Delta(h,K;\rho)
&\gg_{h,K, \varepsilon} \:
\rho^{3 + K(d+\varepsilon)} \Delta\left(h,K-1;\frac{\rho^{2}}{2K^2}\right) \quad (K \gt 1).
\end{align*}
\begin{align*}
\Delta(h,1;\rho) &\gg_{h,\varepsilon} \rho^{d+3+\varepsilon}, \\ \Delta(h,K;\rho)
&\gg_{h,K, \varepsilon} \:
\rho^{3 + K(d+\varepsilon)} \Delta\left(h,K-1;\frac{\rho^{2}}{2K^2}\right) \quad (K \gt 1).
\end{align*}We demonstrate the utility of this result by using it to complete the proof of theorem 8.1.
Proof of theorem 8.1 given theorem 9.2
As usual, we fix the parameters
appearing in the statement of theorem 8.1. Unless specified otherwise, we allow all forthcoming implicit constants to depend implicitly on these parameters. Let ![]() ${\sigma},\eta\in(0,1)$ and let
${\sigma},\eta\in(0,1)$ and let ![]() $\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ be a monotone increasing function, all three of which depend only on the fixed parameters. Let
$\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ be a monotone increasing function, all three of which depend only on the fixed parameters. Let ![]() $D\in\mathbb{N}$, and assume throughout this proof that
$D\in\mathbb{N}$, and assume throughout this proof that ![]() $Z\in\mathbb{N}$ and
$Z\in\mathbb{N}$ and ![]() $N:=h_D(Z)$ are sufficiently large with respect to all of these quantities.
$N:=h_D(Z)$ are sufficiently large with respect to all of these quantities.
For each ![]() $i\in[r]$, let
$i\in[r]$, let ![]() $\mathcal A_i\subseteq [N]$ with
$\mathcal A_i\subseteq [N]$ with ![]() $|\mathcal A_i|\geqslant\delta N$. Suppose we have an r-colouring
$|\mathcal A_i|\geqslant\delta N$. Suppose we have an r-colouring
In the notation of the previous section, our goal is to find ![]() $k\in\mathbb{N}$ such that
$k\in\mathbb{N}$ such that
 \begin{equation*}
\Phi(1_{\mathcal A_i};1_{\mathcal C_k}\circ\mathcal Q_Z) \gg
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \qquad(1\leqslant i\leqslant r).
\end{equation*}
\begin{equation*}
\Phi(1_{\mathcal A_i};1_{\mathcal C_k}\circ\mathcal Q_Z) \gg
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \qquad(1\leqslant i\leqslant r).
\end{equation*}Lemma 8.2 provides us with decompositions
 \begin{equation*}
1_{\mathcal A_i} = f_\mathrm{str}^{(i)} + f_\mathrm{sml}^{(i)} + f_\mathrm{unf}^{(i)} \qquad (1\leqslant i\leqslant r),
\end{equation*}
\begin{equation*}
1_{\mathcal A_i} = f_\mathrm{str}^{(i)} + f_\mathrm{sml}^{(i)} + f_\mathrm{unf}^{(i)} \qquad (1\leqslant i\leqslant r),
\end{equation*} along with a positive integer ![]() $K\ll_{\sigma,\mathcal F} 1$ and a phase
$K\ll_{\sigma,\mathcal F} 1$ and a phase ![]() $\boldsymbol{\theta}\in\mathbb{T}^K$ with the properties described therein. Let
$\boldsymbol{\theta}\in\mathbb{T}^K$ with the properties described therein. Let ![]() $\eta_0=\eta_0(d,L_1,L_2,\delta)$ be as defined in lemma 9.1, and let
$\eta_0=\eta_0(d,L_1,L_2,\delta)$ be as defined in lemma 9.1, and let
By choosing σ sufficiently small, lemma 9.1 and (9.1) inform us that
 \begin{equation*}
\Phi(f_\mathrm{str}^{(i)}+f_\mathrm{sml}^{(i)}; 1_{\mathcal C_j}\circ\mathcal Q_Z) \gg N^{s-1}|\Omega\cap\mathcal C_j|^t \qquad (1\leqslant i,j\leqslant r).
\end{equation*}
\begin{equation*}
\Phi(f_\mathrm{str}^{(i)}+f_\mathrm{sml}^{(i)}; 1_{\mathcal C_j}\circ\mathcal Q_Z) \gg N^{s-1}|\Omega\cap\mathcal C_j|^t \qquad (1\leqslant i,j\leqslant r).
\end{equation*} We now claim that, for an appropriate choice of ![]() $\eta \lt \eta_0$, the set Ω satisfies
$\eta \lt \eta_0$, the set Ω satisfies
 \begin{equation}
|\Omega| \gg_K \frac{DZ}{\varphi(D)\log Z}.
\end{equation}
\begin{equation}
|\Omega| \gg_K \frac{DZ}{\varphi(D)\log Z}.
\end{equation} Assume for the moment that this is true. By the pigeonhole principle, we can choose ![]() $k\in[r]$ such that
$k\in[r]$ such that ![]() $r|\Omega\cap\mathcal C_k|\geqslant|\Omega|$, whence
$r|\Omega\cap\mathcal C_k|\geqslant|\Omega|$, whence
 \begin{equation*}
\Phi(f_\mathrm{str}^{(i)}+f_\mathrm{sml}^{(i)}; 1_{\mathcal C_k}\circ\mathcal Q_Z) \gg_K
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \qquad (1\leqslant i\leqslant r).
\end{equation*}
\begin{equation*}
\Phi(f_\mathrm{str}^{(i)}+f_\mathrm{sml}^{(i)}; 1_{\mathcal C_k}\circ\mathcal Q_Z) \gg_K
N^{s-1}
\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \qquad (1\leqslant i\leqslant r).
\end{equation*}Incorporating lemma 8.4 furnishes the bound
 \begin{equation*}
\Phi(1_{\mathcal A_i};1_{\mathcal C_k}\circ\mathcal Q_Z) \gg N^{s-1}\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \left(c(K) - \mathcal F(K)^{-1/(2s+2t)}\right),
\end{equation*}
\begin{equation*}
\Phi(1_{\mathcal A_i};1_{\mathcal C_k}\circ\mathcal Q_Z) \gg N^{s-1}\left(\frac{DZ}{\varphi(D)\log Z} \right)^t \left(c(K) - \mathcal F(K)^{-1/(2s+2t)}\right),
\end{equation*} for some positively-valued function ![]() $c(K) \gt 0$ whose value depends only on the fixed parameters and K. Specifying
$c(K) \gt 0$ whose value depends only on the fixed parameters and K. Specifying ![]() $\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ to be a monotone increasing function which obeys
$\mathcal F:\mathbb{R}_{\geqslant 0}\to\mathbb{R}_{\geqslant 0}$ to be a monotone increasing function which obeys
then finishes the proof of theorem 8.1, subject to our claim.
It remains to establish (9.3). Let
Let ![]() $\rho=\sigma/K$, and for each
$\rho=\sigma/K$, and for each ![]() $\xi\in(0,1)$ put
$\xi\in(0,1)$ put
 \begin{align*}
\mathcal D_\xi &= \mathcal P\cap\{p\in[\xi P,P]:p\equiv r_D\;(\operatorname{mod}{D}), \;\lVert \boldsymbol{\theta} h(p)/{\lambda}(D) \rVert \lt \rho \} \\ &= [\xi P,P]\cap\mathcal B_h(\boldsymbol{\theta},\rho).
\end{align*}
\begin{align*}
\mathcal D_\xi &= \mathcal P\cap\{p\in[\xi P,P]:p\equiv r_D\;(\operatorname{mod}{D}), \;\lVert \boldsymbol{\theta} h(p)/{\lambda}(D) \rVert \lt \rho \} \\ &= [\xi P,P]\cap\mathcal B_h(\boldsymbol{\theta},\rho).
\end{align*} By theorem 9.2 and the Siegel-Walfisz theorem, there exists ![]() $\xi\in(0,1)$ with
$\xi\in(0,1)$ with ![]() $\xi\gg\Delta(\rho)$ such that
$\xi\gg\Delta(\rho)$ such that
 \begin{equation*}
\sum_{p\in\mathcal D_\xi}\log p \geqslant \frac{\Delta(\rho)P}{2\varphi(D)} \gg_\rho \frac{P}{\varphi(D)}.
\end{equation*}
\begin{equation*}
\sum_{p\in\mathcal D_\xi}\log p \geqslant \frac{\Delta(\rho)P}{2\varphi(D)} \gg_\rho \frac{P}{\varphi(D)}.
\end{equation*} Choosing ![]() $\eta = \eta_0\xi/2$, we ensure that the injective function
$\eta = \eta_0\xi/2$, we ensure that the injective function ![]() $y\mapsto (y-r_D)/D$ maps
$y\mapsto (y-r_D)/D$ maps ![]() $[\xi P,P]$ into
$[\xi P,P]$ into ![]() $[\eta Z, \eta_0 Z]\subseteq [\eta Z, Z]$ and maps
$[\eta Z, \eta_0 Z]\subseteq [\eta Z, Z]$ and maps ![]() $\mathcal D_\xi$ into Ω. Since
$\mathcal D_\xi$ into Ω. Since ![]() $\rho=O_K(1)$, we therefore conclude that
$\rho=O_K(1)$, we therefore conclude that
 \begin{equation*}
|\Omega|\geqslant \sum_{p\in\mathcal D_\xi}
\frac{\log p}{\log P} \gg_K \frac{DZ}{\varphi(D)\log Z},
\end{equation*}
\begin{equation*}
|\Omega|\geqslant \sum_{p\in\mathcal D_\xi}
\frac{\log p}{\log P} \gg_K \frac{DZ}{\varphi(D)\log Z},
\end{equation*}as claimed.
9.1. Exponential sums
To study prime polynomial Bohr sets, we are interested in exponential sums over primes of the form
 \begin{equation*}
\sum_{\substack{p \leqslant P \\
p \equiv r_D \;(\operatorname{mod}{D})}}
e \left(
\frac{h(p) \theta}{{\lambda}(D)} \right) \log p,
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P \\
p \equiv r_D \;(\operatorname{mod}{D})}}
e \left(
\frac{h(p) \theta}{{\lambda}(D)} \right) \log p,
\end{equation*} where ![]() $\theta\in\mathbb{T}$ and h is intersective of the second kind. Lê and Spencer [Reference Lê and Spencer14] analysed properties of sums of this form to obtain estimates for the smallest element of a prime polynomial Bohr set (9.2), showing in particular that these sets are always non-empty. Our goal is to obtain a lower bound for the densities of these Bohr sets which does not depend on the choice of phase α.
$\theta\in\mathbb{T}$ and h is intersective of the second kind. Lê and Spencer [Reference Lê and Spencer14] analysed properties of sums of this form to obtain estimates for the smallest element of a prime polynomial Bohr set (9.2), showing in particular that these sets are always non-empty. Our goal is to obtain a lower bound for the densities of these Bohr sets which does not depend on the choice of phase α.
Following [Reference Lê and Spencer14], our argument begins with the observation that if the prime polynomial Bohr set (9.2) has few elements, then we can construct a corresponding exponential sum which is particularly large. This is elucidated by the following lemma, which is a consequence of a much more general result of Harman [Reference Harman8].
Lemma 9.3. Let ![]() $D,K,P\in\mathbb{N}$. Let h be an integer polynomial of degree
$D,K,P\in\mathbb{N}$. Let h be an integer polynomial of degree ![]() $d\in\mathbb{N}$ which is intersective of the second kind. Define rD and
$d\in\mathbb{N}$ which is intersective of the second kind. Define rD and ![]() $\lambda(D)$ as in §2.4. Let
$\lambda(D)$ as in §2.4. Let ![]() $\rho\in (0,1)$,
$\rho\in (0,1)$, ![]() $\boldsymbol{\alpha}\in\mathbb{T}^K$, and
$\boldsymbol{\alpha}\in\mathbb{T}^K$, and
 \begin{equation*}
\mathcal C = \mathcal C_h(\boldsymbol{\alpha},\rho):= \mathcal P\cap\left \{p \leqslant P: p \equiv r_D \;(\operatorname{mod}{D}),
\left \| \frac{h(p)}{{\lambda}(D)} \boldsymbol{{\alpha}} \right \| \geqslant \rho \right \}.
\end{equation*}
\begin{equation*}
\mathcal C = \mathcal C_h(\boldsymbol{\alpha},\rho):= \mathcal P\cap\left \{p \leqslant P: p \equiv r_D \;(\operatorname{mod}{D}),
\left \| \frac{h(p)}{{\lambda}(D)} \boldsymbol{{\alpha}} \right \| \geqslant \rho \right \}.
\end{equation*} Then, there exists ![]() $\mathbf{m}\in\mathbb{Z}^K$ with
$\mathbf{m}\in\mathbb{Z}^K$ with ![]() $0 \lt \lVert \mathbf{m}\rVert_{\infty} \leqslant K\rho^{-1}$ such that
$0 \lt \lVert \mathbf{m}\rVert_{\infty} \leqslant K\rho^{-1}$ such that
 \begin{equation*}
(2K + 1)^K\left\lvert
\sum_{p\in\mathcal C}
e \left(\frac{h(p) \mathbf{m}\cdot\boldsymbol{\alpha}}{{\lambda}(D)} \right)
\log p\right\rvert \geqslant \frac{\rho^K}{4K^2 - 1}
\sum_{p\in\mathcal C}\log p.
\end{equation*}
\begin{equation*}
(2K + 1)^K\left\lvert
\sum_{p\in\mathcal C}
e \left(\frac{h(p) \mathbf{m}\cdot\boldsymbol{\alpha}}{{\lambda}(D)} \right)
\log p\right\rvert \geqslant \frac{\rho^K}{4K^2 - 1}
\sum_{p\in\mathcal C}\log p.
\end{equation*}Proof. If ![]() $\rho \gt 1/2$, then
$\rho \gt 1/2$, then ![]() $\mathcal C$ is empty and both sides of the desired inequality equal zero. If
$\mathcal C$ is empty and both sides of the desired inequality equal zero. If ![]() $\rho \leqslant 1/2$, then the result follows from the contrapositive of [Reference Harman8, corollary to lemma 5] and the pigeonhole principle.
$\rho \leqslant 1/2$, then the result follows from the contrapositive of [Reference Harman8, corollary to lemma 5] and the pigeonhole principle.
For the purpose of proving theorem 9.2, we may assume that the Bohr set ![]() $\mathcal B_h(\boldsymbol{\alpha},\rho)$ has too few elements, in a manner that will be clarified in due course. Then we can apply lemma 9.3 to find some
$\mathcal B_h(\boldsymbol{\alpha},\rho)$ has too few elements, in a manner that will be clarified in due course. Then we can apply lemma 9.3 to find some ![]() $L\ll_K \rho^{-K}$ and
$L\ll_K \rho^{-K}$ and ![]() $\mathbf{m}\in\mathbb{Z}^K$ of bounded size such that
$\mathbf{m}\in\mathbb{Z}^K$ of bounded size such that ![]() $\theta = \mathbf{m}\cdot\boldsymbol{\alpha}$ satisfies
$\theta = \mathbf{m}\cdot\boldsymbol{\alpha}$ satisfies
 \begin{equation}
\left|
\sum_{\substack{p \leqslant P \\
p \equiv r_D \;(\operatorname{mod}{D})}}
e \left(
\frac{h(p) \theta}{{\lambda}(D)} \right) \log p \right|
\geqslant \frac{P}{L\varphi(D)}.
\end{equation}
\begin{equation}
\left|
\sum_{\substack{p \leqslant P \\
p \equiv r_D \;(\operatorname{mod}{D})}}
e \left(
\frac{h(p) \theta}{{\lambda}(D)} \right) \log p \right|
\geqslant \frac{P}{L\varphi(D)}.
\end{equation}Our next task is to investigate the consequences of (9.4). As discussed in §4, an exponential sum being large is indicative of the phase θ exhibiting ‘major arc’ behaviour, meaning that θ is well-approximated by a rational number with small denominator. This is made precise in the following lemma.
Lemma 9.4. (Low major arc)
Suppose ![]() $L,P\in\mathbb{N}$ and
$L,P\in\mathbb{N}$ and ![]() $\theta\in\mathbb{R}$ satisfy (9.4). Assume that P is sufficiently large relative to
$\theta\in\mathbb{R}$ satisfy (9.4). Assume that P is sufficiently large relative to ![]() $D,h$ and L. Then, there exists
$D,h$ and L. Then, there exists ![]() $q \in \mathbb{N}$ such that
$q \in \mathbb{N}$ such that
 \begin{equation*}
q \ll_{h,\varepsilon} L^{d+\varepsilon},
\qquad \| q\theta \| \ll_h qL^d {\lambda}(D) / P^d.
\end{equation*}
\begin{equation*}
q \ll_{h,\varepsilon} L^{d+\varepsilon},
\qquad \| q\theta \| \ll_h qL^d {\lambda}(D) / P^d.
\end{equation*}Proof. By (9.4) and lemma 4.2, we can find ![]() $r\in\mathbb{N}$ and
$r\in\mathbb{N}$ and ![]() $b\in\mathbb{Z}$ such that
$b\in\mathbb{Z}$ such that
 \begin{equation*}
\max \left \{r, P^d
\left|
r \frac{\theta}
{{\lambda}(D)} - b
\right|
\right \}
\ll (\log P)^{2 C_d}.
\end{equation*}
\begin{equation*}
\max \left \{r, P^d
\left|
r \frac{\theta}
{{\lambda}(D)} - b
\right|
\right \}
\ll (\log P)^{2 C_d}.
\end{equation*} Let ![]() $q \in \mathbb{N}$ and
$q \in \mathbb{N}$ and ![]() $a \in \mathbb{Z}$ with
$a \in \mathbb{Z}$ with
 \begin{equation*}
(a,q) = 1, \qquad
\frac{{\lambda}(D) b}{r} =
\frac a q.
\end{equation*}
\begin{equation*}
(a,q) = 1, \qquad
\frac{{\lambda}(D) b}{r} =
\frac a q.
\end{equation*}Then
 \begin{equation*}
q \leqslant r \ll
(\log P)^{2 C_d}, \qquad
|q \theta - a| \leqslant
|r \theta -
{\lambda}(D) b| \ll
\frac{{\lambda}(D) (\log P)^{2C_d}} {P^d}.
\end{equation*}
\begin{equation*}
q \leqslant r \ll
(\log P)^{2 C_d}, \qquad
|q \theta - a| \leqslant
|r \theta -
{\lambda}(D) b| \ll
\frac{{\lambda}(D) (\log P)^{2C_d}} {P^d}.
\end{equation*} Put ![]() ${\beta} = \theta - a/q$. Applying lemma 4.3 with
${\beta} = \theta - a/q$. Applying lemma 4.3 with ![]() $(f,G,b,m,Q)
= (h, 1, r_D, D, \lambda(D))$ gives
$(f,G,b,m,Q)
= (h, 1, r_D, D, \lambda(D))$ gives
 \begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv r_D \;(\operatorname{mod}{D})}} e \left(
\frac{\theta h(p)}{{\lambda}(D)} \right) \log p = I({\beta}) \frac{S(q,a;D)}{\varphi(Dq)} +
O_h(Pe^{-c \sqrt{\log P}}),
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P \\ p \equiv r_D \;(\operatorname{mod}{D})}} e \left(
\frac{\theta h(p)}{{\lambda}(D)} \right) \log p = I({\beta}) \frac{S(q,a;D)}{\varphi(Dq)} +
O_h(Pe^{-c \sqrt{\log P}}),
\end{equation*}where
 \begin{equation*}
I({\beta}) = \int_2^P e\left(
\frac{{\beta} h(t)}{{\lambda}(D)}\right) {\,{\rm d}} t,
\qquad
S(q,a;D) = \sum_{\substack{t \;(\operatorname{mod}{Dq}) \\ (t,q) = 1 \\ t \equiv r_D \;(\operatorname{mod}{D})}} e \left(
\frac{a h(t)}
{q{\lambda}(D)}
\right).
\end{equation*}
\begin{equation*}
I({\beta}) = \int_2^P e\left(
\frac{{\beta} h(t)}{{\lambda}(D)}\right) {\,{\rm d}} t,
\qquad
S(q,a;D) = \sum_{\substack{t \;(\operatorname{mod}{Dq}) \\ (t,q) = 1 \\ t \equiv r_D \;(\operatorname{mod}{D})}} e \left(
\frac{a h(t)}
{q{\lambda}(D)}
\right).
\end{equation*}Thus, by (9.4), we have
 \begin{equation}
|S(q,a;D) I({\beta})|
\gg \frac{P \varphi(Dq)}{L \varphi(D)}.
\end{equation}
\begin{equation}
|S(q,a;D) I({\beta})|
\gg \frac{P \varphi(Dq)}{L \varphi(D)}.
\end{equation} In light of the trivial bound ![]() $|I(\beta)|\leqslant P$, we now have
$|I(\beta)|\leqslant P$, we now have
 \begin{equation*}
|S(q,a;D)| \gg \frac{\varphi(Dq)}{L \varphi(D)} \geqslant \frac{\varphi(q)}{L}.
\end{equation*}
\begin{equation*}
|S(q,a;D)| \gg \frac{\varphi(Dq)}{L \varphi(D)} \geqslant \frac{\varphi(q)}{L}.
\end{equation*}By [Reference Lucier15, lemma 28], the GCD of the non-constant coefficients of
 \begin{equation*}
h_D(x) := \frac{h(r_D + Dx)}{{\lambda}(D)} \in \mathbb{Z}[x]
\end{equation*}
\begin{equation*}
h_D(x) := \frac{h(r_D + Dx)}{{\lambda}(D)} \in \mathbb{Z}[x]
\end{equation*} is ![]() $O_h(1)$. Now lemma 2.2 yields
$O_h(1)$. Now lemma 2.2 yields
 \begin{equation*}
S(q,a;D) \ll_{h,\varepsilon} q^{1+\varepsilon-1/d},
\end{equation*}
\begin{equation*}
S(q,a;D) \ll_{h,\varepsilon} q^{1+\varepsilon-1/d},
\end{equation*}and we conclude that
 \begin{equation*}
q \ll_{h,\varepsilon} L^{d+\varepsilon}.
\end{equation*}
\begin{equation*}
q \ll_{h,\varepsilon} L^{d+\varepsilon}.
\end{equation*} It remains to bound ![]() $\lVert q\theta\rVert$.
$\lVert q\theta\rVert$.
Observe that
 \begin{align*}
\psi: (\mathbb{Z}/Dq\mathbb{Z})^\times &\to (\mathbb{Z}/D\mathbb{Z})^\times \\
[t] &\mapsto [t]
\end{align*}
\begin{align*}
\psi: (\mathbb{Z}/Dq\mathbb{Z})^\times &\to (\mathbb{Z}/D\mathbb{Z})^\times \\
[t] &\mapsto [t]
\end{align*} defines a surjective group homomorphism, and that ![]() $\psi^{-1}(r_D)$ is a coset of
$\psi^{-1}(r_D)$ is a coset of ![]() $\ker(\psi) \leqslant (\mathbb{Z}/Dq\mathbb{Z})^\times$. Therefore,
$\ker(\psi) \leqslant (\mathbb{Z}/Dq\mathbb{Z})^\times$. Therefore,
 \begin{align*} |S(q,a;D)| &\leqslant
|\psi^{-1}(r_D)| = |\ker(\psi)| =
\frac{\varphi(Dq)}{\varphi(D)}.
\end{align*}
\begin{align*} |S(q,a;D)| &\leqslant
|\psi^{-1}(r_D)| = |\ker(\psi)| =
\frac{\varphi(Dq)}{\varphi(D)}.
\end{align*}Pairing this with (9.5) yields
A change of variables gives
 \begin{equation*}
I({\beta}) = D \int_0^{P/D}
e({\beta} h_D(z)) {\,{\rm d}} z + O(D),
\end{equation*}
\begin{equation*}
I({\beta}) = D \int_0^{P/D}
e({\beta} h_D(z)) {\,{\rm d}} z + O(D),
\end{equation*}and now [Reference Vaughan22, theorem 7.3] yields
Consequently,
and finally,
9.2. Proof of theorem 9.2
Let ![]() $K\in\mathbb{N}$. Writing
$K\in\mathbb{N}$. Writing ![]() $\mathcal B=\mathcal B_h(\boldsymbol{\alpha},\rho)$ and
$\mathcal B=\mathcal B_h(\boldsymbol{\alpha},\rho)$ and ![]() $\mathcal C=\mathcal C_h(\boldsymbol{\alpha},\rho)$, we deduce from the Siegel–Walfisz theorem (theorem 2.1) that
$\mathcal C=\mathcal C_h(\boldsymbol{\alpha},\rho)$, we deduce from the Siegel–Walfisz theorem (theorem 2.1) that
 \begin{equation*}
\sum_{p \in \mathcal B} \log p + \sum_{p \in \mathcal C} \log p = \sum_{\substack{p \leqslant P \\
p \equiv r_D \;(\operatorname{mod}{D})}}\log p \asymp \frac{P}{\varphi(D)}.
\end{equation*}
\begin{equation*}
\sum_{p \in \mathcal B} \log p + \sum_{p \in \mathcal C} \log p = \sum_{\substack{p \leqslant P \\
p \equiv r_D \;(\operatorname{mod}{D})}}\log p \asymp \frac{P}{\varphi(D)}.
\end{equation*} Suppose ![]() $\boldsymbol{\alpha}\in\mathbb{T}^K$ is such that
$\boldsymbol{\alpha}\in\mathbb{T}^K$ is such that
 \begin{equation*}
\sum_{p \in \mathcal B} \log p \leqslant\frac{c(K)\rho^K P}{\varphi(D)},
\end{equation*}
\begin{equation*}
\sum_{p \in \mathcal B} \log p \leqslant\frac{c(K)\rho^K P}{\varphi(D)},
\end{equation*} for some suitably small ![]() $c(K) \gt 0$. If no such α were to exist, then theorem 9.2 would hold with
$c(K) \gt 0$. If no such α were to exist, then theorem 9.2 would hold with ![]() $\Delta(h,K,\rho)\gg_K \rho^K$ which, since we demand that
$\Delta(h,K,\rho)\gg_K \rho^K$ which, since we demand that ![]() $\Delta(h,K,\rho)\leqslant 1$, is stronger than the bound we require. For this choice of α, we infer from lemma 9.3 the existence of some
$\Delta(h,K,\rho)\leqslant 1$, is stronger than the bound we require. For this choice of α, we infer from lemma 9.3 the existence of some ![]() $\mathbf{m}\in\mathbb{Z}^K$ with
$\mathbf{m}\in\mathbb{Z}^K$ with ![]() $0 \lt \lVert \mathbf{m}\rVert_{\infty}\leqslant K\rho^{-1}$ such that
$0 \lt \lVert \mathbf{m}\rVert_{\infty}\leqslant K\rho^{-1}$ such that
 \begin{equation*}
\left\lvert
\sum_{p\in\mathcal C}
e \left(\frac{h(p) \mathbf{m}\cdot\boldsymbol{\alpha}}{{\lambda}(D)} \right)
\log p\right\rvert \gg_K \frac{\rho^K P}{\varphi(D)}.
\end{equation*}
\begin{equation*}
\left\lvert
\sum_{p\in\mathcal C}
e \left(\frac{h(p) \mathbf{m}\cdot\boldsymbol{\alpha}}{{\lambda}(D)} \right)
\log p\right\rvert \gg_K \frac{\rho^K P}{\varphi(D)}.
\end{equation*}We also have
 \begin{equation*}
\left\lvert
\sum_{p\in\mathcal B}
e \left(\frac{h(p) \mathbf{m}\cdot\boldsymbol{\alpha}}{{\lambda}(D)} \right)
\log p\right\rvert \leqslant \sum_{p\in\mathcal B}\log p
\ll \frac{c(K)\rho^K P}{\varphi(D)}.
\end{equation*}
\begin{equation*}
\left\lvert
\sum_{p\in\mathcal B}
e \left(\frac{h(p) \mathbf{m}\cdot\boldsymbol{\alpha}}{{\lambda}(D)} \right)
\log p\right\rvert \leqslant \sum_{p\in\mathcal B}\log p
\ll \frac{c(K)\rho^K P}{\varphi(D)}.
\end{equation*} Choosing c(K) sufficiently small, the triangle inequality furnishes some ![]() $L\ll_K \rho^{-K}$ such that (9.4) holds with
$L\ll_K \rho^{-K}$ such that (9.4) holds with ![]() $\theta=\mathbf{m}\cdot\boldsymbol{\alpha}$. By increasing the value of L if necessary—which only weakens the bound (9.4) that we have obtained—we may assume that
$\theta=\mathbf{m}\cdot\boldsymbol{\alpha}$. By increasing the value of L if necessary—which only weakens the bound (9.4) that we have obtained—we may assume that ![]() $L = C\rho^{-K}$ for some suitably large constant
$L = C\rho^{-K}$ for some suitably large constant ![]() $C=C(h,K) \gt K$ to be specified later. Applying lemma 9.4 supplies us with some
$C=C(h,K) \gt K$ to be specified later. Applying lemma 9.4 supplies us with some ![]() $q\in\mathbb{N}$ such that
$q\in\mathbb{N}$ such that
 \begin{equation}
q \ll_{h,\varepsilon} L^{d+\varepsilon},
\qquad \| q\mathbf{m} \cdot\boldsymbol{\alpha} \| \ll \frac{qL^d {\lambda}(D)}
{P^d}.
\end{equation}
\begin{equation}
q \ll_{h,\varepsilon} L^{d+\varepsilon},
\qquad \| q\mathbf{m} \cdot\boldsymbol{\alpha} \| \ll \frac{qL^d {\lambda}(D)}
{P^d}.
\end{equation} To complete the proof, beginning from the above deductions, we proceed by induction on K. First, suppose that K = 1 and write ![]() $m\in\mathbb{Z}$ in place of
$m\in\mathbb{Z}$ in place of ![]() $\mathbf{m}\in\mathbb{Z}^K$. As h is intersective of the second kind, any integer
$\mathbf{m}\in\mathbb{Z}^K$. As h is intersective of the second kind, any integer ![]() $n \equiv r_{qmD} \;(\operatorname{mod}{qmD})$ satisfies
$n \equiv r_{qmD} \;(\operatorname{mod}{qmD})$ satisfies
Further, by the Siegel–Walfisz theorem and (9.6), we have
 \begin{equation*}
\sum_{\substack{p \leqslant P/L^2
\\ p \equiv r_{qmD}
\;(\operatorname{mod}{qmD})}} \log p \asymp
\frac{P/L^2}{\varphi(qmD)}
\gg_{h,\varepsilon} \frac{P}{L^{d+3+\varepsilon} \varphi(D)}.
\end{equation*}
\begin{equation*}
\sum_{\substack{p \leqslant P/L^2
\\ p \equiv r_{qmD}
\;(\operatorname{mod}{qmD})}} \log p \asymp
\frac{P/L^2}{\varphi(qmD)}
\gg_{h,\varepsilon} \frac{P}{L^{d+3+\varepsilon} \varphi(D)}.
\end{equation*} Since ![]() $r_{qmD} \equiv r_D \;(\operatorname{mod}{D})$, every prime p appearing in the sum on the left is congruent to rD modulo D. Using (2.5), we have
$r_{qmD} \equiv r_D \;(\operatorname{mod}{D})$, every prime p appearing in the sum on the left is congruent to rD modulo D. Using (2.5), we have
for each prime p in the sum, whence
 \begin{equation*}
\left\| \frac{{\alpha} h(p)}{{\lambda}(D)} \right\|
\leqslant \left|\frac{h(p)}
{qm {\lambda}(D)}\right| \| q m {\alpha} \|
\ll_h \frac{(P/L^2)^d}{q {\lambda}(D)}
\frac{q L^d {\lambda}(D)}{P^d}
= L^{-d}
= (\rho/C)^{d}.
\end{equation*}
\begin{equation*}
\left\| \frac{{\alpha} h(p)}{{\lambda}(D)} \right\|
\leqslant \left|\frac{h(p)}
{qm {\lambda}(D)}\right| \| q m {\alpha} \|
\ll_h \frac{(P/L^2)^d}{q {\lambda}(D)}
\frac{q L^d {\lambda}(D)}{P^d}
= L^{-d}
= (\rho/C)^{d}.
\end{equation*} Taking C sufficiently large, we deduce that ![]() $p \in \mathcal B$. We conclude that
$p \in \mathcal B$. We conclude that
 \begin{equation*}
\sum_{p\in\mathcal B}\log p \geqslant
\sum_{\substack{p \leqslant P/L^2
\\ p \equiv r_{qmD}
\;(\operatorname{mod}{qmD})}} \log p
\gg_{h,\varepsilon} \frac{P}{L^{d+3+\varepsilon} \varphi(D)} \gg_h \frac{\rho^{d+3+\varepsilon}P}{\varphi(D)},
\end{equation*}
\begin{equation*}
\sum_{p\in\mathcal B}\log p \geqslant
\sum_{\substack{p \leqslant P/L^2
\\ p \equiv r_{qmD}
\;(\operatorname{mod}{qmD})}} \log p
\gg_{h,\varepsilon} \frac{P}{L^{d+3+\varepsilon} \varphi(D)} \gg_h \frac{\rho^{d+3+\varepsilon}P}{\varphi(D)},
\end{equation*}as required.
Now suppose ![]() $K\geqslant 2$ and assume the induction hypothesis that theorem 9.2 holds with K − 1 in place of K. Write
$K\geqslant 2$ and assume the induction hypothesis that theorem 9.2 holds with K − 1 in place of K. Write ![]() $\mathbf{m}=(\mathbf{m}',m_K)$ and
$\mathbf{m}=(\mathbf{m}',m_K)$ and ![]() $\boldsymbol{\alpha}=(\boldsymbol{\alpha}',\alpha_K)$. The induction hypothesis, applied to
$\boldsymbol{\alpha}=(\boldsymbol{\alpha}',\alpha_K)$. The induction hypothesis, applied to
 \begin{equation*}
\frac{{\lambda}(q m_K)}{m_K} \boldsymbol{{\alpha}}',
\end{equation*}
\begin{equation*}
\frac{{\lambda}(q m_K)}{m_K} \boldsymbol{{\alpha}}',
\end{equation*}informs us that the set
 \begin{equation*}
\mathcal A = \left \{
p \leqslant P/L^2: p \equiv r_{qm_K D} \;(\operatorname{mod}{qm_K D}), \;
\left \|
\frac{h(p)}{m_K {\lambda}(D)} \boldsymbol{{\alpha}}'
\right \| \lt \frac{\rho^2}{2K^2} \right \}
\end{equation*}
\begin{equation*}
\mathcal A = \left \{
p \leqslant P/L^2: p \equiv r_{qm_K D} \;(\operatorname{mod}{qm_K D}), \;
\left \|
\frac{h(p)}{m_K {\lambda}(D)} \boldsymbol{{\alpha}}'
\right \| \lt \frac{\rho^2}{2K^2} \right \}
\end{equation*}satisfies
 \begin{align*}
\sum_{p\in\mathcal A}\log p &\geqslant \frac{P}{L^2\varphi(qm_K D)}
\Delta
\left(h,K-1; \frac{\rho^2}{2K^2}\right) \\
&\gg_{h,K,\varepsilon}
\frac{P}{\varphi(D)}
\rho^{3 + K(d+\varepsilon)} \Delta
\left(h,K-1; \frac{\rho^2}{2K^2}\right).
\end{align*}
\begin{align*}
\sum_{p\in\mathcal A}\log p &\geqslant \frac{P}{L^2\varphi(qm_K D)}
\Delta
\left(h,K-1; \frac{\rho^2}{2K^2}\right) \\
&\gg_{h,K,\varepsilon}
\frac{P}{\varphi(D)}
\rho^{3 + K(d+\varepsilon)} \Delta
\left(h,K-1; \frac{\rho^2}{2K^2}\right).
\end{align*} Let ![]() $a\in\mathbb{Z}$ be such that
$a\in\mathbb{Z}$ be such that
For each ![]() $p\in\mathcal A$, we have
$p\in\mathcal A$, we have ![]() $h(p) \ll_h (P/L^2)^d$ so, by (9.6),
$h(p) \ll_h (P/L^2)^d$ so, by (9.6),
 \begin{equation*}
\left| {\alpha}_K \frac{h(p)}{{\lambda}(D)} - \frac{a/q - \mathbf{m}' \cdot \boldsymbol{{\alpha}}'}{m_K} \frac{h(p)}{{\lambda}(D)}
\right| = \left\lvert \frac{h(p)}{m_K\lambda(D)}\right\rvert\cdot \lvert\mathbf{m}\cdot\boldsymbol{\alpha} - a/q\rvert
\ll_h L^{-d}.
\end{equation*}
\begin{equation*}
\left| {\alpha}_K \frac{h(p)}{{\lambda}(D)} - \frac{a/q - \mathbf{m}' \cdot \boldsymbol{{\alpha}}'}{m_K} \frac{h(p)}{{\lambda}(D)}
\right| = \left\lvert \frac{h(p)}{m_K\lambda(D)}\right\rvert\cdot \lvert\mathbf{m}\cdot\boldsymbol{\alpha} - a/q\rvert
\ll_h L^{-d}.
\end{equation*} As in the previous case, we have ![]() $qm_K\lambda(D) \mid h(p)$, whence
$qm_K\lambda(D) \mid h(p)$, whence
 \begin{equation*}
\left\lVert \frac{a/q - \mathbf{m}' \cdot \boldsymbol{{\alpha}}'}{m_K} \frac{h(p)}{{\lambda}(D)}\right\rVert = \left\lVert \frac{h(p)\mathbf{m}' \cdot \boldsymbol{{\alpha}}'}{m_K{\lambda}(D)}\right\rVert \lt \frac{\rho}{2}.
\end{equation*}
\begin{equation*}
\left\lVert \frac{a/q - \mathbf{m}' \cdot \boldsymbol{{\alpha}}'}{m_K} \frac{h(p)}{{\lambda}(D)}\right\rVert = \left\lVert \frac{h(p)\mathbf{m}' \cdot \boldsymbol{{\alpha}}'}{m_K{\lambda}(D)}\right\rVert \lt \frac{\rho}{2}.
\end{equation*}Thus, by the triangle inequality,
 \begin{equation*}
\left \|
{\alpha}_K \frac{h(p)}{{\lambda}(D)}
\right \| \lt \frac{\rho}2 +
O_h(L^{-d}) =
\frac{\rho}2 + O_h((C\rho^{-K})^{-d}).
\end{equation*}
\begin{equation*}
\left \|
{\alpha}_K \frac{h(p)}{{\lambda}(D)}
\right \| \lt \frac{\rho}2 +
O_h(L^{-d}) =
\frac{\rho}2 + O_h((C\rho^{-K})^{-d}).
\end{equation*} By taking C sufficiently large, we find that ![]() $p\in\mathcal B$. Therefore
$p\in\mathcal B$. Therefore
 \begin{equation*}
\sum_{p\in\mathcal B}\log p \geqslant \sum_{p\in\mathcal A}\log p \gg_{h,K,\varepsilon} \frac{P}{\varphi(D)}
\rho^{3 + K(d+\varepsilon)}
\Delta
\left(h,K-1; \frac{\rho^2}{2K^2}\right),
\end{equation*}
\begin{equation*}
\sum_{p\in\mathcal B}\log p \geqslant \sum_{p\in\mathcal A}\log p \gg_{h,K,\varepsilon} \frac{P}{\varphi(D)}
\rho^{3 + K(d+\varepsilon)}
\Delta
\left(h,K-1; \frac{\rho^2}{2K^2}\right),
\end{equation*}as required.
Acknowledgements
J.C. is supported by the Heilbronn Institute for Mathematical Research. S.C. thanks the University of Bristol for their kind hospitality on various occasions when this work was being discussed. We are grateful to the anonymous referee for their thorough report and numerous constructive comments.