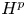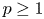Li et al. [A spectral radius type formula for approximation numbers of composition operators, J. Funct. Anal. 267(12) (2014), 4753-4774] proved a spectral radius type formula for the approximation numbers of composition operators on analytic Hilbert spaces with radial weights and on $H^{p}$ spaces, $p\geq 1$, involving Green capacity. We prove that their formula holds for a wide class of Banach spaces of analytic functions and weights.

The Hardy operator $T_a$ on a tree $\Gamma$ is defined by \[ (T_af)(x):=v(x) \int^x_a f(t)u(t)\,dt \quad \mbox{for } a, x\in \Gamma. \] Properties of $T_a$ as a map from $L^p(\Gamma)$ into itself are established for $1\le p \le \infty$. The main result is that, with appropriate assumptions on $u$ and $v$, the approximation numbers $a_n(T_a)$ of $T_a$ satisfy \begin{equation*} \tag{$*$} \lim_{n\rightarrow \infty} na_n(T_a) = \alpha_p\int_{\Gamma}|uv|\,dt \end{equation*} for a specified constant $\alpha_p$ and $1 p<\infty$. This extends results of Naimark, Newman and Solomyak for $p=2$. Hitherto, for $p\neq 2$, $(*)$ was unknown even when $\Gamma$ is an interval. Also, upper and lower estimates for the $l^q$ and weak-$l^q$ norms of $\{a_n(T_a)\}$ are determined.

2000 Mathematical Subject Classification: 47G10, 47B10.