We establish a theoretical framework for predicting friction and heat transfer coefficients in variable-property forced air convection. Drawing from concepts in high-speed wall turbulence, which also involves significant temperature, viscosity and density variations, we utilize the mean momentum balance and mean thermal balance equations to develop integral transformations that account for the impact of variable fluid properties. These transformations are then applied inversely to predict the friction and heat transfer coefficients, leveraging the universality of passive scalars transport theory. Our proposed approach is validated using a comprehensive dataset from direct numerical simulations (DNS), covering both heating and cooling conditions up to a friction Reynolds number $\textit {Re}_\tau \approx 3200$. The predicted friction and heat transfer coefficients closely match the DNS data with accuracy margin 1–2 %, representing a significant improvement over the current state of the art.

We provide scaling relations for the Nusselt number 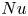$Nu$ and the friction coefficient 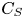$C_{S}$ in sheared Rayleigh–Bénard convection, i.e. in Rayleigh–Bénard flow with Couette- or Poiseuille-type shear forcing, by extending the Grossmann & Lohse (J. Fluid Mech., vol. 407, 2000, pp. 27–56, Phys. Rev. Lett., vol. 86, 2001, pp. 3316–3319, Phys. Rev. E, vol. 66, 2002, 016305, Phys. Fluids, vol. 16, 2004, pp. 4462–4472) theory to sheared thermal convection. The control parameters for these systems are the Rayleigh number 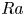$Ra$, the Prandtl number 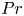$Pr$ and the Reynolds number 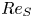$Re_S$ that characterises the strength of the imposed shear. By direct numerical simulations and theoretical considerations, we show that, in turbulent Rayleigh–Bénard convection, the friction coefficients associated with the applied shear and the shear generated by the large-scale convection rolls are both well described by Prandtl's (Ergeb. Aerodyn. Vers. Gött., vol. 4, 1932, pp. 18–29) logarithmic friction law, suggesting some kind of universality between purely shear-driven flows and thermal convection. These scaling relations hold well for 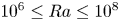$10^6 \leq Ra \leq 10^8$, 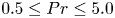$0.5 \leq Pr \leq 5.0$, and 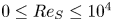$0 \leq Re_S \leq 10^4$.

We employ direct numerical simulations to investigate the heat transfer and flow structures in turbulent Rayleigh–Bénard convection in both cylindrical cells and laterally periodic domains, spanning an unprecedentedly wide range of aspect ratios $0.075 \leqslant \varGamma \leqslant 32$. We focus on Prandtl number ${Pr}=1$ and Rayleigh numbers ${{Ra}}=2\times 10^7$ and ${{Ra}}=10^8$. In both cases, with increasing aspect ratio, the heat transfer first increases, then reaches a maximum (which is more pronounced for the cylindrical case due to confinement effects), and then slightly goes down again before it finally saturates at the large aspect ratio limit, which is achieved already at $\varGamma \approx 4$. Already for $\varGamma \gtrsim 0.75$, the heat transfers in both cylindrical and laterally periodic domains become identical. The large-$\varGamma$ limit for the volume-integrated Reynolds number and the boundary layer thicknesses are also reached at $\varGamma \approx 4$. However, while the integral flow properties converge at $\varGamma \approx 4$, the confinement of a cylindrical domain impacts the temperature and velocity variance distributions up to $\varGamma \approx 16$, as thermal superstructures cannot form close to the sidewall.

The seminal Bolgiano–Obukhov (BO) theory established the fundamental framework for turbulent mixing and energy transfer in stably stratified fluids. However, the presence of BO scalings remains debatable despite their being observed in stably stratified atmospheric layers and convective turbulence. In this study, we performed precise temperature measurements with 51 high-resolution loggers above the seafloor for 46 h on the continental shelf of the northern South China Sea. The temperature observation exhibits three layers with increasing distance from the seafloor: the bottom mixed layer (BML), the mixing zone and the internal wave zone. A BO-like scaling $\alpha =-1.34\pm 0.10$ is observed in the temperature spectrum when the BML is in a weakly stable stratified ($N\sim 0.0018$ rad s$^{-1}$) and strongly sheared ($Ri\sim 0.0027$) condition, whereas in the unstably stratified convective turbulence of the BML, the scaling $\alpha =-1.76\pm 0.10$ clearly deviated from the BO theory but approached the classical $-$5/3 scaling in isotropic turbulence. This suggests that the convective turbulence is not the promise of BO scaling. In the mixing zone, where internal waves alternately interact with the BML, the scaling follows the Kolmogorov scaling. In the internal wave zone, the scaling $\alpha =-2.12 \pm 0.15$ is observed in the turbulence range and possible mechanisms are provided.

Radial unstable stratification is a potential source of turbulence in the cold regions of accretion disks. To investigate this thermal effect, here we focus on two-dimensional Rayleigh–Bénard convection in an annulus subject to radially dependent gravitational acceleration $g \propto 1/r$. Next to the Rayleigh number $Ra$ and Prandtl number $Pr$, the radius ratio $\eta$, defined as the ratio of inner and outer cylinder radii, is a crucial parameter governing the flow dynamics. Using direct numerical simulations for $Pr=1$ and $Ra$ in the range from $10^7$ to $10^{10}$, we explore how variations in $\eta$ influence the asymmetry in the flow field, particularly in the boundary layers. Our results show that in the studied parameter range, the flow is dominated by convective rolls and that the thermal boundary-layer (TBL) thickness ratio between the inner and outer boundaries varies as $\eta ^{1/2}$. This scaling is attributed to the equality of velocity scales in the inner ($u_i$) and outer ($u_o$) regions. We further derive that the temperature drops in the inner and outer TBLs scale as $1/(1+\eta ^{1/2})$ and $\eta ^{1/2}/(1+\eta ^{1/2})$, respectively. The scalings and the temperature drops are in perfect agreement with the numerical data.

Geothermal gradients and heterogeneous permeability are commonly observed in natural geological formations for underground CO$_2$ sequestration. In this study, we conduct three-dimensional direct numerical simulations on the double-diffusive convection with both unstable temperature and concentration gradients in homogeneous and heterogeneous porous media. For homogeneous porous media, the root-mean-squared velocity increases linearly with density ratio defined as the buoyancy ratio by temperature and concentration differences. The flow structures show no remarkable changes when temperature Rayleigh number ${Ra}_T$ is less than its critical value, but alter from sheet-like to cellular structures as ${Ra}_T$ surpasses this threshold. The concentration wavenumber scales approximately as $k_{rS}\sim {Ra}_e^{0.47}$ with a defined effective Rayleigh number ${Ra}_e$. By using a scale analysis, the concentration flux exhibits a consistent linear relation with the total driving forces for all simulations. For heterogeneous porous media, where the Dykstra–Parsons coefficient $V_{DP}$ and correlation length $l_{r}$ determine the spatial distribution of the permeability field, the flow is strengthened in places with higher permeability. The velocity and concentration flux are less affected by $l_{r}$ than that by $V_{DP}$. For small correlation length, the flow structures coarsen and their characteristic width generally increases with increasing heterogeneity. For large correlation length, small structures emerge in the regions with large permeability, which can be attributed to the intensified local Rayleigh number triggering more vigorous convection there. The variations of concentration flux with $l_{r}$ and $V_{DP}$ can be explained by the portion of area covered by high concentration with large vertical velocity near the boundaries.

Turbulent convection in the interiors of the Sun and the Earth occurs at high Rayleigh numbers $Ra$, low Prandtl numbers $Pr$, and different levels of rotation rates. To understand the combined effects better, we study rotating turbulent convection for $Pr = 0.021$ (for which some laboratory data corresponding to liquid metals are available), and varying Rossby numbers $Ro$, using direct numerical simulations in a slender cylinder of aspect ratio 0.1; this confinement allows us to attain high enough Rayleigh numbers. We are motivated by the earlier finding in the absence of rotation that heat transport at high enough $Ra$ is similar between confined and extended domains. We make comparisons with higher aspect ratio data where possible. We study the effects of rotation on the global transport of heat and momentum as well as flow structures (a) for increasing rotation at a few fixed values of $Ra$, and (b) for increasing $Ra$ (up to $10^{10}$) at the fixed, low Ekman number $1.45 \times 10^{-6}$. We compare the results with those from unity $Pr$ simulations for the same range of $Ra$ and $Ro$, and with the non-rotating case over the same range of $Ra$ and low $Pr$. We find that the effects of rotation diminish with increasing $Ra$. These results and comparison studies suggest that for high enough $Ra$, rotation alters convective flows in a similar manner for small and large aspect ratios, so useful insights on the effects of high thermal forcing on convection can be obtained by considering slender domains.

We studied the transport and deposition behaviour of point particles in Rayleigh–Bénard convection cells subjected to Couette-type wall shear. Direct numerical simulations (DNSs) are performed for Rayleigh number ($Ra$) in the range $10^{7} \leq Ra \leq ~10^9$ with a fixed Prandtl number $Pr = 0.71$, while the wall-shear Reynolds number ($Re_w$) is in the range $0 \leq Re_w \leq ~12\,000$. With the increase of $Re_w$, the large-scale rolls expanded horizontally, evolving into zonal flow in two-dimensional simulations or streamwise-oriented rolls in three-dimensional simulations. We observed that, for particles with a small Stokes number ($St$), they either circulated within the large-scale rolls when buoyancy dominated or drifted near the walls when shear dominated. For medium $St$ particles, pronounced spatial inhomogeneity and preferential concentration were observed regardless of the prevailing flow state. For large $St$ particles, the turbulent flow structure had a minor influence on the particles’ motion; although clustering still occurred, wall shear had a negligible influence compared with that for medium $St$ particles. We then presented the settling curves to quantify the particle deposition ratio on the walls. Our DNS results aligned well with previous theoretical predictions, which state that small $St$ particles settle with an exponential deposition ratio and large $St$ particles settle with a linear deposition ratio. For medium $St$ particles, where complex particle–turbulence interaction emerges, we developed a new model describing the settling process with an initial linear stage followed by a nonlinear stage. Unknown parameters in our model can be determined either by fitting the settling curves or using empirical relations. Compared with DNS results, our model also accurately predicts the average residence time across a wide range of $St$ for various $Re_w$.

We discuss the applicability of quasilinear-type approximations for a turbulent system with a large range of spatial and temporal scales. We consider a paradigm fluid system of rotating convection with vertical and horizontal temperature gradients. In particular, the interaction of rotation with the horizontal temperature gradient drives a ‘thermal wind’ shear flow whose strength is controlled by the horizontal temperature gradient. Varying this parameter therefore systematically alters the ordering of the shearing time scale, the convective time scale and the correlation time scale. We demonstrate that quasilinear-type approximations work well when the shearing time scale or the correlation time scale is sufficiently short. In all cases, the generalised quasilinear approximation systematically outperforms the quasilinear approximation. We discuss the consequences for statistical theories of turbulence interacting with mean gradients.

Turbulent shear flows driven by a combination of a pressure gradient and buoyancy forcing are investigated using direct numerical simulations. Specifically, we consider the set-up of a differentially heated vertical channel subject to a Poiseuille-like horizontal pressure gradient. We explore the response of the system to its three control parameters: the Grashof number $Gr$, the Prandtl number $Pr$, and the Reynolds number $Re$ of the pressure-driven flow. From these input parameters, the relative strength of buoyancy driving to the pressure gradient can be quantified by the Richardson number $Ri=Gr/Re^2$. We compare the response of the mixed vertical convection configuration to that of mixed Rayleigh–Bénard convection, and find a nearly identical behaviour, including an increase in wall friction at higher $Gr$, and a drop in the heat flux relative to natural convection for $Ri=O(1)$. This closely matched response is despite vastly different flow structures in the systems. No large-scale organisation is visible in visualisations of mixed vertical convection – an observation that is confirmed quantitatively by spectral analysis. This analysis, combined with a statistical description of the wall heat flux, highlights how moderate shear suppresses the growth of small-scale plumes and reduces the likelihood of extreme events in the local wall heat flux. Vice versa, starting from a pure shear flow, the addition of thermal driving enhances the drag due to the emission of thermal plumes.

We study the effects of Prandtl number $\mathit {Pr}$ and Rayleigh number $\mathit {Ra}$ in two-dimensional Rayleigh–Bénard convection without boundaries, i.e. with periodic boundary conditions. For Prandtl numbers in the range $10^{-3} \leqslant \mathit {Pr} \leqslant 10^2$, the viscous dissipation scales as $\epsilon _\nu \propto \mathit {Pr}^{1/2}\mathit {Ra}^{-1/4}$, which is based on the observation that enstrophy $\langle {\omega ^2}\rangle \propto \mathit {Pr}^0 \mathit {Ra}^{1/4}$, and the Nusselt number tends to follow the ‘ultimate’ scaling $\mathit {Nu} \propto \mathit {Pr}^{1/2}\mathit {Ra}^{1/2}$ for all values of $\mathit {Pr}$ considered. The inverse cascade of kinetic energy forms the power-law spectrum $\hat {E}_u(k) \propto k^{-2.3}$, which is close to $k^{-11/5}$ proposed by the Bolgiano–Obukhov (BO) scaling. The potential energy flux is not constant, in contrast to one of the main assumptions underlying the BO phenomenology. So, the direct cascade of potential energy forms the power-law spectrum $\hat {E}_\theta (k) \propto k^{-1.2}$, which deviates from the expected $k^{-7/5}$. Finally, at $\mathit {Pr} \to 0$ and $\infty$, we find that the dynamics is dominated by vertically oriented elevator modes that grow without bound, even at high Rayleigh numbers and with large-scale dissipation present.

We consider the two-dimensional Rayleigh–Bénard convection problem between Navier-slip fixed-temperature boundary conditions, and present a new upper bound for the Nusselt number (${\textit {Nu}}$). The result, based on a localization principle for the Nusselt number and an interpolation bound, exploits the regularity of the flow. On one hand our method yields a shorter proof of the celebrated result of Whitehead & Doering (Phys. Rev. Lett., vol. 106, 2011, 244501) in the case of free-slip boundary conditions. On the other hand, its combination with a new, refined estimate for the pressure gives a substantial improvement of the interpolation bounds in Drivas et al. (Phil. Trans. R. Soc. A, vol. 380, issue 2225, 2022, 20210025) for slippery boundaries. A rich description of the scaling behaviour arises from our result: depending on the magnitude of the Prandtl number (${\textit {Pr}}$) and slip length, our upper bounds indicate five possible scaling laws (where ${\textit {Ra}}$ is the Rayleigh number): ${\textit {Nu}}\sim (L_s^{-1}\,{\textit {Ra}})^{{1}/{3}}$, ${\textit {Nu}}\sim (L_s^{-2/5}\,{\textit {Ra}})^{{5}/{13}}$, ${\textit {Nu}}\sim {\textit {Ra}}^{{5}/{12}}$, ${\textit {Nu}}\sim {\textit {Pr}}^{-1/6}(L_s^{-4/3}\,{\textit {Ra}})^{{1}/{2}}$ and ${\textit {Nu}}\sim {\textit {Pr}}^{-1/6}(L_s^{-1/3}\,{\textit {Ra}})^{{1}/{2}}$.

We experimentally and numerically characterize rapidly rotating radiatively driven thermal convection, beyond the sole heat transport measurements reported by Bouillaut et al. (Proc. Natl Acad. Sci., vol. 118, 2021, e2105015118). Based on a suite of direct numerical simulations (DNS) and additional processing of the experimental data collected by Bouillaut et al. (Proc. Natl Acad. Sci., vol. 118, 2021, e2105015118), we report the simultaneous validation of the scaling predictions of the ‘geostrophic turbulence’ regime – the diffusivity-free or ‘ultimate’ regime of rapidly rotating convection – for the heat transport and the temperature fluctuations. Following such cross-validation between DNS and laboratory experiments, we further process the numerical data to validate the ‘geostrophic turbulence’ scaling predictions for the flow velocity and horizontal scale. Radiatively driven convection thus appears as a versatile set-up for the laboratory observation of the diffusivity-free regimes of various convective flows of geophysical and/or astrophysical interest.

We report on an experimental study of turbulent Rayleigh–Bénard convection with asymmetric top and bottom plates. The plates are covered with pyramid-shaped roughness elements whose aspect ratios are $\lambda =1$ or $\lambda =4$. In the low-Rayleigh-number regime ($Ra<1.9\times 10^9$), the heat transport efficiencies in the asymmetric cells, characterized by the Nusselt number, are smaller than those measured in a symmetric $\lambda = 1$ cell and are greater than those for a symmetric $\lambda = 4$ cell, whereas in the high-Rayleigh-number regime ($Ra>1.9\times 10^9$), the Nusselt numbers of the asymmetric cells are, in turn, greater than those for the symmetric cell with $\lambda = 1$ and smaller than those for the symmetric cell with $\lambda = 4$. In addition, the heat transports of individual plates are studied based on the temperature drops across both halves of the cell. In the low-$Ra$ regime, the $\lambda =1$ plate shows higher heat transfer than the $\lambda =4$ plate, while for the high-$Ra$ regime, the $\lambda =4$ plate shows a higher heat transport ability. In both regimes, the individual Nusselt number of the plate with lower heat transfer is insensitive to the topology of the other plate. Besides, it is found that the symmetry of the centre temperature distribution is robust to the symmetry breaking of boundary topographies. For the $Ra$ range explored, a weak temperature inversion is observed in the bulk of asymmetric rough cells. Finally, we remark that the temperature fluctuation at the cell centre and the Reynolds number associated with the large-scale circulation show universal power laws in terms of the flux Rayleigh number as $\sigma _{T_{c}}\sim Ra_F^{0.68}$ and $Re_{LSC}\sim Ra_F^{0.36}$, respectively.

We report a numerical investigation of a previously noticed but less explored flow state transition in two-dimensional turbulent Rayleigh–Bénard convection. The simulations are performed in a square domain over a Rayleigh number range of $10^7 \leq Ra \leq 2 \times 10^{11}$ and a Prandtl number range of $0.25 \leq Pr \leq 20$. The transition is characterized by the emergence of multiple satellite eddies with increasing $Ra$, which orbit around and interact with the main vortex roll in the system. Consequently, the main roll is squeezed to a smaller size compared with the domain and wanders around in the bulk region irregularly and extensively. This is in sharp contrast to the flow state before the transition, which is featured by a domain-sized circulatory roll with its vortex centre ‘condensed’ near the domain's centre. Detailed velocity field analysis reveals that there exists an abrupt increase in the energy fluctuations of the Fourier modes during the transition. Based on this phase-transition-like signal, the critical condition for the transition is found to follow a scaling relation as $Ra_t \sim Pr^{1.41}$ where $Ra_t$ is the critical Rayleigh number for the transition. This scaling relation is quantitatively explained by a phenomenological model grounded on the bistability behaviour (i.e. spontaneous and stochastic switching between the two flow states) observed at the edge of the transition. The model can also account for the effects of aspect ratio on the transition reported in the literature (van der Poel et al., Phys. Fluids, vol. 24, 2012).

We consider an internally heated fluid between parallel plates with fixed thermal fluxes. For a large class of heat sources that vary in the direction of gravity, we prove that $\smash { \smash {{\langle {\delta T} \rangle _h}} } \geq \sigma R^{-1/3} - \mu$, where $\smash { \smash {{\langle {\delta T} \rangle _h}} }$ is the average temperature difference between the bottom and top plates, $R$ is a ‘flux’ Rayleigh number and the constants $\sigma,\mu >0$ depend on the geometric properties of the internal heating. This result implies that mean downward conduction (for which $\smash { \smash {{\langle {\delta T} \rangle _h}} }< 0$) is impossible for a range of Rayleigh numbers smaller than a critical value $R_0:=(\sigma /\mu )^{3}$. The bound demonstrates that $R_0$ depends on the heating distribution and can be made arbitrarily large by concentrating the heating near the bottom plate. However, for any given fixed heating profile of the class we consider, the corresponding value of $R_0$ is always finite. This points to a fundamental difference between internally heated convection and its limiting case of Rayleigh–Bénard convection with fixed-flux boundary conditions, for which $\smash {{\langle {\delta T} \rangle _h}}$ is known to be positive for all $R$.

We perform linear stability analysis and direct numerical simulations to study the effect of the radius ratio on the instability and flow characteristics of the sheared annular centrifugal Rayleigh–Bénard convection, where the cold inner cylinder and the hot outer cylinder rotate with a small angular velocity difference. With the shear enhancement, the thermal convection is suppressed and finally becomes stable for different radius ratios $\{\eta \in \mathbb {R}|0.2\leqslant \eta \le 0.95\}$. Considering the inhomogeneous distribution of shear stresses in the base flow, a new global Richardson number $Ri_g$ is defined and the marginal-state curves for different radius ratios are successfully unified in the parameter domain of $Ri_g$ and the Rayleigh number $Ra$. The results are consistent with the marginal-state curve of the wall-sheared classical Rayleigh–Bénard convection in the streamwise direction, demonstrating that the basic stabilization mechanisms are identical. Moreover, systems with small radius ratios exhibit greater geometric asymmetry. On the one hand, this results in a smaller equivalent aspect ratio for the system, accommodating fewer convection roll pairs; fewer roll pairs are more likely to cause a transition in the flow structure during shear enhancement. On the other hand, the shear distribution is more inhomogeneous, allowing for an outward shift of the convection region and the elevation of bulk temperature under strong shear.

This study proposes a new mechanism that can lead to layering or convection from the finite amplitude perturbation acting on the double diffusive convection with uniform background shear. We focus on the double diffusive convection in the diffusive regime with the cold fresh water laying above the warm salty water. We demonstrate that, although the unperturbed system is linearly stable, the finite amplitude perturbation can trigger the initial flow motions which subsequently obtain energy from the gravitational potential energy and from the uniform background shear, and evolve to layering or convection. By using the linear stability analysis for the initial growth stage and the energy analysis for the following transitional stage, the critical Richardson number can be predicted theoretically. Here the Richardson number measures the relative strength of stratification to the background shear. The dominant wavenumbers and the growth rates of the corresponding modes given by linear theory agree well with the two-dimensional direct numerical simulations, and so does the critical Richardson number predicted by the theoretical model. The layering state is dominated by the double diffusion process, while the convection state at smaller Richardson number exhibits stronger influences from shear and generates smaller heat and salinity fluxes. The theoretical model is further applied to the parameter range which is relevant to the real oceanic environments and reveals that for the typical density ratio observed in the staircase regions in the Arctic Ocean, the current mechanism can lead to layering for relatively weak shear.

We present a systematic study on the effects of small aspect ratios $\varGamma$ on heat transport in liquid metal convection with a Prandtl number of $Pr=0.029$. The study covers $1/20\le \varGamma \le 1$ experimentally and $1/50\le \varGamma \le 1$ numerically, and a Rayleigh number $Ra$ range of $4\times 10^3 \le Ra \le 7\times 10^{9}$. It is found experimentally that the local effective heat transport scaling exponent $\gamma$ changes with both $Ra$ and $\varGamma$, attaining a $\varGamma$-dependent maximum value before transition-to-turbulence and approaches $\gamma =0.25$ in the turbulence state as $Ra$ increases. Just above the onset of convection, Shishkina (Phys. Rev. Fluids, vol 6, 2021, 090502) derived a length scale $\ell =H/(1+1.49\varGamma ^{-2})^{1/3}$. Our numerical study shows $Ra_{\ell }$, i.e. $Ra$ based on $\ell$, serves as a proper control parameter for heat transport above the onset with $Nu-1=0.018(1+0.34/\varGamma ^2)(Ra/Ra_{c,\varGamma }-1)$. Here $Ra_{c,\varGamma }$ represents the $\varGamma$-dependent critical $Ra$ for the onset of convection and $Nu$ is the Nusselt number. In the turbulent state, for a general scaling law of $Nu-1\sim Ra^\alpha$, we propose a length scale $\ell = H/(1+1.49\varGamma ^{-2})^{1/[3(1-\alpha )]}$. In the case of turbulent liquid metal convection with $\alpha =1/4$, our measurement shows that the heat transport will become weakly dependent on $\varGamma$ with $Ra_{\ell }\equiv Ra/(1+1.49\varGamma ^{-2})^{4/3} \ge 7\times 10^5$. Finally, once the flow becomes time-dependent, the growth rate of $Nu$ with $Ra$ declines compared with the linear growth rate in the convection state. A hysteresis is observed in a $\varGamma =1/3$ cell when the flow becomes time-dependent. Measurements of the large-scale circulation suggest the hysteresis is caused by the system switching from a single-roll-mode to a double-roll-mode in an oscillation state.

To date, a comprehensive understanding of the influence of the Prandtl number ($Pr$) on flow topology in turbulent Rayleigh–Bénard convection (RBC) remains elusive. In this study, we present an experimental investigation into the evolution of flow topology in quasi-two-dimensional turbulent RBC with $7.0 \leq Pr \leq 244.2$ and $2.03\times 10^{8} \leq Ra \leq 2.81\times 10^{9}$. Particle image velocimetry (PIV) measurements reveal the flow transitions from multiple-roll state to single-roll state with increasing $Ra$, and the transition is hindered with increasing $Pr$, i.e. the transitional Rayleigh number $Ra_t$ increases with $Pr$. We mapped out a phase diagram on the flow topology change on $Ra$ and $Pr$, and identified the scaling of $Ra_t$ on $Pr$: $Ra_t \sim Pr^{0.93}$ in the low $Pr$ range, and $Ra_t \sim Pr^{3.3}$ in the high $Pr$ range. The scaling in the low $Pr$ range is consistent with the model of balance of energy dissipation time and plume travel time that we proposed in our previous study, while the scaling in the high $Pr$ range implies a new governing mechanism. For the first time, the scaling of $Re$ on $Ra$ and $Pr$ is acquired through full-field PIV velocity measurement, $Re \sim Ra^{0.63}\,Pr^{-0.87}$. We also propose that increasing horizontal velocity promotes the formation of the large-scale circulation (LSC), especially for the high $Pr$ case. Our proposal was verified by achieving LSC through introducing horizontal driving force $Ra_H$ by tilting the convection cell with a small angle.