Let Sn,n≥1, be the successive sums of the payoffs in the classical St. Petersburg game. The celebrated Feller weak law states that Sn∕(nlog2n)→ℙ1 as n→∞. In this paper we review some earlier results of ours and extend some of them as we consider an asymmetric St. Petersburg game, in which the distribution of the payoff X is given by ℙ(X=srk-1)=pqk-1,k=1,2,…, where p+q=1 and s,r>0. Two main results are extensions of the Feller weak law and the convergence in distribution theorem of Martin-Löf (1985). Moreover, it is well known that almost-sure convergence fails, though Csörgő and Simons (1996) showed that almost-sure convergence holds for trimmed sums and also for sums trimmed by an arbitrary fixed number of maxima. In view of the discreteness of the distribution we focus on `max-trimmed sums', that is, on the sums trimmed by the random number of observations that are equal to the largest one, and prove limit theorems for simply trimmed sums, for max-trimmed sums, as well as for the `total maximum'. Analogues with respect to the random number of summands equal to the minimum are also obtained and, finally, for joint trimming.

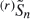 , which is obtained by deleting the
, which is obtained by deleting the 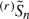 but not (completely) for
but not (completely) for 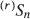 .
.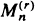 (the rth largest among a sample of
(the rth largest among a sample of 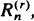 and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as
and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as 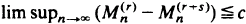 a.s. for some finite constant
a.s. for some finite constant 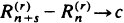 a.s. for some constant
a.s. for some constant 