1 results
SHIDLOVSKY’S MULTIPLICITY ESTIMATE AND IRRATIONALITY OF ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 145-172
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
-
In this paper we follow the approach of Bertrand–Beukers (and of Bertrand’s later work), based on differential Galois theory, to prove a very general version of Shidlovsky’s lemma that applies to Padé-approximation problems at several points, both at functional and numerical levels (that is, before and after evaluating at a specific point). This allows us to obtain a new proof of the Ball–Rivoal theorem on irrationality of infinitely many values of the Riemann zeta function at odd integers, inspired by the proof of the Siegel–Shidlovsky theorem on values of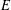
$E$-functions: Shidlovsky’s lemma is used to replace Nesterenko’s linear independence criterion with Siegel’s, so that no lower bound is needed on the linear forms in zeta values. The same strategy provides a new proof, and a refinement, of Nishimoto’s theorem on values of 
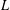$L$-functions of Dirichlet characters.
