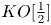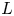1 results
The family signature theorem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 January 2023, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We discuss several versions of the Family Signature Theorem: in rational cohomology using ideas of Meyer, in $KO[\tfrac {1}{2}]$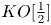
-theory using ideas of Sullivan, and finally in symmetric $L$
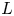-theory using ideas of Ranicki. Employing recent developments in Grothendieck–Witt theory, we give a quite complete analysis of the resulting invariants. As an application we prove that the signature is multiplicative modulo 4 for fibrations of oriented Poincaré complexes, generalizing a result of Hambleton, Korzeniewski and Ranicki, and discuss the multiplicativity of the de Rham invariant.
