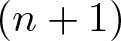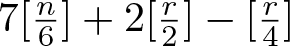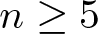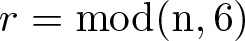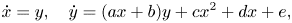In this article, we explore the bifurcation problem of limit cycles near the double eight figure loop (compound cycle with a 2-polycycle connecting two homoclinic loops). A general theory is established to find the lower bound of the maximal number of limit cycles (isolated periodic orbits) near the double eight figure loop. The Liénard system, a well-known nonlinear dynamical model, appears in a natural way in physics, chemistry, engineering, and so on, where periodic phenomena play a relevant role. As an application, we investigate an 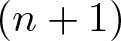$(n+1)$th-order generalized Liénard system and prove the system has at least 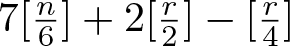$7[\frac{n}{6}]+2[\frac{r}{2}]-[\frac{r}{4}]$ limit cycles near the double eight figure loop for any 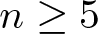$n\geq5$ and 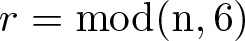$r=\rm mod(n,6)$, and their distribution is also gained.

The local structure of rotationally symmetric Finsler surfaces with vanishing flag curvature is completely determined in this paper. A geometric method for constructing such surfaces is introduced. The construction begins with a planar vector field X that depends on two functions of one variable. It is shown that the flow of X could be used to generate a generalized Finsler surface with zero flag curvature. Moreover, this generalized structure reduces to a regular Finsler metric if and only if X has an isochronous center. By relating X to a Liénard system, we obtain the isochronicity condition and discover numerous new examples of complete flat Finsler surfaces, depending on an odd function and an even function.

We classify the global phase portraits in the Poincaré disc of the quadratic polynomial Liénard differential systems

\dot{x}=y, \quad \dot{y}=(ax+b)y+cx^2+dx+e,