Let F be the gamma distribution function with parameters a > 0 and α > 0 and let Gs be the negative binomial distribution function with parameters α and a/s, s > 0. By combining both probabilistic and approximation-theoretic methods, we obtain sharp upper and lower bounds for 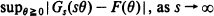 . In particular, we show that the exact order of uniform convergence is s–p, where p = min(1, α). Various kinds of applications concerning charged multiplicity distributions, the Yule birth process and Bernstein-type operators are also given.
. In particular, we show that the exact order of uniform convergence is s–p, where p = min(1, α). Various kinds of applications concerning charged multiplicity distributions, the Yule birth process and Bernstein-type operators are also given.

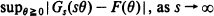 . In particular, we show that the exact order of uniform convergence is
. In particular, we show that the exact order of uniform convergence is 