We study minimizers of the Allen–Cahn system. We consider the $\varepsilon$-energy functional with Dirichlet values and we establish the $\Gamma$-limit. The minimizers of the limiting functional are closely related to minimizing partitions of the domain. Finally, utilizing that the triod and the straight line are the only minimal cones in the plane together with regularity results for minimal curves, we determine the precise structure of the minimizers of the limiting functional, and thus the limit of minimizers of the $\varepsilon$-energy functional as $\varepsilon \rightarrow 0$.

This paper develops a framework to include Dirichlet boundary conditions on a subset ofthe boundary which depends on time. In this model, the boundary conditions are weaklyenforced with the help of a Lagrange multiplier method. In order to avoid that the ansatzspace of the Lagrange multiplier depends on time, a bi-Lipschitz transformation, whichmaps a fixed interval onto the Dirichlet boundary, is introduced. An inf-sup condition aswell as existence results are presented for a class of second order initial-boundary valueproblems. For the semi-discretization in space, a finite element scheme is presented whichsatisfies a discrete stability condition. Because of the saddle point structure of theunderlying PDE, the resulting system is a DAE of index 3.

We consider a two-player zero-sum-game in a bounded open domain Ω described as follows: at a point x ∈ Ω, Players I and II play an ε-step tug-of-war game with probability α, and with probability β (α + β = 1), a random point in the ball of radius ε centered at x is chosen. Once the game position reaches the boundary, Player II pays Player I the amount given by a fixed payoff function F. We give a detailed proof of the fact that the value functions of this game satisfy the Dynamic Programming Principle

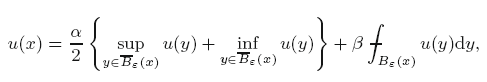
for x ∈ Ω with u(y) = F(y) when y ∉ Ω. This principle implies the existence of quasioptimal Markovian strategies.