We develop a theory of ergodicity for unbounded functions ø: J → X, where J is a subsemigroup of a locally compact abelian group G and X is a Banach space. It is assumed that ø is continuous and dominated by a weight w defined on G. In particular, we establish total ergodicity for the orbits of an (unbounded) strongly continuous representation T: G → L(X) whose dual representation has no unitary point spectrum. Under additional conditions stability of the orbits follows. To study spectra of functions, we use Beurling algebras L1w(G) and obtain new characterizations of their maximal primary ideals, when w is non-quasianalytic, and of their minimal primary ideals, when w has polynomial growth. It follows that, relative to certain translation invariant function classes 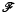 , the reduced Beurling spectrum of ø is empty if and only if ø ∈
, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 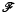 . For the zero class, this is Wiener's tauberian theorem.
. For the zero class, this is Wiener's tauberian theorem.

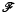 , the reduced Beurling spectrum of ø is empty if and only if ø ∈
, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 