We study the low-temperature 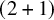 $(2+1)$D solid-on-solid model on
$(2+1)$D solid-on-solid model on 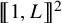 with zero boundary conditions and nonnegative heights (a floor at height
with zero boundary conditions and nonnegative heights (a floor at height 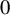 $0$). Caputo et al. (2016) established that this random surface typically admits either
$0$). Caputo et al. (2016) established that this random surface typically admits either  $\mathfrak h $ or
$\mathfrak h $ or 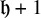 $\mathfrak h+1$ many nested macroscopic level line loops
$\mathfrak h+1$ many nested macroscopic level line loops 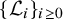 $\{\mathcal L_i\}_{i\geq 0}$ for an explicit
$\{\mathcal L_i\}_{i\geq 0}$ for an explicit 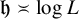 $\mathfrak h\asymp \log L$, and its top loop
$\mathfrak h\asymp \log L$, and its top loop 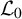 $\mathcal L_0$ has cube-root fluctuations: For example, if
$\mathcal L_0$ has cube-root fluctuations: For example, if 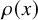 $\rho (x)$ is the vertical displacement of
$\rho (x)$ is the vertical displacement of 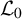 $\mathcal L_0$ from the bottom boundary point
$\mathcal L_0$ from the bottom boundary point 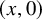 $(x,0)$, then
$(x,0)$, then 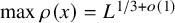 $\max \rho (x) = L^{1/3+o(1)}$ over
$\max \rho (x) = L^{1/3+o(1)}$ over 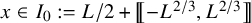 . It is believed that rescaling
. It is believed that rescaling 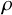 $\rho $ by
$\rho $ by 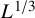 $L^{1/3}$ and
$L^{1/3}$ and 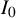 $I_0$ by
$I_0$ by 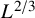 $L^{2/3}$ would yield a limit law of a diffusion on
$L^{2/3}$ would yield a limit law of a diffusion on 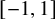 $[-1,1]$. However, no nontrivial lower bound was known on
$[-1,1]$. However, no nontrivial lower bound was known on 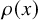 $\rho (x)$ for a fixed
$\rho (x)$ for a fixed 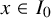 $x\in I_0$ (e.g.,
$x\in I_0$ (e.g., 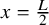 $x=\frac L2$), let alone on
$x=\frac L2$), let alone on 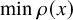 $\min \rho (x)$ in
$\min \rho (x)$ in 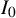 $I_0$, to complement the bound on
$I_0$, to complement the bound on 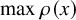 $\max \rho (x)$. Here, we show a lower bound of the predicted order
$\max \rho (x)$. Here, we show a lower bound of the predicted order 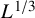 $L^{1/3}$: For every
$L^{1/3}$: For every 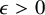 $\epsilon>0$, there exists
$\epsilon>0$, there exists 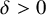 $\delta>0$ such that
$\delta>0$ such that 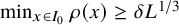 $\min _{x\in I_0} \rho (x) \geq \delta L^{1/3}$ with probability at least
$\min _{x\in I_0} \rho (x) \geq \delta L^{1/3}$ with probability at least 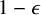 $1-\epsilon $. The proof relies on the Ornstein–Zernike machinery due to Campanino–Ioffe–Velenik and a result of Ioffe, Shlosman and Toninelli (2015) that rules out pinning in Ising polymers with modified interactions along the boundary. En route, we refine the latter result into a Brownian excursion limit law, which may be of independent interest. We further show that in a
$1-\epsilon $. The proof relies on the Ornstein–Zernike machinery due to Campanino–Ioffe–Velenik and a result of Ioffe, Shlosman and Toninelli (2015) that rules out pinning in Ising polymers with modified interactions along the boundary. En route, we refine the latter result into a Brownian excursion limit law, which may be of independent interest. We further show that in a 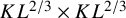 $ K L^{2/3}\times K L^{2/3}$ box with boundary conditions
$ K L^{2/3}\times K L^{2/3}$ box with boundary conditions 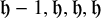 $\mathfrak h-1,\mathfrak h,\mathfrak h,\mathfrak h$ (i.e.,
$\mathfrak h-1,\mathfrak h,\mathfrak h,\mathfrak h$ (i.e., 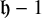 $\mathfrak h-1$ on the bottom side and
$\mathfrak h-1$ on the bottom side and 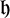 $\mathfrak h$ elsewhere), the limit of
$\mathfrak h$ elsewhere), the limit of 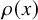 $\rho (x)$ as
$\rho (x)$ as 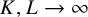 $K,L\to \infty $ is a Ferrari–Spohn diffusion.
$K,L\to \infty $ is a Ferrari–Spohn diffusion.