We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A topological space X is said to be somewhat normal provided that for each open cover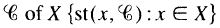 
is a normal cover of X. We show that a completely regular somewhat normal space need not be normal, thereby answering a question of W. M. Fleischman. We note that a collectionwise normal somewhat normal space need not be almost 2-fully normal, as had previously been asserted, and that neither the perfect image nor the perfect preimage of a somewhat normal space has to be somewhat normal.
A space has the shrinking property if, for every open cover {Va | a ∈ A}, there is an open cover {Wa | a ∈ A} with 
for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.
