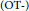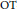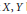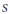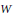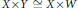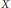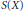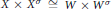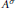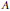2 results
The Chern–Ricci Flow on Oeljeklaus–Toma Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 220-240
- Print publication:
- 01 February 2017
-
- Article
-
- You have access
- Export citation
-
We study the Chern-Ricci flow, an evolution equation of Hermitian metrics, on a family of Oeljeklaus–Toma
$\left( \text{OT-} \right)$ manifolds that are non-Kähler compact complex manifolds with negative Kodaira dimension. We prove that after an initial conformal change, the flow converges in the Gromov–Hausdorff sense to a torus with a flat Riemannian metric determined by the 
$\text{OT}$-manifolds themselves.
Discreteness For the Set of Complex Structures On a Real Variety
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 3 / 01 September 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-322
- Print publication:
- 01 September 2003
-
- Article
-
- You have access
- Export citation
-
Let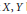
$X,\,Y$ be reduced and irreducible compact complex spaces and 
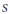$S$ the set of all isomorphism classes of reduced and irreducible compact complex spaces 
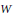$W$ such that 
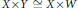$X\,\times \,Y\,\cong \,X\,\times \,W$. Here we prove that 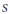$S$ is at most countable. We apply this result to show that for every reduced and irreducible compact complex space 
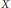$X$ the set 
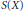$S(X)$ of all complex reduced compact complex spaces 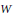$W$ with 
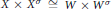$X\,\times \,{{X}^{\sigma }}\,\cong \,W\,\times \,{{W}^{\sigma }}$ (where 
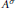${{A}^{\sigma }}$ denotes the complex conjugate of any variety 
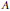$A$) is at most countable.
