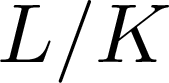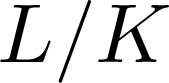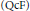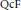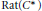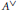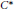We extend the group-theoretic notion of conditional flatness for a localization functor to any pointed category, and investigate it in the context of homological categories and of semi-abelian categories. In the presence of functorial fiberwise localization, analogous results to those obtained in the category of groups hold, and we provide existence theorems for certain localization functors in specific semi-abelian categories. We prove that a Birkhoff subcategory of an ideal determined category yields a conditionally flat localization, and explain how conditional flatness corresponds to the property of admissibility of an adjunction from the point of view of categorical Galois theory. Under the assumption of fiberwise localization, we give a simple criterion to determine when a (normal epi)-reflection is a torsion-free reflection. This is shown to apply, in particular, to nullification functors in any semi-abelian variety of universal algebras. We also relate semi-left-exactness for a localization functor L with what is called right properness for the L-local model structure.

The Hopf–Galois structures admitted by a Galois extension of fields $ L/K $ with Galois group G correspond bijectively with certain subgroups of $ \mathrm{Perm}(G) $. We use a natural partition of the set of such subgroups to obtain a method for partitioning the set of corresponding Hopf–Galois structures, which we term ρ-conjugation. We study properties of this construction, with particular emphasis on the Hopf–Galois analogue of the Galois correspondence, the connection with skew left braces, and applications to questions of integral module structure in extensions of local or global fields. In particular, we show that the number of distinct ρ-conjugates of a given Hopf–Galois structure is determined by the corresponding skew left brace, and that if $ H, H^{\prime} $ are Hopf algebras giving ρ-conjugate Hopf–Galois structures on a Galois extension of local or global fields $ L/K $ then an ambiguous ideal $ \mathfrak{B} $ of L is free over its associated order in H if and only if it is free over its associated order in Hʹ. We exhibit a variety of examples arising from interactions with existing constructions in the literature.

We show that the isomorphism problems for left distributive algebras, racks, quandles and kei are as complex as possible in the sense of Borel reducibility. These algebraic structures are important for their connections with the theory of knots, links and braids. In particular, Joyce showed that a quandle can be associated with any knot, and this serves as a complete invariant for tame knots. However, such a classification of tame knots heuristically seemed to be unsatisfactory, due to the apparent difficulty of the quandle isomorphism problem. Our result confirms this view, showing that, from a set-theoretic perspective, classifying tame knots by quandles replaces one problem with (a special case of) a much harder problem.

In this paper, we introduce the notion of the equivalence relation, called n-isoclinism, between crossed modules of groups, and give some basic properties of this notion. In particular, we obtain some criteria under which crossed modules are n-isoclinic. Also, we present the notion of n-stem crossed module and, under some conditions, determine them within an n-isoclinism class.

“Co-Frobenius” coalgebras were introduced as dualizations of Frobenius algebras. We previously showed that they admit left-right symmetric characterizations analogous to those of Frobenius algebras. We consider the more general quasi-co-Frobenius 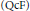$\left( \text{QcF} \right)$ coalgebras. The first main result in this paper is that these also admit symmetric characterizations: a coalgebra is 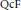$\text{QcF}$ if it is weakly isomorphic to its (left, or right) rational dual 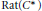$\text{Rat}\left( {{C}^{*}} \right)$ in the sense that certain coproduct or product powers of these objects are isomorphic. Fundamental results of Hopf algebras, such as the equivalent characterizations of Hopf algebras with nonzero integrals as left (or right) co-Frobenius, 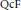$\text{QcF}$, semiperfect or with nonzero rational dual, as well as the uniqueness of integrals and a short proof of the bijectivity of the antipode for such Hopf algebras all follow as a consequence of these results. This gives a purely representation theoretic approach to many of the basic fundamental results in the theory of Hopf algebras. Furthermore, we introduce a general concept of Frobenius algebra, which makes sense for infinite dimensional and for topological algebras, and specializes to the classical notion in the finite case. This will be a topological algebra $A$ that is isomorphic to its complete topological dual 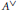${{A}^{\vee }}$. We show that $A$ is a (quasi)Frobenius algebra if and only if $A$ is the dual 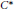${{C}^{*}}$ of a (quasi)co-Frobenius coalgebra $C$. We give many examples of co-Frobenius coalgebras and Hopf algebras connected to category theory, homological algebra and the newer $q$-homological algebra, topology or graph theory, showing the importance of the concept.