It is shown that every model of NF admits a permutation model containing an internal automorphism.

After discussing the limitations inherent to all set-theoretic reflection principles akin to those studied by A. Lévy et. al. in the 1960s, we introduce new principles of reflection based on the general notion of Structural Reflection and argue that they are in strong agreement with the conception of reflection implicit in Cantor’s original idea of the unknowability of the Absolute, which was subsequently developed in the works of Ackermann, Lévy, Gödel, Reinhardt, and others. We then present a comprehensive survey of results showing that different forms of the new principle of Structural Reflection are equivalent to well-known large cardinal axioms covering all regions of the large-cardinal hierarchy, thereby justifying the naturalness of the latter.

We prove two general results about the preservation of extendible and $C^{(n)}$ -extendible cardinals under a wide class of forcing iterations (Theorems 5.4 and 7.5). As applications we give new proofs of the preservation of Vopěnka’s Principle and $C^{(n)}$ -extendible cardinals under Jensen’s iteration for forcing the GCH [17], previously obtained in [8, 27], respectively. We prove that $C^{(n)}$ -extendible cardinals are preserved by forcing with standard Easton-support iterations for any possible $\Delta _2$ -definable behaviour of the power-set function on regular cardinals. We show that one can force proper class-many disagreements between the universe and HOD with respect to the calculation of successors of regular cardinals, while preserving $C^{(n)}$ -extendible cardinals. We also show, assuming the GCH, that the class forcing iteration of Cummings–Foreman–Magidor for forcing $\diamondsuit _{\kappa ^+}^+$ at every $\kappa $ [10] preserves $C^{(n)}$ -extendible cardinals. We give an optimal result on the consistency of weak square principles and $C^{(n)}$ -extendible cardinals. In the last section prove another preservation result for $C^{(n)}$ -extendible cardinals under very general (not necessarily definable or weakly homogeneous) class forcing iterations. As applications we prove the consistency of $C^{(n)}$ -extendible cardinals with $\mathrm {{V}}=\mathrm {{HOD}}$ , and also with $\mathrm {GA}$ (the Ground Axiom) plus $\mathrm {V}\neq \mathrm {HOD}$ , the latter being a strengthening of a result from [14].

The dissertation under comment is a contribution to the area of Set Theory concerned with the interactions between the method of Forcing and the so-called Large Cardinal axioms.

The dissertation is divided into two thematic blocks. In Block I we analyze the large-cardinal hierarchy between the first supercompact cardinal and Vopěnka’s Principle (Part I). In turn, Block II is devoted to the investigation of some problems arising from Singular Cardinal Combinatorics (Part II and Part III).

We commence Part I by investigating the Identity Crisis phenomenon in the region comprised between the first supercompact cardinal and Vopěnka’s Principle. As a result, we generalize Magidor’s classical theorems [2] to this higher region of the large-cardinal hierarchy. Also, our analysis allows to settle all the questions that were left open in [1]. Finally, we conclude Part I by presenting a general theory of preservation of 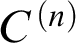$C^{(n)}$ -extendible cardinals under class forcing iterations. From this analysis we derive several applications. For instance, our arguments are used to show that an extendible cardinal is consistent with “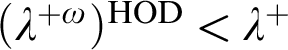 $(\lambda ^{+\omega })^{\mathrm {HOD}}<\lambda ^+$ , for every regular cardinal $\lambda $ .” In particular, if Woodin’s HOD Conjecture holds, and therefore it is provable in ZFC + “There exists an extendible cardinal” that above the first extendible cardinal every singular cardinal $\lambda $ is singular in HOD and $(\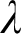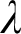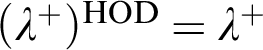lambda ^+)^{\textrm {{HOD}}}=\lambda ^+$ , there may still be no agreement at all between V and HOD about successors of regular cardinals.

In Part II and Part III we analyse the relationship between the Singular Cardinal Hypothesis (SCH) with other relevant combinatorial principles at the level of successors of singular cardinals. Two of these are the Tree Property and the Reflection of Stationary sets, which are central in Infinite Combinatorics.

Specifically, Part II is devoted to prove the consistency of the Tree Property at both 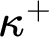$\kappa ^+$ and 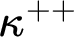$\kappa ^{++}$ , whenever 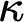$\kappa $ is a strong limit singular cardinal witnessing an arbitrary failure of the SCH. This generalizes the main result of [3] in two senses: it allows arbitrary cofinalities for 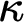$\kappa $ and arbitrary failures for the SCH.

In the last part of the dissertation (Part III) we introduce the notion of 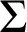$\Sigma $ -Prikry forcing. This new concept allows an abstract and uniform approach to the theory of Prikry-type forcings and encompasses several classical examples of Prikry-type forcing notions, such as the classical Prikry forcing, the Gitik-Sharon poset, or the Extender Based Prikry forcing, among many others.

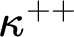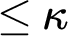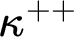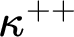Our motivation in this part of the dissertation is to prove an iteration theorem at the level of the successor of a singular cardinal. Specifically, we aim for a theorem asserting that every $\kappa ^{++}$ -length iteration with support of size $\leq \kappa $ has the $\kappa ^{++}$ -cc, provided the iterates belong to a relevant class of $\kappa ^{++}$ -cc forcings. While there are a myriad of works on this vein for regular cardinals, this contrasts with the dearth of investigations in the parallel context of singular cardinals. Our main contribution is the proof that such a result is available whenever the class of forcings under consideration is the family of $\Sigma $ -Prikry forcings. Finally, and as an application, we prove that it is consistent—modulo large cardinals—the existence of a strong limit cardinal 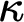$\kappa $ with countable cofinality such that 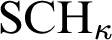$\mathrm {SCH}_\kappa $ fails and every finite family of stationary subsets of 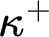$\kappa ^+$ reflects simultaneously.

In contrast to the robust mutual interpretability phenomenon in set theory, Ali Enayat proved that bi-interpretation is absent: distinct theories extending ZF are never bi-interpretable and models of ZF are bi-interpretable only when they are isomorphic. Nevertheless, for natural weaker set theories, we prove, including Zermelo–Fraenkel set theory $\mathrm {ZFC}^{-}$ without power set and Zermelo set theory Z, there are nontrivial instances of bi-interpretation. Specifically, there are well-founded models of $\mathrm {ZFC}^{-}$ that are bi-interpretable, but not isomorphic—even $\langle H_{\omega _1},\in \rangle $ and $ \langle H_{\omega _2},\in \rangle $ can be bi-interpretable—and there are distinct bi-interpretable theories extending $\mathrm {ZFC}^{-}$ . Similarly, using a construction of Mathias, we prove that every model of ZF is bi-interpretable with a model of Zermelo set theory in which the replacement axiom fails.

In this paper we study the notion of $C^{(n)}$ -supercompactness introduced by Bagaria in [3] and prove the identity crises phenomenon for such class. Specifically, we show that consistently the least supercompact is strictly below the least $C^{(1)}$ -supercompact but also that the least supercompact is $C^{(1)}$ -supercompact (and even $C^{(n)}$ -supercompact). Furthermore, we prove that under suitable hypothesis the ultimate identity crises is also possible. These results solve several questions posed by Bagaria and Tsaprounis.

We analyze the precise modal commitments of several natural varieties of set-theoretic potentialism, using tools we develop for a general model-theoretic account of potentialism, building on those of Hamkins, Leibman and Löwe [14], including the use of buttons, switches, dials and ratchets. Among the potentialist conceptions we consider are: rank potentialism (true in all larger $V_\beta $ ), Grothendieck–Zermelo potentialism (true in all larger $V_\kappa $ for inaccessible cardinals $\kappa $ ), transitive-set potentialism (true in all larger transitive sets), forcing potentialism (true in all forcing extensions), countable-transitive-model potentialism (true in all larger countable transitive models of ZFC), countable-model potentialism (true in all larger countable models of ZFC), and others. In each case, we identify lower bounds for the modal validities, which are generally either S4.2 or S4.3, and an upper bound of S5, proving in each case that these bounds are optimal. The validity of S5 in a world is a potentialist maximality principle, an interesting set-theoretic principle of its own. The results can be viewed as providing an analysis of the modal commitments of the various set-theoretic multiverse conceptions corresponding to each potentialist account.

We investigate some versions of amoeba for tree-forcings in the generalized Cantor and Baire spaces. This answers [10, Question 3.20] and generalizes a line of research that in the standard case has been studied in [11], [13], and [7]. Moreover, we also answer questions posed in [3] by Friedman, Khomskii, and Kulikov, about the relationships between regularity properties at uncountable cardinals. We show ${\bf{\Sigma }}_1^1$-counterexamples to some regularity properties related to trees without club splitting. In particular we prove a strong relationship between the Ramsey and the Baire properties, in slight contrast with the standard case.

Exploring further the properties of ITRM-recognizable reals started in [1], we provide a detailed analysis of recognizable reals and their distribution in Gödels constructible universe L. In particular, we show that new unrecognizable reals are generated at every index $\gamma \, \ge \,\omega _\omega ^{CK}$. We give a machine-independent characterization of recognizability by proving that a real r is recognizable if and only if it is ${\Sigma _1}$-definable over ${L_{\omega _\omega ^{CK,\,r}}}$ and that $r\, \in \,{L_{\omega _\omega ^{CK,\,r}}}$ for every recognizable real r and show that either every or no r with $r\, \in \,{L_{\omega _\omega ^{CK,\,r}}}$ generated over an index stage ${L_\gamma }$ is recognizable. Finally, the techniques developed along the way allow us to prove that the halting number for ITRMs is recognizable and that the set of ITRM-computable reals is not ITRM-decidable.