Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T14:44:29.330Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMAL RESULTS ON RECOGNIZABILITY FOR INFINITE TIME REGISTER MACHINES

Published online by Cambridge University Press:  22 December 2015

MERLIN CARL
MERLIN CARL*
Affiliation:
FACHBEREICH MATHEMATIK UND STATISTIK UNIVERSITÄT KONSTANZ 78457 KONSTANZ GERMANYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Exploring further the properties of ITRM-recognizable reals started in [1], we provide a detailed analysis of recognizable reals and their distribution in Gödels constructible universe L. In particular, we show that new unrecognizable reals are generated at every index 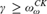$\gamma \, \ge \,\omega _\omega ^{CK}$. We give a machine-independent characterization of recognizability by proving that a real r is recognizable if and only if it is 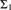${\Sigma _1}$-definable over 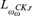${L_{\omega _\omega ^{CK,\,r}}}$ and that 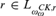$r\, \in \,{L_{\omega _\omega ^{CK,\,r}}}$ for every recognizable real r and show that either every or no r with 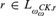$r\, \in \,{L_{\omega _\omega ^{CK,\,r}}}$ generated over an index stage ${L_\gamma }$ is recognizable. Finally, the techniques developed along the way allow us to prove that the halting number for ITRMs is recognizable and that the set of ITRM-computable reals is not ITRM-decidable.

Keywords

03D6503D6003Exx03E45Infinite Time ComputabilityGeneralized ComputabilityInfinite Time Register MachinesRecognizable Reals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1116 - 1130
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Carl, M., The distribution of ITRM-recognizable reals. Annals of Pure and Applied Logic, special issue for the CiE 2012, vol. 165 (2012), no. 9, pp. 1403–1417.CrossRefGoogle Scholar
Chong, C.T., A recursion-theoretic characterization of constructible reals. Bulletin of the London Mathematical Society, vol. 9 (1977), pp. 241–24.CrossRefGoogle Scholar
Cutland, N., Computability. An introduction to recursive function theory, Cambridge University Press, Cambridge, 1980.Google Scholar
Gitman, V., Hamkins, J.D., and Johnstone, T. A., What is the theory ZFC without power set? arXiv:1110.2430 [math.LO].Google Scholar
Hamkins, J. and Lewis, A., Infinite Time Turing Machines, this Journal, vol. 65 (2000), vol. 2, pp. 567–604.Google Scholar
Carl, M., Fischbach, T., Koepke, P., Miller, R., Nasfi, M., and Weckbecker, G., The basic theory of infinite time register machines. Archive for Mathematical Logic, vol. 49 (2010), no. 2, pp. 249–273.CrossRefGoogle Scholar
Jensen, R. and Karp, C., Primitive Recursive Set Functions, Proceedings of Symposia in Pure Mathematics, vol. XIII, Part 1 (1971), pp. 143–176.Google Scholar
Koepke, P., Ordinal Computability, Mathematical Theory and Computational Practice (Ambos-Spies, K. et al. , editors), Lecture Notes in Computer Science, vol. 5635 (2009), pp. 280–289, pp. 143–176CrossRefGoogle Scholar
Koepke, P. and Miller, Russell, An enhanced theory of infinite time register machines, Logic and Theory of Algorithms (Beckmann, A. et al. , editors), Lecture Notes in Computer Science, vol. 5028 (2008), pp. 306–315.CrossRefGoogle Scholar
Kunen, K., Set Theory - An Introduction to Independence Proofs, Elsevier, Amsterdam, 1980.Google Scholar
Mathias, A.R.D., Provident sets and rudimentary set forcing, Fundamenta Mathematicae, to appear.Google Scholar
Sacks, G., Countable admissible ordinals and hyperdegrees. Advances in Mathematics, vol. 19 (1976), pp. 213–262.CrossRefGoogle Scholar