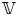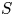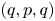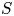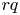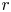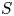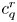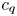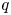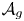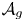1. Introduction
Let ![]() $G$ be a semi-simple Lie group and let
$G$ be a semi-simple Lie group and let ![]() $\Gamma \subset G$ be a lattice. Homogeneous dynamics is traditionally interested in the equidistribution properties of the orbits of a Lie subgroup
$\Gamma \subset G$ be a lattice. Homogeneous dynamics is traditionally interested in the equidistribution properties of the orbits of a Lie subgroup ![]() $H$ acting on
$H$ acting on ![]() $\Gamma \backslash G$ by right multiplication and, dually, on the dynamics of the left action of
$\Gamma \backslash G$ by right multiplication and, dually, on the dynamics of the left action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $G/H$. Classifying the closure of orbits of such actions is the subject of an extensive body of literature with far-reaching applications to number theory and ergodic theory.
$G/H$. Classifying the closure of orbits of such actions is the subject of an extensive body of literature with far-reaching applications to number theory and ergodic theory.
In this paper, our first purpose is to provide a fairly general answer to the following question.
Question 1 Assume that a sequence of closed ![]() $H$-orbits is equidistributed in
$H$-orbits is equidistributed in ![]() $\Gamma \backslash G$. Can we deduce an equidistribution result for the intersection of these
$\Gamma \backslash G$. Can we deduce an equidistribution result for the intersection of these ![]() $H$-orbits with a fixed analytic subvariety
$H$-orbits with a fixed analytic subvariety ![]() $V\subset \Gamma \backslash G$?
$V\subset \Gamma \backslash G$?
We consider more generally the following setting: let ![]() $G$ be a real semi-simple Lie group,
$G$ be a real semi-simple Lie group, ![]() $\Gamma$ a lattice in
$\Gamma$ a lattice in ![]() $G$,
$G$, ![]() $H$ a semi-simple subgroup of
$H$ a semi-simple subgroup of ![]() $G$,
$G$, ![]() $K$ a compact subgroup of
$K$ a compact subgroup of ![]() $G$ (which is not assumed to be maximal), and
$G$ (which is not assumed to be maximal), and ![]() $L= H\cap K$. Denote by
$L= H\cap K$. Denote by ![]() $p$ the projection map
$p$ the projection map ![]() $G/L\rightarrow G/H$ and by
$G/L\rightarrow G/H$ and by ![]() $\pi$ the projection map
$\pi$ the projection map ![]() $G/L\rightarrow G/K$. We fix compatible choices of invariant volume forms
$G/L\rightarrow G/K$. We fix compatible choices of invariant volume forms ![]() $\omega _{G}$,
$\omega _{G}$, ![]() $\omega _{G/H}$, and
$\omega _{G/H}$, and ![]() $\omega _{H}$ on
$\omega _{H}$ on ![]() $G$,
$G$, ![]() $G/H$, and
$G/H$, and ![]() $H$, respectively (see § 2.3).
$H$, respectively (see § 2.3).
Let ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ be a sequence of finite unions of closed
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ be a sequence of finite unions of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. As
$\Gamma \backslash G$. As ![]() $H$ is semi-simple,
$H$ is semi-simple, ![]() $\mathcal {O}_n$ has finite volume with respect to the volume form
$\mathcal {O}_n$ has finite volume with respect to the volume form ![]() $\omega _H$ along
$\omega _H$ along ![]() $H$-orbits for every
$H$-orbits for every ![]() $n\in \mathbb {N}$. We say that the sequence
$n\in \mathbb {N}$. We say that the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $\Gamma \backslash G$ if the normalized integration measureFootnote 1 on
$\Gamma \backslash G$ if the normalized integration measureFootnote 1 on ![]() $(\mathcal {O}_n,\omega _H)$ converges weakly to the Haar measure
$(\mathcal {O}_n,\omega _H)$ converges weakly to the Haar measure ![]() $\omega _G$ on
$\omega _G$ on ![]() $\Gamma \backslash G$.
$\Gamma \backslash G$.
Now let ![]() $S$ be a real analytic subvariety of
$S$ be a real analytic subvariety of ![]() $\Gamma \backslash G/K$ of codimension
$\Gamma \backslash G/K$ of codimension ![]() $\dim (H/L)$ whose smooth locus is oriented. Denote by
$\dim (H/L)$ whose smooth locus is oriented. Denote by ![]() $\mu _{S\cap \pi (\mathcal {O}_n)}$ the transverse intersection measure of
$\mu _{S\cap \pi (\mathcal {O}_n)}$ the transverse intersection measure of ![]() $V$ and
$V$ and ![]() $\mathcal {O}_n$, which counts (with an orientation sign and multiplicity) the transverse intersection points between
$\mathcal {O}_n$, which counts (with an orientation sign and multiplicity) the transverse intersection points between ![]() $S$ and
$S$ and ![]() $\pi (\mathcal {O}_n)$ (see § 3.2 for precisions). We prove the following.
$\pi (\mathcal {O}_n)$ (see § 3.2 for precisions). We prove the following.
Theorem 1.1 Assume that the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $\Gamma \backslash G$. Then the sequence of signed measures
$\Gamma \backslash G$. Then the sequence of signed measures ![]() $({1}/{\operatorname {Vol}(\mathcal {O}_n)})\mu _{S\cap \pi (\mathcal {O}_n)}$ on
$({1}/{\operatorname {Vol}(\mathcal {O}_n)})\mu _{S\cap \pi (\mathcal {O}_n)}$ on ![]() $S$ converges weakly to the restriction of the
$S$ converges weakly to the restriction of the ![]() $G$-invariant form
$G$-invariant form
This general result has countless potential applications, some of which will be detailed in the paper. What is interesting about this theorem is that the pull–push form ![]() $\pi _*p^*\omega _{G/H}$ is not easy, in general, to determine precisely and depends greatly on the subgroup
$\pi _*p^*\omega _{G/H}$ is not easy, in general, to determine precisely and depends greatly on the subgroup ![]() $H$. These forms were studied extensively by the second author in [Reference TholozanTho15] with a very different motivation. Building on this previous work, we will give tools to analyze this pull–push form and characterize it in various examples.
$H$. These forms were studied extensively by the second author in [Reference TholozanTho15] with a very different motivation. Building on this previous work, we will give tools to analyze this pull–push form and characterize it in various examples.
It sometimes happens that the form ![]() $\pi _*p^*\omega _{G/H}$ vanishes (this vanishing played an important role in [Reference TholozanTho15]). In that case, our theorem only asserts that positive and negative intersection points ‘cancel each other’ asymptotically.
$\pi _*p^*\omega _{G/H}$ vanishes (this vanishing played an important role in [Reference TholozanTho15]). In that case, our theorem only asserts that positive and negative intersection points ‘cancel each other’ asymptotically.
The theorem is stronger when ![]() $G/K$,
$G/K$, ![]() $H/L$, and
$H/L$, and ![]() $S$ are complex analytic. Then, all intersections are counted positively and the form
$S$ are complex analytic. Then, all intersections are counted positively and the form ![]() $\pi _*p^*\omega _{G/H}$ does not vanish (see Corollary 4.6). It vanishes in restriction to
$\pi _*p^*\omega _{G/H}$ does not vanish (see Corollary 4.6). It vanishes in restriction to ![]() $S$ if and only if all the intersections
$S$ if and only if all the intersections ![]() $S\cap \mathcal {O}_n$ have ‘exceptional dimension’ (i.e. complex dimension
$S\cap \mathcal {O}_n$ have ‘exceptional dimension’ (i.e. complex dimension ![]() $\geq 1$).
$\geq 1$).
In the applications we develop in the next sections, ![]() $H/L\subset G/K$ will be Mumford–Tate domains of Hodge structures and
$H/L\subset G/K$ will be Mumford–Tate domains of Hodge structures and ![]() $S\rightarrow \Gamma \backslash G/K$ is the period map of a polarized variation of Hodge structure. In Proposition 5.9, we give an algebraic characterization of when the form
$S\rightarrow \Gamma \backslash G/K$ is the period map of a polarized variation of Hodge structure. In Proposition 5.9, we give an algebraic characterization of when the form ![]() $\pi _*p^*\omega _{G/H}$ is non-zero in restriction to some analytic variation of Hodge structure.
$\pi _*p^*\omega _{G/H}$ is non-zero in restriction to some analytic variation of Hodge structure.
1.1 Equidistribution of typical Hodge loci
One of the main motivations of Theorem 1.1 is its application to the equidistribution of Hodge loci of variations of Hodge structure. In fact, the present paper is a continuation of the first author's previous work [Reference TayouTay20], which studied the particular case of the Noether–Lefschetz locus of a one-parameter family of K3 surfaces.
Let ![]() $\mathbb {V}=\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a polarized variation of Hodge structure (
$\mathbb {V}=\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a polarized variation of Hodge structure (![]() $\mathbb {Z}$-PVHS) of weight
$\mathbb {Z}$-PVHS) of weight ![]() $2k$ over a complex quasi-projective algebraic variety
$2k$ over a complex quasi-projective algebraic variety ![]() $S$ of dimension
$S$ of dimension ![]() $d\geq 1$ (see § 5). The group of Hodge classes
$d\geq 1$ (see § 5). The group of Hodge classes ![]() $\operatorname {Hdg}(s)$ at a point
$\operatorname {Hdg}(s)$ at a point ![]() $s$ is the free abelian group
$s$ is the free abelian group ![]() $\mathbb {V}_{\mathbb {Z},s} \cap \mathcal {F}^k\mathcal {V}_s$. An important class of examples of
$\mathbb {V}_{\mathbb {Z},s} \cap \mathcal {F}^k\mathcal {V}_s$. An important class of examples of ![]() $\mathbb {Z}$-PVHS is provided by those of geometric origin: starting from a smooth projective morphism
$\mathbb {Z}$-PVHS is provided by those of geometric origin: starting from a smooth projective morphism ![]() $f:X\rightarrow S$ where
$f:X\rightarrow S$ where ![]() $S$ is a smooth complex quasi-projective variety, the
$S$ is a smooth complex quasi-projective variety, the ![]() $2k$th cohomology groups of the fibers, modulo torsion, endowed with their Hodge structure give rise to a
$2k$th cohomology groups of the fibers, modulo torsion, endowed with their Hodge structure give rise to a ![]() $\mathbb {Z}$-PVHS of weight
$\mathbb {Z}$-PVHS of weight ![]() $2k$ on
$2k$ on ![]() $S$, see [Reference VoisinVoi02, Partie III] for more details.
$S$, see [Reference VoisinVoi02, Partie III] for more details.
More generally, let ![]() $\mathbb {V}^{\otimes }$ be the countable direct sum of
$\mathbb {V}^{\otimes }$ be the countable direct sum of ![]() $\mathbb {Z}$-PVHS
$\mathbb {Z}$-PVHS ![]() $\bigoplus _{a,b\geq 0} \mathbb {V}^{a}\otimes (\mathbb {V}^{\vee })^{b}$, where
$\bigoplus _{a,b\geq 0} \mathbb {V}^{a}\otimes (\mathbb {V}^{\vee })^{b}$, where ![]() $\mathbb {V}^{\vee }$ is the dual
$\mathbb {V}^{\vee }$ is the dual ![]() $\mathbb {Z}$-PVHS. Then the Hodge locus
$\mathbb {Z}$-PVHS. Then the Hodge locus ![]() $HL(S,\mathbb {V}^{\otimes })$ is defined as the subset
$HL(S,\mathbb {V}^{\otimes })$ is defined as the subset ![]() $s\in S$ where
$s\in S$ where ![]() $\mathbb {V}_s$ has more Hodge tensors than the very general fiber
$\mathbb {V}_s$ has more Hodge tensors than the very general fiber ![]() $\mathbb {V}_{s'}$. It is a countable union of algebraic subvarieties by [Reference Cattani, Deligne and KaplanCDK95, Reference Bakker, Klingler and TsimermanBKT20].
$\mathbb {V}_{s'}$. It is a countable union of algebraic subvarieties by [Reference Cattani, Deligne and KaplanCDK95, Reference Bakker, Klingler and TsimermanBKT20].
In this paper, we give a precise description of the typical part of this Hodge locus. More precisely, let ![]() $G$ be the generic Mumford–Tate group of the variation. The Hodge locus can also be seen as the locus of points of
$G$ be the generic Mumford–Tate group of the variation. The Hodge locus can also be seen as the locus of points of ![]() $S$ where the Mumford–Tate group is strictly contained in
$S$ where the Mumford–Tate group is strictly contained in ![]() $G$.
$G$.
For ![]() $H\subset G$ a sub-Mumford–Tate group, the typical Hodge locus for
$H\subset G$ a sub-Mumford–Tate group, the typical Hodge locus for ![]() $H$ is the set of points
$H$ is the set of points ![]() $s\in HL(S,\mathbb {V}^{\otimes })$ whose Mumford–Tate group is contained in
$s\in HL(S,\mathbb {V}^{\otimes })$ whose Mumford–Tate group is contained in ![]() $H$ and such that
$H$ and such that ![]() $\pi ^*p_*\omega _{G/H,s}\neq 0$. The typical Hodge locus is then the union of typical Hodge loci over all Mumford–Tate subgroups
$\pi ^*p_*\omega _{G/H,s}\neq 0$. The typical Hodge locus is then the union of typical Hodge loci over all Mumford–Tate subgroups ![]() $H$.
$H$.
We prove then the following theorem, see Proposition 5.9.
Theorem 1.2 The following statements are equivalent.
(i) There exists
 $H\subseteq G$ such that the typical Hodge locus for
$H\subseteq G$ such that the typical Hodge locus for  $H$ is equidistributed with respect to
$H$ is equidistributed with respect to  $\pi _*p^* \omega _{G/H}$ and in particular analytically dense.
$\pi _*p^* \omega _{G/H}$ and in particular analytically dense.(ii) There exists
 $H\subseteq G$ and one point
$H\subseteq G$ and one point  $s\in S$ such that
$s\in S$ such that  $\pi _*p^* \omega _{G/H}$ is non-zero at
$\pi _*p^* \omega _{G/H}$ is non-zero at  $x$.
$x$.(iii) The typical Hodge locus is non-empty.
Remark 1.3 The equidistribution assertion in this theorem as well as in all the subsequent theorems in this article, when not explicitly specified, should be understood in the sense of Theorem 1.1.
Remark 1.4 In the case of the Noether–Lefschetz loci, the theorem is a strengthening of the classical criterion of Green, see [Reference VoisinVoi02, Proposition 17.20].
The following proposition gives a criterion for the emptiness of the typical Hodge locus, see Proposition 5.11.
Proposition 1.5 If for every sub-Mumford–Tate group ![]() $H\subseteq G$ the Hodge structure
$H\subseteq G$ the Hodge structure ![]() $\mathfrak {g}/\mathfrak {h}$ satisfies
$\mathfrak {g}/\mathfrak {h}$ satisfies
then the typical Hodge locus is empty.
Theorem 1.2 will be applied to situations where we know how to compute the form ![]() $\pi _*p^* \omega _{G/H}$. These applications are explained in the next section.
$\pi _*p^* \omega _{G/H}$. These applications are explained in the next section.
Theorem 1.2 and Proposition 1.5 have also been independently studied by Baldi, Klingler, and Ullmo [Reference Baldi, Klingler and UllmoBKU21], see also the prior work of Klingler and Otwinowska [Reference Klingler and OtwinowskaKO21]. Moreover, the authors proved in [Reference Baldi, Klingler and UllmoBKU21, Theorem 2.3] that the condition in Proposition 1.5 is always satisfied whenever ![]() $\mathbb {V}$ has level more than three.
$\mathbb {V}$ has level more than three.
1.2 Applications
We explain now further applications of our main theorem. They correspond to situations where we know how to compute the pull–push form and they are hence far from exhaustive.
1.2.1 Refined Noether–Lefschetz loci
Let ![]() $\mathbb {V}$ be a polarized variation of Hodge structure of weight two over a complex quasi-projective algebraic variety
$\mathbb {V}$ be a polarized variation of Hodge structure of weight two over a complex quasi-projective algebraic variety ![]() $S$ of dimension
$S$ of dimension ![]() $d\geq 1$. Let
$d\geq 1$. Let ![]() $(q,p,q)$ be the Hodge numbers.
$(q,p,q)$ be the Hodge numbers.
Without loss of generality, one can assume that the ![]() $\mathbb {Z}$-PVHS is simple, so that the group of Hodge classes at a generic point is zero. The Noether–Lefschetz locus is then defined as the subset of elements of
$\mathbb {Z}$-PVHS is simple, so that the group of Hodge classes at a generic point is zero. The Noether–Lefschetz locus is then defined as the subset of elements of ![]() $S$ which admit non-trivial Hodge classes. More generally, we define the refined Noether–Lefschetz locus of rank
$S$ which admit non-trivial Hodge classes. More generally, we define the refined Noether–Lefschetz locus of rank ![]() $r$ as the subset where the group of Hodge classes has rank at least
$r$ as the subset where the group of Hodge classes has rank at least ![]() $r$, and denote it by
$r$, and denote it by ![]() $NL^{\geq r}(S)$.
$NL^{\geq r}(S)$.
Let ![]() $(V_\mathbb {Z},B)$ be the fiber of
$(V_\mathbb {Z},B)$ be the fiber of ![]() $\mathbb {V}$ at a point
$\mathbb {V}$ at a point ![]() $s\in S$. The period domain associated with
$s\in S$. The period domain associated with ![]() $\mathbb {V}$ is the homogeneous space
$\mathbb {V}$ is the homogeneous space ![]() $\mathcal {D}= G/K$, where
$\mathcal {D}= G/K$, where ![]() $G$ is the real group
$G$ is the real group ![]() $\operatorname {SO}(B)$ and
$\operatorname {SO}(B)$ and ![]() $K$ the stabilizer of the Hodge structure at
$K$ the stabilizer of the Hodge structure at ![]() $s$, and
$s$, and ![]() $S$ has a period map to the quotient
$S$ has a period map to the quotient ![]() $\Gamma \backslash \mathcal {D}$, where
$\Gamma \backslash \mathcal {D}$, where ![]() $\Gamma$ is the subgroup of
$\Gamma$ is the subgroup of ![]() $G$ preserving
$G$ preserving ![]() $V_\mathbb {Z}$. For our purposes, we assume that
$V_\mathbb {Z}$. For our purposes, we assume that ![]() $\mathbb {V}$ has generically immersive period map. Otherwise, we can replace
$\mathbb {V}$ has generically immersive period map. Otherwise, we can replace ![]() $S$ by its image by the period map, which still has an algebraic structure by [Reference Bakker, Brunebarbe and TsimermanBBT18].
$S$ by its image by the period map, which still has an algebraic structure by [Reference Bakker, Brunebarbe and TsimermanBBT18].
The refined Noether–Lefschetz locus of rank ![]() $r$ is a countable union of algebraic subvarieties which are the intersection of
$r$ is a countable union of algebraic subvarieties which are the intersection of ![]() $S$ with certain Mumford–Tate subdomains obtained as projections of right
$S$ with certain Mumford–Tate subdomains obtained as projections of right ![]() $H$-orbits for the subgroup
$H$-orbits for the subgroup ![]() $H$ of
$H$ of ![]() $G$ stabilizing a set of
$G$ stabilizing a set of ![]() $r$ integral elements in
$r$ integral elements in ![]() $V_\mathbb {Z}$ with positive intersection matrix. Applying Theorem 1.1 in this setting, we obtain equidistribution results for refined Noether–Lefschetz loci.
$V_\mathbb {Z}$ with positive intersection matrix. Applying Theorem 1.1 in this setting, we obtain equidistribution results for refined Noether–Lefschetz loci.
For all ![]() $n\in \mathbb {N}_{>0}$, define
$n\in \mathbb {N}_{>0}$, define ![]() $NL^{\geq r}(n)$ as the set of points
$NL^{\geq r}(n)$ as the set of points ![]() $s$ such that
$s$ such that ![]() $(\operatorname {Hdg}(s),B)$ contains a primitive sublattice of rank
$(\operatorname {Hdg}(s),B)$ contains a primitive sublattice of rank ![]() $r$ in restriction to which
$r$ in restriction to which ![]() $B$ has discriminant at most
$B$ has discriminant at most ![]() $n$. The set
$n$. The set ![]() $NL^{\geq r}(n)$ is an algebraic subvariety of
$NL^{\geq r}(n)$ is an algebraic subvariety of ![]() $S$. It has expected dimension
$S$. It has expected dimension ![]() $d-rq$ but can contain higher-dimensional components.
$d-rq$ but can contain higher-dimensional components.
Theorem 1.6 Let ![]() $\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a simple
$\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a simple ![]() $\mathbb {Z}$-PVHS of weight two and Hodge numbers
$\mathbb {Z}$-PVHS of weight two and Hodge numbers ![]() $(q,p,q)$ over a complex analytic variety
$(q,p,q)$ over a complex analytic variety ![]() $S$ of dimension
$S$ of dimension ![]() $d=rq$ and which has generically immersive period map. If
$d=rq$ and which has generically immersive period map. If ![]() $r\leq p$, then there is a constant
$r\leq p$, then there is a constant ![]() $\lambda >0$ such that, for every relatively compact open subset
$\lambda >0$ such that, for every relatively compact open subset ![]() $\Omega \subset S$ with boundary of measure zero, we have
$\Omega \subset S$ with boundary of measure zero, we have
where ![]() $c_q$ denotes the
$c_q$ denotes the ![]() $q$th Chern form of the bundle
$q$th Chern form of the bundle ![]() $\mathcal {F}^2\mathcal {V}$ endowed with the Hodge metric.
$\mathcal {F}^2\mathcal {V}$ endowed with the Hodge metric.
This theorem relies on an ‘elementary’ equidistribution result for positive-definite sublattices of a quadratic lattice that we prove in § 6.1. Using a more refined equidistribution result of Eskin and Oh [Reference Eskin and OhEO06b] based on Ratner theory, one can get a more precise equidistribution theorem for the locus where the Néron–Severi group is a fixed quadratic lattice. For a positive-definite matrix ![]() $M$, we denote by
$M$, we denote by ![]() $\mu _1(M)$ the square root of the smallest non-zero value integrally represented by
$\mu _1(M)$ the square root of the smallest non-zero value integrally represented by ![]() $M$. Say also that
$M$. Say also that ![]() $M$ is primitively represented by
$M$ is primitively represented by ![]() $(V_\mathbb {Z},B)$ if there exists a primitive sublattice of
$(V_\mathbb {Z},B)$ if there exists a primitive sublattice of ![]() $V_\mathbb {Z}$ of rank
$V_\mathbb {Z}$ of rank ![]() $r$ having a basis with intersection matrix equal to
$r$ having a basis with intersection matrix equal to ![]() $M$.
$M$.
Theorem 1.7 Let ![]() $\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a simple
$\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a simple ![]() $\mathbb {Z}$-PVHS of weight two and Hodge numbers
$\mathbb {Z}$-PVHS of weight two and Hodge numbers ![]() $(q,p,q)$ over a complex analytic variety
$(q,p,q)$ over a complex analytic variety ![]() $S$ of dimension
$S$ of dimension ![]() $d=rq$ and which has generically immersive period map. Assume that
$d=rq$ and which has generically immersive period map. Assume that ![]() $p,2q\geq 2$ and
$p,2q\geq 2$ and ![]() $rq< p$.
$rq< p$.
Let ![]() $(M_n)_{n\in \mathbb {N}}$ be a sequence of positive-definite integral matrices of rank
$(M_n)_{n\in \mathbb {N}}$ be a sequence of positive-definite integral matrices of rank ![]() $r$ which are primitively represented by
$r$ which are primitively represented by ![]() $(V_\mathbb {Z},B)$ and such that
$(V_\mathbb {Z},B)$ and such that ![]() $\mu _{1}(M_n)\rightarrow \infty$, as
$\mu _{1}(M_n)\rightarrow \infty$, as ![]() $n\rightarrow \infty$. Then there exists a sequence
$n\rightarrow \infty$. Then there exists a sequence ![]() $(a(M_n))_{n\in \mathbb {N}}$ of positive real numbers such that, for every relatively compact open subset
$(a(M_n))_{n\in \mathbb {N}}$ of positive real numbers such that, for every relatively compact open subset ![]() $\Omega \subset S$ with boundary of measure
$\Omega \subset S$ with boundary of measure ![]() $0$, we have
$0$, we have
Remark 1.8 In these theorems, one needs to exclude the points belonging to exceptional components of ![]() $NL^{\geq r}(S)$ of dimension at least one from the counting, i.e. the non-typical ones. The precise versions of these theorems are given in § 6.1.3.
$NL^{\geq r}(S)$ of dimension at least one from the counting, i.e. the non-typical ones. The precise versions of these theorems are given in § 6.1.3.
Remark 1.9 The Siegel–Weil formula gives an arithmetic expression for the asymptotic behavior of the sequence ![]() $a(M_n)$ in Theorem 1.7. The precise expression and how it grows with
$a(M_n)$ in Theorem 1.7. The precise expression and how it grows with ![]() $\det (M_n)$ are discussed in Lemma 6.7.
$\det (M_n)$ are discussed in Lemma 6.7.
Remark 1.10 A base of dimension ![]() $rq$ is the minimal dimension for which a refined Noether–Lefschetz locus is expected to exist for dimension reasons. If the dimension of the base
$rq$ is the minimal dimension for which a refined Noether–Lefschetz locus is expected to exist for dimension reasons. If the dimension of the base ![]() $S$ is greater than
$S$ is greater than ![]() $rq$, then Theorem 1.7 gives the equidistribution of
$rq$, then Theorem 1.7 gives the equidistribution of ![]() $NL^{\geq r}(S)$ towards
$NL^{\geq r}(S)$ towards ![]() $c_q(\mathcal {F}^2 \mathcal {V})^r$ in terms of currents (see Theorem 3.7).
$c_q(\mathcal {F}^2 \mathcal {V})^r$ in terms of currents (see Theorem 3.7).
Remark 1.11 As soon as ![]() $q\geq 2$, Griffiths’ transversality combined with the integrability condition of the tangent space to
$q\geq 2$, Griffiths’ transversality combined with the integrability condition of the tangent space to ![]() $S$ imply that the dimension of
$S$ imply that the dimension of ![]() $S$ is at most
$S$ is at most ![]() ${pq}/{2}$ by [Reference CarlsonCarl86, Theorem 1.1].
${pq}/{2}$ by [Reference CarlsonCarl86, Theorem 1.1].
Remark 1.12 These theorems are already interesting when ![]() $r=1$, for which they give the equidistribution of the Noether–Lefschetz locus. The case
$r=1$, for which they give the equidistribution of the Noether–Lefschetz locus. The case ![]() $r=q=1$ was treated by the first author in [Reference TayouTay20].
$r=q=1$ was treated by the first author in [Reference TayouTay20].
Remark 1.13 If the base ![]() $S$ of the variation
$S$ of the variation ![]() $\mathbb {V}$ is a complex projective variety, one can apply Theorem 1.1 to
$\mathbb {V}$ is a complex projective variety, one can apply Theorem 1.1 to ![]() $\Omega =S$ and get an asymptotic estimate of the ‘growth’ of the Noether–Lefschetz locus of
$\Omega =S$ and get an asymptotic estimate of the ‘growth’ of the Noether–Lefschetz locus of ![]() $S$. We conjecture that the same estimate holds when
$S$. We conjecture that the same estimate holds when ![]() $S$ is quasi-projective of arbitrary dimension (which implies that
$S$ is quasi-projective of arbitrary dimension (which implies that ![]() $\int _S c_q(\mathcal {F}^2\mathcal {V})^r < +\infty$). The case
$\int _S c_q(\mathcal {F}^2\mathcal {V})^r < +\infty$). The case ![]() $q=r=1$ has been settled in [Reference TayouTay20]. One could hopefully obtain this global estimate by working with the cohomology of an appropriate compactification of
$q=r=1$ has been settled in [Reference TayouTay20]. One could hopefully obtain this global estimate by working with the cohomology of an appropriate compactification of ![]() $\Gamma \backslash G/K$. This raises more general questions that are beyond the scope of this paper.
$\Gamma \backslash G/K$. This raises more general questions that are beyond the scope of this paper.
Theorem 1.1 applies to families of algebraic varieties whenever one has a generic local Torelli theorem. This holds for families of abelian varieties, ![]() $K3$ surfaces, hyperkähler manifolds, and for projective hypersurfaces by the general result of [Reference DonagiDon83], which yields the following examples.
$K3$ surfaces, hyperkähler manifolds, and for projective hypersurfaces by the general result of [Reference DonagiDon83], which yields the following examples.
(i) Smooth quintic surfaces in
 $\mathbf {P}^3$ have Hodge numbers
The moduli space of quintic surfaces has dimension
$\mathbf {P}^3$ have Hodge numbers
The moduli space of quintic surfaces has dimension \[ h^{2,0} = 4, \quad h^{1,1} = 45. \]
\[ h^{2,0} = 4, \quad h^{1,1} = 45. \]
 $40$ and satisfies a generic Torelli theorem by [Reference DonagiDon83]. Thus, Theorems 1.6 and 1.7 give equidistribution results for the refined Noether–Lefschetz loci on the moduli space of quintic surfaces up to
$40$ and satisfies a generic Torelli theorem by [Reference DonagiDon83]. Thus, Theorems 1.6 and 1.7 give equidistribution results for the refined Noether–Lefschetz loci on the moduli space of quintic surfaces up to  $r=10$.
$r=10$.(ii) Cubic hypersurfaces in
 $\mathbf {P}^7$ have Hodge numbers
Thus, their cohomology in degree six is a Hodge structure of weight two. The moduli space of cubic hypersurfaces in
$\mathbf {P}^7$ have Hodge numbers
Thus, their cohomology in degree six is a Hodge structure of weight two. The moduli space of cubic hypersurfaces in \[ h^{6,0}=h^{5,1}=0,\quad h^{4,2}=8,\quad h^{3,3} = 178. \]
\[ h^{6,0}=h^{5,1}=0,\quad h^{4,2}=8,\quad h^{3,3} = 178. \]
 $\mathbf {P}^7$ has dimension
$\mathbf {P}^7$ has dimension  $56$ and satisfies the generic Torelli theorem [Reference DonagiDon83]. Thus, again Theorems 1.6 and 1.7 give equidistribution results for refined Hodge loci on the moduli space of cubic hypersurfaces of
$56$ and satisfies the generic Torelli theorem [Reference DonagiDon83]. Thus, again Theorems 1.6 and 1.7 give equidistribution results for refined Hodge loci on the moduli space of cubic hypersurfaces of  $\mathbf {P}^7$ up to
$\mathbf {P}^7$ up to  $r=7$.
$r=7$.
1.2.2 Hodge loci in Shimura varieties
For ![]() $g\geq 2$, let
$g\geq 2$, let ![]() $\mathcal {A}_g$ be the moduli space of principally polarized complex abelian varieties of dimension
$\mathcal {A}_g$ be the moduli space of principally polarized complex abelian varieties of dimension ![]() $g$. It is well-known that the smallest codimension of a special subvariety is
$g$. It is well-known that the smallest codimension of a special subvariety is ![]() $g-1$ and it is realized for example by
$g-1$ and it is realized for example by ![]() $\mathcal {A}_{g-1}\times \mathcal {A}_{1}$. It is then expected, see [Reference Baldi, Klingler and UllmoBKU21, Remark 2.16], that the Hodge locus is analytically dense in any Hodge generic subvariety of dimension at least
$\mathcal {A}_{g-1}\times \mathcal {A}_{1}$. It is then expected, see [Reference Baldi, Klingler and UllmoBKU21, Remark 2.16], that the Hodge locus is analytically dense in any Hodge generic subvariety of dimension at least ![]() $g-1$.
$g-1$.
As a partial answer, we have the following results. Let ![]() $\mathcal {F}^{1}\rightarrow \mathcal {A}_g$ be the Hodge bundle and let
$\mathcal {F}^{1}\rightarrow \mathcal {A}_g$ be the Hodge bundle and let ![]() $(c_{n}(\mathcal {F}^{1}))_{0\leq n\leq g}$ be its Chern forms with respect to the Hodge metric. For
$(c_{n}(\mathcal {F}^{1}))_{0\leq n\leq g}$ be its Chern forms with respect to the Hodge metric. For ![]() $1\leq k\leq g$, defineFootnote 2
$1\leq k\leq g$, defineFootnote 2
Then ![]() $s_k$ is a semi-positive form. We prove then the following result.
$s_k$ is a semi-positive form. We prove then the following result.
Theorem 1.14 Let ![]() $X\subseteq \mathcal {A}_g$ be a smooth subvariety. If the restriction of
$X\subseteq \mathcal {A}_g$ be a smooth subvariety. If the restriction of ![]() $s_k$ to
$s_k$ to ![]() $X$ is non-zero, then the locus of elements in
$X$ is non-zero, then the locus of elements in ![]() $X$ parameterizing abelian varieties containing a sub-abelian variety of dimension
$X$ parameterizing abelian varieties containing a sub-abelian variety of dimension ![]() $k$ is analytically dense and equidistributed with respect to
$k$ is analytically dense and equidistributed with respect to ![]() $s_k$. In particular, if
$s_k$. In particular, if ![]() $X$ is compact and has dimension at least
$X$ is compact and has dimension at least ![]() $({(g-1)(g-2)})/{2}$, then the Hodge locus is analytically dense in
$({(g-1)(g-2)})/{2}$, then the Hodge locus is analytically dense in ![]() $X$.
$X$.
If ![]() $k=1$, then the theorem yields that the Hodge locus is dense if
$k=1$, then the theorem yields that the Hodge locus is dense if ![]() $c_{g-1}$ is non-zero by restriction to
$c_{g-1}$ is non-zero by restriction to ![]() $X$. This prompts the following question.
$X$. This prompts the following question.
Question 1.15 Let ![]() $X$ be a Hodge generic subvariety of
$X$ be a Hodge generic subvariety of ![]() $\mathcal {A}_g$ of dimension at least
$\mathcal {A}_g$ of dimension at least ![]() $g-1$. Is the restriction of
$g-1$. Is the restriction of ![]() $c_{g-1}$ to
$c_{g-1}$ to ![]() $X$ always non-zero?
$X$ always non-zero?
Remark 1.16 The assumption of Hodge genericity is necessary. Indeed, if ![]() $X=\mathcal {A}_2\times \{pt\}\subseteq \mathcal {A}_4$. Then
$X=\mathcal {A}_2\times \{pt\}\subseteq \mathcal {A}_4$. Then ![]() $X$ has dimension
$X$ has dimension ![]() $3\geq 4-1=3$ but the restriction of
$3\geq 4-1=3$ but the restriction of ![]() $c_3$ to
$c_3$ to ![]() $X$ vanishes. Indeed, the restriction of the vector bundle
$X$ vanishes. Indeed, the restriction of the vector bundle ![]() $\mathcal {F}^1$ to
$\mathcal {F}^1$ to ![]() $X$ splits as a direct sum of two vector bundles of rank two, one of them being trivial. Hence,
$X$ splits as a direct sum of two vector bundles of rank two, one of them being trivial. Hence, ![]() $c_{3}$ vanishes on
$c_{3}$ vanishes on ![]() $X$.
$X$.
Theorem 1.14 admits the following generalization.
Theorem 1.17 Let ![]() $S$ be a connected Shimura variety associated to a connected Shimura datum
$S$ be a connected Shimura variety associated to a connected Shimura datum ![]() $(G,\mathcal {D})$. Assume that there exists a Shimura sub-datum
$(G,\mathcal {D})$. Assume that there exists a Shimura sub-datum ![]() $(H,\mathcal {D}_H)$ such that
$(H,\mathcal {D}_H)$ such that ![]() $\pi _*p^* \omega _{G/H}$ is positive of type
$\pi _*p^* \omega _{G/H}$ is positive of type ![]() $(k,k)$. Then the Hodge locus is dense in any subvariety of dimension at least
$(k,k)$. Then the Hodge locus is dense in any subvariety of dimension at least ![]() $k$ and equidistributed with respect to
$k$ and equidistributed with respect to ![]() $\pi _*p^* \omega _{G/H}$. In particular, if
$\pi _*p^* \omega _{G/H}$. In particular, if ![]() $G$ is absolutely simple and has a Shimura curve associated to a Shimura subgroup
$G$ is absolutely simple and has a Shimura curve associated to a Shimura subgroup ![]() $H$, then the Hodge locus is dense in any hypersurface and equidistributed with respect to
$H$, then the Hodge locus is dense in any hypersurface and equidistributed with respect to ![]() $\pi _*p^* \omega _{G/H}$.
$\pi _*p^* \omega _{G/H}$.
In particular, for unitary Shimura varieties, we obtain the following.
Corollary 1.18 Let ![]() $S$ be a Shimura variety of unitary type
$S$ be a Shimura variety of unitary type ![]() $(n,1)$. Then the typical Hodge locus is dense and equidistributed in any subvariety of
$(n,1)$. Then the typical Hodge locus is dense and equidistributed in any subvariety of ![]() $S$ of positive dimension.
$S$ of positive dimension.
Let ![]() $S$ be a Shimura variety associated with a connected Shimura datum
$S$ be a Shimura variety associated with a connected Shimura datum ![]() $(G,\mathcal {D}_H)$ and let
$(G,\mathcal {D}_H)$ and let ![]() $k$ be the minimal integer for which there exists a sub-Shimura datum
$k$ be the minimal integer for which there exists a sub-Shimura datum ![]() $(H,\mathcal {D}_H)$ such that
$(H,\mathcal {D}_H)$ such that ![]() $\pi _*p^*\omega _{G/H}$ is of type
$\pi _*p^*\omega _{G/H}$ is of type ![]() $(k,k)$. Then Question 1.15 has the following generalization.
$(k,k)$. Then Question 1.15 has the following generalization.
Question 1.19 Let ![]() $X\subset S$ be a Hodge generic subvariety of dimension at least
$X\subset S$ be a Hodge generic subvariety of dimension at least ![]() $k$. Is the restriction of
$k$. Is the restriction of ![]() $\pi _*p^*\omega _{G/H}$ to
$\pi _*p^*\omega _{G/H}$ to ![]() $X$ always non-zero?
$X$ always non-zero?
1.2.3 Equidistribution of families of CM points in Shimura varieties
Another application of Theorem 1.1 is an equidistribution result for families of CM points in some Shimura varieties. Several results about the equidistribution of CM points are known (see, for example, [Reference DukeDuk88, Reference ZhangZha05, Reference KhayutinKha19]) and, in general, the following conjecture is widely open (see [Reference YafaevYaf17, Conjecture 2.6] for more details on this conjecture).
Conjecture 1.20 Let ![]() $S$ be a Shimura variety over
$S$ be a Shimura variety over ![]() $\overline {\mathbb {Q}}$ and let
$\overline {\mathbb {Q}}$ and let ![]() $(x_n)_{n\in \mathbb {N}}$ be a generic sequence of CM points in
$(x_n)_{n\in \mathbb {N}}$ be a generic sequence of CM points in ![]() $S$. Then the sequence of Galois orbits
$S$. Then the sequence of Galois orbits ![]() $\mathrm {Aut}(\overline {\mathbb {Q}}/\mathbb {Q})\cdot x_n$ is equidistributed in
$\mathrm {Aut}(\overline {\mathbb {Q}}/\mathbb {Q})\cdot x_n$ is equidistributed in ![]() $S(\mathbb {C})$.
$S(\mathbb {C})$.
In what follows, we state the result we prove in the simplest case of Siegel Shimura varieties, referring to Theorem 6.17 for the most general statement.
Let ![]() $g\geq 1$. A polarized isogeny
$g\geq 1$. A polarized isogeny ![]() $f:(A_1,\omega _1)\rightarrow (A_2,\omega _2)$ of similitude factor
$f:(A_1,\omega _1)\rightarrow (A_2,\omega _2)$ of similitude factor ![]() $N\geq 1$ between two principally polarized abelian varieties of dimension
$N\geq 1$ between two principally polarized abelian varieties of dimension ![]() $g$ is an isogeny which satisfies
$g$ is an isogeny which satisfies ![]() $f^*\omega _2=N\,\omega _1$. If
$f^*\omega _2=N\,\omega _1$. If ![]() $A_1=A_2$, we say moreover that
$A_1=A_2$, we say moreover that ![]() $f$ is regular if the centralizer of the homological realization of
$f$ is regular if the centralizer of the homological realization of ![]() $f$ in
$f$ in ![]() $\mathrm {GSp}_{2g}(H^{1}(A,\mathbb {R}))$ is a torus. This implies that
$\mathrm {GSp}_{2g}(H^{1}(A,\mathbb {R}))$ is a torus. This implies that ![]() $A_1$ is a CM abelian variety,Footnote 3 meaning that
$A_1$ is a CM abelian variety,Footnote 3 meaning that ![]() $\mathrm {End}(A)_\mathbb {Q}$ is a commutative algebra of degree
$\mathrm {End}(A)_\mathbb {Q}$ is a commutative algebra of degree ![]() $2g$ over
$2g$ over ![]() $\mathbb {Q}$, i.e. the maximal possible dimension. Conversely, every CM polarized Abelian variety admits a regular self-isogeny (Lemma 6.16). An equivalent characterization of CM abelian varieties is that their Mumford–Tate group
$\mathbb {Q}$, i.e. the maximal possible dimension. Conversely, every CM polarized Abelian variety admits a regular self-isogeny (Lemma 6.16). An equivalent characterization of CM abelian varieties is that their Mumford–Tate group ![]() $MT(A)$ (which is contained in the centralizer of the isogeny
$MT(A)$ (which is contained in the centralizer of the isogeny ![]() $f$) is a torus, see Definition 6.12.
$f$) is a torus, see Definition 6.12.
Let ![]() $\omega$ be the first Chern form of the Hodge bundle on
$\omega$ be the first Chern form of the Hodge bundle on ![]() $\mathcal {A}_g$. It is well-known that
$\mathcal {A}_g$. It is well-known that ![]() $\omega$ is a Kähler form. If
$\omega$ is a Kähler form. If ![]() $A$ is a principally polarized abelian variety, we denote by
$A$ is a principally polarized abelian variety, we denote by ![]() ${\dagger} :\mathrm {End}(A)_\mathbb {Q}\rightarrow \mathrm {End}(A)_\mathbb {Q}$ the Rosati involution. As an application of Theorem 1.1, and of the main result of [Reference Clozel, Oh and UllmoCOU01] (see also [Reference Eskin and OhEO06a]), we get an equidistribution result for CM abelian varieties admitting self-isogenies of fixed degree.
${\dagger} :\mathrm {End}(A)_\mathbb {Q}\rightarrow \mathrm {End}(A)_\mathbb {Q}$ the Rosati involution. As an application of Theorem 1.1, and of the main result of [Reference Clozel, Oh and UllmoCOU01] (see also [Reference Eskin and OhEO06a]), we get an equidistribution result for CM abelian varieties admitting self-isogenies of fixed degree.
Theorem 1.21 There exists a sequence ![]() $b(N)$ such that, for every relatively compact open subset
$b(N)$ such that, for every relatively compact open subset ![]() $\Omega \subset \mathcal {A}_g$ with boundary of measure
$\Omega \subset \mathcal {A}_g$ with boundary of measure ![]() $0$, we have
$0$, we have
This theorem does not answer Conjecture 1.20 because, as ![]() $N$ grows, our equidistributing sets are the union of an increasing number of Galois orbits. It is however sharper than other more elementary equidistribution results. For comparison, in the case of
$N$ grows, our equidistributing sets are the union of an increasing number of Galois orbits. It is however sharper than other more elementary equidistribution results. For comparison, in the case of ![]() $g=1$, Conjecture 1.20 is answered positively by Duke's equidistribution theorem for CM elliptic curves with fundamental discriminant
$g=1$, Conjecture 1.20 is answered positively by Duke's equidistribution theorem for CM elliptic curves with fundamental discriminant ![]() $N$ [Reference DukeDuk88, Thereom 1] and by Clozel–Ullmo in general [Reference Clozel and UllmoCU04, Théorème 2.4], whereas an elementary counting argument easily gives the equidistribution of CM curves with discriminant at most
$N$ [Reference DukeDuk88, Thereom 1] and by Clozel–Ullmo in general [Reference Clozel and UllmoCU04, Théorème 2.4], whereas an elementary counting argument easily gives the equidistribution of CM curves with discriminant at most ![]() $N$. Our theorem lies in between: it asserts that the set of CM elliptic curves with discriminant of the form
$N$. Our theorem lies in between: it asserts that the set of CM elliptic curves with discriminant of the form ![]() $N-4a^2$ for all integers
$N-4a^2$ for all integers ![]() $0\leq a\leq \sqrt {N}$ is equidistributed when
$0\leq a\leq \sqrt {N}$ is equidistributed when ![]() $N$ goes to
$N$ goes to ![]() $+\infty$.
$+\infty$.
1.2.4 Equidistribution of Hecke translates
We mention two further applications of Theorem 1.1 that we obtain. The first is related to the dynamics of Hecke translates in ![]() $\mathcal {A}_g$.
$\mathcal {A}_g$.
Let ![]() $S$ and
$S$ and ![]() $D$ be two subvarieties of
$D$ be two subvarieties of ![]() $\mathcal {A}_g$ of complimentary dimensions such that
$\mathcal {A}_g$ of complimentary dimensions such that ![]() $S$ has dimension
$S$ has dimension ![]() $d\leq 2$. Let
$d\leq 2$. Let ![]() $\omega$ be as before the first Chern form of the Hodge bundle on
$\omega$ be as before the first Chern form of the Hodge bundle on ![]() $\mathcal {A}_g$. In addition, if
$\mathcal {A}_g$. In addition, if ![]() $(s,d)\in S\times D$, with corresponding abelian varieties
$(s,d)\in S\times D$, with corresponding abelian varieties ![]() $A_s$ and
$A_s$ and ![]() $A_d$, we denote by
$A_d$, we denote by ![]() $\mathrm {Isog}^N(A_s,A_d)$ the set of isogenies from
$\mathrm {Isog}^N(A_s,A_d)$ the set of isogenies from ![]() $A_s$ to
$A_s$ to ![]() $A_d$ of similitude factor
$A_d$ of similitude factor ![]() $N$. An isogeny
$N$. An isogeny ![]() $f:A_{s}\rightarrow A_d$ is said to be transverse, if it does not admit first-order deformations in
$f:A_{s}\rightarrow A_d$ is said to be transverse, if it does not admit first-order deformations in ![]() $S\times D$. Then we prove the following, see § 6.3 for more details.
$S\times D$. Then we prove the following, see § 6.3 for more details.
Theorem 1.22 There exists a sequence ![]() $(c(N))_{N\geq 1}$ of positive real numbers such that for every relatively compact open subsets
$(c(N))_{N\geq 1}$ of positive real numbers such that for every relatively compact open subsets ![]() $\Omega \subset S$,
$\Omega \subset S$, ![]() $\Omega '\subset D$ with boundary of measure zero, we have
$\Omega '\subset D$ with boundary of measure zero, we have
In particular, the locus of points in ![]() $S$ isogenous to a point in
$S$ isogenous to a point in ![]() $D$ is analytically dense and equidistributed in
$D$ is analytically dense and equidistributed in ![]() $S$.
$S$.
We have the following corollary.
Corollary 1.23 Let ![]() $S\subset \mathcal {A}_4$ be a curve. Then the locus of points in
$S\subset \mathcal {A}_4$ be a curve. Then the locus of points in ![]() $S$ isogenous to the Jacobian of a curve is analytically dense and equidistributed in
$S$ isogenous to the Jacobian of a curve is analytically dense and equidistributed in ![]() $S$.
$S$.
1.2.5 Equidistribution in cohomology
Theorem 1.1 yields that cohomology classes of ![]() $\Gamma \backslash G/K$ represented by an equidistributing sequence of locally homogeneous submanifolds converge after normalization to the cohomology class of a locally invariant form. (See Corollary 2.9 for a precise statement.)
$\Gamma \backslash G/K$ represented by an equidistributing sequence of locally homogeneous submanifolds converge after normalization to the cohomology class of a locally invariant form. (See Corollary 2.9 for a precise statement.)
To illustrate this in a specific example, we use the same notation as in § 1.2.1. Then we have a family of special cycles in ![]() $\Gamma \backslash G/K\simeq \Gamma \backslash \mathcal {D}$ where
$\Gamma \backslash G/K\simeq \Gamma \backslash \mathcal {D}$ where ![]() $\mathcal {D}$ is the period domain, defined as follows: for
$\mathcal {D}$ is the period domain, defined as follows: for ![]() $r\geq 1$,
$r\geq 1$, ![]() $\underline {\lambda }_0\in V_\mathbb {Z}^r$,
$\underline {\lambda }_0\in V_\mathbb {Z}^r$, ![]() $H=\mathrm {Stab}(\underline {\lambda }_0)$,
$H=\mathrm {Stab}(\underline {\lambda }_0)$, ![]() $M\in M_r(\mathbb {Z})$ semi-positive-definite matrix with rank
$M\in M_r(\mathbb {Z})$ semi-positive-definite matrix with rank ![]() $r(M)$, and
$r(M)$, and ![]() $V_M\overset {\text {def}}= \{\underline {\lambda }\in V_\mathbb {Z}^r,\,(B(\lambda _i\cdot\lambda _j))_{1\leq i,j\leq r}=M\}$, let
$V_M\overset {\text {def}}= \{\underline {\lambda }\in V_\mathbb {Z}^r,\,(B(\lambda _i\cdot\lambda _j))_{1\leq i,j\leq r}=M\}$, let
Let ![]() $c_q(\mathcal {F}^2\mathcal {V})$ be as before the top Chern form of the vector bundle
$c_q(\mathcal {F}^2\mathcal {V})$ be as before the top Chern form of the vector bundle ![]() $\mathcal {F}^2\mathcal {V}$.
$\mathcal {F}^2\mathcal {V}$.
Proposition 1.24 Let ![]() $(M_n)_{n\in \mathbb {N}}$ be a sequence of positive-definite matrices primitively represented by
$(M_n)_{n\in \mathbb {N}}$ be a sequence of positive-definite matrices primitively represented by ![]() $(V_\mathbb {Z},B)$ such that
$(V_\mathbb {Z},B)$ such that ![]() $\mu _1(M_n)\rightarrow \infty$, as
$\mu _1(M_n)\rightarrow \infty$, as ![]() $n\rightarrow \infty$. Then
$n\rightarrow \infty$. Then
This result is reminiscent of the work of Kudla–Millson on modularity of special cycles, see [Reference Kudla and MillsonKM90], see also [Reference GarciaGar18] for a recent approach using superconnections. Indeed, in both these papers, it is proved that the formal generating series:
is a Siegel modular form valued in ![]() $H^{2qr}(\Gamma \backslash \mathcal {D},\mathbb {R})$. Here
$H^{2qr}(\Gamma \backslash \mathcal {D},\mathbb {R})$. Here ![]() $\mathfrak {H}_r$ is the Siegel upper half space. Hence, the knowledge of the structure of the space of Siegel modular forms allows, in principle, an asymptotic formula of
$\mathfrak {H}_r$ is the Siegel upper half space. Hence, the knowledge of the structure of the space of Siegel modular forms allows, in principle, an asymptotic formula of ![]() $\mathcal {Z}(M)$ to be given in terms of the constant term
$\mathcal {Z}(M)$ to be given in terms of the constant term ![]() $c_q(\mathcal {F}^2\mathcal {V})^r$. As
$c_q(\mathcal {F}^2\mathcal {V})^r$. As ![]() $r$ grows, the structure of the space of Siegel modular forms becomes complicated to analyze and much work is needed to derive formulas similar to ours through this approach. Our method yields a straightforward estimate on the asymptotic growth of
$r$ grows, the structure of the space of Siegel modular forms becomes complicated to analyze and much work is needed to derive formulas similar to ours through this approach. Our method yields a straightforward estimate on the asymptotic growth of ![]() $\mathcal {Z}(M)$ without using these results. One might even hope that this asymptotic estimate could help understand the cusp structure of Kudla and Millson's modular forms.
$\mathcal {Z}(M)$ without using these results. One might even hope that this asymptotic estimate could help understand the cusp structure of Kudla and Millson's modular forms.
1.3 Related work
The distribution of the Hodge locus has been investigated independently and concomitantly by Baldi, Klingler, and Ullmo in [Reference Baldi, Klingler and UllmoBKU21]. In addition to striking results on the atypical Hodge locus (see also [Reference Klingler and OtwinowskaKO21] for prior work), they prove several properties about the typical Hodge locus that echo the present work, namely that the typical Hodge locus is either empty or dense, and is always empty when the level is at least three.
Several results analogous to Theorem 1.7 for algebraic families parameterized by Shimura varieties have been settled in arithmetic situations over rings of integers of number fields and over curves defined over finite fields: indeed Charles proved [Reference CharlesCha18] that there are infinitely many places where the reduction of two elliptic curves are isogenous; Shankar and Tang [Reference Shankar and TangST20] proved that an abelian surface over a number field with real multiplication has infinitely many specializations which are isogenous to the self-product of an elliptic curve and in collaboration with Maulik in [Reference Maulik, Shankar and TangMST22b] they derived similar results for ordinary abelian surfaces over the function field of a curve over a finite field. Finally the analogous statement of Theorem 1.7 for K3-type variations of Hodge structures over curves has been proved in the number field setting in [Reference Shankar, Shankar, Tang and TayouSSTT22, Reference TayouTay22] and over curves over finite fields in [Reference Maulik, Shankar and TangMST22a]. It is thus interesting to further explore other analogous statements of Theorems 1.1, 1.7, and 1.22 over number fields and function fields situations.
1.4 Organization of the paper
In § 2, we introduce the setting of homogeneous dynamics and explain how to reformulate an equidistribution theorem in terms of currents. In § 3, we deduce our general theorem for transverse intersections of locally homogeneous subspaces with a fixed analytic subvariety, proving Theorem 1.1. Section 4 is devoted to the study of the pull–push form. In particular, we explain how to interpret its cohomology class via compact duality of homogeneous spaces. In § 5, we discuss the pull–push forms in the case of period domains of variations of Hodge structures and relate them to Chern classes of Hodge bundles, allowing us to compute these forms explicitly in the setting of a variation of Hodge structure of weight two and Shimura varieties. Finally, in § 6, we discuss our applications: the study of refined Noether–Lefschetz loci, the equidistribution of some families of CM points in Shimura varieties and the equidistribution of intersection points of Hecke translates of the Torelli locus with a curve and a surface in ![]() $\mathcal {A}_g$.
$\mathcal {A}_g$.
2. Equidistribution in terms of currents
In this section, we recall some background on convergence of measures, currents, and homogeneous spaces. Then we reformulate equidistribution results in homogeneous dynamics in terms of weak convergence of currents. Finally, we recall some equidistribution results from Ratner's work.
2.1 Convergence of measures
Let us start by recalling a few classical facts in measure theory which are used mainly in § 3.
Let ![]() $S$ be an analytic subset of dimension
$S$ be an analytic subset of dimension ![]() $d$ of a manifold
$d$ of a manifold ![]() $M$ whose smooth locus is oriented, and let
$M$ whose smooth locus is oriented, and let ![]() $\omega$ be a smooth form of degree
$\omega$ be a smooth form of degree ![]() $d$ on
$d$ on ![]() $M$. Then the restriction of
$M$. Then the restriction of ![]() $\omega$ to the smooth locus of
$\omega$ to the smooth locus of ![]() $S$ defines a signed Radon measure on
$S$ defines a signed Radon measure on ![]() $S$. This measure is regular in the sense that:
$S$. This measure is regular in the sense that:
(i) for every open subset
 $U$ of
$U$ of  $S$ and every sequence of compact sets
$S$ and every sequence of compact sets  $(C_n)_{n\in \mathbb {N}}$ with
$(C_n)_{n\in \mathbb {N}}$ with  $C_n \subset \mathring {C}_{n+1}$ and
$C_n \subset \mathring {C}_{n+1}$ and  $\bigcup _{n\in \mathbb {N}} C_n = U$, we have
$\bigcup _{n\in \mathbb {N}} C_n = U$, we have
 \[ \int_U \omega = \lim_{n\to +\infty} \int_{C_n} \omega; \]
\[ \int_U \omega = \lim_{n\to +\infty} \int_{C_n} \omega; \]
(ii) for every compact subset
 $C\subset S$ and every sequence of open sets
$C\subset S$ and every sequence of open sets  $(U_n)_{n\in \mathbb {N}}$ with
$(U_n)_{n\in \mathbb {N}}$ with  $\bar U_{n+1} \subset U_n$ and
$\bar U_{n+1} \subset U_n$ and  $\bigcap _{n\in \mathbb {N}} U_n=C$, we have
$\bigcap _{n\in \mathbb {N}} U_n=C$, we have
 \[ \int_C \omega = \lim_{n\to +\infty} \int_{U_n} \omega. \]
\[ \int_C \omega = \lim_{n\to +\infty} \int_{U_n} \omega. \]
In the absence of any precision, we say that a set ![]() $A\subset S$ has measure zero if the intersection of
$A\subset S$ has measure zero if the intersection of ![]() $A$ with the smooth locus of
$A$ with the smooth locus of ![]() $S$ has Lebesgue measure zero in any coordinate chart. This implies that its measure with respect to
$S$ has Lebesgue measure zero in any coordinate chart. This implies that its measure with respect to ![]() $\omega$ is zero.
$\omega$ is zero.
Given a sequence of signed Radon measures ![]() $\mu _n$, we have the following equivalent characterizations of the convergence of
$\mu _n$, we have the following equivalent characterizations of the convergence of ![]() $\mu _n$ to
$\mu _n$ to ![]() $\omega$:
$\omega$:
(i) for every continuous function
 $f:S\to \mathbb {R}$ with compact support,
$f:S\to \mathbb {R}$ with compact support,
 \[ \mu_n(f) \underset{n\to +\infty}{\longrightarrow} \int_S f \omega; \]
\[ \mu_n(f) \underset{n\to +\infty}{\longrightarrow} \int_S f \omega; \]
(ii) for every relatively compact open subset
 $\Omega$ of
$\Omega$ of  $S$ with boundary of measure zero,
$S$ with boundary of measure zero,
 \[ \mu_n(\Omega) \underset{n\to +\infty}{\longrightarrow} \int_\Omega\omega. \]
\[ \mu_n(\Omega) \underset{n\to +\infty}{\longrightarrow} \int_\Omega\omega. \]
We then say that ![]() $\mu _n$ converges weakly to
$\mu _n$ converges weakly to ![]() $\omega$ and we write
$\omega$ and we write
We say that ![]() $\mu _n$ converges weakly to
$\mu _n$ converges weakly to ![]() $\omega$ on an open subset
$\omega$ on an open subset ![]() $U$ if the restriction of
$U$ if the restriction of ![]() $\mu _n$ to
$\mu _n$ to ![]() $U$ converges weakly to the restriction of
$U$ converges weakly to the restriction of ![]() $\omega$. Equivalently,
$\omega$. Equivalently, ![]() $\mu _n$ converges weakly to
$\mu _n$ converges weakly to ![]() $\omega$ on
$\omega$ on ![]() $U$ if property (i) holds for any function with compact support inside
$U$ if property (i) holds for any function with compact support inside ![]() $U$.
$U$.
The following standard facts will be useful in proving weak convergence of measures.
Proposition 2.1 Let ![]() $(U_i)_{i\in I}$ be an open covering of
$(U_i)_{i\in I}$ be an open covering of ![]() $S$. Then
$S$. Then ![]() $\mu _n$ converges weakly to
$\mu _n$ converges weakly to ![]() $\omega$ on
$\omega$ on ![]() $S$ if and only if converges weakly to
$S$ if and only if converges weakly to ![]() $\omega$ on
$\omega$ on ![]() $U_i$ for all
$U_i$ for all ![]() $i\in I$.
$i\in I$.
Proposition 2.2 Let ![]() $Z$ be a closed subset of
$Z$ be a closed subset of ![]() $S$ of measure
$S$ of measure ![]() $0$. Assume that
$0$. Assume that ![]() ${\mu _n}$ converges weakly to
${\mu _n}$ converges weakly to ![]() $\omega$ on
$\omega$ on ![]() $Z^c$. Then the following are equivalent:
$Z^c$. Then the following are equivalent:
(i)
 $\mu _n$ converges weakly to
$\mu _n$ converges weakly to  $\omega$ on
$\omega$ on  $S$;
$S$;(ii) for very compact subset
 $C \subset Z$ and every
$C \subset Z$ and every  $\epsilon >0$, there exists an open neighborhood
$\epsilon >0$, there exists an open neighborhood  $U_\epsilon$ of
$U_\epsilon$ of  $C$ such that
$C$ such that
 \[ \limsup_{n\to +\infty} \vert \mu_n\vert (U_\epsilon) \leq \epsilon. \]
\[ \limsup_{n\to +\infty} \vert \mu_n\vert (U_\epsilon) \leq \epsilon. \]
Here, ![]() $\vert \mu _n\vert = \mu _n^+ + \mu _n^-$ denotes the total variation measure of
$\vert \mu _n\vert = \mu _n^+ + \mu _n^-$ denotes the total variation measure of ![]() $\mu$.
$\mu$.
2.2 Currents on manifolds
For more details on this section, we refer to [Reference Griffiths and HarrisGH94, Chapter 3, § 1].
Let ![]() $M$ be a real manifold of dimension
$M$ be a real manifold of dimension ![]() $n$. For
$n$. For ![]() $k\geq 0$, let
$k\geq 0$, let ![]() $\Omega _{c}^{k}(M)$ be the vector space of
$\Omega _{c}^{k}(M)$ be the vector space of ![]() $C^{\infty }$ differential forms on
$C^{\infty }$ differential forms on ![]() $M$ of degree
$M$ of degree ![]() $k$ with compact support. It is endowed with its natural topological space structure making it a Fréchet space.
$k$ with compact support. It is endowed with its natural topological space structure making it a Fréchet space.
Definition 2.3 A current of degree ![]() $k$ on
$k$ on ![]() $M$ is a continuous linear form on
$M$ is a continuous linear form on ![]() $\Omega _{c}^{n-k}(M)$. The space of currents of degree
$\Omega _{c}^{n-k}(M)$. The space of currents of degree ![]() $k$ on
$k$ on ![]() $M$ is denoted by
$M$ is denoted by ![]() $\mathcal {D}^k(M)$.
$\mathcal {D}^k(M)$.
Example 2.4 If ![]() $N\hookrightarrow M$ is an oriented properly immersed submanifold of codimension
$N\hookrightarrow M$ is an oriented properly immersed submanifold of codimension ![]() $k$ of
$k$ of ![]() $M$, the integration current
$M$, the integration current ![]() $T_N\in \mathcal {D}^k(M)$ is defined by
$T_N\in \mathcal {D}^k(M)$ is defined by
Example 2.5 A differential ![]() $k$-form
$k$-form ![]() $\alpha$ induces a
$\alpha$ induces a ![]() $k$-dimensional current
$k$-dimensional current ![]() $T_\alpha$ defined by
$T_\alpha$ defined by
The exterior derivative ![]() $d$ on differential forms induces a map
$d$ on differential forms induces a map
defined by
A current ![]() $T$ is closed if
$T$ is closed if ![]() $dT=0$.
$dT=0$.
The exterior derivative defines a cochain complex structure on ![]() $(\mathcal {D}^\bullet (M))$, and Example 2.5 gives a morphism of cochain complexes
$(\mathcal {D}^\bullet (M))$, and Example 2.5 gives a morphism of cochain complexes
The previous morphism is, in fact, a quasi-isomorphism (i.e. it induces isomorphisms at the level of cohomology groups, see [Reference Griffiths and HarrisGH94, p. 382]).
The space ![]() $\mathcal {D}^k(M)$ is naturally a topological vector space when equipped with the weak topology: a sequence
$\mathcal {D}^k(M)$ is naturally a topological vector space when equipped with the weak topology: a sequence ![]() $T_n$ of degree
$T_n$ of degree ![]() $k$ currents converges weakly to a current
$k$ currents converges weakly to a current ![]() $T$ (which we write
$T$ (which we write ![]() $T_n \rightharpoonup T$) if
$T_n \rightharpoonup T$) if
for all ![]() $\beta \in \Omega _c^{n-k}(M)$.
$\beta \in \Omega _c^{n-k}(M)$.
Assume now that ![]() $M$ is a complex manifold of complex dimension
$M$ is a complex manifold of complex dimension ![]() $n$. Then the complex
$n$. Then the complex ![]() $\mathcal {D}^\bullet (M)$ admits a bigrading
$\mathcal {D}^\bullet (M)$ admits a bigrading
where ![]() $\mathcal {D}^{p,q}(M)$ is the topological dual of the complex vector space
$\mathcal {D}^{p,q}(M)$ is the topological dual of the complex vector space ![]() $\Omega _c^{n-p,n-q}(M)$.
$\Omega _c^{n-p,n-q}(M)$.
In particular, if ![]() $Z\subseteq M$ is a closed complex analytic subvariety of complex codimension
$Z\subseteq M$ is a closed complex analytic subvariety of complex codimension ![]() $k$, we can similarly define a closed integration current
$k$, we can similarly define a closed integration current ![]() $T_Z\in D^{k,k}(M)$ by integrating over (the smooth locus of)
$T_Z\in D^{k,k}(M)$ by integrating over (the smooth locus of) ![]() $Z$.
$Z$.
2.3 Homogeneous spaces, orientations, and volume forms
In this section, we introduce the notation that we use throughout the paper and recall some facts on volume forms on Lie groups.
Let ![]() $G$ denote a real algebraic semi-simple Lie group. Suppose we are given the following subgroups of
$G$ denote a real algebraic semi-simple Lie group. Suppose we are given the following subgroups of ![]() $G$:
$G$:
(i) a lattice
 $\Gamma$;
$\Gamma$;(ii) a semi-simple Lie subgroup
 $H$ without compact factor;
$H$ without compact factor;(iii) a compact subgroup
 $K$.
$K$.
Let ![]() $L$ be the intersection of
$L$ be the intersection of ![]() $K$ and
$K$ and ![]() $H$. This is a compact subgroup of
$H$. This is a compact subgroup of ![]() $H$. The group
$H$. The group ![]() $H$ acts on the right on the quotient
$H$ acts on the right on the quotient ![]() $\Gamma \backslash G$, and we are interested in the next section in equidistribution properties of orbits of this action and their projection to
$\Gamma \backslash G$, and we are interested in the next section in equidistribution properties of orbits of this action and their projection to ![]() $\Gamma \backslash G/K$.
$\Gamma \backslash G/K$.
Let ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\mathfrak {h}$,
$\mathfrak {h}$, ![]() $\mathfrak {k}$, and
$\mathfrak {k}$, and ![]() $\mathfrak {l}$ denote the Lie algebras of
$\mathfrak {l}$ denote the Lie algebras of ![]() $G$,
$G$, ![]() $H$,
$H$, ![]() $K$, and
$K$, and ![]() $L$, respectively. Up to taking subgroups of index two, we can assume that the adjoint actions of
$L$, respectively. Up to taking subgroups of index two, we can assume that the adjoint actions of ![]() $G$,
$G$, ![]() $H$,
$H$, ![]() $K$, and
$K$, and ![]() $L$ have determinant one. We then fix once and for all some orientation of
$L$ have determinant one. We then fix once and for all some orientation of ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\mathfrak {h}$,
$\mathfrak {h}$, ![]() $\mathfrak {k}$, and
$\mathfrak {k}$, and ![]() $\mathfrak {l}$ and orient accordingly the quotient spaces
$\mathfrak {l}$ and orient accordingly the quotient spaces ![]() $\mathfrak {g}/\mathfrak {k}$,
$\mathfrak {g}/\mathfrak {k}$, ![]() $\mathfrak {g}/\mathfrak {h}$,
$\mathfrak {g}/\mathfrak {h}$, ![]() $\mathfrak {g}/\mathfrak {l}$,
$\mathfrak {g}/\mathfrak {l}$, ![]() $\mathfrak {k}/\mathfrak {l}$, and
$\mathfrak {k}/\mathfrak {l}$, and ![]() $\mathfrak {h}/\mathfrak {l}$. Those orientations induce orientations on
$\mathfrak {h}/\mathfrak {l}$. Those orientations induce orientations on ![]() $G/K$,
$G/K$, ![]() $G/H$,
$G/H$, ![]() $G/L$,
$G/L$, ![]() $K/L$, and
$K/L$, and ![]() $H/L$, respectively.
$H/L$, respectively.
Recall that the Lie algebra ![]() $\mathfrak {g}$ carries a natural symmetric bilinear form called the Killing form, which is invariant under the adjoint action and non-degenerate because
$\mathfrak {g}$ carries a natural symmetric bilinear form called the Killing form, which is invariant under the adjoint action and non-degenerate because ![]() $G$ is semi-simple. Its restriction to
$G$ is semi-simple. Its restriction to ![]() $\mathfrak {h}$,
$\mathfrak {h}$, ![]() $\mathfrak {k}$, or
$\mathfrak {k}$, or ![]() $\mathfrak {l}$ is still non-degenerate. We denote by
$\mathfrak {l}$ is still non-degenerate. We denote by ![]() $\omega _G$,
$\omega _G$, ![]() $\omega _H$,
$\omega _H$, ![]() $\omega _K$, and
$\omega _K$, and ![]() $\omega _L$ the volume forms associated with the restricted Killing metric and the prescribed orientations on
$\omega _L$ the volume forms associated with the restricted Killing metric and the prescribed orientations on ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\mathfrak {h}$,
$\mathfrak {h}$, ![]() $\mathfrak {k}$, and
$\mathfrak {k}$, and ![]() $\mathfrak {l}$, respectively, as well as the induced bi-invariant volume forms on
$\mathfrak {l}$, respectively, as well as the induced bi-invariant volume forms on ![]() $G$,
$G$, ![]() $H$,
$H$, ![]() $K$, and
$K$, and ![]() $L$. Finally, we denote by
$L$. Finally, we denote by ![]() $\omega _{G/K}$,
$\omega _{G/K}$, ![]() $\omega _{G/H}$,
$\omega _{G/H}$, ![]() $\omega _{G/L}$,
$\omega _{G/L}$, ![]() $\omega _{K/L}$, and
$\omega _{K/L}$, and ![]() $\omega _{H/L}$ the invariant volume forms on the corresponding homogeneous spaces induced by
$\omega _{H/L}$ the invariant volume forms on the corresponding homogeneous spaces induced by ![]() $\omega _G$,
$\omega _G$, ![]() $\omega _H$,
$\omega _H$, ![]() $\omega _K$, and
$\omega _K$, and ![]() $\omega _L$.
$\omega _L$.
The volume forms ![]() $\omega _G$ and
$\omega _G$ and ![]() $\omega _{G/K}$ factor to volume forms on
$\omega _{G/K}$ factor to volume forms on ![]() $\Gamma \backslash G$ and
$\Gamma \backslash G$ and ![]() $\Gamma \backslash G/K$, respectively, and we define
$\Gamma \backslash G/K$, respectively, and we define
respectively. The compatibility of the volume forms gives the following identity:
Similarly, if ![]() $xH$ is a closed
$xH$ is a closed ![]() $H$-orbit in
$H$-orbit in ![]() $\Gamma \backslash G$, then
$\Gamma \backslash G$, then ![]() $\omega _H$,
$\omega _H$, ![]() $\omega _L$, and
$\omega _L$, and ![]() $\omega _{H/L}$ induce volume forms on
$\omega _{H/L}$ induce volume forms on ![]() $xH$,
$xH$, ![]() $L$, and
$L$, and ![]() $xH/L$. We denote by
$xH/L$. We denote by ![]() $\operatorname {Vol}(xH)$,
$\operatorname {Vol}(xH)$, ![]() $\operatorname {Vol}(L)$, and
$\operatorname {Vol}(L)$, and ![]() $\operatorname {Vol}(xH/L)$ their total masses, respectively, and we have the following identity:
$\operatorname {Vol}(xH/L)$ their total masses, respectively, and we have the following identity:
2.4 Equidistribution in terms of currents
In this section, we reformulate equidistribution results of sequences of ![]() $H$-orbits in terms of convergence of currents. As before, for all
$H$-orbits in terms of convergence of currents. As before, for all ![]() $n\in \mathbb {N}$, let
$n\in \mathbb {N}$, let ![]() $\mathcal {O}_n$ be a finite union of closed
$\mathcal {O}_n$ be a finite union of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. The starting point of our work is the remark that the equidistribution of a sequence
$\Gamma \backslash G$. The starting point of our work is the remark that the equidistribution of a sequence ![]() $\{\mathcal {O}_n\subset \Gamma \backslash G,n\in \mathbb {N}\}$ can be reformulated as an equidistribution of the currents of integration over
$\{\mathcal {O}_n\subset \Gamma \backslash G,n\in \mathbb {N}\}$ can be reformulated as an equidistribution of the currents of integration over ![]() $\mathcal {O}_n$.
$\mathcal {O}_n$.
To be more precise, let ![]() $p$ denote the projection from
$p$ denote the projection from ![]() $G/L$ to
$G/L$ to ![]() $G/H$ and
$G/H$ and ![]() $\pi$ the projection from
$\pi$ the projection from ![]() $G/L$ to
$G/L$ to ![]() $G/K$.
$G/K$.
Lemma 2.6 Assume that the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $\Gamma \backslash G$ and let
$\Gamma \backslash G$ and let ![]() $\widehat {T}_{\mathcal {O}_n/L}$ denote the integration current on
$\widehat {T}_{\mathcal {O}_n/L}$ denote the integration current on ![]() $\mathcal {O}_n/L \subset \Gamma \backslash G/L$. Then
$\mathcal {O}_n/L \subset \Gamma \backslash G/L$. Then
The form ![]() $p^*\omega _{G/H}$ can be seen as a transverse volume form to the foliation of
$p^*\omega _{G/H}$ can be seen as a transverse volume form to the foliation of ![]() $G/L$ by translates of
$G/L$ by translates of ![]() $H/L$. Note that, by applying the lemma to
$H/L$. Note that, by applying the lemma to ![]() $L= \{\mathbf {1}_G\}$, we obtain the following corollary.
$L= \{\mathbf {1}_G\}$, we obtain the following corollary.
Corollary 2.7 Assume that the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $\Gamma \backslash G$ and let
$\Gamma \backslash G$ and let ![]() $T_{\mathcal {O}_n}$ denote the integration current on
$T_{\mathcal {O}_n}$ denote the integration current on ![]() $\mathcal {O}_n$. Then
$\mathcal {O}_n$. Then
where ![]() $\widehat {p}$ is the projection from
$\widehat {p}$ is the projection from ![]() $G$ to
$G$ to ![]() $\Gamma \backslash G$.
$\Gamma \backslash G$.
Finally, one can push this equidistribution forward by the fibration map from ![]() $G/L$ to
$G/L$ to ![]() $G/K$. Recall that the map
$G/K$. Recall that the map ![]() $\pi$ induces a push-forward map
$\pi$ induces a push-forward map
which is, by definition, Poincaré dual to the pull-back map ![]() $\pi ^*$, i.e.
$\pi ^*$, i.e.
for all ![]() $\beta$ with compact support (for more details, see § 4.1 or [Reference Bott and TuBT82, p. 37]). We still denote by
$\beta$ with compact support (for more details, see § 4.1 or [Reference Bott and TuBT82, p. 37]). We still denote by ![]() $\pi$ and
$\pi$ and ![]() $\pi _*$ the factorization of those maps by the left action of
$\pi _*$ the factorization of those maps by the left action of ![]() $\Gamma$.
$\Gamma$.
Theorem 2.8 Assume the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ equidistributes in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ equidistributes in ![]() $\Gamma \backslash G$ and let
$\Gamma \backslash G$ and let ![]() $T_{\mathcal {O}_n/L}$ denote the integration current on
$T_{\mathcal {O}_n/L}$ denote the integration current on ![]() $\mathcal {O}_n/L \subset \Gamma \backslash G/K$. Then
$\mathcal {O}_n/L \subset \Gamma \backslash G/K$. Then
Proof. Let ![]() $\mathcal {H}$ denote the foliation of
$\mathcal {H}$ denote the foliation of ![]() $\Gamma \backslash G/L$ by the left translates of
$\Gamma \backslash G/L$ by the left translates of ![]() $H/L$ and
$H/L$ and ![]() $T\mathcal {H} \subset T(\Gamma \backslash G/L)$ the tangent distribution to this foliation. The volume form
$T\mathcal {H} \subset T(\Gamma \backslash G/L)$ the tangent distribution to this foliation. The volume form ![]() $\omega _{H/L}$ on
$\omega _{H/L}$ on ![]() $H/L$ defines a smooth section
$H/L$ defines a smooth section ![]() $\omega _{\mathcal {H}}$ of
$\omega _{\mathcal {H}}$ of ![]() $\Lambda ^{\max}T^*\mathcal {H}$.
$\Lambda ^{\max}T^*\mathcal {H}$.
Let ![]() $\alpha$ be a form of degree
$\alpha$ be a form of degree ![]() $\dim (G)-\dim (H)$ with compact support on
$\dim (G)-\dim (H)$ with compact support on ![]() $\Gamma \backslash G/L$, and let
$\Gamma \backslash G/L$, and let ![]() $f$ be the smooth function with compact support such that
$f$ be the smooth function with compact support such that ![]() $\alpha _{\vert T\mathcal {H}} = f \omega _{\mathcal {H}}$. The compatibility between the various volume forms gives
$\alpha _{\vert T\mathcal {H}} = f \omega _{\mathcal {H}}$. The compatibility between the various volume forms gives
Let ![]() $p_0$ denote the projection from
$p_0$ denote the projection from ![]() $\Gamma \backslash G$ to
$\Gamma \backslash G$ to ![]() $\Gamma \backslash G/L$. We have
$\Gamma \backslash G/L$. We have
 \begin{align*} \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)}\int_{\mathcal{O}_n/L} \alpha & = \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)}\int_{\mathcal{O}_n/L} f \omega_{\mathcal{H}}\\ & = \frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\int_{\mathcal{O}_n} f\circ p_0 \omega_H \\ &\quad\underset{n\to +\infty}{\longrightarrow} \frac{1}{\operatorname{Vol}(\Gamma \backslash G)}\int_{\Gamma \backslash G} f\circ p_0 \omega_G \end{align*}
\begin{align*} \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)}\int_{\mathcal{O}_n/L} \alpha & = \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)}\int_{\mathcal{O}_n/L} f \omega_{\mathcal{H}}\\ & = \frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\int_{\mathcal{O}_n} f\circ p_0 \omega_H \\ &\quad\underset{n\to +\infty}{\longrightarrow} \frac{1}{\operatorname{Vol}(\Gamma \backslash G)}\int_{\Gamma \backslash G} f\circ p_0 \omega_G \end{align*}
and
 \begin{align*} \frac{1}{\operatorname{Vol}(\Gamma \backslash G)}\int_{\Gamma \backslash G} f\circ p_0 \omega_G &= \frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)}\int_{\Gamma \backslash G/L} f \omega_{G/L}\\ &=\frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)}\int_{\Gamma \backslash G} \alpha \wedge p^*\omega_{G/H}. \end{align*}
\begin{align*} \frac{1}{\operatorname{Vol}(\Gamma \backslash G)}\int_{\Gamma \backslash G} f\circ p_0 \omega_G &= \frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)}\int_{\Gamma \backslash G/L} f \omega_{G/L}\\ &=\frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)}\int_{\Gamma \backslash G} \alpha \wedge p^*\omega_{G/H}. \end{align*}
This shows that ![]() $({1}/{\operatorname {Vol}(\mathcal {O}_n/L)})\widehat {T}_{\mathcal {O}_n/L}$ converges weakly to
$({1}/{\operatorname {Vol}(\mathcal {O}_n/L)})\widehat {T}_{\mathcal {O}_n/L}$ converges weakly to ![]() $({1}/{\operatorname {Vol}(\Gamma \backslash G/L)}) \omega _{G/H}$.
$({1}/{\operatorname {Vol}(\Gamma \backslash G/L)}) \omega _{G/H}$.
Proof of Theorem 2.8 We push forward the equidistribution of Lemma 2.6 to ![]() $\Gamma \backslash G/K$. Note that we have
$\Gamma \backslash G/K$. Note that we have ![]() $T_{\mathcal {O}_n/L} = \pi _* \widehat {T}_{\mathcal {O}_n/L}$.
$T_{\mathcal {O}_n/L} = \pi _* \widehat {T}_{\mathcal {O}_n/L}$.
Let ![]() $\alpha$ be a form of degree
$\alpha$ be a form of degree ![]() $\dim (H/L)$ with compact support on
$\dim (H/L)$ with compact support on ![]() $\Gamma \backslash G/K$. We then have
$\Gamma \backslash G/K$. We then have
 \begin{align*} \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)}\langle T_{\mathcal{O}_n/L}, \alpha\rangle & = \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)} \langle \widehat{T}_{\mathcal{O}_n/L}, \pi^*\alpha \rangle\\ &\to \frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)}\int_{\Gamma \backslash G/L} \pi^* \alpha \wedge p^* \omega_{G/H}\\ &= \frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)} \int_{\Gamma \backslash G/K} \alpha \wedge \pi_* p^* \omega_{G/H} \text{ (by definition of $\pi_*$).}\quad \end{align*}
\begin{align*} \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)}\langle T_{\mathcal{O}_n/L}, \alpha\rangle & = \frac{1}{\operatorname{Vol}(\mathcal{O}_n/L)} \langle \widehat{T}_{\mathcal{O}_n/L}, \pi^*\alpha \rangle\\ &\to \frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)}\int_{\Gamma \backslash G/L} \pi^* \alpha \wedge p^* \omega_{G/H}\\ &= \frac{1}{\operatorname{Vol}(\Gamma \backslash G/L)} \int_{\Gamma \backslash G/K} \alpha \wedge \pi_* p^* \omega_{G/H} \text{ (by definition of $\pi_*$).}\quad \end{align*}
For ![]() $n\in \mathbb {N}$, the integration current
$n\in \mathbb {N}$, the integration current ![]() $T_{\mathcal {O}_n/L}$ is closed because
$T_{\mathcal {O}_n/L}$ is closed because ![]() $\mathcal {O}_n/L$ has empty boundary. It thus has a well-defined cohomology class
$\mathcal {O}_n/L$ has empty boundary. It thus has a well-defined cohomology class ![]() $[\mathcal {O}_n/L]\in H^{d_H}(\Gamma \backslash G/K,\mathbb {R})$ where
$[\mathcal {O}_n/L]\in H^{d_H}(\Gamma \backslash G/K,\mathbb {R})$ where ![]() $d_H$ is the codimension of
$d_H$ is the codimension of ![]() $H/L$ in
$H/L$ in ![]() $G/K$.
$G/K$.
Corollary 2.9 Assume that the sequence ![]() $(\mathcal {O}_n)$ is equidistributed in
$(\mathcal {O}_n)$ is equidistributed in ![]() $\Gamma \backslash G$ and let
$\Gamma \backslash G$ and let ![]() $[\mathcal {O}_n/L]$ denote the corresponding cohomology class in
$[\mathcal {O}_n/L]$ denote the corresponding cohomology class in ![]() $H^{d_H}(\Gamma \backslash G/K,\mathbb {R})$. Then
$H^{d_H}(\Gamma \backslash G/K,\mathbb {R})$. Then
2.5 Ratner theory and its consequences
In this final section, we recall some equidistribution results à la Ratner of homogeneous orbits in locally homogeneous spaces. These results will be used when studying the refined Noether–Lefschetz locus in § 6.1.
We place ourselves in an arithmetic setting. Though this is not a requirement of Ratner theory, it is the source of its most remarkable consequences and will be sufficient for our applications.
We thus assume that we are given an inclusion ![]() $\mathbf {H}\subset \mathbf {G}$ of semi-simple algebraic groups over
$\mathbf {H}\subset \mathbf {G}$ of semi-simple algebraic groups over ![]() $\mathbb {Q}$ such that:
$\mathbb {Q}$ such that:
(i)
 $G$ is a subgroup of
$G$ is a subgroup of  $\mathbf {G}_\mathbb {R}$ containing
$\mathbf {G}_\mathbb {R}$ containing  $\mathbf {G}_\mathbb {R}^0$;
$\mathbf {G}_\mathbb {R}^0$;(ii)
 $H= G\cap \mathbf {H}_\mathbb {R}$;
$H= G\cap \mathbf {H}_\mathbb {R}$;(iii)
 $\Gamma$ is commensurable to
$\Gamma$ is commensurable to  $\rho ^{-1}(\operatorname {GL}(n,\mathbb {Z}))$, for some faithful representation
$\rho ^{-1}(\operatorname {GL}(n,\mathbb {Z}))$, for some faithful representation  $\phi : \mathbf {G} \to \operatorname {GL}(n)$ over
$\phi : \mathbf {G} \to \operatorname {GL}(n)$ over  $\mathbb {Q}$.Footnote 4
$\mathbb {Q}$.Footnote 4
By a lemma of Chevalley (see [Reference BenoistBen08, Proposition 4.6]), we can find a free ![]() $\mathbb {Z}$-module
$\mathbb {Z}$-module ![]() $\mathbf {V}_\mathbb {Z}$ and an embedding
$\mathbf {V}_\mathbb {Z}$ and an embedding ![]() $\mathbf {G}\hookrightarrow \operatorname {GL}(\mathbf {V}_\mathbb {Q})$ such that
$\mathbf {G}\hookrightarrow \operatorname {GL}(\mathbf {V}_\mathbb {Q})$ such that ![]() $\mathbf {H}$ is the stabilizer in
$\mathbf {H}$ is the stabilizer in ![]() $\mathbf {G}$ of a vector
$\mathbf {G}$ of a vector ![]() $v_0\in \mathbf {V}_\mathbb {Z}$. We can moreover assume that the
$v_0\in \mathbf {V}_\mathbb {Z}$. We can moreover assume that the ![]() $G$-orbit of
$G$-orbit of ![]() $v_0$ is Zariski closed and that
$v_0$ is Zariski closed and that ![]() $\Gamma$ preserves
$\Gamma$ preserves ![]() $\mathbf {V}_\mathbb {Z}$. For every
$\mathbf {V}_\mathbb {Z}$. For every ![]() $\lambda \in \mathbb {R}_{>0}$, we can now identify the homogeneous space
$\lambda \in \mathbb {R}_{>0}$, we can now identify the homogeneous space ![]() $G/H$ with the
$G/H$ with the ![]() $G$-orbit of
$G$-orbit of ![]() $\lambda v_0$ in
$\lambda v_0$ in ![]() $\mathbf {V}_\mathbb {R}$.
$\mathbf {V}_\mathbb {R}$.
The following classical result of homogeneous dynamics establishes the equivalence between closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$ and discrete
$\Gamma \backslash G$ and discrete ![]() $\Gamma$-orbits in
$\Gamma$-orbits in ![]() $G/H$.
$G/H$.
Lemma 2.10 Let ![]() $g$ be an element in
$g$ be an element in ![]() $G$, let
$G$, let ![]() $x$ be its projection to
$x$ be its projection to ![]() $\Gamma \backslash G$ and
$\Gamma \backslash G$ and ![]() $v = gv_0$ its projection to
$v = gv_0$ its projection to ![]() $Gv_0 = G/H$. Then the following are equivalent:
$Gv_0 = G/H$. Then the following are equivalent:
(i) the set
 $\Gamma g H$ is closed in
$\Gamma g H$ is closed in  $G$;
$G$;(ii) the right
 $H$-orbit of
$H$-orbit of  $x$ is closed in
$x$ is closed in  $\Gamma \backslash G$;
$\Gamma \backslash G$;(iii) the left
 $\Gamma$-orbit of
$\Gamma$-orbit of  $v$ is discrete in
$v$ is discrete in  $G/H$;
$G/H$;(iv) the group
 $\Gamma \cap gHg^{-1}$ is a lattice in
$\Gamma \cap gHg^{-1}$ is a lattice in  $gHg^{-1}$;
$gHg^{-1}$;(v) there exists
 $\lambda \in \mathbb {R}_{>0}$ such that
$\lambda \in \mathbb {R}_{>0}$ such that  $\lambda v \in V_\mathbb {Z}$.
$\lambda v \in V_\mathbb {Z}$.
Now let ![]() $V_n$ be a finite union of discrete
$V_n$ be a finite union of discrete ![]() $\Gamma$-orbits in
$\Gamma$-orbits in ![]() $G/H$ and let
$G/H$ and let ![]() $\mathcal {O}_n$ be the corresponding finite union of closed
$\mathcal {O}_n$ be the corresponding finite union of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. The volume form
$\Gamma \backslash G$. The volume form ![]() $\omega _H$ induces an
$\omega _H$ induces an ![]() $H$-invariant measure
$H$-invariant measure ![]() $\nu _n$ on
$\nu _n$ on ![]() $\Gamma \backslash G$, supported by
$\Gamma \backslash G$, supported by ![]() $\mathcal {O}_n$, whose total mass
$\mathcal {O}_n$, whose total mass ![]() $\operatorname {Vol}(\mathcal {O}_n)$ is finite.
$\operatorname {Vol}(\mathcal {O}_n)$ is finite.
Definition 2.11 We say that the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $\Gamma \backslash G$ if the sequence of probability measures
$\Gamma \backslash G$ if the sequence of probability measures
converges weakly to
We say that the sequence ![]() $(V_n)_{n\in \mathbb {N}}$ is equidistributed in
$(V_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $G/H$ if the discrete measure
$G/H$ if the discrete measure
 \[ \frac{1}{\operatorname{Vol}(\mathcal{O}_n)} \sum_{x\in V_n} \delta_x \]
\[ \frac{1}{\operatorname{Vol}(\mathcal{O}_n)} \sum_{x\in V_n} \delta_x \]
converges weakly to ![]() $\omega _{G/H}$.
$\omega _{G/H}$.
Recall the following classical lemma from [Reference Eskin and OhEO06b, Proposition 2.2].
Lemma 2.12 The sequence ![]() $(V_n)_{n\in \mathbb {N}}$ is equidistributed in
$(V_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $G/H$ if and only if the sequence
$G/H$ if and only if the sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $\Gamma \backslash G$.
$\Gamma \backslash G$.
In [Reference Eskin and OhEO06b], Eskin and Oh gave an equidistribution criterion for finite unions of closed orbits which relies on Ratner's groundbreaking work on unipotent dynamics as well as further developments by Mozes and Shah [Reference Mozes and ShahMS95] and Dani and Margulis [Reference Dani and MargulisDM93, DM93].
Let ![]() $\mathcal {O}_n = \bigcup _{i=1}^{l_n} x_{i,n} H$ be a finite union of closed
$\mathcal {O}_n = \bigcup _{i=1}^{l_n} x_{i,n} H$ be a finite union of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$ and let
$\Gamma \backslash G$ and let ![]() $V_n = \bigcup _{i=1}^{l_n} \Gamma v_{i,n}$ be the corresponding union of discrete
$V_n = \bigcup _{i=1}^{l_n} \Gamma v_{i,n}$ be the corresponding union of discrete ![]() $\Gamma$-orbits in
$\Gamma$-orbits in ![]() $G/H$.
$G/H$.
Definition 2.13 We say that the sequence ![]() $(\mathcal {O}_n)_{n\in N}$ has no loss of mass if for all compact subsets
$(\mathcal {O}_n)_{n\in N}$ has no loss of mass if for all compact subsets ![]() $C$ of
$C$ of ![]() $G/H$,
$G/H$,
 \[
\frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\Biggl(\sum_{\underset{x_{i,n}H\cap
C = \emptyset}{i}} \operatorname{Vol}(x_{i,n}H)\Biggr)\underset{n\to
+\infty}{\longrightarrow} 0. \]
\[
\frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\Biggl(\sum_{\underset{x_{i,n}H\cap
C = \emptyset}{i}} \operatorname{Vol}(x_{i,n}H)\Biggr)\underset{n\to
+\infty}{\longrightarrow} 0. \]
Definition 2.14 The sequence ![]() $(\mathcal {O}_n)$ is called focused if there exists
$(\mathcal {O}_n)$ is called focused if there exists ![]() $g\in G$ and a subgroup
$g\in G$ and a subgroup ![]() $H'$ of
$H'$ of ![]() $G$ containing
$G$ containing ![]() $gHg^{-1}$ and defined over
$gHg^{-1}$ and defined over ![]() $\mathbb {Q}$ such that
$\mathbb {Q}$ such that
 \[ \limsup_{n\to +\infty}
\frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\Biggl(\sum_{\underset{\Gamma
v_{i,n}\subset \Gamma H' g Z(H) v_0}{i}}
\operatorname{Vol}(x_{i,n}H)\Biggr)> 0.
\]
\[ \limsup_{n\to +\infty}
\frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\Biggl(\sum_{\underset{\Gamma
v_{i,n}\subset \Gamma H' g Z(H) v_0}{i}}
\operatorname{Vol}(x_{i,n}H)\Biggr)> 0.
\]
It is called non-focused otherwise.
Remark 2.15 Eskin and Oh's original definition of being non-focused combines both Definitions 2.13 and 2.14. It is more convenient to us to separate them, because we verify both conditions independently.
Theorem 2.16 [Reference Eskin and OhEO06b, Theorem 1.13]
Assume that ![]() $H$ is a semi-simple subgroup of
$H$ is a semi-simple subgroup of ![]() $G$ without compact factors. Then the sequence
$G$ without compact factors. Then the sequence ![]() $(V_n)_{n\in \mathbb {N}}$ is equidistributed in
$(V_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $G/H$ if and only if it is non-focused and has no loss of mass.
$G/H$ if and only if it is non-focused and has no loss of mass.
Note that a sequence of closed ![]() $H$-orbits of
$H$-orbits of ![]() $\Gamma \backslash G$ leaving every compact subset can only exist if
$\Gamma \backslash G$ leaving every compact subset can only exist if ![]() $H$ is contained in a proper parabolic subgroup of
$H$ is contained in a proper parabolic subgroup of ![]() $G$. We thus have the following proposition which results from Propositions 3.2 and 3.4 in [Reference Eskin and OhEO06b].
$G$. We thus have the following proposition which results from Propositions 3.2 and 3.4 in [Reference Eskin and OhEO06b].
Proposition 2.17 If ![]() $H$ is not contained in a proper parabolic subgroup of
$H$ is not contained in a proper parabolic subgroup of ![]() $G$, then any sequence of finite unions of closed
$G$, then any sequence of finite unions of closed ![]() $H$-orbits of
$H$-orbits of ![]() $\Gamma \backslash G$ has no loss of mass.
$\Gamma \backslash G$ has no loss of mass.
3. Equidistribution of intersection points
We consider as before a sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ of finite unions of closed
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ of finite unions of closed ![]() $H$-orbits of
$H$-orbits of ![]() $\Gamma \backslash G$ which is assumed to be equidistributed. In this section, we want to pass from the equidistribution in terms of currents to an equidistribution of the intersection points of
$\Gamma \backslash G$ which is assumed to be equidistributed. In this section, we want to pass from the equidistribution in terms of currents to an equidistribution of the intersection points of ![]() $\mathcal {O}_n$ with a subvariety of
$\mathcal {O}_n$ with a subvariety of ![]() $\Gamma \backslash G/K$ of dimension
$\Gamma \backslash G/K$ of dimension ![]() $d_H$. Though this kind of result can be expected to follow from Theorem 2.8, some work is needed to deal with the locus where this intersection is not transverse. This will require, in particular, a finiteness result for maps defined in an o-minimal structure.
$d_H$. Though this kind of result can be expected to follow from Theorem 2.8, some work is needed to deal with the locus where this intersection is not transverse. This will require, in particular, a finiteness result for maps defined in an o-minimal structure.
3.1 Moderate geometry of locally symmetric spaces
We recall in this section notions from o-minimal geometry in the context of locally symmetric spaces following [Reference Bakker, Klingler and TsimermanBKT20] and the structure of definable maps. For a general introduction to o-minimal structures, we refer to [Reference van den DriesvdD98].
A structure ![]() $\mathcal {S}$ on
$\mathcal {S}$ on ![]() $\mathbb {R}$ expanding the real field
$\mathbb {R}$ expanding the real field ![]() $\mathbb {R}$ is by definition a collection
$\mathbb {R}$ is by definition a collection ![]() $(\mathcal {S}_n)_{n\in \mathbb {N}^\times }$ where each
$(\mathcal {S}_n)_{n\in \mathbb {N}^\times }$ where each ![]() $\mathcal {S}_n$ is a set of subsets of
$\mathcal {S}_n$ is a set of subsets of ![]() $\mathbb {R}^n$, called the definable sets, which is a Boolean subalgebra of the subsets of
$\mathbb {R}^n$, called the definable sets, which is a Boolean subalgebra of the subsets of ![]() $\mathbb {R}^n$ containing all the algebraic subsets and which satisfy the following properties:
$\mathbb {R}^n$ containing all the algebraic subsets and which satisfy the following properties:
(i) if
 $A\in \mathcal {S}_n$,
$A\in \mathcal {S}_n$,  $B\in \mathcal {S}_m$, then
$B\in \mathcal {S}_m$, then  $A\times B\in \mathcal {S}_{n+m}$;
$A\times B\in \mathcal {S}_{n+m}$;(ii) if
 $p:\mathbb {R}^{n+1}\rightarrow \mathbb {R}^n$ is the projection on the first
$p:\mathbb {R}^{n+1}\rightarrow \mathbb {R}^n$ is the projection on the first  $n$-coordinates,
$n$-coordinates,  $A\in \mathcal {S}_{n+1}$, then
$A\in \mathcal {S}_{n+1}$, then  $p(A)\in \mathcal {S}_n$.
$p(A)\in \mathcal {S}_n$.
The structure is called o-minimal Footnote 5 if any element of ![]() $\mathcal {S}_1$ is a finite union of points and intervals. Given an o-minimal structure, one can define the following notions:
$\mathcal {S}_1$ is a finite union of points and intervals. Given an o-minimal structure, one can define the following notions:
(i) a map
 $f:A\rightarrow B$ between two definable sets is definable if its graph
$f:A\rightarrow B$ between two definable sets is definable if its graph  $\Gamma _f\subset A\times B$ is definable;
$\Gamma _f\subset A\times B$ is definable;(ii) a
 $\mathcal {S}$-definable manifold is a manifold having a finite atlas of charts
$\mathcal {S}$-definable manifold is a manifold having a finite atlas of charts  $(\phi _i:U_i\rightarrow \mathbb {R}^n)_{i\in I}$ such that the intersections
$(\phi _i:U_i\rightarrow \mathbb {R}^n)_{i\in I}$ such that the intersections  $\phi _i(U_i\cap U_j)\subset \mathbb {R}^n$ are definable and the change of coordinates maps
$\phi _i(U_i\cap U_j)\subset \mathbb {R}^n$ are definable and the change of coordinates maps  $\phi _i\circ \phi _j^{-1}:\phi _j(U_i\cap U_j)\rightarrow \phi _i(U_i\cap U_j)$ are
$\phi _i\circ \phi _j^{-1}:\phi _j(U_i\cap U_j)\rightarrow \phi _i(U_i\cap U_j)$ are  $\mathcal {S}$-definable maps.
$\mathcal {S}$-definable maps.
Intuitively, definable manifolds in an o-minimal structure have reasonable geometry locally and at infinity, complex algebraic varieties being an example of definable manifolds. The first example of an o-minimal structure is that given by semi-algebraic subsets denoted by ![]() $\mathbb {R}_{\rm alg}$. More examples of o-minimal structures have been studied during recent years and the ones relevant to Hodge theory are:
$\mathbb {R}_{\rm alg}$. More examples of o-minimal structures have been studied during recent years and the ones relevant to Hodge theory are:
(i)
 $\mathbb {R}_{\rm an}$, the smallest o-minimal structure expanding
$\mathbb {R}_{\rm an}$, the smallest o-minimal structure expanding  $\mathbb {R}_{\rm alg}$ and for which restricted analytic functions are definable (see [Reference GabrièlovGab68]);
$\mathbb {R}_{\rm alg}$ and for which restricted analytic functions are definable (see [Reference GabrièlovGab68]);(ii)
 $\mathbb {R}_{\rm exp}$, the smallest o-minimal structure expanding
$\mathbb {R}_{\rm exp}$, the smallest o-minimal structure expanding  $\mathbb {R}_{\rm alg}$ and for which the real exponential map is definable [Reference WilkieWil96];
$\mathbb {R}_{\rm alg}$ and for which the real exponential map is definable [Reference WilkieWil96];(iii)
 $\mathbb {R}_{\rm an,exp}$, the smallest o-minimal structure expanding the two previous structures [Reference van den Dries and MillervdDM94, Reference van den Dries and MillervdDM96].
$\mathbb {R}_{\rm an,exp}$, the smallest o-minimal structure expanding the two previous structures [Reference van den Dries and MillervdDM94, Reference van den Dries and MillervdDM96].
One of the main theorems of [Reference Bakker, Klingler and TsimermanBKT20, Theorem 1.1] asserts that locally symmetric spaces can be endowed with a semi-algebraic structure which is compatible in ![]() $\mathbb {R}_{\rm an}$ with the analytic structure on the Borel–Serre compactification, see [Reference Bakker, Klingler and TsimermanBKT20] for more details. More precisely, let
$\mathbb {R}_{\rm an}$ with the analytic structure on the Borel–Serre compactification, see [Reference Bakker, Klingler and TsimermanBKT20] for more details. More precisely, let ![]() $G$ be a real connected semi-simple group which has a
$G$ be a real connected semi-simple group which has a ![]() $\mathbb {Q}$-structure,
$\mathbb {Q}$-structure, ![]() $\Gamma$ a torsion-free arithmetic subgroup of
$\Gamma$ a torsion-free arithmetic subgroup of ![]() $G$ and
$G$ and ![]() $K\subset G$ a compact sub-group.
$K\subset G$ a compact sub-group.
Theorem 3.1 [Reference Bakker, Klingler and TsimermanBKT20, Theorem 1.1]
The quotients ![]() $G/K$,
$G/K$, ![]() $\Gamma \backslash G/K$ have
$\Gamma \backslash G/K$ have ![]() $\mathbb {R}_{\rm alg}$ structures such that:
$\mathbb {R}_{\rm alg}$ structures such that:
(i)
 $G\rightarrow G/K$ is definable in
$G\rightarrow G/K$ is definable in  $\mathbb {R}_{\rm alg}$;
$\mathbb {R}_{\rm alg}$;(ii) there exists a definable fundamental domain
 $\mathcal {F}\subset G/K$ for the action of
$\mathcal {F}\subset G/K$ for the action of  $\Gamma$ such that
$\Gamma$ such that  $\mathcal {F}\rightarrow \Gamma \backslash G/K$ is definable in
$\mathcal {F}\rightarrow \Gamma \backslash G/K$ is definable in  $\mathbb {R}_{\rm alg}$.
$\mathbb {R}_{\rm alg}$.
Moreover, this structure is functorial in the triple ![]() $(G,K,\Gamma )$.
$(G,K,\Gamma )$.
One last ingredient we need from o-minimal geometry is the structure of definable maps: a definable map ![]() $f:M\rightarrow N$ between definable sets has a definable trivialization if there exists a pair
$f:M\rightarrow N$ between definable sets has a definable trivialization if there exists a pair ![]() $(F,\lambda )$ where
$(F,\lambda )$ where ![]() $F$ is a definable set and
$F$ is a definable set and ![]() $\lambda : M\rightarrow F$ is a definable map which induces a definable homeomorphism
$\lambda : M\rightarrow F$ is a definable map which induces a definable homeomorphism ![]() $M\rightarrow F\times N$ compatible with maps to
$M\rightarrow F\times N$ compatible with maps to ![]() $N$. The following theorem is from [Reference van den DriesvdD98, Chapter 9, Theorem 1.2].
$N$. The following theorem is from [Reference van den DriesvdD98, Chapter 9, Theorem 1.2].
Theorem 3.2 Let ![]() $f:M\rightarrow N$ be a continuous definable map between definable sets in an o-minimal structure
$f:M\rightarrow N$ be a continuous definable map between definable sets in an o-minimal structure ![]() $\mathcal {S}$. Then there exists a finite partition
$\mathcal {S}$. Then there exists a finite partition ![]() $(N_i)_i$ by definable subsets of
$(N_i)_i$ by definable subsets of ![]() $N$ such that
$N$ such that ![]() $f:f^{-1}(N_i)\rightarrow N_i$ is definably trivial.
$f:f^{-1}(N_i)\rightarrow N_i$ is definably trivial.
An easy corollary is that the number of connected components of the fibers of a definable map is finite and uniformly bounded.
3.2 Counting intersection points
In this section, we explain our conventions for counting points of intersection of varieties mapping to the quotient ![]() $\Gamma \backslash G/K$ with closed
$\Gamma \backslash G/K$ with closed ![]() $H$-orbits. We adopt the same notation as in § 2.3 to which we refer. From now on,
$H$-orbits. We adopt the same notation as in § 2.3 to which we refer. From now on, ![]() $\mathcal {S}$ will be a fixed o-minimal structure which extends
$\mathcal {S}$ will be a fixed o-minimal structure which extends ![]() $\mathbb {R}_{\rm alg}$.
$\mathbb {R}_{\rm alg}$.
Let ![]() $S\subset \Gamma \backslash G/K$ be a definable real analytic subvariety of dimension
$S\subset \Gamma \backslash G/K$ be a definable real analytic subvariety of dimension ![]() $d_H = \dim (G/K)-\dim (H/L)$, and assume that the smooth locus of
$d_H = \dim (G/K)-\dim (H/L)$, and assume that the smooth locus of ![]() $S$ is oriented. Let
$S$ is oriented. Let ![]() $\mathcal {O}$ be a finite union of closed
$\mathcal {O}$ be a finite union of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. Recall that we denote by
$\Gamma \backslash G$. Recall that we denote by ![]() $\mathcal {O}/L$ its projection to
$\mathcal {O}/L$ its projection to ![]() $\Gamma \backslash G/L$ and by
$\Gamma \backslash G/L$ and by ![]() $\pi (\mathcal {O}/L)$ its projection to
$\pi (\mathcal {O}/L)$ its projection to ![]() $\Gamma \backslash G/K$.
$\Gamma \backslash G/K$.
In general, ![]() $\pi _{\vert \mathcal {O}/L}$ is not an embedding, which is why it is more convenient to count intersection at the level of
$\pi _{\vert \mathcal {O}/L}$ is not an embedding, which is why it is more convenient to count intersection at the level of ![]() $\Gamma \backslash G/L$, where
$\Gamma \backslash G/L$, where ![]() $\mathcal {O}/L$ is a finite union of closed leaves of the foliation
$\mathcal {O}/L$ is a finite union of closed leaves of the foliation ![]() $\mathcal {H}$ introduced in § 2.4.
$\mathcal {H}$ introduced in § 2.4.
Let ![]() $(\Gamma \backslash G/L)_S$ be the preimage of
$(\Gamma \backslash G/L)_S$ be the preimage of ![]() $S$ by the fibration
$S$ by the fibration ![]() $\pi : \Gamma \backslash G/L\rightarrow \Gamma \backslash G/K$. By assumption on
$\pi : \Gamma \backslash G/L\rightarrow \Gamma \backslash G/K$. By assumption on ![]() $S$,
$S$, ![]() $(\Gamma \backslash G/L)_S$ and
$(\Gamma \backslash G/L)_S$ and ![]() $\mathcal {O}/L$ have complementary dimension in
$\mathcal {O}/L$ have complementary dimension in ![]() $\Gamma \backslash G/L$. A point
$\Gamma \backslash G/L$. A point ![]() $y\in (\Gamma \backslash G/L)_S \cap \mathcal {O}/L$ is a transverse intersection point if
$y\in (\Gamma \backslash G/L)_S \cap \mathcal {O}/L$ is a transverse intersection point if ![]() $(\Gamma \backslash G/L)_S$ is smooth at
$(\Gamma \backslash G/L)_S$ is smooth at ![]() $y$ (equivalently, if
$y$ (equivalently, if ![]() $S$ is smooth at
$S$ is smooth at ![]() $\pi (y)$) and
$\pi (y)$) and
For ![]() $y\in (\Gamma \backslash G/L)_S \cap \mathcal {O}$, we set
$y\in (\Gamma \backslash G/L)_S \cap \mathcal {O}$, we set ![]() $\epsilon (y) = 0$ if
$\epsilon (y) = 0$ if ![]() $y$ is not a transverse intersection point, and
$y$ is not a transverse intersection point, and ![]() $\epsilon (y) =1$ if
$\epsilon (y) =1$ if ![]() $y$ is a transverse intersection point such that the direct sum (3.2.1) is compatible with orientations, and
$y$ is a transverse intersection point such that the direct sum (3.2.1) is compatible with orientations, and ![]() $\epsilon (y) = -1$ otherwise.
$\epsilon (y) = -1$ otherwise.
We have the following distribution on ![]() $(\Gamma \backslash G/L)_S$ given by summing over transverse intersection points:
$(\Gamma \backslash G/L)_S$ given by summing over transverse intersection points:
Note that, because ![]() $(\Gamma \backslash G/L)_S\cap \mathcal {O}/L$ is definable, it has a finite number of connected components. Moreover, components of dimension at least one consist only of non-transverse intersections points, for which
$(\Gamma \backslash G/L)_S\cap \mathcal {O}/L$ is definable, it has a finite number of connected components. Moreover, components of dimension at least one consist only of non-transverse intersections points, for which ![]() $\epsilon (y) = 0$. Hence,
$\epsilon (y) = 0$. Hence, ![]() $\widehat {T}_\mathcal {O}^S$ is a finite signed measure. We can finally state the following definition.
$\widehat {T}_\mathcal {O}^S$ is a finite signed measure. We can finally state the following definition.
Definition 3.3 The transverse intersection measure between ![]() $S$ and
$S$ and ![]() $\mathcal {O}/L$ is the signed measure
$\mathcal {O}/L$ is the signed measure
Informally, ![]() $T^S_{\mathcal {O}}$, counts the transverse intersection points of
$T^S_{\mathcal {O}}$, counts the transverse intersection points of ![]() $S$ and
$S$ and ![]() $\pi (\mathcal {O}/L)$, with a multiplicity corresponding to the (signed) number of branches of
$\pi (\mathcal {O}/L)$, with a multiplicity corresponding to the (signed) number of branches of ![]() $\pi (\mathcal {O}/L)$ meeting
$\pi (\mathcal {O}/L)$ meeting ![]() $S$ at a smooth point
$S$ at a smooth point ![]() $x$. The asymptotic behavior on
$x$. The asymptotic behavior on ![]() $S$ of the distributions
$S$ of the distributions ![]() $T_{\mathcal {O}_n}^S$ for an equidistributing sequence
$T_{\mathcal {O}_n}^S$ for an equidistributing sequence ![]() $\mathcal {O}_n$ is discussed in the next section. In particular, we prove that they are equidistributed with respect to the form
$\mathcal {O}_n$ is discussed in the next section. In particular, we prove that they are equidistributed with respect to the form ![]() $\pi _*p^*\omega _{G/H}$.
$\pi _*p^*\omega _{G/H}$.
Remark 3.4 In general, the intersection ![]() $S\cap \pi (\mathcal {O}/L)$ could have zero-dimensional components which are not transverse because they are not reduced or are not smooth points of
$S\cap \pi (\mathcal {O}/L)$ could have zero-dimensional components which are not transverse because they are not reduced or are not smooth points of ![]() $S$. We do not take them into account in
$S$. We do not take them into account in ![]() $T_\mathcal {O}^S$, but we show in the next section that they are negligible from the equidistribution point of view.
$T_\mathcal {O}^S$, but we show in the next section that they are negligible from the equidistribution point of view.
Remark 3.5 Working in the setting of a moderate geometry allows us to avoid topological pathologies which do not arise in the applications we intend to give and makes it possible at the same time to make statements in a more general setting.
3.3 Equidistribution of intersection points
We keep the notation from the previous section, namely, ![]() $G$ is a semi-simple
$G$ is a semi-simple ![]() $\mathbb {Q}$-group,
$\mathbb {Q}$-group, ![]() $\Gamma \subset G$ is a torsion-free arithmetic subgroup, and
$\Gamma \subset G$ is a torsion-free arithmetic subgroup, and ![]() $H\subset G$ is a semi-simple subgroup without compact factor. Let
$H\subset G$ is a semi-simple subgroup without compact factor. Let ![]() $\mathcal {D}=G/K$ where
$\mathcal {D}=G/K$ where ![]() $K\subset G$ is a compact subgroup and
$K\subset G$ is a compact subgroup and ![]() $L=K\cap H$. Let
$L=K\cap H$. Let ![]() $d_H$ be as before the codimension of
$d_H$ be as before the codimension of ![]() $H/L$ in
$H/L$ in ![]() $\mathcal {D}$. Let
$\mathcal {D}$. Let ![]() $S$ be an analytic subvariety of
$S$ be an analytic subvariety of ![]() $\Gamma \backslash \mathcal {D}$ of dimension
$\Gamma \backslash \mathcal {D}$ of dimension ![]() $d_H$ and consider an equidistributing sequence
$d_H$ and consider an equidistributing sequence ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ of finite unions of closed
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ of finite unions of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. In this section, we refine Theorem 2.8 into an equidistribution theorem for the measures
$\Gamma \backslash G$. In this section, we refine Theorem 2.8 into an equidistribution theorem for the measures ![]() $T^S_{\mathcal {O}_n}$ introduced in the previous paragraph, which will imply Theorem 1.1.
$T^S_{\mathcal {O}_n}$ introduced in the previous paragraph, which will imply Theorem 1.1.
Theorem 3.6 Let ![]() $S$ be an analytic subspace of
$S$ be an analytic subspace of ![]() $\Gamma \backslash \mathcal {D}$ of dimension
$\Gamma \backslash \mathcal {D}$ of dimension ![]() $d_H$ and let
$d_H$ and let ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ be an equidistributing sequence of finite unions of closed
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ be an equidistributing sequence of finite unions of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. Then
$\Gamma \backslash G$. Then
Proof. Recall that it is enough to prove the weak convergence on every open subset of a covering of ![]() $S$ by Proposition 2.1. We can thus restrict ourselves to an open relatively compact definable subset
$S$ by Proposition 2.1. We can thus restrict ourselves to an open relatively compact definable subset ![]() $\Omega \subset S$ that lifts to
$\Omega \subset S$ that lifts to ![]() $\mathcal {D}$. We still denote this lift by
$\mathcal {D}$. We still denote this lift by ![]() $\Omega$. We want to prove the equidistribution of the transverse intersection of
$\Omega$. We want to prove the equidistribution of the transverse intersection of ![]() $\Omega$ with
$\Omega$ with ![]() $\pi (p^{-1}(V_n))$, where
$\pi (p^{-1}(V_n))$, where ![]() $V_n$ is the finite union of discrete
$V_n$ is the finite union of discrete ![]() $\Gamma$-orbits in
$\Gamma$-orbits in ![]() $G/H$ such that
$G/H$ such that ![]() $\mathcal {O}_n = \Gamma \backslash \pi ^{-1}(V_n)$.
$\mathcal {O}_n = \Gamma \backslash \pi ^{-1}(V_n)$.
Denote by ![]() $(G/L)_\Omega$ the preimage of
$(G/L)_\Omega$ the preimage of ![]() $\Omega$ by
$\Omega$ by ![]() $\pi$, and consider the following open subsets of
$\pi$, and consider the following open subsets of ![]() $(G/L)_\Omega$:
$(G/L)_\Omega$:
(i) the domain
 $U_{\rm smooth}$ where
$U_{\rm smooth}$ where  $(G/L)_\Omega$ is smooth;
$(G/L)_\Omega$ is smooth;(ii) the domain
 $U_{\rm sub}$ where
$U_{\rm sub}$ where  $(G/L)_\Omega$ is smooth and
$(G/L)_\Omega$ is smooth and  $p_{\vert \Omega }$ is a submersion (hence, a local diffeomorphism by equality of the dimensions).
$p_{\vert \Omega }$ is a submersion (hence, a local diffeomorphism by equality of the dimensions).
By definition, the distribution ![]() $\widehat {T}_{\mathcal {O}_n}^\Omega$ is supported by
$\widehat {T}_{\mathcal {O}_n}^\Omega$ is supported by ![]() $U_{\rm sub}$. We first prove that
$U_{\rm sub}$. We first prove that ![]() $({1}/{\operatorname {Vol}(\mathcal {O}_n)}) \widehat {T}_{\mathcal {O}_n}^\Omega$ converges weakly to
$({1}/{\operatorname {Vol}(\mathcal {O}_n)}) \widehat {T}_{\mathcal {O}_n}^\Omega$ converges weakly to ![]() $p^*\omega _{G/H}$ on
$p^*\omega _{G/H}$ on ![]() $U_{\rm sub}$, then extend the weak convergence successively to
$U_{\rm sub}$, then extend the weak convergence successively to ![]() $U_{\rm smooth}$ and
$U_{\rm smooth}$ and ![]() $(G/L)_\Omega$ using Proposition 2.2. After pushing forward by
$(G/L)_\Omega$ using Proposition 2.2. After pushing forward by ![]() $\pi$, we get the desired result.
$\pi$, we get the desired result.
To prove the weak convergence on ![]() $U_{\rm sub}$, it is enough to prove it on every open relatively compact subset
$U_{\rm sub}$, it is enough to prove it on every open relatively compact subset ![]() $U'$ of
$U'$ of ![]() $U_{\rm sub}$ such that
$U_{\rm sub}$ such that ![]() $p_{\vert U'}$ is a diffeomorphism onto its image (because those open sets cover
$p_{\vert U'}$ is a diffeomorphism onto its image (because those open sets cover ![]() $U_{\rm sub}$). Thus, let
$U_{\rm sub}$). Thus, let ![]() $f$ be a continuous function with compact support on such
$f$ be a continuous function with compact support on such ![]() $U'$. Let
$U'$. Let ![]() $\epsilon (U')$ be
$\epsilon (U')$ be ![]() $1$ if
$1$ if ![]() $p_{\vert U'}$ preserves orientation and
$p_{\vert U'}$ preserves orientation and ![]() $-1$ otherwise. Then
$-1$ otherwise. Then
 \begin{align*} \frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\widehat{T}_{\mathcal{O}_n}^{\Omega}(f) &= \frac{\epsilon(U')}{\operatorname{Vol}(\mathcal{O}_n)} \sum_{x\in V_n\cap p(U')} f\circ p^{-1}(x)\\ &\quad \underset{n\to+\infty}{\longrightarrow} \epsilon(U') \int_{p(U')} f\circ p^{-1}(x) \omega_{G/H}(x)= \int_{U'} f p^*\omega_{G/H} \end{align*}
\begin{align*} \frac{1}{\operatorname{Vol}(\mathcal{O}_n)}\widehat{T}_{\mathcal{O}_n}^{\Omega}(f) &= \frac{\epsilon(U')}{\operatorname{Vol}(\mathcal{O}_n)} \sum_{x\in V_n\cap p(U')} f\circ p^{-1}(x)\\ &\quad \underset{n\to+\infty}{\longrightarrow} \epsilon(U') \int_{p(U')} f\circ p^{-1}(x) \omega_{G/H}(x)= \int_{U'} f p^*\omega_{G/H} \end{align*}
because ![]() $V_n$ is equidistributed in
$V_n$ is equidistributed in ![]() $G/H$.
$G/H$.
This shows the weak convergence of ![]() $({1}/{\operatorname {Vol}(\mathcal {O}_n)})\widehat {T}_{\mathcal {O}_n}^{\Omega }$ on every
$({1}/{\operatorname {Vol}(\mathcal {O}_n)})\widehat {T}_{\mathcal {O}_n}^{\Omega }$ on every ![]() $U'$, hence on
$U'$, hence on ![]() $U_{\rm sub}$.
$U_{\rm sub}$.
Let us now extend the weak convergence to ![]() $(G/L)_\Omega$. As the projection map
$(G/L)_\Omega$. As the projection map ![]() $p_{\vert (G/L)_\Omega }: (G/L)_\Omega \to G/H$ is definable in the o-minimal structure
$p_{\vert (G/L)_\Omega }: (G/L)_\Omega \to G/H$ is definable in the o-minimal structure ![]() $\mathbb {R}_{\rm an,exp}$, it follows from Theorem 3.2 that the number of connected components of its fibers is uniformly bounded by some number
$\mathbb {R}_{\rm an,exp}$, it follows from Theorem 3.2 that the number of connected components of its fibers is uniformly bounded by some number ![]() $N$.
$N$.
First, let ![]() $C$ be a compact subset of
$C$ be a compact subset of ![]() $U_{\rm smooth}\setminus U_{\rm sub}$. Then, by Sard's lemma,
$U_{\rm smooth}\setminus U_{\rm sub}$. Then, by Sard's lemma, ![]() $p(C)$ has measure
$p(C)$ has measure ![]() $0$. Hence, for every
$0$. Hence, for every ![]() $\epsilon >0$, there exists an open neighborhood
$\epsilon >0$, there exists an open neighborhood ![]() $U'$ of
$U'$ of ![]() $C$ in
$C$ in ![]() $U_{\rm smooth}$ such that
$U_{\rm smooth}$ such that
As for all ![]() $x\in p(U')\cap V_n$ the set
$x\in p(U')\cap V_n$ the set ![]() $p^{-1}(x)\cap U'$ has at most
$p^{-1}(x)\cap U'$ has at most ![]() $N$ isolated points, we get that
$N$ isolated points, we get that
hence
We conclude that ![]() $({1}/{\operatorname {Vol}(\mathcal {O}_n)})\widehat {T}_{\mathcal {O}_n}^{\Omega }$ converges weakly on
$({1}/{\operatorname {Vol}(\mathcal {O}_n)})\widehat {T}_{\mathcal {O}_n}^{\Omega }$ converges weakly on ![]() $U_{\rm smooth}$ by Proposition 2.2.
$U_{\rm smooth}$ by Proposition 2.2.
Finally, the complement of ![]() $U_{\rm smooth}$ in
$U_{\rm smooth}$ in ![]() $(G/L)_\Omega$ is the singular locus, which has dimension less than
$(G/L)_\Omega$ is the singular locus, which has dimension less than ![]() $d_H$. As
$d_H$. As ![]() $p$ is definable, its image has measure zero, and one can reproduce the previous argument to show that
$p$ is definable, its image has measure zero, and one can reproduce the previous argument to show that ![]() $({1}/{\operatorname {Vol}(\mathcal {O}_n)})\widehat {T}_{\mathcal {O}_n}^{\Omega }$ converges weakly to
$({1}/{\operatorname {Vol}(\mathcal {O}_n)})\widehat {T}_{\mathcal {O}_n}^{\Omega }$ converges weakly to ![]() $p^*\omega _{G/H}$ on
$p^*\omega _{G/H}$ on ![]() $(G/L)_\Omega$.
$(G/L)_\Omega$.
In the previous theorem, we chose to restrict to ![]() $\dim (S)= d_H$ for simplicity. We indicate briefly without proof how these statements should be adapted when
$\dim (S)= d_H$ for simplicity. We indicate briefly without proof how these statements should be adapted when ![]() $\dim (S)> d_H$: we define the transverse intersection current
$\dim (S)> d_H$: we define the transverse intersection current ![]() $T_S^{\mathcal {O}_n}$ as the integration current over the transverse intersection locus of
$T_S^{\mathcal {O}_n}$ as the integration current over the transverse intersection locus of ![]() $S\cap \mathcal {O}_n$ with the sign normalizations as in § 3.2. Intersecting further with submanifolds of dimension
$S\cap \mathcal {O}_n$ with the sign normalizations as in § 3.2. Intersecting further with submanifolds of dimension ![]() $d_H$ and applying our theorem, one would obtain the convergence of these intersection currents (after normalization) to the current
$d_H$ and applying our theorem, one would obtain the convergence of these intersection currents (after normalization) to the current ![]() ${\pi _*p^*\omega _{G/H}}_{\vert S}$. We thus get the following theorem.
${\pi _*p^*\omega _{G/H}}_{\vert S}$. We thus get the following theorem.
Theorem 3.7 Let ![]() $S$ be an analytic subspace of dimension
$S$ be an analytic subspace of dimension ![]() $d\geq d_H$ and let
$d\geq d_H$ and let ![]() $(\mathcal {O}_n)_{n\in \mathbb {N}}$ be an equidistributing sequence of finite unions of closed
$(\mathcal {O}_n)_{n\in \mathbb {N}}$ be an equidistributing sequence of finite unions of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. Then for every
$\Gamma \backslash G$. Then for every ![]() $\beta \in \Omega _{c}^{d-d_H}(S)$, we have
$\beta \in \Omega _{c}^{d-d_H}(S)$, we have
4. The pull–push form
In the equidistribution Theorem 2.8 and Corollary 2.9, we see appearing the pull–push form ![]() $\pi _*p^*\omega _{G/H}$. This form was already studied by the second author with entirely different motivations [Reference TholozanTho15], whereas the first author proved, in the particular case of
$\pi _*p^*\omega _{G/H}$. This form was already studied by the second author with entirely different motivations [Reference TholozanTho15], whereas the first author proved, in the particular case of ![]() $G= \operatorname {SO}(2,q)$,
$G= \operatorname {SO}(2,q)$, ![]() $H= \operatorname {SO}(2,q-1)$, and
$H= \operatorname {SO}(2,q-1)$, and ![]() $K= \mathrm S(O(2)\times O(q))$, that this form is the
$K= \mathrm S(O(2)\times O(q))$, that this form is the ![]() $G$-invariant Kähler form on
$G$-invariant Kähler form on ![]() $G/K$.
$G/K$.
Here we introduce some tools to better characterize this form, most of which were already presented in [Reference TholozanTho15].
4.1 Push-forward of forms
Let us first recall without any proof the construction of the push-forward of a form ![]() $\alpha$ under a smooth fibration
$\alpha$ under a smooth fibration ![]() $\pi : M\to B$ with compact oriented fibers. This construction can be found for instance in [Reference Bott and TuBT82, p. 37].
$\pi : M\to B$ with compact oriented fibers. This construction can be found for instance in [Reference Bott and TuBT82, p. 37].
Let ![]() $r$ be the dimension of the fibers of
$r$ be the dimension of the fibers of ![]() $\pi$. Let
$\pi$. Let ![]() $x$ be a point in
$x$ be a point in ![]() $B$ and denote by
$B$ and denote by ![]() $F$ the fiber of
$F$ the fiber of ![]() $\pi$ over
$\pi$ over ![]() $x$. Choose
$x$. Choose ![]() $\omega$ a volume form on
$\omega$ a volume form on ![]() $F$ compatible with the orientation of the fiber, and let
$F$ compatible with the orientation of the fiber, and let
be the multivector such that ![]() $\omega (X) = 1$.
$\omega (X) = 1$.
Now let ![]() $\alpha$ be a smooth
$\alpha$ be a smooth ![]() $p$-form on
$p$-form on ![]() $M$. The contraction
$M$. The contraction ![]() $\iota _X\alpha$ is a
$\iota _X\alpha$ is a ![]() $(p-r)$ form with kernel
$(p-r)$ form with kernel ![]() $TF$, which can thus be seen as a section of
$TF$, which can thus be seen as a section of ![]() $\Lambda ^{p-r}(NF^\vee )$, where
$\Lambda ^{p-r}(NF^\vee )$, where ![]() $NF = TM/TF$ is the normal bundle to
$NF = TM/TF$ is the normal bundle to ![]() $F$ and
$F$ and ![]() $NF^\vee = \{\varphi \in T^*M \mid \varphi _{\vert TF} = 0\}$ is its dual.
$NF^\vee = \{\varphi \in T^*M \mid \varphi _{\vert TF} = 0\}$ is its dual.
Finally, the differential of ![]() $\pi$ along the fiber
$\pi$ along the fiber ![]() $F$ induces an isomorphism
$F$ induces an isomorphism ![]() $NF \simeq F\times T_xB$ and therefore
$NF \simeq F\times T_xB$ and therefore ![]() $\Lambda ^{p-r}(NF^\vee ) = \Lambda ^{p-r}(T_xB^\vee )$. With these identifications, we can now state the following definition.
$\Lambda ^{p-r}(NF^\vee ) = \Lambda ^{p-r}(T_xB^\vee )$. With these identifications, we can now state the following definition.
Definition 4.1 The push-forward of the form ![]() $\alpha$ is the
$\alpha$ is the ![]() $(p-r)$-form on
$(p-r)$-form on ![]() $B$ given at
$B$ given at ![]() $x$ by
$x$ by
Let ![]() $p+q$ be the dimension of
$p+q$ be the dimension of ![]() $M$. Then we have the following result.
$M$. Then we have the following result.
Proposition 4.2 The form ![]() $\pi _*\alpha$ is the unique
$\pi _*\alpha$ is the unique ![]() $(p-r)$ form on
$(p-r)$ form on ![]() $B$ such that for any
$B$ such that for any ![]() $q$-form
$q$-form ![]() $\beta$ on
$\beta$ on ![]() $B$ with compact support,
$B$ with compact support,
Moreover, the push-forward operation commutes with the exterior derivative. In particular, the push-forward of a closed form is closed.
4.2 A formula for the pull–push form
Let us now apply the previous general considerations in order to give a formula for the pull–push form ![]() $\pi _*p^*\omega _{G/H}$ at the Lie algebra level.
$\pi _*p^*\omega _{G/H}$ at the Lie algebra level.
Let ![]() $G/H$ be a
$G/H$ be a ![]() $G$-homogeneous space and
$G$-homogeneous space and ![]() $o$ denote the basepoint of
$o$ denote the basepoint of ![]() $G/H$ (that is, the projection of the unit element of
$G/H$ (that is, the projection of the unit element of ![]() $G$). Then the tangent space
$G$). Then the tangent space ![]() $T_o G/H$ with the induced linear action of
$T_o G/H$ with the induced linear action of ![]() $H$ identifies canonically with
$H$ identifies canonically with ![]() $\mathfrak {g}/\mathfrak {h}$ endowed with the adjoint action of
$\mathfrak {g}/\mathfrak {h}$ endowed with the adjoint action of ![]() $H$. This identification induces an isomorphism between the differential algebra
$H$. This identification induces an isomorphism between the differential algebra ![]() $\Omega ^\bullet (G/H, \mathbb {C})^G$ of smooth
$\Omega ^\bullet (G/H, \mathbb {C})^G$ of smooth ![]() $G$-invariant forms on
$G$-invariant forms on ![]() $G/H$ with complex coefficients and the differential algebra
$G/H$ with complex coefficients and the differential algebra ![]() $\Lambda ^\bullet ((\mathfrak {g}/\mathfrak {h})_\mathbb {C}^\vee )^H$ of
$\Lambda ^\bullet ((\mathfrak {g}/\mathfrak {h})_\mathbb {C}^\vee )^H$ of ![]() $H$-invariant exterior forms on
$H$-invariant exterior forms on ![]() $\mathfrak {g}/\mathfrak {h}$, with derivative given by
$\mathfrak {g}/\mathfrak {h}$, with derivative given by
for ![]() $\alpha \in \Lambda ^k((\mathfrak {g}/\mathfrak {h})_\mathbb {C}^\vee )^H$ and
$\alpha \in \Lambda ^k((\mathfrak {g}/\mathfrak {h})_\mathbb {C}^\vee )^H$ and ![]() $x_1,\ldots,x_{k+1}\in \mathfrak {g}/\mathfrak {h}$.
$x_1,\ldots,x_{k+1}\in \mathfrak {g}/\mathfrak {h}$.
Let us now come back to the setting of the previous section, where ![]() $H$ is a semi-simple subgroup of
$H$ is a semi-simple subgroup of ![]() $G$,
$G$, ![]() $K$ a compact subgroup of
$K$ a compact subgroup of ![]() $G$, and
$G$, and ![]() $L=G/H$. At the Lie algebra level, the pull-back homomorphism
$L=G/H$. At the Lie algebra level, the pull-back homomorphism ![]() $p^*$ (respectively,
$p^*$ (respectively, ![]() $\pi ^*$) identifies exterior forms on
$\pi ^*$) identifies exterior forms on ![]() $\mathfrak {g}/\mathfrak {h}$ (respectively,
$\mathfrak {g}/\mathfrak {h}$ (respectively, ![]() $\mathfrak {g}/\mathfrak {k}$) to those exterior forms on
$\mathfrak {g}/\mathfrak {k}$) to those exterior forms on ![]() $\mathfrak {g}/\mathfrak {l}$ having
$\mathfrak {g}/\mathfrak {l}$ having ![]() $\mathfrak {h}/\mathfrak {l}$ (respectively,
$\mathfrak {h}/\mathfrak {l}$ (respectively, ![]() $\mathfrak {k}/\mathfrak {l}$) in their kernel.
$\mathfrak {k}/\mathfrak {l}$) in their kernel.
Reinterpreting Definition 4.1 for ![]() $G$-invariant forms on
$G$-invariant forms on ![]() $G/L$, we obtain the following result.
$G/L$, we obtain the following result.
Proposition 4.3 Let ![]() $\alpha$ be a
$\alpha$ be a ![]() $G$-invariant form on
$G$-invariant form on ![]() $G/L$. Then the form
$G/L$. Then the form ![]() $\pi _*\alpha$ on
$\pi _*\alpha$ on ![]() $G/K$ is
$G/K$ is ![]() $G$-invariant and corresponds on
$G$-invariant and corresponds on ![]() $\mathfrak {g}/\mathfrak {k}$ to the
$\mathfrak {g}/\mathfrak {k}$ to the ![]() $\operatorname {Ad}_K$-invariant form
$\operatorname {Ad}_K$-invariant form
where ![]() $u \in \Lambda ^{\max} (\mathfrak {k}/\mathfrak {l})$ is such that
$u \in \Lambda ^{\max} (\mathfrak {k}/\mathfrak {l})$ is such that ![]() $\omega _{K/L}(u) = 1$.
$\omega _{K/L}(u) = 1$.
Remark 4.4 As ![]() $\mathfrak {k}/\mathfrak {l}$ and
$\mathfrak {k}/\mathfrak {l}$ and ![]() $\mathfrak {h}/\mathfrak {l}$ are both
$\mathfrak {h}/\mathfrak {l}$ are both ![]() $\operatorname {Ad}_L$-invariant, the form
$\operatorname {Ad}_L$-invariant, the form ![]() $\iota _u \alpha$ is
$\iota _u \alpha$ is ![]() $L$-invariant and its kernel contains
$L$-invariant and its kernel contains ![]() $\mathfrak {k}/\mathfrak {l}$. Therefore, its pull-back by
$\mathfrak {k}/\mathfrak {l}$. Therefore, its pull-back by ![]() $\operatorname {Ad}_k$ only depends on the class of
$\operatorname {Ad}_k$ only depends on the class of ![]() $k$ in
$k$ in ![]() $K/L$ so that the integral makes sense. Moreover, the resulting form is obviously
$K/L$ so that the integral makes sense. Moreover, the resulting form is obviously ![]() $K$-invariant and has
$K$-invariant and has ![]() $\mathfrak {k}/\mathfrak {l}$ in its kernel, so that is does identify with a
$\mathfrak {k}/\mathfrak {l}$ in its kernel, so that is does identify with a ![]() $K$-invariant form on
$K$-invariant form on ![]() $\mathfrak {g}/\mathfrak {k}$.
$\mathfrak {g}/\mathfrak {k}$.
Corollary 4.5 Let ![]() $(\alpha _1\ldots, \alpha _{p_r})$ be an oriented orthonormal basis of
$(\alpha _1\ldots, \alpha _{p_r})$ be an oriented orthonormal basis of ![]() $\{\phi \in (\mathfrak {g}/\mathfrak {k})^\vee \mid \phi _{\vert \mathfrak {h}/\mathfrak {l}} = 0\}$. Then there exists a positive constant
$\{\phi \in (\mathfrak {g}/\mathfrak {k})^\vee \mid \phi _{\vert \mathfrak {h}/\mathfrak {l}} = 0\}$. Then there exists a positive constant ![]() $\lambda$ such that
$\lambda$ such that
If, moreover, ![]() $\mathfrak {k}/\mathfrak {l}$ is orthogonal to
$\mathfrak {k}/\mathfrak {l}$ is orthogonal to ![]() $\mathfrak {h}/\mathfrak {l}$ in
$\mathfrak {h}/\mathfrak {l}$ in ![]() $\mathfrak {g}/\mathfrak {l}$, then
$\mathfrak {g}/\mathfrak {l}$, then ![]() $\lambda = 1$.
$\lambda = 1$.
Proof of Proposition 4.3 The ![]() $G$-invariance of
$G$-invariance of ![]() $\pi _*\alpha$ easily follows from Proposition 4.2, so we only need to compute
$\pi _*\alpha$ easily follows from Proposition 4.2, so we only need to compute ![]() $\pi _*\alpha$ at the basepoint of
$\pi _*\alpha$ at the basepoint of ![]() $G/K$.
$G/K$.
Let ![]() $o$ denote the basepoint of
$o$ denote the basepoint of ![]() $G/L$ and
$G/L$ and ![]() $v_1,\ldots, v_{p-r}$ be
$v_1,\ldots, v_{p-r}$ be ![]() $p-r$ vectors in
$p-r$ vectors in ![]() $T_o G/L = \mathfrak {g}/\mathfrak {l}$. Let
$T_o G/L = \mathfrak {g}/\mathfrak {l}$. Let ![]() $k$ be an element of
$k$ be an element of ![]() $K$. At the point
$K$. At the point ![]() $k\cdot o$, we have
$k\cdot o$, we have
by left invariance of ![]() $\iota _u \alpha$.
$\iota _u \alpha$.
Now, the differential of ![]() $\pi$ maps a vector
$\pi$ maps a vector ![]() $k\cdot v \in T_{k\cdot o}G/L$ to the vector
$k\cdot v \in T_{k\cdot o}G/L$ to the vector ![]() $\operatorname {Ad}_{k}(v) \in T_{\pi (o)} G/K = \mathfrak {g}/\mathfrak {k}$. Applying Definition 4.1 to
$\operatorname {Ad}_{k}(v) \in T_{\pi (o)} G/K = \mathfrak {g}/\mathfrak {k}$. Applying Definition 4.1 to ![]() $\pi _*\alpha$ gives the required formula.
$\pi _*\alpha$ gives the required formula.
Proof of Corollary 4.5 Complete ![]() $(\alpha _1,\ldots, \alpha _{p-r})$ into an orthonormal basis
$(\alpha _1,\ldots, \alpha _{p-r})$ into an orthonormal basis ![]() $(\beta _1,\ldots, \beta _r, \alpha _1, \ldots, \alpha _{p-r})$ of
$(\beta _1,\ldots, \beta _r, \alpha _1, \ldots, \alpha _{p-r})$ of ![]() $\{\phi \in (\mathfrak {g}/\mathfrak {l})^* \mid \phi _{\vert \mathfrak {h}/\mathfrak {l}}=0\}$. We then have
$\{\phi \in (\mathfrak {g}/\mathfrak {l})^* \mid \phi _{\vert \mathfrak {h}/\mathfrak {l}}=0\}$. We then have
 \[ p^*\omega_{G/H} = \bigwedge_{i=1}^r \beta_i \wedge \bigwedge_{i=1}^{p-r} \alpha_i, \]
\[ p^*\omega_{G/H} = \bigwedge_{i=1}^r \beta_i \wedge \bigwedge_{i=1}^{p-r} \alpha_i, \]
hence
 \[ \iota_up^*\omega_{G/H} = \lambda \bigwedge_{i=1}^{p-r} \alpha_i, \]
\[ \iota_up^*\omega_{G/H} = \lambda \bigwedge_{i=1}^{p-r} \alpha_i, \]
where ![]() $\lambda = \bigwedge _{i=1}^r \beta _i(u)$, because all the
$\lambda = \bigwedge _{i=1}^r \beta _i(u)$, because all the ![]() $\alpha _i$ vanish on
$\alpha _i$ vanish on ![]() $\mathfrak {k}/\mathfrak {l}$.
$\mathfrak {k}/\mathfrak {l}$.
If, furthermore, ![]() $\mathfrak {k}/\mathfrak {l}$ is orthogonal to
$\mathfrak {k}/\mathfrak {l}$ is orthogonal to ![]() $\mathfrak {h}/\mathfrak {l}$, then
$\mathfrak {h}/\mathfrak {l}$, then ![]() $(\beta _1, \ldots, \beta _r)$ can be chosen as an orthonormal basis of
$(\beta _1, \ldots, \beta _r)$ can be chosen as an orthonormal basis of ![]() $(\mathfrak {k}/\mathfrak {l})^\vee$, so that
$(\mathfrak {k}/\mathfrak {l})^\vee$, so that ![]() $\lambda =1$.
$\lambda =1$.
Proposition 4.3 now concludes the proof.
In practice, using this integral formula to compute the pull–push form quickly leads to rather involved computations. In [Reference TholozanTho15], the second author used this formula to give a sufficient vanishing criterion: if there exists ![]() $k\in K$ such that
$k\in K$ such that ![]() $\operatorname {Ad}_k$ preserves
$\operatorname {Ad}_k$ preserves ![]() $\mathfrak {h}/\mathfrak {l}$ and reverses its orientation, then
$\mathfrak {h}/\mathfrak {l}$ and reverses its orientation, then ![]() ${\operatorname {Ad}_k}_* (\iota _u \alpha ) = - \iota _u \alpha$, and Proposition 4.3 shows that
${\operatorname {Ad}_k}_* (\iota _u \alpha ) = - \iota _u \alpha$, and Proposition 4.3 shows that ![]() $\pi _*p^*\omega _{G/H}$ vanishes.
$\pi _*p^*\omega _{G/H}$ vanishes.
In terms of our equidistribution result, this vanishing means that the positive and negative part of the intersection measure cancel out asymptotically, because a ‘random’ translate of ![]() $H/L$ in
$H/L$ in ![]() $G/K$ can intersect a submanifold
$G/K$ can intersect a submanifold ![]() $S$ with two opposite equiprobable orientations.
$S$ with two opposite equiprobable orientations.
In contrast, we can prove the following non-vanishing criterion.
Corollary 4.6 If ![]() $G/K$ has a
$G/K$ has a ![]() $G$-invariant complex structure such that
$G$-invariant complex structure such that ![]() $H/L$ is a complex submanifold, then
$H/L$ is a complex submanifold, then ![]() $\pi _*p^*\omega _{G/H}$ does not vanish.
$\pi _*p^*\omega _{G/H}$ does not vanish.
Proof. Let ![]() $\alpha _1,\ldots, \alpha _{({p-r})/{2}}$ be a complex basis of
$\alpha _1,\ldots, \alpha _{({p-r})/{2}}$ be a complex basis of ![]() $\{\phi \in (\mathfrak {g}/\mathfrak {k})^\vee \mid \phi _{\vert \mathfrak {h}/\mathfrak {l}}=0\}$. Then
$\{\phi \in (\mathfrak {g}/\mathfrak {k})^\vee \mid \phi _{\vert \mathfrak {h}/\mathfrak {l}}=0\}$. Then ![]() $\iota _u p^*\omega _{G/H}$ is proportional to
$\iota _u p^*\omega _{G/H}$ is proportional to
 \[ \bigwedge_{i=1}^{({p-r})/{2}}
\alpha_i\wedge \bar\alpha_i,\]
\[ \bigwedge_{i=1}^{({p-r})/{2}}
\alpha_i\wedge \bar\alpha_i,\]
which is non-negative on every complex subspace of dimension ![]() $({p-r})/{2}$. By invariance of the complex structure, the same holds for
$({p-r})/{2}$. By invariance of the complex structure, the same holds for
 \[
{\operatorname{Ad}_k}^*\Biggl(\bigwedge_{i=1}^{({p-r})/{2}}
\alpha_i\wedge \bar\alpha_i\Biggr). \]
\[
{\operatorname{Ad}_k}^*\Biggl(\bigwedge_{i=1}^{({p-r})/{2}}
\alpha_i\wedge \bar\alpha_i\Biggr). \]
Finally, ![]() $\bigwedge _{i=1}^{({p-r})/{2}} \alpha _i\wedge \bar \alpha _i$ is positive on a complex complement of
$\bigwedge _{i=1}^{({p-r})/{2}} \alpha _i\wedge \bar \alpha _i$ is positive on a complex complement of ![]() $\mathfrak {h}/\mathfrak {l}$, and so is
$\mathfrak {h}/\mathfrak {l}$, and so is
 \[ \int_{k\in K/L}
{\operatorname{Ad}_k}^*\Biggl(\bigwedge_{i=1}^{({p-r})/{2}}
\alpha_i\wedge \bar\alpha_i\Biggr)
\omega_{K/L}.\quad \]
\[ \int_{k\in K/L}
{\operatorname{Ad}_k}^*\Biggl(\bigwedge_{i=1}^{({p-r})/{2}}
\alpha_i\wedge \bar\alpha_i\Biggr)
\omega_{K/L}.\quad \]
4.3 Compact duality
In [Reference TholozanTho15], the second author investigated further the pull–push form in the case where ![]() $G/K$ and
$G/K$ and ![]() $H/L$ are symmetric spaces. There, he proved that
$H/L$ are symmetric spaces. There, he proved that ![]() $\pi _*p^*\omega _{G/H}$ is in some sense ‘Poincaré dual’ to the inclusion
$\pi _*p^*\omega _{G/H}$ is in some sense ‘Poincaré dual’ to the inclusion ![]() $H/L\hookrightarrow G/K$, a statement which is made precise by passing to the compact dual of the symmetric space. As cohomology classes of compact symmetric spaces are represented by a unique invariant form, this argument completely characterizes the pull–push forms and provides an efficient way to compute it in practice. The goal of this section is to extend these results to more general compact subgroups
$H/L\hookrightarrow G/K$, a statement which is made precise by passing to the compact dual of the symmetric space. As cohomology classes of compact symmetric spaces are represented by a unique invariant form, this argument completely characterizes the pull–push forms and provides an efficient way to compute it in practice. The goal of this section is to extend these results to more general compact subgroups ![]() $K\subset G$.
$K\subset G$.
Recall that a Cartan involution of ![]() $G$ is an involutive automorphism whose fixed subgroup is a maximal compact subgroup. All the Cartan involutions of
$G$ is an involutive automorphism whose fixed subgroup is a maximal compact subgroup. All the Cartan involutions of ![]() $G$ are conjugated, and every compact subgroup of
$G$ are conjugated, and every compact subgroup of ![]() $G$ is fixed by a Cartan involution.
$G$ is fixed by a Cartan involution.
In this section, we make the assumption (verified in all the examples we consider in this paper) that there exists a Cartan involution ![]() $\theta$ of
$\theta$ of ![]() $G$ fixing
$G$ fixing ![]() $K$ and preserving
$K$ and preserving ![]() $H$. We denote by
$H$. We denote by ![]() $G^\theta$ and
$G^\theta$ and ![]() $H^\theta$ the compact subgroups of
$H^\theta$ the compact subgroups of ![]() $G$ and
$G$ and ![]() $H$ fixed by
$H$ fixed by ![]() $\theta$. The Lie algebras
$\theta$. The Lie algebras ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\mathfrak {h}$ decompose respectively as
$\mathfrak {h}$ decompose respectively as
and
We now introduce the dual Lie algebras
and
These are the Lie algebras of compact real forms ![]() $G_U$ and
$G_U$ and ![]() $H_U$ of
$H_U$ of ![]() $G_\mathbb {C}$ and
$G_\mathbb {C}$ and ![]() $H_\mathbb {C}$, respectively, called the compact duals of
$H_\mathbb {C}$, respectively, called the compact duals of ![]() $G$ and
$G$ and ![]() $H$.
$H$.
From ![]() $G_U$ and
$G_U$ and ![]() $H_U$, one can define compact duals to the homogeneous spaces
$H_U$, one can define compact duals to the homogeneous spaces ![]() $G/H$,
$G/H$, ![]() $G/L$, and
$G/L$, and ![]() $G/K$, given by
$G/K$, given by ![]() $G_U/H_U$,
$G_U/H_U$, ![]() $G_U/L$, and
$G_U/L$, and ![]() $G_U/K$, respectively. The various inclusions between these groups give the following commutative diagram.
$G_U/K$, respectively. The various inclusions between these groups give the following commutative diagram.

Now, the inclusion of ![]() $G/H$ into
$G/H$ into ![]() $G_\mathbb {C}/H_\mathbb {C}$ induces an isomorphism of differential algebras
$G_\mathbb {C}/H_\mathbb {C}$ induces an isomorphism of differential algebras
where ![]() $\Lambda ^\bullet _\mathbb {C}$ and
$\Lambda ^\bullet _\mathbb {C}$ and ![]() $\Omega ^\bullet _\mathbb {C}$ denote the complex of
$\Omega ^\bullet _\mathbb {C}$ denote the complex of ![]() $\mathbb {C}$-multilinear forms. The same holds for all the inclusions in the above diagram. In other words, the differential algebra of real invariant forms on a homogeneous space and its compact dual are two distinct real forms of the same complex differential algebra.
$\mathbb {C}$-multilinear forms. The same holds for all the inclusions in the above diagram. In other words, the differential algebra of real invariant forms on a homogeneous space and its compact dual are two distinct real forms of the same complex differential algebra.
Proposition 4.7 We have the following commutative diagram of differential complexes.

Proof. The only non-trivial point is that ![]() $\pi _*$ and
$\pi _*$ and ![]() ${\pi _U}_*$ are identified as maps from
${\pi _U}_*$ are identified as maps from ![]() $\Omega _\mathbb {C}^\bullet (G_\mathbb {C}/L_\mathbb {C})^{G_\mathbb {C}}$ to
$\Omega _\mathbb {C}^\bullet (G_\mathbb {C}/L_\mathbb {C})^{G_\mathbb {C}}$ to ![]() $\Omega _\mathbb {C}^\bullet (G_\mathbb {C}/K_\mathbb {C})^{G_\mathbb {C}}$. However, this readily follows from Proposition 4.3 because, at the Lie algebra level, both maps are given by the contraction with
$\Omega _\mathbb {C}^\bullet (G_\mathbb {C}/K_\mathbb {C})^{G_\mathbb {C}}$. However, this readily follows from Proposition 4.3 because, at the Lie algebra level, both maps are given by the contraction with ![]() $u$ followed by averaging under the adjoint action of
$u$ followed by averaging under the adjoint action of ![]() $K$.
$K$.
Now, ![]() $\omega _{G/H}$ and
$\omega _{G/H}$ and ![]() $\omega _{G_U/H_U}$ are both generators of
$\omega _{G_U/H_U}$ are both generators of ![]() $\Lambda ^{\max}_\mathbb {C}(\mathfrak {g}_\mathbb {C}/\mathfrak {h}_\mathbb {C})$, so they are complex multiples one of the other. More precisely, we can identify
$\Lambda ^{\max}_\mathbb {C}(\mathfrak {g}_\mathbb {C}/\mathfrak {h}_\mathbb {C})$, so they are complex multiples one of the other. More precisely, we can identify
with
via the morphism
and normalize ![]() $\omega _{G_U/H_U}$ so that
$\omega _{G_U/H_U}$ so that
With this normalization, we have the following equality in ![]() $\Lambda ^{\max}_\mathbb {C}(\mathfrak {g}_\mathbb {C}/\mathfrak {h}_\mathbb {C})$
$\Lambda ^{\max}_\mathbb {C}(\mathfrak {g}_\mathbb {C}/\mathfrak {h}_\mathbb {C})$
Finally, applying Proposition 4.7, we conclude as follows.
Corollary 4.8 The following equality holds in ![]() $\Lambda ^\bullet _\mathbb {C}(G_\mathbb {C}/K_\mathbb {C})^{K_\mathbb {C}}$:
$\Lambda ^\bullet _\mathbb {C}(G_\mathbb {C}/K_\mathbb {C})^{K_\mathbb {C}}$:
What we gained by switching to the compact dual space ![]() $G_U/K$ is that we can now talk about the cohomology class of the pull–push form. The following theorem was proven in [Reference TholozanTho15] under the assumption that
$G_U/K$ is that we can now talk about the cohomology class of the pull–push form. The following theorem was proven in [Reference TholozanTho15] under the assumption that ![]() $K=G^\theta$, but the proof easily adapts to our more general context.
$K=G^\theta$, but the proof easily adapts to our more general context.
Lemma 4.9 The de Rham cohomology class of the pull–push form ![]() $({1}/{\operatorname {Vol}(G_U/H_U)}) {\pi _U}_* p_U^*\omega _{G_U/H_U}$ is Poincaré dual to the homology class of
$({1}/{\operatorname {Vol}(G_U/H_U)}) {\pi _U}_* p_U^*\omega _{G_U/H_U}$ is Poincaré dual to the homology class of ![]() $H_U/L \subset G_U/K$; that is, for every closed form
$H_U/L \subset G_U/K$; that is, for every closed form ![]() $\beta$ on
$\beta$ on ![]() $G_U/K$ of degree
$G_U/K$ of degree ![]() $\dim (H_U/L)$, we have
$\dim (H_U/L)$, we have
Proof. This is essentially formal. Denote by ![]() $\iota _1$ and
$\iota _1$ and ![]() $\iota _2$ the inclusions of
$\iota _2$ the inclusions of ![]() $H_U/L$ in
$H_U/L$ in ![]() $G_U/L$ and
$G_U/L$ and ![]() $G_U/K$, respectively, so that we have
$G_U/K$, respectively, so that we have ![]() $\iota _2 = \pi _U\circ \iota _1$ and
$\iota _2 = \pi _U\circ \iota _1$ and ![]() $\iota _1(H_U/L) = p_U^{-1}(o)$, where
$\iota _1(H_U/L) = p_U^{-1}(o)$, where ![]() $o$ is the basepoint of
$o$ is the basepoint of ![]() $G_U/H_U$.
$G_U/H_U$.
Now, the form ![]() $({1}/{\operatorname {Vol}(G_U/H_U)})\omega _{G_U/H_U}$ is Poincaré dual to
$({1}/{\operatorname {Vol}(G_U/H_U)})\omega _{G_U/H_U}$ is Poincaré dual to ![]() $[o]$ in
$[o]$ in ![]() $\mathrm H_{dR}^\bullet (G_U/H_U,\mathbb {R})$, so its pull-back under
$\mathrm H_{dR}^\bullet (G_U/H_U,\mathbb {R})$, so its pull-back under ![]() $p_U$ is Poincaré dual to
$p_U$ is Poincaré dual to ![]() $[{p}_{U}^{-1}(o)] = \iota _{1*}[H_U/L]$. Finally, let
$[{p}_{U}^{-1}(o)] = \iota _{1*}[H_U/L]$. Finally, let ![]() $\beta$ be a closed form of degree
$\beta$ be a closed form of degree ![]() $\dim (H_U/L)$ on
$\dim (H_U/L)$ on ![]() $G_U/K$. We then have
$G_U/K$. We then have
 \begin{align*} \int_{H_U/L} \iota_2^* \beta &= \int_{\iota_1(H_U/L)} \pi_U^*\beta \\ &= \int_{G_U/L}p_U^*\omega_{G_U/H_U}\wedge \pi_U^*\beta\\ &= \int_{G_U/K} {\pi_U}_*p_U^* \omega_{G_U/H_U} \wedge \beta.\quad \end{align*}
\begin{align*} \int_{H_U/L} \iota_2^* \beta &= \int_{\iota_1(H_U/L)} \pi_U^*\beta \\ &= \int_{G_U/L}p_U^*\omega_{G_U/H_U}\wedge \pi_U^*\beta\\ &= \int_{G_U/K} {\pi_U}_*p_U^* \omega_{G_U/H_U} \wedge \beta.\quad \end{align*}
4.3.1 The symmetric case
When ![]() $K= G^\theta$ is a maximal compact subgroup of
$K= G^\theta$ is a maximal compact subgroup of ![]() $G$, a theorem of Cartan [Reference CartanCart30] states that all
$G$, a theorem of Cartan [Reference CartanCart30] states that all ![]() $G$-invariant forms on
$G$-invariant forms on ![]() $G/K$ are closed. Hence, the exterior derivative is trivial on
$G/K$ are closed. Hence, the exterior derivative is trivial on ![]() $\Omega ^\bullet (G/K)^G$ and we have isomorphisms:
$\Omega ^\bullet (G/K)^G$ and we have isomorphisms:
In other words, a ![]() $G$-invariant form on
$G$-invariant form on ![]() $G/K$ is completely characterized by the cohomology class of the corresponding form on
$G/K$ is completely characterized by the cohomology class of the corresponding form on ![]() $G_U/K$.
$G_U/K$.
This property does not hold for more general homogeneous spaces. In the next section we show however that it remains true on Mumford–Tate domains when restricting to a variation of Hodge structure.
5. Invariant forms on period domains
In this section, we introduce Mumford–Tate domains, Hodge loci, and invariant forms on period domains. Then we relate pull–push forms to Chern classes of Hodge bundles. Finally, we compute it in various cases of interest.
5.1 Variations of Hodge structure and their period domains
Let us first recall some definitions of Hodge theory, merely to fix notation.
Let ![]() $V$ be a free
$V$ be a free ![]() $\mathbb {Z}$-module of finite rank
$\mathbb {Z}$-module of finite rank ![]() $d\in \mathbb {N}$ endowed with a bilinear form
$d\in \mathbb {N}$ endowed with a bilinear form ![]() $B: V\times V \to \mathbb {Z}$. Given a field
$B: V\times V \to \mathbb {Z}$. Given a field ![]() $\mathbb {K}$, we write
$\mathbb {K}$, we write ![]() $V_\mathbb {K}= V\otimes _\mathbb {Z}\mathbb {K}$ and still denote by
$V_\mathbb {K}= V\otimes _\mathbb {Z}\mathbb {K}$ and still denote by ![]() $B$ the natural
$B$ the natural ![]() $\mathbb {K}$-bilinear extension of
$\mathbb {K}$-bilinear extension of ![]() $B$ to
$B$ to ![]() $V_\mathbb {K}$.
$V_\mathbb {K}$.
A Hodge structure of weight ![]() $k$ on
$k$ on ![]() $V$ polarized by
$V$ polarized by ![]() $B$ is the data of a filtration of complex vector spaces
$B$ is the data of a filtration of complex vector spaces
such that for all ![]() $0\leq p\leq k$:
$0\leq p\leq k$:
(i)
 $V_\mathbb {C}=F^{p}\oplus \overline {F}^{k-p+1}$;
$V_\mathbb {C}=F^{p}\oplus \overline {F}^{k-p+1}$;(ii)
 $B(u, v) = 0$ for all
$B(u, v) = 0$ for all  $(u,v)\in F^p \times F^{k-p+1}$;
$(u,v)\in F^p \times F^{k-p+1}$;(iii)
 $i^{p-q}B(v, \bar v)>0$ for all
$i^{p-q}B(v, \bar v)>0$ for all  $v\in (F^p \cap \overline {F}^{q})\backslash \{0\}$ with
$v\in (F^p \cap \overline {F}^{q})\backslash \{0\}$ with  $p+q=k$.
$p+q=k$.
Remark 5.1 The existence of a Hodge structure of weight ![]() $k$ implies that
$k$ implies that ![]() $B$ is non-degenerate and antisymmetric for odd
$B$ is non-degenerate and antisymmetric for odd ![]() $k$ or symmetric for even
$k$ or symmetric for even ![]() $k$.
$k$.
For ![]() $p+q = k$, define
$p+q = k$, define ![]() $V^{p,q} = F^p \cap \overline F^{q}$. Then
$V^{p,q} = F^p \cap \overline F^{q}$. Then ![]() $V^{p,q}$ is a complement of
$V^{p,q}$ is a complement of ![]() $F^{p+1}$ in
$F^{p+1}$ in ![]() $F^p$. In particular, we have a decomposition
$F^p$. In particular, we have a decomposition
The Hodge numbers of the Hodge structure are the numbers ![]() $h^{p,q} \overset {\text {def}}= \dim _\mathbb {C}(V^{p,q})$.
$h^{p,q} \overset {\text {def}}= \dim _\mathbb {C}(V^{p,q})$.
Let ![]() $\mathbb {S}=\mathrm {Res}_{\mathbb {C}/\mathbb {R}}\mathbb {G}_m$ denote the Deligne torus, i.e. the restriction of scalars of the multiplicative group
$\mathbb {S}=\mathrm {Res}_{\mathbb {C}/\mathbb {R}}\mathbb {G}_m$ denote the Deligne torus, i.e. the restriction of scalars of the multiplicative group ![]() $\mathbb {G}_m$ from
$\mathbb {G}_m$ from ![]() $\mathbb {C}$ to
$\mathbb {C}$ to ![]() $\mathbb {R}$. Then
$\mathbb {R}$. Then ![]() $\mathbb {S}(\mathbb {R})=\mathbb {C}^\times$ seen as an algebraic group over
$\mathbb {S}(\mathbb {R})=\mathbb {C}^\times$ seen as an algebraic group over ![]() $\mathbb {R}$. Every Hodge structure on
$\mathbb {R}$. Every Hodge structure on ![]() $(V_\mathbb {Z}, B)$ induces a representation
$(V_\mathbb {Z}, B)$ induces a representation ![]() $\varphi : \mathbb {S}(\mathbb {R}) \to \operatorname {GL}(V_\mathbb {R})$ given by
$\varphi : \mathbb {S}(\mathbb {R}) \to \operatorname {GL}(V_\mathbb {R})$ given by
on ![]() $u\in V^{p,q}$.
$u\in V^{p,q}$.
Let ![]() $k\in \mathbb {Z}$ and
$k\in \mathbb {Z}$ and ![]() $\underline {h} = (h_{p,q})_{p+q = k} \in \mathbb {N}^{k+1}$ be such that
$\underline {h} = (h_{p,q})_{p+q = k} \in \mathbb {N}^{k+1}$ be such that ![]() $h_{p,q} = h_{q,p}$ and
$h_{p,q} = h_{q,p}$ and ![]() $\sum _{p=0}^k h^{p,q} = d$. The period domain of Hodge structure of weight
$\sum _{p=0}^k h^{p,q} = d$. The period domain of Hodge structure of weight ![]() $k$ and Hodge numbers
$k$ and Hodge numbers ![]() $(h_{p,q})_{p+q = k}$ is the set
$(h_{p,q})_{p+q = k}$ is the set ![]() $\mathcal {D}$ of all filtrations
$\mathcal {D}$ of all filtrations ![]() $(F^{p})_{0\leq p\leq k}$ which define a Hodge structure of weight
$(F^{p})_{0\leq p\leq k}$ which define a Hodge structure of weight ![]() $k$ and Hodge numbers
$k$ and Hodge numbers ![]() $h^{p,q}$ on
$h^{p,q}$ on ![]() $(V_\mathbb {Z},B)$. It is a complex manifold homogeneous under the action of the group
$(V_\mathbb {Z},B)$. It is a complex manifold homogeneous under the action of the group ![]() $\operatorname {Aut}_\mathbb {R}(B)$, and the stabilizer of a point is a compact subgroup of
$\operatorname {Aut}_\mathbb {R}(B)$, and the stabilizer of a point is a compact subgroup of ![]() $\operatorname {Aut}_\mathbb {R}(B)$.
$\operatorname {Aut}_\mathbb {R}(B)$.
The period domain ![]() $\mathcal {D}$ is an open subset of the compactified period domain
$\mathcal {D}$ is an open subset of the compactified period domain ![]() $\widehat {\mathcal {D}}$ of complex flags
$\widehat {\mathcal {D}}$ of complex flags ![]() $0\subseteq F^{k}\subseteq \cdots \subseteq F^0 = V_\mathbb {C}$ such that
$0\subseteq F^{k}\subseteq \cdots \subseteq F^0 = V_\mathbb {C}$ such that ![]() $F^{k-p} = {F^p}^\bot$ and
$F^{k-p} = {F^p}^\bot$ and ![]() $\dim _\mathbb {C}(F^p/F^{p+1}) = h^{p,k-p}$ for all
$\dim _\mathbb {C}(F^p/F^{p+1}) = h^{p,k-p}$ for all ![]() $p$. The compactified period domain is a flag variety of the group
$p$. The compactified period domain is a flag variety of the group ![]() $\operatorname {Aut}_\mathbb {C}(B)$ (i.e. a quotient of
$\operatorname {Aut}_\mathbb {C}(B)$ (i.e. a quotient of ![]() $\operatorname {Aut}_\mathbb {C}(B)$ by a parabolic subgroup).
$\operatorname {Aut}_\mathbb {C}(B)$ by a parabolic subgroup).
Let ![]() $\mathcal {U}$ denote the trivial complex vector bundle
$\mathcal {U}$ denote the trivial complex vector bundle ![]() $\mathcal {D} \times V_\mathbb {C}$ equipped with the action of
$\mathcal {D} \times V_\mathbb {C}$ equipped with the action of ![]() $\operatorname {Aut}_\mathbb {R}(B)$ given by the tautological linear action in the fibers. By construction, this bundle admits a
$\operatorname {Aut}_\mathbb {R}(B)$ given by the tautological linear action in the fibers. By construction, this bundle admits a ![]() $\operatorname {Aut}_\mathbb {R}(B)$-invariant real structure and a complex bilinear pairing
$\operatorname {Aut}_\mathbb {R}(B)$-invariant real structure and a complex bilinear pairing ![]() $B$ as well as a universal Hodge decomposition, i.e. a smooth decomposition as a direct sum of
$B$ as well as a universal Hodge decomposition, i.e. a smooth decomposition as a direct sum of ![]() $G_\mathbb {R}$-equivariant complex vector bundles
$G_\mathbb {R}$-equivariant complex vector bundles ![]() $\mathcal {U}^{p,q}$ such that, at a point
$\mathcal {U}^{p,q}$ such that, at a point ![]() $x$, the induced decomposition of
$x$, the induced decomposition of ![]() $\mathcal {U}_x = V\otimes _\mathbb {Z} \mathbb {C}$ is the Hodge decomposition associated with
$\mathcal {U}_x = V\otimes _\mathbb {Z} \mathbb {C}$ is the Hodge decomposition associated with ![]() $x$.
$x$.
Now let ![]() $X$ be a complex analytic variety. A (polarized) variation of Hodge structure of weight
$X$ be a complex analytic variety. A (polarized) variation of Hodge structure of weight ![]() $k$ over
$k$ over ![]() $X$ is the data of:
$X$ is the data of:
(i) a local system
 $\mathbb {V}_\mathbb {Z}$ of free
$\mathbb {V}_\mathbb {Z}$ of free  $\mathbb {Z}$-modules of finite rank
$\mathbb {Z}$-modules of finite rank  $d$ with a flat bilinear pairing
$d$ with a flat bilinear pairing  $B:\mathbb {V}_\mathbb {Z}\otimes \mathbb {V}_\mathbb {Z}\rightarrow \underline {\mathbb {Z}}_X$;
$B:\mathbb {V}_\mathbb {Z}\otimes \mathbb {V}_\mathbb {Z}\rightarrow \underline {\mathbb {Z}}_X$;(ii) a decreasing filtration
 $\mathcal {F}^{\bullet }\mathcal {V}$ on
$\mathcal {F}^{\bullet }\mathcal {V}$ on  $\mathcal {V}=\mathbb {V}_\mathbb {Z}\otimes _{\underline {\mathbb {Z}}_X} \mathcal {O}_X$ by holomorphic sub-vector bundles
$\mathcal {V}=\mathbb {V}_\mathbb {Z}\otimes _{\underline {\mathbb {Z}}_X} \mathcal {O}_X$ by holomorphic sub-vector bundles  $0\subseteq \mathcal {F}^{k}\mathcal {V}\subseteq \cdots \subseteq \mathcal {F}^0\mathcal {V}=\mathcal {V}$;
$0\subseteq \mathcal {F}^{k}\mathcal {V}\subseteq \cdots \subseteq \mathcal {F}^0\mathcal {V}=\mathcal {V}$;
which satisfy the following conditions.
(a) Hodge property: for every
 $x\in X$, the flag
$x\in X$, the flag  $0\subseteq \mathcal {F}^{k}\mathcal {V}_x\subseteq \cdots \subseteq \mathcal {F}^0\mathcal {V}_x\overset {\text {def}}= \mathcal {V}_x$ is a Hodge structure on
$0\subseteq \mathcal {F}^{k}\mathcal {V}_x\subseteq \cdots \subseteq \mathcal {F}^0\mathcal {V}_x\overset {\text {def}}= \mathcal {V}_x$ is a Hodge structure on  ${\mathbb {V}_{\mathbb {Z},x}}$.
${\mathbb {V}_{\mathbb {Z},x}}$.(b) Griffiths’ transversality: the flat connection
 $\nabla$ associated on
$\nabla$ associated on  $\mathbb {V}_\mathbb {Z}\otimes \mathcal {O}_X$ satisfies
$\mathbb {V}_\mathbb {Z}\otimes \mathcal {O}_X$ satisfies
 \[ \nabla(\mathcal{F}^{p}\mathcal{V})\subseteq \mathcal{F}^{p-1} \mathcal{V}\otimes \Omega^{1}_X \text{ for } 0\leq p\leq k. \]
\[ \nabla(\mathcal{F}^{p}\mathcal{V})\subseteq \mathcal{F}^{p-1} \mathcal{V}\otimes \Omega^{1}_X \text{ for } 0\leq p\leq k. \]
Let ![]() $\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a variation of Hodge structure of weight
$\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a variation of Hodge structure of weight ![]() $k$ over
$k$ over ![]() $X$. Its Hodge decomposition is the (
$X$. Its Hodge decomposition is the (![]() $C^{\infty }$) decomposition
$C^{\infty }$) decomposition
where ![]() $\mathcal {V}^{p,q} = \mathcal {F}^p\mathcal {V} \cap \overline {\mathcal {F}}^{k-p} \mathcal {V}$, and its Hodge numbers are
$\mathcal {V}^{p,q} = \mathcal {F}^p\mathcal {V} \cap \overline {\mathcal {F}}^{k-p} \mathcal {V}$, and its Hodge numbers are
Now let ![]() $\pi :\widetilde {X}\to X$ be the universal cover of
$\pi :\widetilde {X}\to X$ be the universal cover of ![]() $X$ and
$X$ and ![]() $x$ and arbitrary point in
$x$ and arbitrary point in ![]() $\widetilde {X}$. The local system
$\widetilde {X}$. The local system ![]() $\pi ^*\mathbb {V}_\mathbb {Z}$ is trivial, and one obtains a map
$\pi ^*\mathbb {V}_\mathbb {Z}$ is trivial, and one obtains a map
such that ![]() $\widetilde {f}(y)$ is the Hodge structure
$\widetilde {f}(y)$ is the Hodge structure ![]() $\mathcal {F}^\bullet \mathcal {V}_y$ on
$\mathcal {F}^\bullet \mathcal {V}_y$ on ![]() $(\pi ^*{\mathbb {V}_{\mathbb {Z}}})_y = {\mathbb {V}_{\mathbb {Z},x}}$. This map is equivariant with respect to the monodromy
$(\pi ^*{\mathbb {V}_{\mathbb {Z}}})_y = {\mathbb {V}_{\mathbb {Z},x}}$. This map is equivariant with respect to the monodromy ![]() $\rho :\pi _1(X) \to G_\mathbb {Z} = \operatorname {Aut}({\mathbb {V}_{\mathbb {Z},x}})$ of the local system and thus factors to a map
$\rho :\pi _1(X) \to G_\mathbb {Z} = \operatorname {Aut}({\mathbb {V}_{\mathbb {Z},x}})$ of the local system and thus factors to a map
called the period map of the variation of Hodge structure. There are canonical isomorphisms
In terms of the period map, Griffiths’ transversality condition admits the following interpretation. Let ![]() $x$ be a point in
$x$ be a point in ![]() $\mathcal {D}$ and let
$\mathcal {D}$ and let ![]() $\varphi : \mathbb {S} \to G_\mathbb {R}$ be the associated representation of the Deligne torus. Then the Lie algebra
$\varphi : \mathbb {S} \to G_\mathbb {R}$ be the associated representation of the Deligne torus. Then the Lie algebra ![]() $\mathfrak {g}_\mathbb {C}$ decomposes under the adjoint action as
$\mathfrak {g}_\mathbb {C}$ decomposes under the adjoint action as
where
The subalgebra ![]() $\mathfrak {g}^{0,0}$ is the Lie algebra of the stabilizer of
$\mathfrak {g}^{0,0}$ is the Lie algebra of the stabilizer of ![]() $x$, and its complement identifies with the complexified tangent space to
$x$, and its complement identifies with the complexified tangent space to ![]() $\mathcal {D}$ at
$\mathcal {D}$ at ![]() $x$. The eigenspace of the complex structure on
$x$. The eigenspace of the complex structure on ![]() $T_x \mathcal {D}$ for
$T_x \mathcal {D}$ for ![]() $i$ is the subspace
$i$ is the subspace ![]() $\bigoplus _{p<0} \mathfrak {g}^{p,-p}$.
$\bigoplus _{p<0} \mathfrak {g}^{p,-p}$.
The subspace ![]() $\mathfrak {g}^{1,-1}\oplus \mathfrak {g}^{-1,1}$ is the complexification of a well-defined subspace
$\mathfrak {g}^{1,-1}\oplus \mathfrak {g}^{-1,1}$ is the complexification of a well-defined subspace ![]() $W_x \subset T_x \mathcal {D}$. This defines a holomorphic
$W_x \subset T_x \mathcal {D}$. This defines a holomorphic ![]() $G_\mathbb {R}$-invariant distribution of
$G_\mathbb {R}$-invariant distribution of ![]() $T_x \mathcal {D}$ called the Griffiths’ distribution. Now, Griffiths’ transversality condition states precisely that the period map is tangent to the Griffiths’ distribution.
$T_x \mathcal {D}$ called the Griffiths’ distribution. Now, Griffiths’ transversality condition states precisely that the period map is tangent to the Griffiths’ distribution.
5.2 Hodge loci and transversality
Let ![]() $(V, B)$ be a lattice with an integral bilinear pairing. A Hodge structure on
$(V, B)$ be a lattice with an integral bilinear pairing. A Hodge structure on ![]() $V$ induces a Hodge structure on
$V$ induces a Hodge structure on ![]() $T^{k,l}V \overset {\text {def}}= V^{\otimes k} \otimes {V^\vee }^{\otimes l}$ for all
$T^{k,l}V \overset {\text {def}}= V^{\otimes k} \otimes {V^\vee }^{\otimes l}$ for all ![]() $k,l$, whose Hodge decomposition is given by the diagonalization of the induced representation
$k,l$, whose Hodge decomposition is given by the diagonalization of the induced representation ![]() $\varphi : \mathbb {S}(\mathbb {R}) \to \operatorname {End}(T^{k,l}V\otimes _\mathbb {Z} \mathbb {C})$ of the Deligne torus. Let
$\varphi : \mathbb {S}(\mathbb {R}) \to \operatorname {End}(T^{k,l}V\otimes _\mathbb {Z} \mathbb {C})$ of the Deligne torus. Let ![]() $\mathbb {U}^1\subset \mathbb {S}(\mathbb {R})$ denote the unit circle.
$\mathbb {U}^1\subset \mathbb {S}(\mathbb {R})$ denote the unit circle.
Definition 5.2 The Mumford–Tate group ![]() $MT_{\varphi }$ of
$MT_{\varphi }$ of ![]() $(V,B)$ is the smallest
$(V,B)$ is the smallest ![]() $\mathbb {Q}$-algebraic subgroup of
$\mathbb {Q}$-algebraic subgroup of ![]() $\mathrm {GL}(V_\mathbb {R})$ which contains
$\mathrm {GL}(V_\mathbb {R})$ which contains ![]() $\varphi (\mathbb {C}^\times )$. The special Mumford–Tate group is the smallest
$\varphi (\mathbb {C}^\times )$. The special Mumford–Tate group is the smallest ![]() $\mathbb {Q}$-algebraic subgroup
$\mathbb {Q}$-algebraic subgroup ![]() $sMT_{\varphi }$ which contains
$sMT_{\varphi }$ which contains ![]() $\varphi (\mathbb {U}^1)$.
$\varphi (\mathbb {U}^1)$.
The algebra of Hodge classes is the bigraded ![]() $\mathbb {Z}$-subalgebra
$\mathbb {Z}$-subalgebra ![]() $\operatorname {Hdg}^{\bullet, \bullet }(\varphi ) \subset T^{\bullet,\bullet }V$ fixed by
$\operatorname {Hdg}^{\bullet, \bullet }(\varphi ) \subset T^{\bullet,\bullet }V$ fixed by ![]() $\varphi (\mathbb {U}^1)$.
$\varphi (\mathbb {U}^1)$.
Now let ![]() $v$ be a vector in
$v$ be a vector in ![]() $T^{\bullet, \bullet }V$. The Hodge domain of
$T^{\bullet, \bullet }V$. The Hodge domain of ![]() $v$ is the set of variations of Hodge structure
$v$ is the set of variations of Hodge structure ![]() $\varphi$ on
$\varphi$ on ![]() $V$ such that
$V$ such that ![]() $\operatorname {Hdg}^{\bullet, \bullet }(\varphi )$ contains
$\operatorname {Hdg}^{\bullet, \bullet }(\varphi )$ contains ![]() $v$. The connected components of the Hodge domain of
$v$. The connected components of the Hodge domain of ![]() $v$ are homogeneous under the stabilizer of
$v$ are homogeneous under the stabilizer of ![]() $v$ in
$v$ in ![]() $G_\mathbb {R}$. They are called Mumford–Tate domains, and the stabilizer of such components are Mumford–Tate groups.
$G_\mathbb {R}$. They are called Mumford–Tate domains, and the stabilizer of such components are Mumford–Tate groups.
Remark 5.3 If ![]() $\operatorname {Hdg}^{\bullet, \bullet }(\varphi )$ contains a set
$\operatorname {Hdg}^{\bullet, \bullet }(\varphi )$ contains a set ![]() $A$, then it contains the subalgebra spanned by
$A$, then it contains the subalgebra spanned by ![]() $A$. Conversely, for every bigraded subalgebra
$A$. Conversely, for every bigraded subalgebra ![]() $H^{\bullet,\bullet }$ of
$H^{\bullet,\bullet }$ of ![]() $T^{\bullet,\bullet }V$, there exists
$T^{\bullet,\bullet }V$, there exists ![]() $v\in H^{\bullet,\bullet }$ such that
$v\in H^{\bullet,\bullet }$ such that
In particular, intersections of Hodge or Mumford–Tate domains are again Hodge and Mumford–Tate domains.
As Mumford–Tate groups are defined over ![]() $\mathbb {Q}$, the projection of a Mumford–Tate domain
$\mathbb {Q}$, the projection of a Mumford–Tate domain ![]() $H_\mathbb {R}/L_\mathbb {R}$ to
$H_\mathbb {R}/L_\mathbb {R}$ to ![]() $G_\mathbb {Z} \backslash G_\mathbb {R}/K_\mathbb {R}$ factors to a proper immersion of
$G_\mathbb {Z} \backslash G_\mathbb {R}/K_\mathbb {R}$ factors to a proper immersion of ![]() $H_\mathbb {Z} \backslash H_\mathbb {R}/L_\mathbb {R}$.
$H_\mathbb {Z} \backslash H_\mathbb {R}/L_\mathbb {R}$.
Now let ![]() $X$ be a connected analytic variety equipped with a variation of Hodge structure
$X$ be a connected analytic variety equipped with a variation of Hodge structure ![]() $(\mathbb {V}_\mathbb {Z},B,\mathcal {F}^\bullet \mathcal {V})$ of weight
$(\mathbb {V}_\mathbb {Z},B,\mathcal {F}^\bullet \mathcal {V})$ of weight ![]() $k$ and Hodge numbers
$k$ and Hodge numbers ![]() $(h^{p,q})_{p+q=k}$. We assume that the period map of
$(h^{p,q})_{p+q=k}$. We assume that the period map of ![]() $X$ is generically immersive.
$X$ is generically immersive.
Let ![]() $G_\mathbb {R}/K_\mathbb {R}$ be a Mumford–Tate domain containing
$G_\mathbb {R}/K_\mathbb {R}$ be a Mumford–Tate domain containing ![]() $\widetilde {X}$. Then the monodromy representation takes values in
$\widetilde {X}$. Then the monodromy representation takes values in ![]() $G_\mathbb {Z}$ and at every point
$G_\mathbb {Z}$ and at every point ![]() $y\in \widetilde {X}$ the algebra
$y\in \widetilde {X}$ the algebra ![]() $\operatorname {Hdg}^{\bullet, \bullet }(\varphi )$ of Hodge classes at
$\operatorname {Hdg}^{\bullet, \bullet }(\varphi )$ of Hodge classes at ![]() $y$ contains the subalgebra
$y$ contains the subalgebra ![]() $H^{\bullet, \bullet }$ fixed by
$H^{\bullet, \bullet }$ fixed by ![]() $G_\mathbb {R}$.
$G_\mathbb {R}$.
The variation of Hodge structure ![]() $X$ is called Hodge generic in
$X$ is called Hodge generic in ![]() $G_\mathbb {R}/K_\mathbb {R}$ if there is no proper Hodge subdomain of
$G_\mathbb {R}/K_\mathbb {R}$ if there is no proper Hodge subdomain of ![]() $G_\mathbb {R}/K_\mathbb {R}$ containing
$G_\mathbb {R}/K_\mathbb {R}$ containing ![]() $\widetilde {X}$. In that case, at a generic point of
$\widetilde {X}$. In that case, at a generic point of ![]() $X$, the algebra of Hodge classes is exactly
$X$, the algebra of Hodge classes is exactly ![]() $(T^{\bullet,\bullet } \mathbb {V})^{G_\mathbb {R}}$ and the Mumford–Tate group is a rational form of
$(T^{\bullet,\bullet } \mathbb {V})^{G_\mathbb {R}}$ and the Mumford–Tate group is a rational form of ![]() $G$. We state the following definition.
$G$. We state the following definition.
Definition 5.4 Let ![]() $G_\mathbb {R}/K_\mathbb {R}$ be the smallest Mumford–Tate domain containing
$G_\mathbb {R}/K_\mathbb {R}$ be the smallest Mumford–Tate domain containing ![]() $X$. The Hodge locus of
$X$. The Hodge locus of ![]() $\widetilde {X}$ is the set of points at which the algebra of Hodge classes contains strictly
$\widetilde {X}$ is the set of points at which the algebra of Hodge classes contains strictly ![]() $(T^{\bullet,\bullet } \mathbb {V})^{G_\mathbb {R}}$. The Hodge locus of
$(T^{\bullet,\bullet } \mathbb {V})^{G_\mathbb {R}}$. The Hodge locus of ![]() $X$ is its projection under the covering map.
$X$ is its projection under the covering map.
The Hodge locus of ![]() $X$ is the intersection of
$X$ is the intersection of ![]() $X$ with the countable union of all the projections modulo
$X$ with the countable union of all the projections modulo ![]() $G_\mathbb {Z}$ of the Mumford–Tate subdomains of
$G_\mathbb {Z}$ of the Mumford–Tate subdomains of ![]() $G_\mathbb {R}/K_\mathbb {R}$. To be more precise, let
$G_\mathbb {R}/K_\mathbb {R}$. To be more precise, let ![]() $G_\mathbb {R}/K_\mathbb {R}$ be any Mumford–Tate domain containing
$G_\mathbb {R}/K_\mathbb {R}$ be any Mumford–Tate domain containing ![]() $\widetilde {X}$ and let
$\widetilde {X}$ and let ![]() $H$ be an algebraic subgroup of
$H$ be an algebraic subgroup of ![]() $G$ defined over
$G$ defined over ![]() $\mathbb {Q}$. We state the following definition.
$\mathbb {Q}$. We state the following definition.
Definition 5.5 The Hodge locus of type ![]() $H$ is the set of points in
$H$ is the set of points in ![]() $\widetilde {X}$ whose Mumford–Tate group is conjugated over
$\widetilde {X}$ whose Mumford–Tate group is conjugated over ![]() $\mathbb {R}$ to a subgroup of
$\mathbb {R}$ to a subgroup of ![]() $H$. The Hodge locus of type
$H$. The Hodge locus of type ![]() $H$ in
$H$ in ![]() $X$ is its projection by the covering map.
$X$ is its projection by the covering map.
The Hodge locus of type ![]() $H$ is the intersection of
$H$ is the intersection of ![]() $\widetilde {X}$ with the union of Mumford–Tate domains
$\widetilde {X}$ with the union of Mumford–Tate domains ![]() $\bigcup _{g\in G_\mathbb {R}} g H_\mathbb {R}/L_\mathbb {R}$, for all
$\bigcup _{g\in G_\mathbb {R}} g H_\mathbb {R}/L_\mathbb {R}$, for all ![]() $g\in G_\mathbb {R}$ such that
$g\in G_\mathbb {R}$ such that ![]() $g H_\mathbb {R} g^{-1}$ is
$g H_\mathbb {R} g^{-1}$ is ![]() $\mathbb {Q}$-subgroup. This leads to the following definition.
$\mathbb {Q}$-subgroup. This leads to the following definition.
Definition 5.6 The transverse Hodge locus of type ![]() $H$ is the set of smooth points of
$H$ is the set of smooth points of ![]() $X$ for which there exists
$X$ for which there exists ![]() $g\in G_\mathbb {R}$ such that
$g\in G_\mathbb {R}$ such that ![]() $gHg^{-1}$ is a
$gHg^{-1}$ is a ![]() $\mathbb {Q}$-group and
$\mathbb {Q}$-group and ![]() $\widetilde {X}$ and
$\widetilde {X}$ and ![]() $g H_\mathbb {R}/L_\mathbb {R}$ intersect transversally at
$g H_\mathbb {R}/L_\mathbb {R}$ intersect transversally at ![]() $x$.
$x$.
If ![]() $X$ is Hodge generic in
$X$ is Hodge generic in ![]() $\mathcal {D}$, the transverse Hodge locus (of type
$\mathcal {D}$, the transverse Hodge locus (of type ![]() $H$) is called the typical Hodge locus (of type
$H$) is called the typical Hodge locus (of type ![]() $H$).
$H$).
As Hodge loci are intersections of ![]() $X$ with locally homogeneous sub-spaces of
$X$ with locally homogeneous sub-spaces of ![]() $G_\mathbb {Z} \backslash \mathcal {D}$, we can hope to apply our equidistribution result in this setting. However, in order for it to be effective, one needs a generic transversality property between
$G_\mathbb {Z} \backslash \mathcal {D}$, we can hope to apply our equidistribution result in this setting. However, in order for it to be effective, one needs a generic transversality property between ![]() $X$ and
$X$ and ![]() $H/L$.
$H/L$.
Definition 5.7 We say that ![]() $X$ is generically transverse to
$X$ is generically transverse to ![]() $H$-orbits at a smooth point
$H$-orbits at a smooth point ![]() $x$ if there exists
$x$ if there exists ![]() $g\in G_\mathbb {R}$ such that
$g\in G_\mathbb {R}$ such that ![]() $gH_\mathbb {R}/L_\mathbb {R}$ and
$gH_\mathbb {R}/L_\mathbb {R}$ and ![]() $\widetilde {X}$ intersect transversally at (some lift of)
$\widetilde {X}$ intersect transversally at (some lift of) ![]() $x$.
$x$.
We say that ![]() $X$ is generically transverse to
$X$ is generically transverse to ![]() $H$-orbits if there exists a smooth point at which it is generically transverse.
$H$-orbits if there exists a smooth point at which it is generically transverse.
Remark 5.8 If ![]() $X$ is generically transverse to
$X$ is generically transverse to ![]() $H$-orbits, then the set of points
$H$-orbits, then the set of points ![]() $x$ at which it is generically transverse is an open and dense analytic subset of
$x$ at which it is generically transverse is an open and dense analytic subset of ![]() $X$.
$X$.
Proposition 5.9 Let ![]() $x$ be a point in
$x$ be a point in ![]() $X$. Then
$X$. Then ![]() $X$ is generically transverse to
$X$ is generically transverse to ![]() $H$-orbits at
$H$-orbits at ![]() $x$ if and only if the pull–push form
$x$ if and only if the pull–push form ![]() $\pi _*p^*\omega _{G/H}$ is non-zero at
$\pi _*p^*\omega _{G/H}$ is non-zero at ![]() $x$.
$x$.
As the consequence, we get the following density criterion for the transverse Hodge locus of type ![]() $H$.
$H$.
Theorem 5.10 The following propositions are equivalent:
(i) the transverse Hodge locus of type
 $H$ is non-empty;
$H$ is non-empty;(ii) the transverse Hodge locus of type
 $H$ is analytically dense in
$H$ is analytically dense in  $X$;
$X$;(iii)
 $X$ is generically transverse to
$X$ is generically transverse to  $H$-orbits;
$H$-orbits;(iv) the pull–push form
 $\pi _*p^*\omega _{G/H}$ is not identically zero on
$\pi _*p^*\omega _{G/H}$ is not identically zero on  $X$.
$X$.
Proof of Proposition 5.9 Let ![]() $d$ be half of the degree of the form
$d$ be half of the degree of the form ![]() $\pi _*p^*\omega _{G/H}$.
$\pi _*p^*\omega _{G/H}$.
Assume that ![]() $X$ is generically transverse to
$X$ is generically transverse to ![]() $H$-orbits at
$H$-orbits at ![]() $x$, and let
$x$, and let ![]() $g\in G$ be such that
$g\in G$ be such that ![]() $x\in gH/L$ and
$x\in gH/L$ and
Let ![]() $u$ be a multivector as in Proposition 4.3. As
$u$ be a multivector as in Proposition 4.3. As ![]() $T_x(gH/L)_\mathbb {C}$ is in the kernel of
$T_x(gH/L)_\mathbb {C}$ is in the kernel of ![]() $\iota _u p^*\omega _{G/H}$, there exists holomorphic vector fields
$\iota _u p^*\omega _{G/H}$, there exists holomorphic vector fields ![]() $X_1,\ldots,X_d$ on
$X_1,\ldots,X_d$ on ![]() $X$ defined on a neighborhood of
$X$ defined on a neighborhood of ![]() $x$ such that
$x$ such that
For every ![]() $k\in K$, we have by Corollary 4.6,
$k\in K$, we have by Corollary 4.6,
and this inequality is strict in an open neighborhood of the basepoint of ![]() $K/L$. Hence, by integrating over
$K/L$. Hence, by integrating over ![]() $k$ and using Definition 4.1, we get
$k$ and using Definition 4.1, we get ![]() $\pi _*p^*\omega _{G/H}\neq 0$ at
$\pi _*p^*\omega _{G/H}\neq 0$ at ![]() $x$.
$x$.
Conversely, assume that ![]() $X$ is not generically transverse at
$X$ is not generically transverse at ![]() $x$. Then for every
$x$. Then for every ![]() $g\in G$, we have
$g\in G$, we have ![]() $T_xX+T_x(gH/L)\subsetneq T_xG/K$. Hence, for every
$T_xX+T_x(gH/L)\subsetneq T_xG/K$. Hence, for every ![]() $d$-uple of
$d$-uple of ![]() $\mathbb {C}$-linearly independent vectors
$\mathbb {C}$-linearly independent vectors ![]() $X_1,\ldots,X_{d}$ in
$X_1,\ldots,X_{d}$ in ![]() $T_xX$, the intersection of the subspaces
$T_xX$, the intersection of the subspaces ![]() $\mathrm {span}_\mathbb {R}(X_1,\overline {X}_1,\ldots,X_{d},\overline {X}_{d})$ and
$\mathrm {span}_\mathbb {R}(X_1,\overline {X}_1,\ldots,X_{d},\overline {X}_{d})$ and ![]() $T_x(gH/L)_\mathbb {C}$ is non-empty. Hence, the form
$T_x(gH/L)_\mathbb {C}$ is non-empty. Hence, the form ![]() $\iota _{u}\omega _{G/H}$ vanishes on the multi-vector
$\iota _{u}\omega _{G/H}$ vanishes on the multi-vector ![]() $X_1\wedge \overline {X}_1\ldots X_{d}\wedge \overline {X}_d$. The same is true for
$X_1\wedge \overline {X}_1\ldots X_{d}\wedge \overline {X}_d$. The same is true for ![]() $Ad(k)^*(\iota _u\overline {p}^*\omega _{G/H})$ for all
$Ad(k)^*(\iota _u\overline {p}^*\omega _{G/H})$ for all ![]() $k\in K$. By integrating, we get that
$k\in K$. By integrating, we get that ![]() $\pi _*p^*\omega _{G/H}$ vanishes at
$\pi _*p^*\omega _{G/H}$ vanishes at ![]() $x$. Hence, the result.
$x$. Hence, the result.
Proof of Theorem 5.10 The implication ![]() $({\rm ii})\Rightarrow ({\rm i})$ and
$({\rm ii})\Rightarrow ({\rm i})$ and ![]() $({\rm i})\Rightarrow ({\rm iii})$ are obvious, and the equivalence
$({\rm i})\Rightarrow ({\rm iii})$ are obvious, and the equivalence ![]() $({\rm iii})\Rightarrow ({\rm iv})$ readily follows from Proposition 5.9. We only have to prove
$({\rm iii})\Rightarrow ({\rm iv})$ readily follows from Proposition 5.9. We only have to prove ![]() $({\rm iii})\Rightarrow ({\rm i})$.
$({\rm iii})\Rightarrow ({\rm i})$.
By Remark 5.8, the set of points where ![]() $X$ is transverse to
$X$ is transverse to ![]() $H$-orbits is open and dense. Let
$H$-orbits is open and dense. Let ![]() $x$ be such a point and
$x$ be such a point and ![]() $g\in G_\mathbb {R}$ such that
$g\in G_\mathbb {R}$ such that ![]() $\widetilde {X}$ and
$\widetilde {X}$ and ![]() $gH_\mathbb {R}/L_\mathbb {R}$ intersect transversally at
$gH_\mathbb {R}/L_\mathbb {R}$ intersect transversally at ![]() $x$. By weak approximation,
$x$. By weak approximation, ![]() $G(\mathbb {Q})$ is analytically dense in
$G(\mathbb {Q})$ is analytically dense in ![]() $G(\mathbb {R})$. Thus, there exists a sequence
$G(\mathbb {R})$. Thus, there exists a sequence ![]() $g_n \in G_\mathbb {Q}$ converging to
$g_n \in G_\mathbb {Q}$ converging to ![]() $g$. For
$g$. For ![]() $n$ large enough, by stability of transversality,
$n$ large enough, by stability of transversality, ![]() $g_n H_\mathbb {R}/L_\mathrm H$ intersects
$g_n H_\mathbb {R}/L_\mathrm H$ intersects ![]() $\widetilde {X}$ transversally at a point
$\widetilde {X}$ transversally at a point ![]() $x_n$ such that
$x_n$ such that ![]() $x_n \underset {n\to +\infty }{\longrightarrow } x$. As
$x_n \underset {n\to +\infty }{\longrightarrow } x$. As ![]() $g_n \in G_\mathbb {Q}$,
$g_n \in G_\mathbb {Q}$, ![]() $g_n Hg_n^{-1}$ is a
$g_n Hg_n^{-1}$ is a ![]() $\mathbb {Q}$-subgroup of
$\mathbb {Q}$-subgroup of ![]() $G$, hence
$G$, hence ![]() $x_n$ belongs to the transverse Hodge locus of type
$x_n$ belongs to the transverse Hodge locus of type ![]() $H$.
$H$.
Unfortunately, in many situations, variations of Hodge structure are never generically transverse to ![]() $H/L$. Indeed, Griffiths’ transversality constrains their tangent space to be contained in the Griffith distribution, so that it cannot supplement
$H/L$. Indeed, Griffiths’ transversality constrains their tangent space to be contained in the Griffith distribution, so that it cannot supplement ![]() $T_x(H/L)$ in other directions.
$T_x(H/L)$ in other directions.
To be more precise, let ![]() $H/L \subset G/K \subset \mathcal {D}$ be Mumford–Tate domains. Let
$H/L \subset G/K \subset \mathcal {D}$ be Mumford–Tate domains. Let ![]() $\varphi :\mathbb {U}^1 \to H$ be the restriction of the representation at a point
$\varphi :\mathbb {U}^1 \to H$ be the restriction of the representation at a point ![]() $x\in H/L$ of the Deligne torus to the unit circle. Then both
$x\in H/L$ of the Deligne torus to the unit circle. Then both ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\mathfrak {h}$ are invariant under the adjoint action of
$\mathfrak {h}$ are invariant under the adjoint action of ![]() $\varphi$. We thus have decompositions
$\varphi$. We thus have decompositions
 \[ \mathfrak{g}_\mathbb{C} = \bigoplus_{p=-k}^k \mathfrak{g}^{p,-p}~,\quad \mathfrak{h}_\mathbb{C} = \bigoplus_{p=-k}^k \mathfrak{h}^{p,-p} \]
\[ \mathfrak{g}_\mathbb{C} = \bigoplus_{p=-k}^k \mathfrak{g}^{p,-p}~,\quad \mathfrak{h}_\mathbb{C} = \bigoplus_{p=-k}^k \mathfrak{h}^{p,-p} \]
with ![]() $\mathfrak {h}^{p,-p}\subseteq \mathfrak {g}^{p,-p}$. Note that
$\mathfrak {h}^{p,-p}\subseteq \mathfrak {g}^{p,-p}$. Note that ![]() $\mathfrak {g}^{0,0} = \mathfrak {k}$ and
$\mathfrak {g}^{0,0} = \mathfrak {k}$ and ![]() $\mathfrak {h}^{0,0} = \mathfrak {l}$.
$\mathfrak {h}^{0,0} = \mathfrak {l}$.
Proposition 5.11 The following are equivalent.
(i) There exists a smooth variation of Hodge structure in
 $G/K$ which is generically transverse to
$G/K$ which is generically transverse to  $H/L$.
$H/L$.(ii) For all
 $|p|\geq 2$,
$|p|\geq 2$,  $\mathfrak {h}^{p,-p} = \mathfrak {g}^{p,-p}$ and there exists an abelian subalgebra
$\mathfrak {h}^{p,-p} = \mathfrak {g}^{p,-p}$ and there exists an abelian subalgebra  $\mathfrak {a} \subset \mathfrak {g}^{-1,1}$ such that
$\mathfrak {a} \subset \mathfrak {g}^{-1,1}$ such that
 \[ \mathfrak a + \mathfrak{h}^{-1,1} = \mathfrak{g}^{-1,1}. \]
\[ \mathfrak a + \mathfrak{h}^{-1,1} = \mathfrak{g}^{-1,1}. \]
Proof. Assume that there exists a smooth variation of Hodge structure ![]() $X\subset G/K$ which is generically transverse to
$X\subset G/K$ which is generically transverse to ![]() $H/L$. Up to left multiplication by some
$H/L$. Up to left multiplication by some ![]() $g\in G$, we can assume that
$g\in G$, we can assume that ![]() $x\in X$ and that
$x\in X$ and that
Now, because ![]() $X$ is a variation of Hodge structure,
$X$ is a variation of Hodge structure, ![]() $T_x^{1,0} X$ is an abelian subalgebra of
$T_x^{1,0} X$ is an abelian subalgebra of ![]() $\mathfrak {g}^{-1,1}$, whereas
$\mathfrak {g}^{-1,1}$, whereas ![]() $T_w^{1,0}H/L = \bigoplus _{p<0} \mathfrak {h}^{p,-p}$. The identity (5.2.1) thus implies that
$T_w^{1,0}H/L = \bigoplus _{p<0} \mathfrak {h}^{p,-p}$. The identity (5.2.1) thus implies that
and
for all ![]() $p\geq 2$, and by Hodge symmetry, also for
$p\geq 2$, and by Hodge symmetry, also for ![]() $p\leq -2$.
$p\leq -2$.
Conversely, assume ![]() $\mathfrak {h}^{-p,p} = \mathfrak {g}^{-p,p}$ for all
$\mathfrak {h}^{-p,p} = \mathfrak {g}^{-p,p}$ for all ![]() $p\geq 2$ and
$p\geq 2$ and ![]() $\mathfrak a^{-1,1} + \mathfrak {h}^{-1,1} = \mathfrak {g}^{-1,1}$ for some abelian Lie subalgebra
$\mathfrak a^{-1,1} + \mathfrak {h}^{-1,1} = \mathfrak {g}^{-1,1}$ for some abelian Lie subalgebra ![]() $\mathfrak a$. Let
$\mathfrak a$. Let ![]() $A$ denote the complex abelian subgroup of
$A$ denote the complex abelian subgroup of ![]() $G_\mathbb {C}$ spanned by
$G_\mathbb {C}$ spanned by ![]() $\mathfrak a$. Recall that
$\mathfrak a$. Recall that ![]() $G_\mathbb {C}$ acts on the compactified period domain
$G_\mathbb {C}$ acts on the compactified period domain ![]() $\bar { \mathcal {D} }$. If
$\bar { \mathcal {D} }$. If ![]() $U$ is a sufficiently small neighborhood of the identity in
$U$ is a sufficiently small neighborhood of the identity in ![]() $A$, then
$A$, then
is a smooth holomorphic submanifold contained in ![]() $\mathcal {D}$. As
$\mathcal {D}$. As ![]() $\mathfrak a \subset \mathfrak {g}^{-1,1}$ and
$\mathfrak a \subset \mathfrak {g}^{-1,1}$ and ![]() $A$ is abelian,
$A$ is abelian, ![]() $X$ is tangent to the Griffith distribution at every point. Hence,
$X$ is tangent to the Griffith distribution at every point. Hence, ![]() $X$ is a smooth variation of Hodge structure transverse to
$X$ is a smooth variation of Hodge structure transverse to ![]() $H/L$ at
$H/L$ at ![]() $x$.
$x$.
Remark 5.12 Baldi, Klingler, and Ullmo [Reference Baldi, Klingler and UllmoBKU21, Prop. 6.5] proved that, when ![]() $\mathfrak {g}$ is simple and has components
$\mathfrak {g}$ is simple and has components ![]() $\mathfrak {g}^{k,-k}$ for
$\mathfrak {g}^{k,-k}$ for ![]() $k\geq 3$, then a Lie subalgebra
$k\geq 3$, then a Lie subalgebra ![]() $\mathfrak {h}$ can never contain
$\mathfrak {h}$ can never contain ![]() $\mathfrak {g}^{k,-k}$,
$\mathfrak {g}^{k,-k}$, ![]() $k\geq 3$. It follows that the transverse Hodge locus is always empty in that case.
$k\geq 3$. It follows that the transverse Hodge locus is always empty in that case.
5.3 Chern classes of the Hodge bundles
Let ![]() $\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a variation of Hodge structure of weight
$\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a variation of Hodge structure of weight ![]() $k$ over a complex analytic variety
$k$ over a complex analytic variety ![]() $X$. Let
$X$. Let ![]() $\sigma$ be the antilinear automorphism of
$\sigma$ be the antilinear automorphism of ![]() $\mathcal {V}$ given by
$\mathcal {V}$ given by
and let ![]() $h$ be the Hermitian form
$h$ be the Hermitian form
By the definition of Hodge structures, ![]() $h$ is positive-definite and the decomposition
$h$ is positive-definite and the decomposition
is orthogonal for ![]() $h$.
$h$.
We have ![]() $\sigma ^2= (-1)^k \mathrm {Id}_{\mathcal {V}}$. Define now a new linear connection
$\sigma ^2= (-1)^k \mathrm {Id}_{\mathcal {V}}$. Define now a new linear connection ![]() $\nabla _h$ on
$\nabla _h$ on ![]() $\mathcal {V}$ by
$\mathcal {V}$ by
(The connection ![]() $\nabla _h$ is the part of the connection
$\nabla _h$ is the part of the connection ![]() $\nabla$ that preserves
$\nabla$ that preserves ![]() $\sigma$.) Then
$\sigma$.) Then ![]() $\nabla _h$ preserves the metric
$\nabla _h$ preserves the metric ![]() $h$ and the orthogonal decomposition
$h$ and the orthogonal decomposition
Let ![]() ${\nabla _h}^{p,q}$ denote the induced Hermitian connection on
${\nabla _h}^{p,q}$ denote the induced Hermitian connection on ![]() $\mathcal {V}^{p,q}$. and
$\mathcal {V}^{p,q}$. and ![]() $\Theta _h^{p,q}$ denotes its curvature. One can show that
$\Theta _h^{p,q}$ denotes its curvature. One can show that ![]() $\Theta _h^{p,q}$ is of type
$\Theta _h^{p,q}$ is of type ![]() $(1,1)$.
$(1,1)$.
Definition 5.13 The Chern forms of ![]() $\mathcal {V}^{p,q}$ are the
$\mathcal {V}^{p,q}$ are the ![]() $(\ell,\ell )$ forms
$(\ell,\ell )$ forms ![]() $c_\ell (\mathcal {V}^{p,q})$,
$c_\ell (\mathcal {V}^{p,q})$, ![]() $1\leq l \leq h^{p,q}$ defined by
$1\leq l \leq h^{p,q}$ defined by
 \[ \det\biggl(\mathrm{I}_{\mathcal{V}^{p,q}}+\frac{i}{2\pi} \Theta_h^{p,q}\biggr)=1+ \sum_{\ell=1}^{h^{p,q}} c_\ell(\mathcal{V}^{p,q}). \]
\[ \det\biggl(\mathrm{I}_{\mathcal{V}^{p,q}}+\frac{i}{2\pi} \Theta_h^{p,q}\biggr)=1+ \sum_{\ell=1}^{h^{p,q}} c_\ell(\mathcal{V}^{p,q}). \]
It is well-known that the form ![]() $c_\ell (\mathcal {V}^{p,q})$ represents the
$c_\ell (\mathcal {V}^{p,q})$ represents the ![]() $\ell$th Chern class of
$\ell$th Chern class of ![]() $\mathcal {V}^{p,q}$ in de Rham cohomology of
$\mathcal {V}^{p,q}$ in de Rham cohomology of ![]() $X$.
$X$.
These Chern forms turn out to be pull-backs of invariant forms under the period map. Indeed, ![]() $\sigma$,
$\sigma$, ![]() $h$, and
$h$, and ![]() $\nabla _h$ can be defined on the universal Hodge decomposition
$\nabla _h$ can be defined on the universal Hodge decomposition
 \[ \mathcal{U} = \bigoplus_{p=0}^k \mathcal{U}^{p,q} \]
\[ \mathcal{U} = \bigoplus_{p=0}^k \mathcal{U}^{p,q} \]
over ![]() $\mathcal {D}$. There, these objects are
$\mathcal {D}$. There, these objects are ![]() $G$-equivariant and induce
$G$-equivariant and induce ![]() $G$-invariant Chern forms
$G$-invariant Chern forms ![]() $c_\ell (\mathcal {U}^{p,q})$. These factor to the quotient
$c_\ell (\mathcal {U}^{p,q})$. These factor to the quotient ![]() $G_\mathbb {Z}\backslash \mathcal {D}$ and, if
$G_\mathbb {Z}\backslash \mathcal {D}$ and, if ![]() $f: X \to G_\mathbb {Z}\backslash \mathcal {D}$ denotes the period map, we have
$f: X \to G_\mathbb {Z}\backslash \mathcal {D}$ denotes the period map, we have
5.3.1 Expression at the Lie algebra level
Let us now express the Chern forms ![]() $c_\ell (\mathcal {U}^{p,q})$ at the Lie algebra level.
$c_\ell (\mathcal {U}^{p,q})$ at the Lie algebra level.
Let us fix a basepoint ![]() $o$ in
$o$ in ![]() $\mathcal {D}$ with stabilizer
$\mathcal {D}$ with stabilizer ![]() $K$. The group
$K$. The group ![]() $K$ decomposes as
$K$ decomposes as
 \[ K = \prod_{p=1}^{\lfloor{k}/{2}\rfloor}K^{p,q}, \]
\[ K = \prod_{p=1}^{\lfloor{k}/{2}\rfloor}K^{p,q}, \]
where ![]() $K^{p,q} \simeq \mathrm U(h^{p,q})$ for
$K^{p,q} \simeq \mathrm U(h^{p,q})$ for ![]() $p>q$ and
$p>q$ and ![]() $K^{k',k'} \simeq \mathrm {O}(h^{k',k'})$ when
$K^{k',k'} \simeq \mathrm {O}(h^{k',k'})$ when ![]() $k= 2k'$ is even.
$k= 2k'$ is even.
When ![]() $p\geq q$ (respectively,
$p\geq q$ (respectively, ![]() $p\leq q$), the bundle
$p\leq q$), the bundle ![]() $\mathcal {U}^{p,q}$ is the bundle associated with the linear representation of
$\mathcal {U}^{p,q}$ is the bundle associated with the linear representation of ![]() $K$ that factors through the standard representation of
$K$ that factors through the standard representation of ![]() $K^{p,q}$ (respectively, the dual representation). Let
$K^{p,q}$ (respectively, the dual representation). Let ![]() $\mathfrak {k}^{p,q}$ denote the Lie algebra of
$\mathfrak {k}^{p,q}$ denote the Lie algebra of ![]() $K^{p,q}$. Then, for
$K^{p,q}$. Then, for ![]() $p\geq q$, the curvature of
$p\geq q$, the curvature of ![]() $\mathcal {U}^{p,q}$ at
$\mathcal {U}^{p,q}$ at ![]() $x$ is the
$x$ is the ![]() $2$-form on
$2$-form on ![]() $\mathfrak {g}/\mathfrak {k}$ with values in
$\mathfrak {g}/\mathfrak {k}$ with values in ![]() $\mathfrak {k}^{p,q}\subset \operatorname {End}(\mathcal {U}^{p,q})$ given by
$\mathfrak {k}^{p,q}\subset \operatorname {End}(\mathcal {U}^{p,q})$ given by
where ![]() $\pi _{p,q}: \mathfrak {g} \to \mathfrak {k}^{p,q}$ denotes the orthogonal projection for the Killing metric.
$\pi _{p,q}: \mathfrak {g} \to \mathfrak {k}^{p,q}$ denotes the orthogonal projection for the Killing metric.
5.3.2 Chern forms on the compact dual
Recall from § 4.3 that we have an isomorphism of differential algebras
which consists in identifying both spaces with ![]() $\Lambda _\mathbb {C}^\bullet (\mathfrak {g}_\mathbb {C}/\mathfrak {k}_\mathbb {C})^{K_\mathbb {C}}$.
$\Lambda _\mathbb {C}^\bullet (\mathfrak {g}_\mathbb {C}/\mathfrak {k}_\mathbb {C})^{K_\mathbb {C}}$.
We now wish to identify the invariant forms on ![]() $G_U/K$ corresponding to the Chern forms on
$G_U/K$ corresponding to the Chern forms on ![]() $G/K$.
$G/K$.
Recall that ![]() $\widehat {\mathcal {D}}= G_\mathbb {C}/P$ is the space of complex flags
$\widehat {\mathcal {D}}= G_\mathbb {C}/P$ is the space of complex flags
such that
(where the orthogonal is intended with respect to the bilinear form ![]() $B$) and
$B$) and
Let ![]() $\widehat {\mathcal {U}}$ denote the trivial bundle over
$\widehat {\mathcal {U}}$ denote the trivial bundle over ![]() $\widehat {\mathcal {D}}$ equipped with the action of
$\widehat {\mathcal {D}}$ equipped with the action of ![]() $G_\mathbb {C}$ given by the standard linear action in the fibers. The bundle
$G_\mathbb {C}$ given by the standard linear action in the fibers. The bundle ![]() $\widehat {\mathcal {U}}$ admits a tautological filtration
$\widehat {\mathcal {U}}$ admits a tautological filtration ![]() $\mathcal {F}^\bullet \widehat {\mathcal {U}}$ by
$\mathcal {F}^\bullet \widehat {\mathcal {U}}$ by ![]() $G_\mathbb {C}$-equivariant vector bundles which is given at a point
$G_\mathbb {C}$-equivariant vector bundles which is given at a point ![]() $x$ by the flag defining
$x$ by the flag defining ![]() $x$.
$x$.
By construction, the restriction of ![]() $\mathcal {F}^\bullet \widehat {\mathcal {U}}$ to the open domain
$\mathcal {F}^\bullet \widehat {\mathcal {U}}$ to the open domain ![]() $\mathcal {D}$ is the filtration
$\mathcal {D}$ is the filtration ![]() $\mathcal {F}^\bullet \mathcal {U}$ of
$\mathcal {F}^\bullet \mathcal {U}$ of ![]() $\mathcal {U}$ given (in
$\mathcal {U}$ given (in ![]() $C^\infty$) by
$C^\infty$) by
Let us now prove that the dual space ![]() $G_U/K$ identifies with
$G_U/K$ identifies with ![]() $\widehat {\mathcal {D}}$.
$\widehat {\mathcal {D}}$.
Proposition 5.14 The group ![]() $G_U$ is (conjugated to) the subgroup of
$G_U$ is (conjugated to) the subgroup of ![]() $G_\mathbb {C} = \operatorname {Aut}_\mathbb {C}(B)$ commuting with the antilinear automorphism
$G_\mathbb {C} = \operatorname {Aut}_\mathbb {C}(B)$ commuting with the antilinear automorphism ![]() $\sigma$.
$\sigma$.
Proof. Let ![]() $\tau : \mathcal {V}_o \to \mathcal {V}_o$ be the complex conjugation and
$\tau : \mathcal {V}_o \to \mathcal {V}_o$ be the complex conjugation and ![]() $\theta = \sigma \tau$. Conjugation by
$\theta = \sigma \tau$. Conjugation by ![]() $\tau$ is the anti-holomorphic involution of
$\tau$ is the anti-holomorphic involution of ![]() $G_\mathbb {C}$ fixing
$G_\mathbb {C}$ fixing ![]() $G$ and one verifies that the conjugation with
$G$ and one verifies that the conjugation with ![]() $\sigma \tau$ is a Cartan involution of
$\sigma \tau$ is a Cartan involution of ![]() $G$ fixing
$G$ fixing ![]() $K$. With respect to this choice of Cartan involution, the group
$K$. With respect to this choice of Cartan involution, the group ![]() $G_U$ is then the fixed point set of conjugation by
$G_U$ is then the fixed point set of conjugation by ![]() $\sigma$.
$\sigma$.
Corollary 5.15 The group ![]() $G_U$ acts transitively on
$G_U$ acts transitively on ![]() $\widehat {\mathcal {D}}$, and the stabilizer of
$\widehat {\mathcal {D}}$, and the stabilizer of ![]() $o$ in
$o$ in ![]() $G_U$ is
$G_U$ is ![]() $K$.
$K$.
Proof. As a maximal compact subgroup of ![]() $G_\mathbb {C}$, the group
$G_\mathbb {C}$, the group ![]() $G_U$ acts transitively on the flag variety
$G_U$ acts transitively on the flag variety ![]() $\widehat {\mathcal {D}}$, and the stabilizer
$\widehat {\mathcal {D}}$, and the stabilizer ![]() $K'$ of
$K'$ of ![]() $o$ preserves the flag
$o$ preserves the flag ![]() $\mathcal {F}^\bullet \mathcal {U}_o$. Now, because
$\mathcal {F}^\bullet \mathcal {U}_o$. Now, because ![]() $G_U$ commutes with
$G_U$ commutes with ![]() $\sigma$, it preserves the Hermitian form
$\sigma$, it preserves the Hermitian form ![]() $B(\cdot, \sigma \cdot )$. Therefore,
$B(\cdot, \sigma \cdot )$. Therefore, ![]() $K'$ preserves the orthogonal of
$K'$ preserves the orthogonal of ![]() $\mathcal {F}^{p+1} \mathcal {U}_o$ in
$\mathcal {F}^{p+1} \mathcal {U}_o$ in ![]() $\mathcal {F}^p \mathcal {U}_o$ for
$\mathcal {F}^p \mathcal {U}_o$ for ![]() $B(\cdot, \sigma \cdot )$, which is precisely
$B(\cdot, \sigma \cdot )$, which is precisely ![]() $\mathcal {U}^{p,q}$. We conclude that
$\mathcal {U}^{p,q}$. We conclude that ![]() $K= K'$.
$K= K'$.
The ![]() $G_U$-invariant form
$G_U$-invariant form ![]() $B(\cdot, \sigma \cdot )$ induces a flat
$B(\cdot, \sigma \cdot )$ induces a flat ![]() $G_U$-invariant Hermitian metric
$G_U$-invariant Hermitian metric ![]() $\widehat {h}$ on
$\widehat {h}$ on ![]() $\widehat {\mathcal {U}}$. Let
$\widehat {\mathcal {U}}$. Let ![]() $\widehat {\mathcal {U}}^{p,q}$ denote the
$\widehat {\mathcal {U}}^{p,q}$ denote the ![]() $\widehat {h}$-orthogonal of
$\widehat {h}$-orthogonal of ![]() $\mathcal {F}^{p+1}\widehat {\mathcal {U}}$ in
$\mathcal {F}^{p+1}\widehat {\mathcal {U}}$ in ![]() $\mathcal {F}$. Then the bundle
$\mathcal {F}$. Then the bundle ![]() $\widehat {\mathcal {U}}^{p,q}$ is
$\widehat {\mathcal {U}}^{p,q}$ is ![]() $G_U$-invariant and carries a
$G_U$-invariant and carries a ![]() $G_U$-invariant Hermitian connection
$G_U$-invariant Hermitian connection ![]() $\nabla _{\widehat {h}}^{p,q}$ with curvature form
$\nabla _{\widehat {h}}^{p,q}$ with curvature form ![]() $\Theta _{\widehat {h}}^{p,q}$. The Chern forms of this connection define
$\Theta _{\widehat {h}}^{p,q}$. The Chern forms of this connection define ![]() $G_U$-invariant forms
$G_U$-invariant forms
which represent the Chern classes of ![]() $\widehat {\mathcal {U}}^{p,q} \simeq \mathcal {F}^p\widehat {\mathcal {U}}/\mathcal {F}^{p+1} \widehat {U}$ on
$\widehat {\mathcal {U}}^{p,q} \simeq \mathcal {F}^p\widehat {\mathcal {U}}/\mathcal {F}^{p+1} \widehat {U}$ on ![]() $\widehat {\mathcal {D}}$.
$\widehat {\mathcal {D}}$.
Proposition 5.16 The isomorphism ![]() $\phi :\Omega ^{2l}(G/K,\mathbb {C})^G\to \Omega ^{2l}(G_U/K,\mathbb {C})^G$ maps
$\phi :\Omega ^{2l}(G/K,\mathbb {C})^G\to \Omega ^{2l}(G_U/K,\mathbb {C})^G$ maps ![]() $c_\ell (\mathcal {U}^{p,q})$ to
$c_\ell (\mathcal {U}^{p,q})$ to ![]() $c_\ell (\widehat {\mathcal {U}}^{p,q}) \in \Omega ^{2l}(G_U/K,\mathbb {C})^G$.
$c_\ell (\widehat {\mathcal {U}}^{p,q}) \in \Omega ^{2l}(G_U/K,\mathbb {C})^G$.
Remark 5.17 The isomorphism ![]() $\phi$ is not induced by the identification
$\phi$ is not induced by the identification
coming from the inclusion ![]() $\mathcal {D}\subset \widehat { \mathcal {D}}$ but rather from the diagram in Proposition 4.7.
$\mathcal {D}\subset \widehat { \mathcal {D}}$ but rather from the diagram in Proposition 4.7.
Proof. For ![]() $p\geq q$, the bundle
$p\geq q$, the bundle ![]() $\widehat {\mathcal {U}}^{p,q}$ is the vector bundle on
$\widehat {\mathcal {U}}^{p,q}$ is the vector bundle on ![]() $G_U/K$ associated with the linear representation of
$G_U/K$ associated with the linear representation of ![]() $K$ factoring through the standard representation of
$K$ factoring through the standard representation of ![]() $K^{p,q}$. Hence, its curvature form at
$K^{p,q}$. Hence, its curvature form at ![]() $o$ is given by a formula similar to § 5.3.1.
$o$ is given by a formula similar to § 5.3.1.
Now let ![]() $\pi ^{p,q}_\mathbb {C}$ denote the orthogonal projection of
$\pi ^{p,q}_\mathbb {C}$ denote the orthogonal projection of ![]() $\mathfrak {g}_\mathbb {C}$ to
$\mathfrak {g}_\mathbb {C}$ to ![]() $\mathfrak {k}_\mathbb {C}^{p,q}$ for the complex Killing form. Then
$\mathfrak {k}_\mathbb {C}^{p,q}$ for the complex Killing form. Then ![]() $\pi ^{p,q}_\mathbb {C}$ restricts to the orthogonal projection to
$\pi ^{p,q}_\mathbb {C}$ restricts to the orthogonal projection to ![]() $\mathfrak {k}$ on both
$\mathfrak {k}$ on both ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\mathfrak {g}_U$.
$\mathfrak {g}_U$.
Therefore, both the curvature forms of ![]() $\mathcal {U}^{p,q}$ and
$\mathcal {U}^{p,q}$ and ![]() $\widehat {\mathcal {U}}^{p,q}$ at
$\widehat {\mathcal {U}}^{p,q}$ at ![]() $o$ are given by
$o$ are given by
hence all the symmetric polynomials in those curvature forms are identified by ![]() $\phi$.
$\phi$.
5.3.3 Characteristic cohomology
As mentioned in § 4.3.1, there might be ![]() $G$-invariant forms on
$G$-invariant forms on ![]() $\mathcal {D}$ which are not closed, in which case
$\mathcal {D}$ which are not closed, in which case ![]() $G$-invariant closed forms are not characterized by the corresponding cohomology class in
$G$-invariant closed forms are not characterized by the corresponding cohomology class in ![]() $\mathrm H^\bullet (\widehat {\mathcal {D}})$.
$\mathrm H^\bullet (\widehat {\mathcal {D}})$.
In the context of variations of Hodge structure, however, we are ultimately interested in the restriction of ![]() $G$-invariant forms to submanifolds that are tangent to the Griffiths’ distribution. This motivates the introduction of the characteristic cohomology of a period domain, which, roughly speaking, restricts the differential algebra of invariant forms to the Griffiths’ distribution (see [Reference Green, Griffiths and KerrGGK10, III.A]).
$G$-invariant forms to submanifolds that are tangent to the Griffiths’ distribution. This motivates the introduction of the characteristic cohomology of a period domain, which, roughly speaking, restricts the differential algebra of invariant forms to the Griffiths’ distribution (see [Reference Green, Griffiths and KerrGGK10, III.A]).
We do not define this notion here and only mention the analogous of Cartan's theorem, which comforts the idea that the geometry of period domains is similar to that of symmetric spaces ‘in restriction to the Griffiths’ distribution’.
Proposition 5.18 Let ![]() $X$ be a complex manifold and
$X$ be a complex manifold and ![]() $f:\widetilde {X} \to G/K$ the period map of a variation of Hodge structure. Then, for every
$f:\widetilde {X} \to G/K$ the period map of a variation of Hodge structure. Then, for every ![]() $\alpha \in \Omega ^\bullet (G/K,\mathbb {C})^G$, the pull-back form
$\alpha \in \Omega ^\bullet (G/K,\mathbb {C})^G$, the pull-back form ![]() $f^*\alpha$ is closed of bidegree
$f^*\alpha$ is closed of bidegree ![]() $(p,p)$ for some
$(p,p)$ for some ![]() $p$.
$p$.
Proof. Let ![]() $\alpha$ be a
$\alpha$ be a ![]() $G$-invariant form on
$G$-invariant form on ![]() $G/K$. Let
$G/K$. Let ![]() $x$ be a point in
$x$ be a point in ![]() $X$ and
$X$ and ![]() $\varphi : \mathbb {C}^\times \to G_\mathbb {R}$ the representation of the Deligne torus defining the Hodge structure
$\varphi : \mathbb {C}^\times \to G_\mathbb {R}$ the representation of the Deligne torus defining the Hodge structure ![]() $f(x)$. Then
$f(x)$. Then ![]() $\varphi (\mathbb {U}^1)$ is a subgroup of
$\varphi (\mathbb {U}^1)$ is a subgroup of ![]() $\mathrm {Stab}(x)\subset G$ and acts on
$\mathrm {Stab}(x)\subset G$ and acts on ![]() $W^{-1,0}$ by complex multiplication, where
$W^{-1,0}$ by complex multiplication, where ![]() $W$ is the tangent space at
$W$ is the tangent space at ![]() $f(x)$. As
$f(x)$. As ![]() ${\alpha _{f(x)}}$ is
${\alpha _{f(x)}}$ is ![]() $\varphi (\mathbb {U}^1)$-invariant, it must belong to
$\varphi (\mathbb {U}^1)$-invariant, it must belong to ![]() $\Lambda ^{p,p}(W_x^*)$ for some
$\Lambda ^{p,p}(W_x^*)$ for some ![]() $p$, and we conclude that
$p$, and we conclude that ![]() $f^*\alpha$ has bidegree
$f^*\alpha$ has bidegree ![]() $(p,p)$ because
$(p,p)$ because ![]() $f$ is holomorphic. In particular,
$f$ is holomorphic. In particular, ![]() $f^*\alpha$ has even degree.
$f^*\alpha$ has even degree.
Now, ![]() $d\alpha$ is also a
$d\alpha$ is also a ![]() $G$-invariant form and
$G$-invariant form and ![]() $f^*(d \alpha ) = d(f^*\alpha )$ has odd degree. By the previous argument, it must vanish.
$f^*(d \alpha ) = d(f^*\alpha )$ has odd degree. By the previous argument, it must vanish.
Corollary 5.19 Let ![]() $\alpha$ be a closed invariant form on
$\alpha$ be a closed invariant form on ![]() $\mathcal {D}$. Then the pullback of
$\mathcal {D}$. Then the pullback of ![]() $\alpha$ by any variation of Hodge structure is completely determined by the cohomology class
$\alpha$ by any variation of Hodge structure is completely determined by the cohomology class ![]() $[\phi (\alpha )]\in \mathrm H^\bullet (\widehat {\mathcal {D}})$.
$[\phi (\alpha )]\in \mathrm H^\bullet (\widehat {\mathcal {D}})$.
Proof. Let ![]() $\alpha '$ be another closed
$\alpha '$ be another closed ![]() $G$-invariant form on
$G$-invariant form on ![]() $G/K$ such that
$G/K$ such that ![]() $\phi (\alpha - \alpha ')$ is exact on
$\phi (\alpha - \alpha ')$ is exact on ![]() $G_U/K$. We can write
$G_U/K$. We can write ![]() $\alpha -\alpha '= d \beta$, where
$\alpha -\alpha '= d \beta$, where ![]() $\beta$ is
$\beta$ is ![]() $G$-invariant. Now let
$G$-invariant. Now let ![]() $f:X\to G/K$ be a variation of Hodge structure. Then
$f:X\to G/K$ be a variation of Hodge structure. Then ![]() $f^*\beta$ is closed by the previous proposition, hence
$f^*\beta$ is closed by the previous proposition, hence
Remark 5.20 We only mentioned these results for period domains, but one can prove that they remain true on every Mumford–Tate domain.
5.4 Examples
We now apply the previous considerations to compute the pull–push form in various examples.
5.4.1 Noether–Lefschetz loci in weight two
Assume in this section that ![]() $\mathcal {D}$ is the period domain for a polarized variation of Hodge structure of weight two on a quadratic lattice
$\mathcal {D}$ is the period domain for a polarized variation of Hodge structure of weight two on a quadratic lattice ![]() $(V,B)$ which is assumed to be of signature
$(V,B)$ which is assumed to be of signature ![]() $(p,2q)$. Let
$(p,2q)$. Let ![]() $R$ be a rational subspace of
$R$ be a rational subspace of ![]() $V \otimes _\mathbb {Z} \mathbb {Q}$ of rank
$V \otimes _\mathbb {Z} \mathbb {Q}$ of rank ![]() $r\leq h^{1,1}$ such that
$r\leq h^{1,1}$ such that ![]() $B$ is positive-definite in restriction to
$B$ is positive-definite in restriction to ![]() $R\otimes _\mathbb {Q} \mathbb {R}$, and let
$R\otimes _\mathbb {Q} \mathbb {R}$, and let ![]() $\mathcal {D}_R \subset \mathcal {D}$ be the set of Hodge structures
$\mathcal {D}_R \subset \mathcal {D}$ be the set of Hodge structures ![]() $x\in \mathcal {D}$ such that
$x\in \mathcal {D}$ such that ![]() $R\subset \mathcal {V}^{1,1}_x$.
$R\subset \mathcal {V}^{1,1}_x$.
Choose a basepoint ![]() $o$ in
$o$ in ![]() $\mathcal {D}_R$. Let
$\mathcal {D}_R$. Let ![]() $K$ be the stabilizer of
$K$ be the stabilizer of ![]() $o$ in
$o$ in ![]() $G$, let
$G$, let ![]() $H$ be the subgroup of
$H$ be the subgroup of ![]() $G$ fixing
$G$ fixing ![]() $R$, and
$R$, and ![]() $L=K\cap H$. Then
$L=K\cap H$. Then ![]() $H$ is a Mumford–Tate group and
$H$ is a Mumford–Tate group and ![]() $\mathcal {D}_R \subset \mathcal {D}$ is the Mumford–Tate domain
$\mathcal {D}_R \subset \mathcal {D}$ is the Mumford–Tate domain ![]() $H/L\subset G/K$.
$H/L\subset G/K$.
Denoting as before by ![]() $p$ and
$p$ and ![]() $\pi$ the respective projections from
$\pi$ the respective projections from ![]() $G/L$ to
$G/L$ to ![]() $G/H$ and
$G/H$ and ![]() $G/K$, we can now prove the following.
$G/K$, we can now prove the following.
Theorem 5.21 Let ![]() $X$ be an smooth complex analytic manifold, let
$X$ be an smooth complex analytic manifold, let ![]() $\mathcal {V} = \mathcal {V}^{2,0} \oplus \mathcal {V}^{1,1} \oplus \mathcal {V}^{0,2}$ be the
$\mathcal {V} = \mathcal {V}^{2,0} \oplus \mathcal {V}^{1,1} \oplus \mathcal {V}^{0,2}$ be the ![]() $C^\infty$ Hodge decomposition of a variation of Hodge structure of weight two and Hodge numbers
$C^\infty$ Hodge decomposition of a variation of Hodge structure of weight two and Hodge numbers ![]() $(q,p,q)$ on
$(q,p,q)$ on ![]() $X$ and let
$X$ and let ![]() $\widetilde {f}:\widetilde {X} \to \mathcal {D}$ be the corresponding period map. Then
$\widetilde {f}:\widetilde {X} \to \mathcal {D}$ be the corresponding period map. Then
Proof. Let ![]() $\sigma$ be the antilinear automorphism defined in the previous section. As we are in even weight,
$\sigma$ be the antilinear automorphism defined in the previous section. As we are in even weight, ![]() $\sigma$ is an involution which fixes a real form
$\sigma$ is an involution which fixes a real form ![]() $\mathcal {U}^\sigma$ of
$\mathcal {U}^\sigma$ of ![]() $\mathcal {U}_o$ on which the symmetric form
$\mathcal {U}_o$ on which the symmetric form ![]() $B$ is real and positive-definite. As
$B$ is real and positive-definite. As ![]() $\sigma$ coincides with the standard complex conjugation on
$\sigma$ coincides with the standard complex conjugation on ![]() $\mathcal {U}^{1,1}_o$, the subspace
$\mathcal {U}^{1,1}_o$, the subspace ![]() $R$ is contained in
$R$ is contained in ![]() $\mathcal {U}^\sigma$.
$\mathcal {U}^\sigma$.
Now, ![]() $G_U$ is the subgroup of
$G_U$ is the subgroup of ![]() $G_\mathbb {C} = \operatorname {Aut}_\mathbb {C}(B)$ preserving
$G_\mathbb {C} = \operatorname {Aut}_\mathbb {C}(B)$ preserving ![]() $\mathcal {U}^\sigma$ and
$\mathcal {U}^\sigma$ and ![]() $H_U= G_U\cap H_\mathbb {C}$ is the subgroup of
$H_U= G_U\cap H_\mathbb {C}$ is the subgroup of ![]() $G_U$ fixing
$G_U$ fixing ![]() $R$. Therefore,
$R$. Therefore, ![]() $H_U/L$ is the domain
$H_U/L$ is the domain ![]() $\widehat {\mathcal {D}}_R \subset \widehat {\mathcal {D}}$ where
$\widehat {\mathcal {D}}_R \subset \widehat {\mathcal {D}}$ where ![]() $\widehat {\mathcal {U}}^{1,1}$ contains
$\widehat {\mathcal {U}}^{1,1}$ contains ![]() $R$. As
$R$. As ![]() $R$ is
$R$ is ![]() $\sigma$-invariant and
$\sigma$-invariant and
we also have that
Let ![]() $(u_1,\ldots, u_r)$ be a basis of
$(u_1,\ldots, u_r)$ be a basis of ![]() $R$. The projection of
$R$. The projection of ![]() $u_\ell$ into
$u_\ell$ into ![]() $\mathcal {F}^0\widehat {\mathcal {U}}/\mathcal {F}^1 \widehat {\mathcal {U}}$ defines a holomorphic section
$\mathcal {F}^0\widehat {\mathcal {U}}/\mathcal {F}^1 \widehat {\mathcal {U}}$ defines a holomorphic section ![]() $s_\ell$ of
$s_\ell$ of ![]() $\mathcal {F}^0\widehat {\mathcal {U}}/\mathcal {F}^1 \widehat {\mathcal {U}}$, and
$\mathcal {F}^0\widehat {\mathcal {U}}/\mathcal {F}^1 \widehat {\mathcal {U}}$, and ![]() $\widehat {\mathcal {D}}_R$ is the transverse intersection of the vanishing loci of all the
$\widehat {\mathcal {D}}_R$ is the transverse intersection of the vanishing loci of all the ![]() $s_\ell$. We conclude that
$s_\ell$. We conclude that ![]() $\widehat {\mathcal {D}}_R$ is Poincaré dual to the
$\widehat {\mathcal {D}}_R$ is Poincaré dual to the ![]() $r$th power of the Euler class of
$r$th power of the Euler class of ![]() $\mathcal {F}^0\widehat {\mathcal {U}}/\mathcal {F}^1\widehat {\mathcal {U}}$, i.e.
$\mathcal {F}^0\widehat {\mathcal {U}}/\mathcal {F}^1\widehat {\mathcal {U}}$, i.e.
By Lemma 4.9, we have
for some invariant form ![]() $\alpha$.
$\alpha$.
By Corollary 4.8 and Proposition 5.16 we have
 \begin{align*} \pi_*p^*\omega_{G/H} &= i^{2qr} \pi_*p^*\omega_{G_U/H_U}\\ &= (-1)^{qr}c_q(\widehat{\mathcal{U}}^{0,2})^r + (-1)^{qr}\,{d} \alpha\\ &= c_q(\widehat{\mathcal{U}}^{2,0})^r + (-1)^{qr}\,{d} \alpha\\ &= c_q(\mathcal{U}^{2,0})^r + (-1)^{qr} \,{d} \alpha. \end{align*}
\begin{align*} \pi_*p^*\omega_{G/H} &= i^{2qr} \pi_*p^*\omega_{G_U/H_U}\\ &= (-1)^{qr}c_q(\widehat{\mathcal{U}}^{0,2})^r + (-1)^{qr}\,{d} \alpha\\ &= c_q(\widehat{\mathcal{U}}^{2,0})^r + (-1)^{qr}\,{d} \alpha\\ &= c_q(\mathcal{U}^{2,0})^r + (-1)^{qr} \,{d} \alpha. \end{align*}
Finally, by Proposition 5.18, the pull-back of ![]() ${d} \alpha$ by the period map of a variation of Hodge structure vanishes, and the conclusion follows.
${d} \alpha$ by the period map of a variation of Hodge structure vanishes, and the conclusion follows.
5.4.2 Diagonal embedding of Shimura varieties
Let ![]() $G_1$ be a semi-simple Lie group of Hermitian type and let
$G_1$ be a semi-simple Lie group of Hermitian type and let ![]() $K_1$ be a maximal compact subgroup, so that
$K_1$ be a maximal compact subgroup, so that ![]() $\mathcal {D} \overset {\text {def}}= G_1/K_1$ is a Hermitian symmetric space of non-compact type. We apply the results of previous sections to
$\mathcal {D} \overset {\text {def}}= G_1/K_1$ is a Hermitian symmetric space of non-compact type. We apply the results of previous sections to ![]() $G=G_1\times G_1$ and
$G=G_1\times G_1$ and ![]() $H=\Delta (G_1)$, the diagonal embedding of
$H=\Delta (G_1)$, the diagonal embedding of ![]() $G_1$. Let
$G_1$. Let ![]() $\Delta : \mathcal {D}\hookrightarrow \mathcal {D}\times \mathcal {D}$ be the corresponding diagonal embedding of symmetric spaces.
$\Delta : \mathcal {D}\hookrightarrow \mathcal {D}\times \mathcal {D}$ be the corresponding diagonal embedding of symmetric spaces.
First, recall that because ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {D}\times \mathcal {D}$ are Hermitian symmetric, their tangent space is equal to the Griffiths’ distribution. Hence, by Proposition 5.18, the complex
$\mathcal {D}\times \mathcal {D}$ are Hermitian symmetric, their tangent space is equal to the Griffiths’ distribution. Hence, by Proposition 5.18, the complex ![]() $\Omega ^\bullet (\mathcal {D}\times \mathcal {D},\mathbb {C})^G$ is supported in even degrees and is isomorphic to the complex
$\Omega ^\bullet (\mathcal {D}\times \mathcal {D},\mathbb {C})^G$ is supported in even degrees and is isomorphic to the complex ![]() $H^{\bullet }_{dR}(\widehat {\mathcal {D}}\times \widehat {\mathcal {D}},\mathbb {C})$.
$H^{\bullet }_{dR}(\widehat {\mathcal {D}}\times \widehat {\mathcal {D}},\mathbb {C})$.
Recall the following classical result. Let ![]() $X$ be a closed orientable smooth manifold of dimension
$X$ be a closed orientable smooth manifold of dimension ![]() $n$. For all
$n$. For all ![]() $0\leq k \leq n$, let us fix a basis
$0\leq k \leq n$, let us fix a basis ![]() $([\alpha ^{k,i}])_{i\in J_k}$ of
$([\alpha ^{k,i}])_{i\in J_k}$ of ![]() $H^k(X,\mathbb {C})$ and denote by
$H^k(X,\mathbb {C})$ and denote by ![]() $(\alpha _{k,i}^\vee )_{i\in J_k}$ the dual basis of
$(\alpha _{k,i}^\vee )_{i\in J_k}$ the dual basis of ![]() $H^{n-k}(X,\mathbb {C})$ with respect to Poincaré pairing. Let
$H^{n-k}(X,\mathbb {C})$ with respect to Poincaré pairing. Let ![]() $\pi _1,\pi _2:X\times X\rightarrow X$ denote the projections onto the first and the second factor, respectively. Then by [Reference Bott and TuBT82, Lemma 1.22], the cycle class of the diagonal
$\pi _1,\pi _2:X\times X\rightarrow X$ denote the projections onto the first and the second factor, respectively. Then by [Reference Bott and TuBT82, Lemma 1.22], the cycle class of the diagonal ![]() $\Delta (X)\hookrightarrow X\times X$ is Poincaré-dual to the de Rham cohomology class
$\Delta (X)\hookrightarrow X\times X$ is Poincaré-dual to the de Rham cohomology class
 \begin{equation} \gamma_X=\sum_{k=0}^{n} (-1)^{n(n-k)} \sum_{i\in J_k}\pi_1^*[\alpha_{k,i}^\vee]\wedge\pi_2^*[\alpha_{k,i}] \in H_{dR}^n(X\times X,\mathbb{C}). \end{equation}
\begin{equation} \gamma_X=\sum_{k=0}^{n} (-1)^{n(n-k)} \sum_{i\in J_k}\pi_1^*[\alpha_{k,i}^\vee]\wedge\pi_2^*[\alpha_{k,i}] \in H_{dR}^n(X\times X,\mathbb{C}). \end{equation} We can now state the main theorem of this section. Let ![]() $(\gamma _{k,i})_{i\in J_k}$ be a basis of
$(\gamma _{k,i})_{i\in J_k}$ be a basis of ![]() $\Omega ^{2k}(\mathcal {D}, \mathbb {C})^{G_1}$ and let
$\Omega ^{2k}(\mathcal {D}, \mathbb {C})^{G_1}$ and let ![]() $(\gamma _{k,i}^\vee )_{i\in J_k}$ denote the dual basis of
$(\gamma _{k,i}^\vee )_{i\in J_k}$ denote the dual basis of ![]() $\Omega ^{2d-2k}(\mathcal {D},\mathbb {C})^{G_1}$, i.e. such that
$\Omega ^{2d-2k}(\mathcal {D},\mathbb {C})^{G_1}$, i.e. such that
where ![]() $\omega _{\mathcal {D}}$ denotes the invariant volume form of
$\omega _{\mathcal {D}}$ denotes the invariant volume form of ![]() $\mathcal {D}\simeq G/K$ as in § 2.3.
$\mathcal {D}\simeq G/K$ as in § 2.3.
Theorem 5.22 Set ![]() $G= G_1\times G_1$,
$G= G_1\times G_1$, ![]() $K = K_1\times K_1$ where
$K = K_1\times K_1$ where ![]() $K_1$ is a maximal compact subgroup of
$K_1$ is a maximal compact subgroup of ![]() $G$ and take
$G$ and take ![]() $H$ the diagonal embedding of
$H$ the diagonal embedding of ![]() $G_1$ into
$G_1$ into ![]() $G$. Let
$G$. Let ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ denote the projections of
$\pi _2$ denote the projections of ![]() $G/K= \mathcal {D} \times \mathcal {D}$ on the first and second factor. Then
$G/K= \mathcal {D} \times \mathcal {D}$ on the first and second factor. Then
 \[ \frac{1}{\operatorname{Vol}(G_U/H_U)}\pi_*p^*\omega_{G/H}=\sum_{\underset{i\in J_k}{0\leq k\leq d}}\pi_1^*(\gamma_{k,i}^\vee)\wedge \pi_2^*(\gamma_{k,i}). \]
\[ \frac{1}{\operatorname{Vol}(G_U/H_U)}\pi_*p^*\omega_{G/H}=\sum_{\underset{i\in J_k}{0\leq k\leq d}}\pi_1^*(\gamma_{k,i}^\vee)\wedge \pi_2^*(\gamma_{k,i}). \]
In particular, its pull-back by the diagonal embedding ![]() $\Delta$ of
$\Delta$ of ![]() $\mathcal {D}$ is given by
$\mathcal {D}$ is given by
 \[ \frac{1}{\operatorname{Vol}(G_U/H_U)}\Delta^{*}\pi_*p^*\omega_{G/H}=\frac{\chi(\widehat{ \mathcal{D}})}{\operatorname{Vol}(\widehat{ \mathcal{D}})}\,\omega_{\mathcal{D}}. \]
\[ \frac{1}{\operatorname{Vol}(G_U/H_U)}\Delta^{*}\pi_*p^*\omega_{G/H}=\frac{\chi(\widehat{ \mathcal{D}})}{\operatorname{Vol}(\widehat{ \mathcal{D}})}\,\omega_{\mathcal{D}}. \]
where ![]() $\chi (\widehat {\mathcal {D}})>0$ is the Euler characteristic of
$\chi (\widehat {\mathcal {D}})>0$ is the Euler characteristic of ![]() $\widehat {\mathcal {D}}$.
$\widehat {\mathcal {D}}$.
Proof. By Corollary 4.8 and Lemma 4.9, it is enough to determine the cohomology class of the corresponding pull–push form on the compact dual ![]() $\widehat { \mathcal {D}} \times \widehat {\mathcal {D}}$. By Lemma 4.9, this cohomology class is Poincaré dual to the diagonal embedding of
$\widehat { \mathcal {D}} \times \widehat {\mathcal {D}}$. By Lemma 4.9, this cohomology class is Poincaré dual to the diagonal embedding of ![]() $\widehat {\mathcal {D}}$. The conclusion now follows from (5.4.1).
$\widehat {\mathcal {D}}$. The conclusion now follows from (5.4.1).
5.4.3 Hodge locus in Shimura varieties
In this section, we prove Theorem 1.17 and Corollary 1.18.
Let ![]() $G$ be a semi-simple Lie group of Hermitian type, let
$G$ be a semi-simple Lie group of Hermitian type, let ![]() $\mathcal {D}$ be the associated Hermitian symmetric space, let
$\mathcal {D}$ be the associated Hermitian symmetric space, let ![]() $\Gamma \subset G$ be an arithmetic subgroup, and let
$\Gamma \subset G$ be an arithmetic subgroup, and let ![]() $S=\Gamma \backslash D$. Let
$S=\Gamma \backslash D$. Let ![]() $(H,\mathcal {D}_H)$ be a Shimura subdatum such that
$(H,\mathcal {D}_H)$ be a Shimura subdatum such that ![]() $\pi _*p^*\omega _{G/H}$ is a positive form of type
$\pi _*p^*\omega _{G/H}$ is a positive form of type ![]() $(k,k)$. In particular, its restriction to any subvariety of
$(k,k)$. In particular, its restriction to any subvariety of ![]() $S$ of dimension at least
$S$ of dimension at least ![]() $k$ is non-zero. Hence, by the equivalences from Proposition 5.9, the Hodge locus in
$k$ is non-zero. Hence, by the equivalences from Proposition 5.9, the Hodge locus in ![]() $X$ is analytically dense and equidistributed with respect to
$X$ is analytically dense and equidistributed with respect to ![]() $\pi _*p^*\omega _{G/H}$.
$\pi _*p^*\omega _{G/H}$.
For the second part of the theorem, the pull–push form associated with ![]() $G/H$ is a
$G/H$ is a ![]() $(1,1)$-form and since
$(1,1)$-form and since ![]() $G$ is absolutely irreducible, there is, up to a scalar, a unique
$G$ is absolutely irreducible, there is, up to a scalar, a unique ![]() $(1,1)$-from on
$(1,1)$-from on ![]() $\mathcal {D}$ which is given as the Chern form of the canonical bundle on
$\mathcal {D}$ which is given as the Chern form of the canonical bundle on ![]() $\mathcal {D}$. The latter is known to be Kähler. Hence,
$\mathcal {D}$. The latter is known to be Kähler. Hence, ![]() $\pi _*p^*\omega _{G/H}$ is Kähler and we conclude as before.
$\pi _*p^*\omega _{G/H}$ is Kähler and we conclude as before.
We now prove Corollary 1.18. Let ![]() $n\geq 1$ and let
$n\geq 1$ and let ![]() $G=\mathrm {SU}(n,1)$. For
$G=\mathrm {SU}(n,1)$. For ![]() $1\leq r\leq n$, let
$1\leq r\leq n$, let ![]() $H=\mathrm {SU}(n-r,1)$. Let
$H=\mathrm {SU}(n-r,1)$. Let ![]() $K=S(U(1)\times U(n))$ be the maximal compact subgroup of
$K=S(U(1)\times U(n))$ be the maximal compact subgroup of ![]() $G$ and let
$G$ and let ![]() $\mathcal {D}=\mathbb {B}^{n}\simeq G/K$ be the unit ball which is isomorphic to the symmetric space of
$\mathcal {D}=\mathbb {B}^{n}\simeq G/K$ be the unit ball which is isomorphic to the symmetric space of ![]() $G$. The natural
$G$. The natural ![]() $1$-dimensional representation of
$1$-dimensional representation of ![]() $U(1)$ on the determinant of the cotangent bundle of
$U(1)$ on the determinant of the cotangent bundle of ![]() $\mathcal {D}$ determines a Hermitian line bundle on
$\mathcal {D}$ determines a Hermitian line bundle on ![]() $\mathbb {B}^{n}$ with first Chern form
$\mathbb {B}^{n}$ with first Chern form ![]() $\omega$. Using a similar method as in Theorem 5.21, one can easily prove the following.
$\omega$. Using a similar method as in Theorem 5.21, one can easily prove the following.
Proposition 5.23 We have ![]() $\pi _*p^*\omega _{G/H}=\operatorname {Vol}(G_U/H_U)\omega ^r$.
$\pi _*p^*\omega _{G/H}=\operatorname {Vol}(G_U/H_U)\omega ^r$.
Let ![]() $\Gamma$ be a neat arithmetic subgroup of
$\Gamma$ be a neat arithmetic subgroup of ![]() $G$. The quotient
$G$. The quotient ![]() $S=\Gamma \backslash \mathbb {B}^n$ is a unitary Shimura variety and the form
$S=\Gamma \backslash \mathbb {B}^n$ is a unitary Shimura variety and the form ![]() $\omega$ is Kähler on
$\omega$ is Kähler on ![]() $S$. If
$S$. If ![]() $r=1$, then we are in the situation of Theorem 1.17. Hence, the Hodge locus is dense and equidistributed in any subvariety of
$r=1$, then we are in the situation of Theorem 1.17. Hence, the Hodge locus is dense and equidistributed in any subvariety of ![]() $S$ of positive dimension.
$S$ of positive dimension.
5.4.4 Hodge locus in  $\mathcal {A}_g$
$\mathcal {A}_g$
In this section, we prove Theorem 1.14.
Let ![]() $(V,\Psi )$ be a rational vector space of dimension
$(V,\Psi )$ be a rational vector space of dimension ![]() $2g$ endowed with a non-degenerate symplectic form
$2g$ endowed with a non-degenerate symplectic form ![]() $\Psi$. Let
$\Psi$. Let ![]() $G=\mathrm {Sp}_{2g}(\mathbb {R})$ and let
$G=\mathrm {Sp}_{2g}(\mathbb {R})$ and let ![]() $\mathbb {H}_g$ be the Siegel upper-half space which is the Hermitian space associated with
$\mathbb {H}_g$ be the Siegel upper-half space which is the Hermitian space associated with ![]() $G$.
$G$.
For ![]() $1\leq k\leq {g}/{2}$, let
$1\leq k\leq {g}/{2}$, let ![]() $V_k\subseteq V$ be a non-degenerate rational subspace of rank
$V_k\subseteq V$ be a non-degenerate rational subspace of rank ![]() $2k$ and let
$2k$ and let ![]() $H\subseteq G$ be the stabilizer of
$H\subseteq G$ be the stabilizer of ![]() $V_k$ in
$V_k$ in ![]() $G$. Then
$G$. Then ![]() $H\simeq \mathrm {Sp}_{2k}(\mathbb {R})\times \mathrm {Sp}_{2g-2k}(\mathbb {R})$ and its symmetric space is equal to
$H\simeq \mathrm {Sp}_{2k}(\mathbb {R})\times \mathrm {Sp}_{2g-2k}(\mathbb {R})$ and its symmetric space is equal to ![]() $\mathbb {H}_k\times \mathbb {H}_{g-k}$.
$\mathbb {H}_k\times \mathbb {H}_{g-k}$.
To compute the pull–push form ![]() $\pi _*p^*\omega _{G/H}$, we follow the general method explained in §§ 4 and 5. The compact dual
$\pi _*p^*\omega _{G/H}$, we follow the general method explained in §§ 4 and 5. The compact dual ![]() $Y_g$ of
$Y_g$ of ![]() $\mathbb {H}_g$ is equal to the space of Lagrangian subspaces of
$\mathbb {H}_g$ is equal to the space of Lagrangian subspaces of ![]() $V_\mathbb {C}$ and the compact dual of
$V_\mathbb {C}$ and the compact dual of ![]() $\mathbb {H}_k\times \mathbb {H}_{g-k}$ is the subspace
$\mathbb {H}_k\times \mathbb {H}_{g-k}$ is the subspace ![]() $Y_k\times Y_{g-k}$ where
$Y_k\times Y_{g-k}$ where ![]() $Y_k$ and
$Y_k$ and ![]() $Y_{g-k}$ are the space of Lagrangian subspaces of
$Y_{g-k}$ are the space of Lagrangian subspaces of ![]() $V_{k,\mathbb {C}}$ and
$V_{k,\mathbb {C}}$ and ![]() $V_{k,\mathbb {C}}^{\perp }$ respectively. The inclusion
$V_{k,\mathbb {C}}^{\perp }$ respectively. The inclusion ![]() $Y_k\times Y_{g-k}\hookrightarrow Y_g$ is then given by taking direct sums of Lagrangians in a compatible way with the decomposition
$Y_k\times Y_{g-k}\hookrightarrow Y_g$ is then given by taking direct sums of Lagrangians in a compatible way with the decomposition ![]() $V_\mathbb {C}=V_{k,\mathbb {C}}\oplus V_{k,\mathbb {C}}^\bot$.
$V_\mathbb {C}=V_{k,\mathbb {C}}\oplus V_{k,\mathbb {C}}^\bot$.
Let ![]() $\mathcal {V}\rightarrow Y_g$ be the trivial vector bundle of rank
$\mathcal {V}\rightarrow Y_g$ be the trivial vector bundle of rank ![]() $2g$ determined by
$2g$ determined by ![]() $V$ and let
$V$ and let ![]() $\widehat {\mathcal {F}}^{1}\rightarrow Y_g$ be the Hodge vector bundle whose restriction to
$\widehat {\mathcal {F}}^{1}\rightarrow Y_g$ be the Hodge vector bundle whose restriction to ![]() $\mathbb {H}_g$ will be denoted simply
$\mathbb {H}_g$ will be denoted simply ![]() $\mathcal {F}^{1}$. Let
$\mathcal {F}^{1}$. Let ![]() $\mathcal {V}_k$ be the trivial vector bundle determined by
$\mathcal {V}_k$ be the trivial vector bundle determined by ![]() $V_k$. Then we have a natural map of vector bundles:
$V_k$. Then we have a natural map of vector bundles:
The locus where this map has rank at most ![]() $k$ corresponds to the locus where the rank of the kernel is at least
$k$ corresponds to the locus where the rank of the kernel is at least ![]() $k$. Since the kernel is Lagrangian in
$k$. Since the kernel is Lagrangian in ![]() $V_k$, it is also the locus where the rank is exactly
$V_k$, it is also the locus where the rank is exactly ![]() $k$ and hence it is equal to
$k$ and hence it is equal to ![]() $Y_k\times Y_{g-k}$. By the Giambelli–Porteous–Thom formula [Reference Kempf and LaksovKL74], the locus
$Y_k\times Y_{g-k}$. By the Giambelli–Porteous–Thom formula [Reference Kempf and LaksovKL74], the locus ![]() $Y_k\times Y_{g-k}$ is Poincaré dual to the class
$Y_k\times Y_{g-k}$ is Poincaré dual to the class
By Corollary 4.8 and Proposition 5.16, we have
 \begin{align*} \pi_*p^*\omega_{G/H}&=i^{2k(g-k)}\pi_*p^*\omega_{G_U/H_U}\\ &=(-1)^{k(g-k)}\operatorname{Vol}(G_U/H_U)\det\bigl(((-1)^{g-k+i-j}c_{g-k+i-j}({\mathcal{F}}^{1}))_{1\leq i,j\leq k}\bigr)\\ &=\operatorname{Vol}(G_U/H_U)\det\bigl(((-1)^{i-j}c_{g-k+i-j}(\mathcal{F}^{1}))_{1\leq i,j\leq k}\bigr)\\ &=\operatorname{Vol}(G_U/H_U)s_k. \end{align*}
\begin{align*} \pi_*p^*\omega_{G/H}&=i^{2k(g-k)}\pi_*p^*\omega_{G_U/H_U}\\ &=(-1)^{k(g-k)}\operatorname{Vol}(G_U/H_U)\det\bigl(((-1)^{g-k+i-j}c_{g-k+i-j}({\mathcal{F}}^{1}))_{1\leq i,j\leq k}\bigr)\\ &=\operatorname{Vol}(G_U/H_U)\det\bigl(((-1)^{i-j}c_{g-k+i-j}(\mathcal{F}^{1}))_{1\leq i,j\leq k}\bigr)\\ &=\operatorname{Vol}(G_U/H_U)s_k. \end{align*}
Now combining Proposition 5.9, and Theorem 1.1, the first part of Theorem 1.14 follows easily. For the second part, we use the main theorem of [Reference Keel and SadunKS03] which stipulates that ![]() $s_1=c_{g-1}$ is non-zero restricted to any compact subvariety of dimension
$s_1=c_{g-1}$ is non-zero restricted to any compact subvariety of dimension ![]() $>({(g-1)(g-2)})/{2}$.
$>({(g-1)(g-2)})/{2}$.
6. Applications
We discuss in this section various applications of Theorem 1.1. They concern mainly equidistribution of Hodge loci in variations of Hodge structures, in particular in the context of weight-two Hodge structures and Hodge structures parametrized by Shimura varieties. For an introduction to these topics, we refer the reader to [Reference VoisinVoi02, III,VI] and [Reference Green, Griffiths and KerrGGK12].
6.1 Refined Noether–Lefschetz loci in  $\mathbb {Z}$-PVHS of weight two.
$\mathbb {Z}$-PVHS of weight two.
Let ![]() $\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a polarized variation of Hodge structure of weight two over a smooth complex quasi-projective variety
$\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a polarized variation of Hodge structure of weight two over a smooth complex quasi-projective variety ![]() $X$. Assume as before that the local system
$X$. Assume as before that the local system ![]() $(\mathbb {V}_\mathbb {Z},B)$ has fibers isomorphic to a quadratic lattice
$(\mathbb {V}_\mathbb {Z},B)$ has fibers isomorphic to a quadratic lattice ![]() $(V_\mathbb {Z},B)$ equipped with a bilinear form
$(V_\mathbb {Z},B)$ equipped with a bilinear form
with associated quadratic form ![]() ${B(y,y)}/{2}\in \mathbb {Z}$ for
${B(y,y)}/{2}\in \mathbb {Z}$ for ![]() $y\in V_\mathbb {Z}$. Let
$y\in V_\mathbb {Z}$. Let ![]() $(q,p,q)$ be the Hodge numbers and
$(q,p,q)$ be the Hodge numbers and ![]() $d=p+2q$ the rank of
$d=p+2q$ the rank of ![]() $\mathbb {V}_\mathbb {Z}$.
$\mathbb {V}_\mathbb {Z}$.
For ![]() $x\in X$, let
$x\in X$, let ![]() $\rho (x)$ be the rank of the Picard group
$\rho (x)$ be the rank of the Picard group ![]() $\mathrm {Pic}(x)=\mathcal {F}^1\mathcal {V}_x\cap \mathbb {V}_{\mathbb {Z},x}$. Assume that the variation is simple, i.e.
$\mathrm {Pic}(x)=\mathcal {F}^1\mathcal {V}_x\cap \mathbb {V}_{\mathbb {Z},x}$. Assume that the variation is simple, i.e. ![]() $\rho (x)=0$ at a very general point. For
$\rho (x)=0$ at a very general point. For ![]() $r\geq 1$, we introduce the refined Noether–Lefschetz locus Footnote 6
$r\geq 1$, we introduce the refined Noether–Lefschetz locus Footnote 6
It corresponds to a sub-Hodge locus for ![]() $\mathbb {V}_\mathbb {Z}^{r}$. It can be written as the union over algebraic subvarieties in the two following ways.
$\mathbb {V}_\mathbb {Z}^{r}$. It can be written as the union over algebraic subvarieties in the two following ways.
(i) It is the union, over all integers
 $N\geq 1$, of the sets
$N\geq 1$, of the sets
 \[ \{x\in X\mid \exists P\subseteq \mathrm{Pic}(x) \text{ of rank $r$}, \operatorname{disc}(P)\leq N \}. \]
\[ \{x\in X\mid \exists P\subseteq \mathrm{Pic}(x) \text{ of rank $r$}, \operatorname{disc}(P)\leq N \}. \]
(ii) It is the union, over all positive-definite symmetric matrices
 $M\in M_r(\mathbb {Z})$, of the sets
$M\in M_r(\mathbb {Z})$, of the sets
 \[ \big\{x\in X\mid \exists (\lambda_1,\ldots,\lambda_r)\in \mathrm{Pic}(x), \big(B(\lambda_i\cdot\lambda_j)\big)_{1\leq i,j\leq r}=M \big\}. \]
\[ \big\{x\in X\mid \exists (\lambda_1,\ldots,\lambda_r)\in \mathrm{Pic}(x), \big(B(\lambda_i\cdot\lambda_j)\big)_{1\leq i,j\leq r}=M \big\}. \]
We prove in the next two subsections that both formulations give equidistribution results and, hence, we prove Theorems 1.6 and 1.7 by using different techniques in each case.
6.1.1 Equidistribution on average
Let ![]() $x$ be a point in
$x$ be a point in ![]() $X$ and denote by
$X$ and denote by ![]() $(V_\mathbb {Z},B,F^\bullet )$ the fiber at
$(V_\mathbb {Z},B,F^\bullet )$ the fiber at ![]() $x$ of
$x$ of ![]() $\mathbb {V}$. As in the previous section, we set
$\mathbb {V}$. As in the previous section, we set ![]() $G= \mathrm O(V_\mathbb {R}, B)$,
$G= \mathrm O(V_\mathbb {R}, B)$, ![]() $\Gamma = \mathrm O(V_\mathbb {Z},B)$, and let
$\Gamma = \mathrm O(V_\mathbb {Z},B)$, and let ![]() $K\subset G$ be the stabilizer of
$K\subset G$ be the stabilizer of ![]() $F^\bullet$. Finally, let
$F^\bullet$. Finally, let ![]() $H$ denote the stabilizer of a positive-definite subspace of
$H$ denote the stabilizer of a positive-definite subspace of ![]() $V_\mathbb {R}$ of dimension
$V_\mathbb {R}$ of dimension ![]() $r$, so that
$r$, so that ![]() $G/H$ identifies with the space
$G/H$ identifies with the space ![]() $\mathcal {P}$ of positive-definite real subspaces of dimension
$\mathcal {P}$ of positive-definite real subspaces of dimension ![]() $r$.
$r$.
Define the discriminant of a rational subspace ![]() $W\in \mathcal {P}$ as the determinant of the intersection matrix
$W\in \mathcal {P}$ as the determinant of the intersection matrix
where ![]() $(v_i)$ is a basis of
$(v_i)$ is a basis of ![]() $W\cap V_{\mathbb {Z}}$. We denote by
$W\cap V_{\mathbb {Z}}$. We denote by ![]() $\mathcal {P}_n$ the discrete subset of
$\mathcal {P}_n$ the discrete subset of ![]() $\mathcal {P}$ consisting of rational subspaces of discriminant at most
$\mathcal {P}$ consisting of rational subspaces of discriminant at most ![]() $n$. The set
$n$. The set ![]() $\mathcal {P}_n$ is a finite union of
$\mathcal {P}_n$ is a finite union of ![]() $\Gamma$-orbits of
$\Gamma$-orbits of ![]() $G/H$, corresponding to a finite union
$G/H$, corresponding to a finite union ![]() $\mathcal {O}_n$ of closed
$\mathcal {O}_n$ of closed ![]() $H$-orbits in
$H$-orbits in ![]() $\Gamma \backslash G$. We prove here that
$\Gamma \backslash G$. We prove here that ![]() $\mathcal {P}_n$ is equidistributed in
$\mathcal {P}_n$ is equidistributed in ![]() $G/H$.
$G/H$.
Theorem 6.1 The sequence ![]() $(\mathcal {P}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {P}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $G/H$.
$G/H$.
The proof we give here is a refinement of the fact that integral vectors of length at most ![]() $n$ equidistribute. Some trick is needed in order to get rid of multiplicities, but the proof is ‘elementary’ in the sense that it does not rely on any involved argument such as the circle method, automorphic functions or Ratner theory. Of course, by counting all rational subspaces of length less than
$n$ equidistribute. Some trick is needed in order to get rid of multiplicities, but the proof is ‘elementary’ in the sense that it does not rely on any involved argument such as the circle method, automorphic functions or Ratner theory. Of course, by counting all rational subspaces of length less than ![]() $n$, we avoid all the difficult arithmetic questions that arise when looking at rational subspaces of a fixed discriminant.
$n$, we avoid all the difficult arithmetic questions that arise when looking at rational subspaces of a fixed discriminant.
Let ![]() $\Omega$ denote the open cone of
$\Omega$ denote the open cone of ![]() $V_\mathbb {R}^r$ consisting of tuples of vectors spanning a positive-definite subspace of dimension
$V_\mathbb {R}^r$ consisting of tuples of vectors spanning a positive-definite subspace of dimension ![]() $r$. The function
$r$. The function
 \begin{align*} h:\Omega &\to \mathbb{R}_{>0} \\ \underline v=(v_1,\ldots, v_r)&\mapsto \det\big(B(v_i,v_j)\big)_{1\leq i,j\leq r} \end{align*}
\begin{align*} h:\Omega &\to \mathbb{R}_{>0} \\ \underline v=(v_1,\ldots, v_r)&\mapsto \det\big(B(v_i,v_j)\big)_{1\leq i,j\leq r} \end{align*}
is homogeneous of degree ![]() $2r$. We denote by
$2r$. We denote by ![]() $\Omega _1$ the hypersurface
$\Omega _1$ the hypersurface ![]() $\{\underline v\in \Omega \mid h(\underline v) = 1\}$ and by
$\{\underline v\in \Omega \mid h(\underline v) = 1\}$ and by ![]() $\Omega _{\leq 1}$ the subset
$\Omega _{\leq 1}$ the subset ![]() $\{\underline v \mid h(\underline v) \leq 1\}$. We denote by
$\{\underline v \mid h(\underline v) \leq 1\}$. We denote by
the projection map
We endow ![]() $V_\mathbb {R}^r$ with the Lebesgue measure for which
$V_\mathbb {R}^r$ with the Lebesgue measure for which ![]() $V_\mathbb {Z}^r$ has covolume one and denote by
$V_\mathbb {Z}^r$ has covolume one and denote by ![]() $\omega$ the push-forward by
$\omega$ the push-forward by ![]() $pr$ of the Lebesgue measure restricted to
$pr$ of the Lebesgue measure restricted to ![]() $\Omega _{\leq 1}$, i.e. the volume form such that
$\Omega _{\leq 1}$, i.e. the volume form such that
 \[ \int_U \omega = \mathrm{Leb}\biggl(\bigcup_{0< t \leq 1} tU\biggr).\]
\[ \int_U \omega = \mathrm{Leb}\biggl(\bigcup_{0< t \leq 1} tU\biggr).\]
Define
and let ![]() $\mu _n$ be the counting measure of
$\mu _n$ be the counting measure of ![]() $pr(\mathcal {Q}_n)$, i.e.
$pr(\mathcal {Q}_n)$, i.e.
We first prove the following elementary counting result.
Proposition 6.2 The sequence of measures ![]() $n^{-{d}/{2}}\mu _n$ converges weakly to the smooth measure
$n^{-{d}/{2}}\mu _n$ converges weakly to the smooth measure ![]() $\omega$.
$\omega$.
Proof. Let ![]() $f:\Omega _1 \to \mathbb {R}$ be a continuous function with compact support which we extend on
$f:\Omega _1 \to \mathbb {R}$ be a continuous function with compact support which we extend on ![]() $\Omega$ by setting
$\Omega$ by setting ![]() $f(t\underline v)=f(\underline v)$ for all
$f(t\underline v)=f(\underline v)$ for all ![]() $t\in \mathbb {R}_{>0}$ and all
$t\in \mathbb {R}_{>0}$ and all ![]() $\underline v\in \Omega _1$. We have
$\underline v\in \Omega _1$. We have
 \begin{align*} n^{-{d}/{2}}\mu_n(f)& =n^{-{d}/{2}} \sum_{\underline v\in V_\mathbb{Z}^r \cap \Omega\mid h(\underline v)\leq n} f(\underline v)\\ &=n^{-{d}/{2}} \sum_{\underline v\in n^{-{1}/{2r}}V_\mathbb{Z}^r \cap \Omega\mid h(\underline v)\leq 1} f(\underline v) \quad \text{by homogeneity of }f\\ & \underset{n\to +\infty}{\longrightarrow} \int_{\Omega_{\leq 1}} f = \omega(f)\quad \text{by Riemann summation.}\quad \end{align*}
\begin{align*} n^{-{d}/{2}}\mu_n(f)& =n^{-{d}/{2}} \sum_{\underline v\in V_\mathbb{Z}^r \cap \Omega\mid h(\underline v)\leq n} f(\underline v)\\ &=n^{-{d}/{2}} \sum_{\underline v\in n^{-{1}/{2r}}V_\mathbb{Z}^r \cap \Omega\mid h(\underline v)\leq 1} f(\underline v) \quad \text{by homogeneity of }f\\ & \underset{n\to +\infty}{\longrightarrow} \int_{\Omega_{\leq 1}} f = \omega(f)\quad \text{by Riemann summation.}\quad \end{align*}
The group ![]() $G \times \operatorname {SL}(r,\mathbb {R})$ acts transitively on
$G \times \operatorname {SL}(r,\mathbb {R})$ acts transitively on ![]() $\Omega _1$ by
$\Omega _1$ by
and preserves the measure ![]() $\omega$. The restriction of this action to
$\omega$. The restriction of this action to ![]() $\operatorname {SL}(r,\mathbb {R})$ is proper and the quotient
$\operatorname {SL}(r,\mathbb {R})$ is proper and the quotient ![]() $\operatorname {SL}(r,\mathbb {R}) \backslash \Omega _1$ is the space
$\operatorname {SL}(r,\mathbb {R}) \backslash \Omega _1$ is the space ![]() $\mathcal {P}$ or positive-definite
$\mathcal {P}$ or positive-definite ![]() $r$-subspaces of
$r$-subspaces of ![]() $V_\mathbb {R}$.
$V_\mathbb {R}$.
Now, the subgroup ![]() $\operatorname {SL}(r,\mathbb {Z})$ preserves the set
$\operatorname {SL}(r,\mathbb {Z})$ preserves the set ![]() $\mathcal {Q}_n$ and acts properly discontinuously on
$\mathcal {Q}_n$ and acts properly discontinuously on ![]() $\Omega _1$ so that the quotient set
$\Omega _1$ so that the quotient set ![]() $\bar {\mathcal {Q}}_n = \operatorname {SL}(r,\mathbb {Z}) \backslash \mathcal {Q}_n$ still equidistributes in
$\bar {\mathcal {Q}}_n = \operatorname {SL}(r,\mathbb {Z}) \backslash \mathcal {Q}_n$ still equidistributes in ![]() $\operatorname {SL}(r,\mathbb {Z})\backslash \Omega _1$. Let us consider the projection
$\operatorname {SL}(r,\mathbb {Z})\backslash \Omega _1$. Let us consider the projection
We still use ![]() $\omega$ to denote the volume form induced on
$\omega$ to denote the volume form induced on ![]() $\operatorname {SL}(r,\mathbb {Z})\backslash \Omega _1$. The push-forward measure
$\operatorname {SL}(r,\mathbb {Z})\backslash \Omega _1$. The push-forward measure ![]() $\pi _*\omega$ is
$\pi _*\omega$ is ![]() $G$-invariant (because
$G$-invariant (because ![]() $\omega$ is
$\omega$ is ![]() $G$-invariant and
$G$-invariant and ![]() $\pi$ is
$\pi$ is ![]() $G$-equivariant), non-zero, and locally finite because
$G$-equivariant), non-zero, and locally finite because ![]() $\operatorname {SL}(n,\mathbb {Z})\backslash \operatorname {SL}(n,\mathbb {R})$ has finite volume. We hence deduce the following result from Proposition 6.2.
$\operatorname {SL}(n,\mathbb {Z})\backslash \operatorname {SL}(n,\mathbb {R})$ has finite volume. We hence deduce the following result from Proposition 6.2.
Corollary 6.3 Define the measure
Then
for some ![]() $\lambda \neq 0$.
$\lambda \neq 0$.
Remark 6.4 The multiplicative constant ![]() $\lambda$ could be computed in terms of the volume of
$\lambda$ could be computed in terms of the volume of ![]() $\operatorname {SL}(n,\mathbb {R})/\operatorname {SL}(n,\mathbb {Z})$.
$\operatorname {SL}(n,\mathbb {R})/\operatorname {SL}(n,\mathbb {Z})$.
The measure ![]() $\nu _n$, however, is not the counting measure of
$\nu _n$, however, is not the counting measure of ![]() $\mathcal {P}_n$. To be more precise, note that
$\mathcal {P}_n$. To be more precise, note that ![]() $\bar {\mathcal {Q}}_n$ is the set of positive-definite sublattices of
$\bar {\mathcal {Q}}_n$ is the set of positive-definite sublattices of ![]() $V_\mathbb {Z}$ of discriminant at most
$V_\mathbb {Z}$ of discriminant at most ![]() $n$ and
$n$ and ![]() $\pi$ maps
$\pi$ maps ![]() $\Lambda \in \bar {\mathcal {Q}}_n$ to
$\Lambda \in \bar {\mathcal {Q}}_n$ to ![]() $\Lambda \otimes \mathbb {R}$. Therefore, we have
$\Lambda \otimes \mathbb {R}$. Therefore, we have
where
In other words, ![]() $\nu _n$ counts a rational subspace
$\nu _n$ counts a rational subspace ![]() $W$ with a weight equal to the number of sublattices of
$W$ with a weight equal to the number of sublattices of ![]() $W\cap V_\mathbb {Z}$ with discriminant
$W\cap V_\mathbb {Z}$ with discriminant ![]() $\leq n$.
$\leq n$.
Let ![]() $\nu _n'$ be the counting measure of
$\nu _n'$ be the counting measure of ![]() $\mathcal {P}_n$. To relate
$\mathcal {P}_n$. To relate ![]() $\nu _n$ and
$\nu _n$ and ![]() $\nu _n'$, let us introduce
$\nu _n'$, let us introduce
We have the following estimate on ![]() $b_k$:
$b_k$:
Proposition 6.5
Proof. We prove a sharper estimate. Consider the zeta function which converges for large ![]() $s$:
$s$:
 \[ \zeta_{\mathbb{Z}^r}(s)=\sum_{k\geq 1}\frac{b_k}{k^s}=\sum_{g}|\det(g)|^{-s}, \]
\[ \zeta_{\mathbb{Z}^r}(s)=\sum_{k\geq 1}\frac{b_k}{k^s}=\sum_{g}|\det(g)|^{-s}, \]
where ![]() $g$ runs through
$g$ runs through ![]() $\mathrm {GL}_{r}(\mathbb {Z})\backslash (\mathrm {M}_{r}(\mathbb {Z})\cap \mathrm {GL}_r(\mathbb {Q}))$. By [Reference Lubotzky and SegalLS03, Equation (15.10)], we have the equality
$\mathrm {GL}_{r}(\mathbb {Z})\backslash (\mathrm {M}_{r}(\mathbb {Z})\cap \mathrm {GL}_r(\mathbb {Q}))$. By [Reference Lubotzky and SegalLS03, Equation (15.10)], we have the equality
 \[ \zeta_{\mathbb{Z}^r}(s)=\prod_{i=0}^{r-1}\zeta(s-i). \]
\[ \zeta_{\mathbb{Z}^r}(s)=\prod_{i=0}^{r-1}\zeta(s-i). \]
Hence, by identifying the coefficients, we obtain
 \begin{align*} b_k&=\sum_{\underset{k_0\cdots k_{r-1}=k}{(k_0,\ldots,k_{r-1})} }k_0\cdots k_{r-1}^{r-1}\\ &\leq k^{r-1}|\{(k_0,\ldots,k_{r-1}), k_0\cdots k_{r-1}=k\}|\\ &\ll_\epsilon k^{r-1+\epsilon} \end{align*}
\begin{align*} b_k&=\sum_{\underset{k_0\cdots k_{r-1}=k}{(k_0,\ldots,k_{r-1})} }k_0\cdots k_{r-1}^{r-1}\\ &\leq k^{r-1}|\{(k_0,\ldots,k_{r-1}), k_0\cdots k_{r-1}=k\}|\\ &\ll_\epsilon k^{r-1+\epsilon} \end{align*}
for every ![]() $\epsilon >0$. Hence, the result.
$\epsilon >0$. Hence, the result.
We now have
 \begin{align*} \nu_n &= \sum_{P\in
\mathcal{P}_n} \Biggl(\sum_{k\leq \sqrt
\frac{n}{h(P)}} b_k\Biggr) \delta_P\\ &=
\sum_{k\leq \sqrt{n}} \sum_{h(P)\leq {n}/{k^2}} b_k \delta_P \end{align*}
\begin{align*} \nu_n &= \sum_{P\in
\mathcal{P}_n} \Biggl(\sum_{k\leq \sqrt
\frac{n}{h(P)}} b_k\Biggr) \delta_P\\ &=
\sum_{k\leq \sqrt{n}} \sum_{h(P)\leq {n}/{k^2}} b_k \delta_P \end{align*}
and we conclude that
Set
Proposition 6.6 The measure ![]() $\nu '_n$ converges weakly to
$\nu '_n$ converges weakly to
Proof. Remark first that, under the hypothesis ![]() $1\leq r \leq p = d-2q \leq d-2$, we have
$1\leq r \leq p = d-2q \leq d-2$, we have
hence
Let ![]() $f$ be a continuous function with compact support on
$f$ be a continuous function with compact support on ![]() $G/H$. Set
$G/H$. Set
 \[ s_n = n^{-{d}/{2}}\frac{\nu_n(f)}{\lambda\int_{G/H} f \omega_{G/H}} \]
\[ s_n = n^{-{d}/{2}}\frac{\nu_n(f)}{\lambda\int_{G/H} f \omega_{G/H}} \]
and
 \[ s'_n = n^{-{d}/{2}}\frac{\nu'_n(f)}{\lambda\int_{G/H} f \omega_{G/H}}. \]
\[ s'_n = n^{-{d}/{2}}\frac{\nu'_n(f)}{\lambda\int_{G/H} f \omega_{G/H}}. \]
By (6.1.1), we have
 \begin{equation} s_n = \sum_{k\geq 1} n^{-{d}/{2}}\biggl \lfloor\frac{n}{k^2}\biggr \rfloor^{{d}/{2}} b_k s'_{\lfloor{n}/{k^2} \rfloor}. \end{equation}
\begin{equation} s_n = \sum_{k\geq 1} n^{-{d}/{2}}\biggl \lfloor\frac{n}{k^2}\biggr \rfloor^{{d}/{2}} b_k s'_{\lfloor{n}/{k^2} \rfloor}. \end{equation}By Proposition 6.2, we have
In particular, ![]() $(s_n)$ is bounded by a constant
$(s_n)$ is bounded by a constant ![]() $c$. Since
$c$. Since ![]() $s'_n \leq s_n$ the sequence
$s'_n \leq s_n$ the sequence ![]() $s'_n$ is also bounded and, by convergence of the series
$s'_n$ is also bounded and, by convergence of the series
we can find for all ![]() $\epsilon >0$ some
$\epsilon >0$ some ![]() $k_0$ such that
$k_0$ such that
 \[ \sum_{k\geq k_0} n^{-{d}/{2}}\biggl \lfloor\frac{n}{k^2}\biggr \rfloor^{{d}/{2}} b_k s'_{\lfloor{n}/{k^2} \rfloor}\leq \epsilon \]
\[ \sum_{k\geq k_0} n^{-{d}/{2}}\biggl \lfloor\frac{n}{k^2}\biggr \rfloor^{{d}/{2}} b_k s'_{\lfloor{n}/{k^2} \rfloor}\leq \epsilon \]
for all ![]() $n$.
$n$.
Set ![]() $m= \liminf s'_n$ and
$m= \liminf s'_n$ and ![]() $M=\limsup s'_n$, and let
$M=\limsup s'_n$, and let ![]() $n_i$ be a subsequence such that
$n_i$ be a subsequence such that ![]() $s'_{n_i} \underset {n\to +\infty }{\longrightarrow } m$. For all
$s'_{n_i} \underset {n\to +\infty }{\longrightarrow } m$. For all ![]() $2\leq k \leq k_0$ we have
$2\leq k \leq k_0$ we have
 \[ \limsup_{i\to +\infty} n_i^{-{d}/{2}}\biggl\lfloor\frac{n_i}{k^2}\biggr \rfloor^{{d}/{2}} s'_{\lfloor{n_i}/{k^2}\rfloor} = \leq \frac{b_k}{k^{d}} M. \]
\[ \limsup_{i\to +\infty} n_i^{-{d}/{2}}\biggl\lfloor\frac{n_i}{k^2}\biggr \rfloor^{{d}/{2}} s'_{\lfloor{n_i}/{k^2}\rfloor} = \leq \frac{b_k}{k^{d}} M. \]
Hence, taking the limsup of (6.1.2) along ![]() $n_i$, we get
$n_i$, we get
 \[ 1 \leq m +\sum_{k=2}^{k_0} \frac{b_k}{k^{rd}}M + \epsilon = m + (\alpha-1)M + \epsilon. \]
\[ 1 \leq m +\sum_{k=2}^{k_0} \frac{b_k}{k^{rd}}M + \epsilon = m + (\alpha-1)M + \epsilon. \]
Similarly taking the liminf along a subsequence ![]() $n_i$ such that
$n_i$ such that ![]() $s'_{n_i} \underset {n\to +\infty }{\longrightarrow } \to M$, we obtain
$s'_{n_i} \underset {n\to +\infty }{\longrightarrow } \to M$, we obtain
Combining the two, we obtain
hence
because ![]() $\alpha < 2$.
$\alpha < 2$.
As this is true for all ![]() $\epsilon >0$, we conclude that
$\epsilon >0$, we conclude that ![]() $M=m$. Hence,
$M=m$. Hence, ![]() $s'_n$ converges to
$s'_n$ converges to ![]() $m=M$. Taking the limit in (6.1.2) gives
$m=M$. Taking the limit in (6.1.2) gives ![]() $1 = \alpha m$, and we conclude that
$1 = \alpha m$, and we conclude that
Going back to the definition of ![]() $s'_n$ we have proved that
$s'_n$ we have proved that
6.1.2 Equidistribution along intersection matrices
To prove the second version of the equidistribution theorem which yields Theorem 1.7, we can restrict to matrices ![]() $M$ which are primitively represented by
$M$ which are primitively represented by ![]() $(V_\mathbb {Z},B)$, i.e. for which there exists
$(V_\mathbb {Z},B)$, i.e. for which there exists ![]() $(\lambda _1,\ldots,\lambda _r)\in V_\mathbb {Z}^r$ generating a primitive sublattice of
$(\lambda _1,\ldots,\lambda _r)\in V_\mathbb {Z}^r$ generating a primitive sublattice of ![]() $\mathbb {V}_\mathbb {Z}$ and with intersection matrix
$\mathbb {V}_\mathbb {Z}$ and with intersection matrix ![]() $M$. For simplicity, if
$M$. For simplicity, if ![]() $\underline {\lambda }\in V_\mathbb {R}^r$, we denote by
$\underline {\lambda }\in V_\mathbb {R}^r$, we denote by ![]() $I(\underline {\lambda })$ the intersection matrix
$I(\underline {\lambda })$ the intersection matrix ![]() $(B(\lambda _i\cdot\lambda _j))_{1\leq i,j\leq r}$. Let
$(B(\lambda _i\cdot\lambda _j))_{1\leq i,j\leq r}$. Let
Then ![]() $V_{\mathbb {R},\mathrm {I}_r}^r$ is an affine homogeneous variety under the action of the group
$V_{\mathbb {R},\mathrm {I}_r}^r$ is an affine homogeneous variety under the action of the group ![]() $G=\mathrm {O}(V_\mathbb {R},B)\simeq \mathrm {O}(p,2q)$ and letting
$G=\mathrm {O}(V_\mathbb {R},B)\simeq \mathrm {O}(p,2q)$ and letting ![]() $H\simeq \mathrm {O}(p-r,2q)$ be the stabilizer of a point
$H\simeq \mathrm {O}(p-r,2q)$ be the stabilizer of a point ![]() $\underline {\lambda }_0\in V_{\mathbb {R},\mathrm {I}_r}^r$, then
$\underline {\lambda }_0\in V_{\mathbb {R},\mathrm {I}_r}^r$, then ![]() $V_{\mathbb {R},\mathrm {I}_r}^r\simeq G/H$. When
$V_{\mathbb {R},\mathrm {I}_r}^r\simeq G/H$. When ![]() $r< p$ and
$r< p$ and ![]() $q\geq 1$ the group
$q\geq 1$ the group ![]() $H$ is simple without compact factors, so that Ratner theory can be applied as explained in Theorem 2.16. Finally,
$H$ is simple without compact factors, so that Ratner theory can be applied as explained in Theorem 2.16. Finally, ![]() $H$ is not contained in any proper parabolic subgroup of
$H$ is not contained in any proper parabolic subgroup of ![]() $G$, so that sequences of closed
$G$, so that sequences of closed ![]() $H$-orbits of
$H$-orbits of ![]() $\Gamma \backslash G$ do not have loss of mass.
$\Gamma \backslash G$ do not have loss of mass.
There is a right action of an ![]() $r\times r$ matrix
$r\times r$ matrix ![]() $A=(a_{i,j})$ on a vector
$A=(a_{i,j})$ on a vector ![]() $\underline {u}=(u_1,\ldots,u_r)\in V_\mathbb {R}^r$ given by the matrix product
$\underline {u}=(u_1,\ldots,u_r)\in V_\mathbb {R}^r$ given by the matrix product
 \[ \underline{u}\cdot
A=\biggl(\sum_{j=1}^ra_{1,j}u_1,\ldots
,\sum_{j=1}^ra_{r,j}u_j\biggr). \]
\[ \underline{u}\cdot
A=\biggl(\sum_{j=1}^ra_{1,j}u_1,\ldots
,\sum_{j=1}^ra_{r,j}u_j\biggr). \]
Note that this action commutes with the diagonal action of ![]() $\mathrm {GL}(V_\mathbb {R})$ and that the components of
$\mathrm {GL}(V_\mathbb {R})$ and that the components of ![]() $\underline {u}\cdot A$ span a subspace of the vector space spanned by components of
$\underline {u}\cdot A$ span a subspace of the vector space spanned by components of ![]() $\underline {u}$ in
$\underline {u}$ in ![]() $V_\mathbb {R}$, and they are equal if
$V_\mathbb {R}$, and they are equal if ![]() $A$ is invertible. Their intersection matrices are related by
$A$ is invertible. Their intersection matrices are related by
Let ![]() $M$ be a positive-definite integral matrix of size
$M$ be a positive-definite integral matrix of size ![]() $r$ and let
$r$ and let
In order to study equidistribution of ![]() $W_M$, it is natural to first project it to
$W_M$, it is natural to first project it to ![]() $V_{\mathbb {R},\mathrm {I}_r}^r$. We have thus a
$V_{\mathbb {R},\mathrm {I}_r}^r$. We have thus a ![]() $G$-equivariant projection map
$G$-equivariant projection map
 \begin{align*} pr:W_M&\rightarrow V_{\mathbb{R},\mathrm{I}_r}^r\\ \underline{\lambda}&\mapsto \underline{\lambda}\cdot \sqrt{M}^{-1}, \end{align*}
\begin{align*} pr:W_M&\rightarrow V_{\mathbb{R},\mathrm{I}_r}^r\\ \underline{\lambda}&\mapsto \underline{\lambda}\cdot \sqrt{M}^{-1}, \end{align*}
where ![]() $\sqrt {M}$ is the unique positive-definite matrix such that
$\sqrt {M}$ is the unique positive-definite matrix such that ![]() $\sqrt {M}^2=M$.
$\sqrt {M}^2=M$.
By a theorem of Borel and Harish-Chandra [Reference Borel and Harish-ChandraBH62, Theorem 6.9], the projection ![]() $pr(W_M)$ is a finite union of discrete
$pr(W_M)$ is a finite union of discrete ![]() $\Gamma$-orbits of
$\Gamma$-orbits of ![]() $G/H$, which thus corresponds to a finite union of closed
$G/H$, which thus corresponds to a finite union of closed ![]() $H$-orbits
$H$-orbits ![]() $\mathcal {O}_M \subset \Gamma \backslash G$. The volume of
$\mathcal {O}_M \subset \Gamma \backslash G$. The volume of ![]() $\mathcal {O}_M$ is finite by Borel and Harish-Chandra's theorem [Reference Borel and Harish-ChandraBH62, theorem 9.4] because
$\mathcal {O}_M$ is finite by Borel and Harish-Chandra's theorem [Reference Borel and Harish-ChandraBH62, theorem 9.4] because ![]() $H$ is semi-simple, and the following lemma gives an estimate for its volume.
$H$ is semi-simple, and the following lemma gives an estimate for its volume.
Lemma 6.7
(i) Let
 $M$ be a positive-definite matrix of rank
$M$ be a positive-definite matrix of rank  $r\leq p$ represented by the lattice
$r\leq p$ represented by the lattice  $(V_\mathbb {Z},B)$. Then there exists
$(V_\mathbb {Z},B)$. Then there exists  $c>0$ depending only on
$c>0$ depending only on  $(V_\mathbb {Z},B)$ and
$(V_\mathbb {Z},B)$ and  $r$ such that
where for a prime number
$r$ such that
where for a prime number \[ a(M)\overset{\text{def}}=\operatorname{Vol}(\mathcal{O}_M)=c\det(M)^{({p+2q-r-1})/{2}}\prod_{a\,\text{prime}}\beta_a(M), \]
\[ a(M)\overset{\text{def}}=\operatorname{Vol}(\mathcal{O}_M)=c\det(M)^{({p+2q-r-1})/{2}}\prod_{a\,\text{prime}}\beta_a(M), \]
 $a$, the local density at
$a$, the local density at  $a$ is expressed as
$a$ is expressed as
 \[ \beta_{a}(M)\overset{\text{def}}=\lim_{s\rightarrow \infty}a^{-s(r(p+2q-({r+1})/{2}))}|\{\underline{\lambda}\in V_\mathbb{Z}^r/a^sV_\mathbb{Z}^r, I(\underline{\lambda})=M\}|. \]
\[ \beta_{a}(M)\overset{\text{def}}=\lim_{s\rightarrow \infty}a^{-s(r(p+2q-({r+1})/{2}))}|\{\underline{\lambda}\in V_\mathbb{Z}^r/a^sV_\mathbb{Z}^r, I(\underline{\lambda})=M\}|. \]
(ii) If
 $(M_n)_{n\in \mathbb {N}}$ is a sequence of positive-definite matrices primitively represented by
$(M_n)_{n\in \mathbb {N}}$ is a sequence of positive-definite matrices primitively represented by  $(V_\mathbb {Z},B)$, then
for any
$(V_\mathbb {Z},B)$, then
for any \[ a(M_n) \underset{n\to \infty}{\geq}\det(M_n)^{({p+2q-r-1})/{2}-\epsilon} \]
\[ a(M_n) \underset{n\to \infty}{\geq}\det(M_n)^{({p+2q-r-1})/{2}-\epsilon} \]
 $\epsilon >0$. In particular,
$\epsilon >0$. In particular,  $a(M_n)$ goes to
$a(M_n)$ goes to  $+\infty$, as
$+\infty$, as  $\det (M_n)$ goes to
$\det (M_n)$ goes to  $+\infty$.
$+\infty$.(iii) If, moreover,
 $r\leq ({p+2q-3})/{2}$, then
$r\leq ({p+2q-3})/{2}$, then
 \[ a(M_n) \underset{n\to \infty}{\asymp}\det(M_n)^{({p+2q-r-1})/{2}}. \]
\[ a(M_n) \underset{n\to \infty}{\asymp}\det(M_n)^{({p+2q-r-1})/{2}}. \]
Proof. The first assertion is simply the Siegel–Weil formula, which is valid in this setting by [Reference WeilWei62]. To prove the second statement, we need to find a lower bound on the growth of the product of the local densities ![]() $\beta _a(M_n)$ assuming that
$\beta _a(M_n)$ assuming that ![]() $M_n$ is primitively represented by
$M_n$ is primitively represented by ![]() $(V_\mathbb {Z}^r,B)$. Let
$(V_\mathbb {Z}^r,B)$. Let ![]() $n\in \mathbb {N}$ and let
$n\in \mathbb {N}$ and let ![]() $P(n)$ be the set of odd primes
$P(n)$ be the set of odd primes ![]() $a$ which are coprime to
$a$ which are coprime to ![]() $\det (M_n)\cdot\det (V_\mathbb {Z})$. By [Reference KitaokaKit93, Proposition 5.6.2(ii)], there exists two positive numbers
$\det (M_n)\cdot\det (V_\mathbb {Z})$. By [Reference KitaokaKit93, Proposition 5.6.2(ii)], there exists two positive numbers ![]() $c_1,c_2$ depending only on
$c_1,c_2$ depending only on ![]() $V_\mathbb {Z}$ such that
$V_\mathbb {Z}$ such that
If ![]() $r\leq ({p+2q-3})/{2}$, then by Corollary 5.6.2 [Reference KitaokaKit93], the above estimate on the product is true for
$r\leq ({p+2q-3})/{2}$, then by Corollary 5.6.2 [Reference KitaokaKit93], the above estimate on the product is true for ![]() $a$ ranging over all primes, proving the third statement.
$a$ ranging over all primes, proving the third statement.
Otherwise, because we assumed that ![]() $M_n$ is represented by a sublattice of
$M_n$ is represented by a sublattice of ![]() $V_\mathbb {Z}$ which is primitive,Footnote 7 then [Reference KitaokaKit93, Theorem 5.6.5,(a)] yields that there exists a constant
$V_\mathbb {Z}$ which is primitive,Footnote 7 then [Reference KitaokaKit93, Theorem 5.6.5,(a)] yields that there exists a constant ![]() $c_3<1$ such that for any prime
$c_3<1$ such that for any prime ![]() $a$ dividing
$a$ dividing ![]() $\det (V_\mathbb {Z})\cdot \det (M_n)$ we have
$\det (V_\mathbb {Z})\cdot \det (M_n)$ we have
As the number of prime divisors of ![]() $\det (M_n)$ is
$\det (M_n)$ is ![]() $O({\log (\det (M_n))}/{\log \log (\det (M_n))})$, we obtain that
$O({\log (\det (M_n))}/{\log \log (\det (M_n))})$, we obtain that
For a positive-definite integral matrix ![]() $M$, let
$M$, let ![]() $\mu _1(M)$ be the square root of the smallest non-zero integer represented by
$\mu _1(M)$ be the square root of the smallest non-zero integer represented by ![]() $M$.
$M$.
Theorem 6.8 Let ![]() $(M_n)_{n\in N}$ be a sequence of positive-definite matrices primitively represented by
$(M_n)_{n\in N}$ be a sequence of positive-definite matrices primitively represented by ![]() $(V_\mathbb {Z},B)$ and such that
$(V_\mathbb {Z},B)$ and such that ![]() $\mu _1(M_n)\rightarrow \infty$ as
$\mu _1(M_n)\rightarrow \infty$ as ![]() $n\rightarrow \infty$. Then the sequence of subsets
$n\rightarrow \infty$. Then the sequence of subsets ![]() $\{pr(W_{M_n}),n\in \mathbb {N}\}$ is equidistributed in
$\{pr(W_{M_n}),n\in \mathbb {N}\}$ is equidistributed in ![]() $V_{\mathbb {R},\mathrm {I}_r}^r$ in the sense of Theorem 2.16.
$V_{\mathbb {R},\mathrm {I}_r}^r$ in the sense of Theorem 2.16.
Proof. Note first that, because ![]() $M$ is positive definite, we have
$M$ is positive definite, we have ![]() $\det (M)\geq c \mu _1(M)^2$ where
$\det (M)\geq c \mu _1(M)^2$ where ![]() $c$ depends only on the rank of
$c$ depends only on the rank of ![]() $M$, see [Reference Eskin and KatznelsonEK95, Equation (5)]. Hence,
$M$, see [Reference Eskin and KatznelsonEK95, Equation (5)]. Hence, ![]() $\det (M)$ goes to
$\det (M)$ goes to ![]() $\infty$ and so does
$\infty$ and so does ![]() $\operatorname {Vol}(\mathcal {O}_{M_n})$ by Lemma 6.7.
$\operatorname {Vol}(\mathcal {O}_{M_n})$ by Lemma 6.7.
To prove the equidistribution, we apply Theorem 2.16. As ![]() $H$ is not contained in a proper parabolic subgroup, the sequence
$H$ is not contained in a proper parabolic subgroup, the sequence ![]() $\mathcal {O}_{M_n}$ has no loss of mass, and we need to prove that it is non-focused see (Definition 2.14). We are in the easy situation where any sequence of
$\mathcal {O}_{M_n}$ has no loss of mass, and we need to prove that it is non-focused see (Definition 2.14). We are in the easy situation where any sequence of ![]() $\Gamma$-orbits
$\Gamma$-orbits ![]() $\Gamma \cdot \underline \lambda _n \subset pr(W_{{M_n}})$ is non-focused.
$\Gamma \cdot \underline \lambda _n \subset pr(W_{{M_n}})$ is non-focused.
To prove this, assume by contradiction that, up to taking a subsequence, there exists a proper subgroup ![]() $H'$ of
$H'$ of ![]() $G$ defined over
$G$ defined over ![]() $\mathbb {Q}$, an element
$\mathbb {Q}$, an element ![]() $g\in G$ such that
$g\in G$ such that ![]() $gH^0g^{-1}\subset H'$ and a sequence
$gH^0g^{-1}\subset H'$ and a sequence ![]() $\underline \lambda _{n} \in \mathcal {E}_{M_{n}}$ such that
$\underline \lambda _{n} \in \mathcal {E}_{M_{n}}$ such that ![]() $pr(\underline \lambda _n)\in H' g Z(H^0)\cdot \underline pr(\lambda _0)\lambda _0$.
$pr(\underline \lambda _n)\in H' g Z(H^0)\cdot \underline pr(\lambda _0)\lambda _0$.
Set ![]() $V_n = \mathrm {Span}_\mathbb {R}(\underline \lambda _n)$ and let
$V_n = \mathrm {Span}_\mathbb {R}(\underline \lambda _n)$ and let ![]() $H_n \subset G$ be the subgroup fixing
$H_n \subset G$ be the subgroup fixing ![]() $V_n$. Then
$V_n$. Then ![]() $H_n$ is conjugate to
$H_n$ is conjugate to ![]() $H$ and contained in
$H$ and contained in ![]() $H'$ for all
$H'$ for all ![]() $n$ by assumption on
$n$ by assumption on ![]() $\underline \lambda _n$. In particular, by Lemma 6.9,
$\underline \lambda _n$. In particular, by Lemma 6.9, ![]() $H'$ preserves a rational subspace
$H'$ preserves a rational subspace ![]() $W$ contained in
$W$ contained in ![]() $V_0$. Hence, every
$V_0$. Hence, every ![]() $H_n$ preserves
$H_n$ preserves ![]() $W$. As the action of
$W$. As the action of ![]() $H_N$ on
$H_N$ on ![]() $V_n^\perp$ is irreducible, we deduce that
$V_n^\perp$ is irreducible, we deduce that ![]() $W\subset V_n$ for all
$W\subset V_n$ for all ![]() $n$.
$n$.
As ![]() $W$ is rational, it intersects
$W$ is rational, it intersects ![]() $V_\mathbb {Z}$ in a lattice which is contained in
$V_\mathbb {Z}$ in a lattice which is contained in ![]() $\mathrm {Span}_\mathbb {Z}(\underline \lambda _n)$ for all
$\mathrm {Span}_\mathbb {Z}(\underline \lambda _n)$ for all ![]() $n$ since
$n$ since ![]() $\mathrm {Span}_\mathbb {Z}(\underline \lambda _n)$ is primitive. This contradicts the assumption that
$\mathrm {Span}_\mathbb {Z}(\underline \lambda _n)$ is primitive. This contradicts the assumption that ![]() $\mu _1(M_n)\to +\infty$.
$\mu _1(M_n)\to +\infty$.
Lemma 6.9 Let ![]() $V_0$ be a positive-definite rational subspace of
$V_0$ be a positive-definite rational subspace of ![]() $V_\mathbb {Q}$, let
$V_\mathbb {Q}$, let ![]() $H_0$ be the subgroup of
$H_0$ be the subgroup of ![]() $G$ fixing
$G$ fixing ![]() $V_0$, and let
$V_0$, and let ![]() $H$ be a proper connected subgroup of
$H$ be a proper connected subgroup of ![]() $G$ defined over
$G$ defined over ![]() $\mathbb {Q}$ and containing
$\mathbb {Q}$ and containing ![]() $H_0$. Then
$H_0$. Then ![]() $H$ leaves invariant a rational subspace of
$H$ leaves invariant a rational subspace of ![]() $V_0$.
$V_0$.
Proof. As a representation of ![]() $H_0$, the Lie algebra
$H_0$, the Lie algebra ![]() $\mathfrak {g}$ decomposes orthogonally with respect to the Killing form as
$\mathfrak {g}$ decomposes orthogonally with respect to the Killing form as
where ![]() $\mathfrak {p} = \{u\in \mathfrak {g} \mid u(V_0)\subset V_0^\perp \}$ is isomorphic to
$\mathfrak {p} = \{u\in \mathfrak {g} \mid u(V_0)\subset V_0^\perp \}$ is isomorphic to ![]() $\operatorname {Hom}(V_0,V_0^\perp )$. Note that the representation of
$\operatorname {Hom}(V_0,V_0^\perp )$. Note that the representation of ![]() $H_0$ on
$H_0$ on ![]() $V_0^\perp$ is irreducible and
$V_0^\perp$ is irreducible and ![]() $H_0$ acts trivially on
$H_0$ acts trivially on ![]() $V_0$, hence also on
$V_0$, hence also on ![]() $\mathfrak {so}(V_0)$.
$\mathfrak {so}(V_0)$.
As ![]() $H$ contains
$H$ contains ![]() $H_0$, its Lie algebra
$H_0$, its Lie algebra ![]() $\mathfrak {h}$ is a subrepresentation of
$\mathfrak {h}$ is a subrepresentation of ![]() $\mathfrak {g}$ and, thus, decomposes as
$\mathfrak {g}$ and, thus, decomposes as
where ![]() $\mathfrak {k}$ is a Lie subalgebra of
$\mathfrak {k}$ is a Lie subalgebra of ![]() $\mathfrak {so}(V_0)$ and
$\mathfrak {so}(V_0)$ and ![]() $\mathfrak {p}'$ is a subrepresentation of
$\mathfrak {p}'$ is a subrepresentation of ![]() $\mathfrak {p} \simeq \operatorname {Hom}(V_0,V_0^\perp )$. By elementary representation theory, there exists a subspace
$\mathfrak {p} \simeq \operatorname {Hom}(V_0,V_0^\perp )$. By elementary representation theory, there exists a subspace ![]() $W\subset V_0$ such that
$W\subset V_0$ such that
We have
in particular, ![]() $W$ is a rational subspace because
$W$ is a rational subspace because ![]() $\mathfrak {h}$ and
$\mathfrak {h}$ and ![]() $V_0$ are defined over
$V_0$ are defined over ![]() $\mathbb {Q}$.
$\mathbb {Q}$.
We claim that ![]() $\mathfrak {k}$ preserves
$\mathfrak {k}$ preserves ![]() $W$. Indeed, assume by contradiction that there exists
$W$. Indeed, assume by contradiction that there exists ![]() $u\in \mathfrak {k}$ and
$u\in \mathfrak {k}$ and ![]() $x\in W$ such that
$x\in W$ such that ![]() $u(x)\in V_0\setminus W$. Then there is
$u(x)\in V_0\setminus W$. Then there is ![]() $v\in \mathfrak {p}'$ such that
$v\in \mathfrak {p}'$ such that ![]() $vu(x)\notin V_0$. As
$vu(x)\notin V_0$. As ![]() $v(x)=0$, we obtain that
$v(x)=0$, we obtain that
contradicting ![]() $x\in W$.
$x\in W$.
In conclusion, the Lie algebra ![]() $\mathfrak {h}$ preserves
$\mathfrak {h}$ preserves ![]() $W\subset V_0$. If
$W\subset V_0$. If ![]() $W$ were trivial, then we would have
$W$ were trivial, then we would have ![]() $\mathfrak {h} \supset \mathfrak {p}\oplus \mathfrak {h}_0$, hence
$\mathfrak {h} \supset \mathfrak {p}\oplus \mathfrak {h}_0$, hence ![]() $\mathfrak {h} = \mathfrak {g}$ because
$\mathfrak {h} = \mathfrak {g}$ because ![]() $[\mathfrak {p},\mathfrak {p}]\supset \mathfrak {so}(V_0)$. As
$[\mathfrak {p},\mathfrak {p}]\supset \mathfrak {so}(V_0)$. As ![]() $H$ is a proper subgroup,
$H$ is a proper subgroup, ![]() $W$ is non-trivial.
$W$ is non-trivial.
6.1.3 Proof of Theorems 1.6 and 1.7
Gathering together the results of the previous sections, we can finally prove our equidistribution theorems for refined Noether–Lefschetz loci in weight two. Let us first state them more precisely.
Let ![]() $\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a
$\{\mathbb {V}_\mathbb {Z},\mathcal {F}^\bullet \mathcal {V},B\}$ be a ![]() $\mathbb {Z}$-PVHS of weight two over a complex manifold
$\mathbb {Z}$-PVHS of weight two over a complex manifold ![]() $S$ of dimension
$S$ of dimension ![]() $rq$ as in Theorem 1.6. Let
$rq$ as in Theorem 1.6. Let ![]() $s\in S$ and let
$s\in S$ and let ![]() $P\subseteq \operatorname {Hdg}(s)$ be a subspace of rank
$P\subseteq \operatorname {Hdg}(s)$ be a subspace of rank ![]() $r$. Then the pair
$r$. Then the pair ![]() $(s,P)$ is a transverse intersection point of
$(s,P)$ is a transverse intersection point of ![]() $S$ with a
$S$ with a ![]() $H$-orbit, where
$H$-orbit, where ![]() $H$ is the stabilizer of a positive-definite subspace of
$H$ is the stabilizer of a positive-definite subspace of ![]() $V_\mathbb {R}$ as in § 6.1.1, if
$V_\mathbb {R}$ as in § 6.1.1, if ![]() $s$ does not admit first-order deformations such that
$s$ does not admit first-order deformations such that ![]() $P$ still embeds in the group of Hodge classes. Similarly, if
$P$ still embeds in the group of Hodge classes. Similarly, if ![]() $(\lambda _1,\ldots,\lambda _r)\in \operatorname {Hdg}(s)^r$ have intersection matrix
$(\lambda _1,\ldots,\lambda _r)\in \operatorname {Hdg}(s)^r$ have intersection matrix ![]() $M$, then the tuple
$M$, then the tuple ![]() $(s,\lambda _1,\ldots,\lambda _r)$ is a transverse intersection point with a
$(s,\lambda _1,\ldots,\lambda _r)$ is a transverse intersection point with a ![]() $H$-orbit,
$H$-orbit, ![]() $H$ being now the stabilizer of an orthonormal
$H$ being now the stabilizer of an orthonormal ![]() $r$-tuple as in § 6.1.2, if
$r$-tuple as in § 6.1.2, if ![]() $s$ does not admit first-order deformations such that
$s$ does not admit first-order deformations such that ![]() $\lambda _1,\ldots,\lambda _r$ all remain Hodge classes.
$\lambda _1,\ldots,\lambda _r$ all remain Hodge classes.
We can now prove the main theorems in § 1.2.1. Notation and hypothesis are as in Theorem 1.6.
Theorem 6.10 There exists a constant ![]() $\lambda >0$ such that, for every relatively compact open subset
$\lambda >0$ such that, for every relatively compact open subset ![]() $\Omega \subset S$ with boundary of measure
$\Omega \subset S$ with boundary of measure ![]() $0$, we have
$0$, we have
 \begin{align*} n^{-({p+2q})/{2}} \vert
\{(s,P)\mid s\in \Omega, P\subseteq
\operatorname{Hdg}(s), \operatorname{rank}(P)=r,
(s,P)\text{ regular}, \mathrm{disc}(P)\leq n \} \vert\\
\underset{n\to+\infty}{\longrightarrow} \lambda \int_\Omega
c_q(\mathcal{F}^2\mathcal{V})^r, \end{align*}
\begin{align*} n^{-({p+2q})/{2}} \vert
\{(s,P)\mid s\in \Omega, P\subseteq
\operatorname{Hdg}(s), \operatorname{rank}(P)=r,
(s,P)\text{ regular}, \mathrm{disc}(P)\leq n \} \vert\\
\underset{n\to+\infty}{\longrightarrow} \lambda \int_\Omega
c_q(\mathcal{F}^2\mathcal{V})^r, \end{align*}
where ![]() $c_q$ denotes the
$c_q$ denotes the ![]() $q$th Chern form of the bundle
$q$th Chern form of the bundle ![]() $\mathcal {F}^2\mathcal {V}$ endowed with the Hodge metric.
$\mathcal {F}^2\mathcal {V}$ endowed with the Hodge metric.
Proof. We use the notation from § 6.1.1. By Theorem 6.1, the sequence ![]() $(\mathcal {P}_n)_{n\in \mathbb {N}}$ is equidistributed in
$(\mathcal {P}_n)_{n\in \mathbb {N}}$ is equidistributed in ![]() $G/H$. We are now in the setting of Theorem 3.6. By Theorem 5.21, the pull–push form
$G/H$. We are now in the setting of Theorem 3.6. By Theorem 5.21, the pull–push form ![]() $\pi _*p^* \omega _{G/H}$ is equal to
$\pi _*p^* \omega _{G/H}$ is equal to ![]() $\operatorname {Vol}(G_U/H_U)\cdot c_q(\mathcal {F}^2\mathcal {V})^r$, where
$\operatorname {Vol}(G_U/H_U)\cdot c_q(\mathcal {F}^2\mathcal {V})^r$, where ![]() $c_q(\mathcal {F}^2\mathcal {V})$ is the
$c_q(\mathcal {F}^2\mathcal {V})$ is the ![]() $q$th Chern form of
$q$th Chern form of ![]() $\mathcal {F}^2\mathcal {V}$. We can hence apply Theorem 3.6 to deduce Theorem 1.7.
$\mathcal {F}^2\mathcal {V}$. We can hence apply Theorem 3.6 to deduce Theorem 1.7.
Notation and hypothesis are now as in Theorem 1.7.
Theorem 6.11 For every relatively compact open subset ![]() $\Omega \subset S$ with boundary of measure zero, we have
$\Omega \subset S$ with boundary of measure zero, we have
 \begin{align*}
\frac{1}{a(M_n)}|\{(s,\lambda_1,\ldots,\lambda_r))&\in
\Omega\times \mathbb{V}^r_{\mathbb{Z},s}\, \text{regular
tuple},(B(\lambda_i\cdot\lambda_j))_{1\leq i,j\leq r}=M_n,
\lambda_i \in \mathrm{Hdg}(s)\}|\\ &\underset{n\rightarrow
\infty}{\longrightarrow} \operatorname{Vol}(G_U/H_U)
\int_{\Omega}c_q(\mathcal{F}^2\mathcal{V})^r.
\end{align*}
\begin{align*}
\frac{1}{a(M_n)}|\{(s,\lambda_1,\ldots,\lambda_r))&\in
\Omega\times \mathbb{V}^r_{\mathbb{Z},s}\, \text{regular
tuple},(B(\lambda_i\cdot\lambda_j))_{1\leq i,j\leq r}=M_n,
\lambda_i \in \mathrm{Hdg}(s)\}|\\ &\underset{n\rightarrow
\infty}{\longrightarrow} \operatorname{Vol}(G_U/H_U)
\int_{\Omega}c_q(\mathcal{F}^2\mathcal{V})^r.
\end{align*}
Proof. We use the notation from § 6.1.2. By Theorem 6.8, the sequence ![]() $(pr(W_{M_n}))_{n\in \mathbb {N}}$ is equidistributed in
$(pr(W_{M_n}))_{n\in \mathbb {N}}$ is equidistributed in ![]() $G/H$. We are now again in the setting of Theorem 3.6. Here
$G/H$. We are now again in the setting of Theorem 3.6. Here ![]() $H$ is the stabilizer of an orthonormal
$H$ is the stabilizer of an orthonormal ![]() $r$-tuple of vectors, and if we denote by
$r$-tuple of vectors, and if we denote by ![]() $H'$ the stabilizer of the rank
$H'$ the stabilizer of the rank ![]() $r$ subspace they generate in
$r$ subspace they generate in ![]() $\mathbb {V}_\mathbb {R}$, then
$\mathbb {V}_\mathbb {R}$, then ![]() $H'/H$ is compact and one easily checks then that
$H'/H$ is compact and one easily checks then that ![]() $\pi _*p^* \omega _{G/H}=\operatorname {Vol}(H'/H)\pi _*p^* \omega _{G/H'}$.
$\pi _*p^* \omega _{G/H}=\operatorname {Vol}(H'/H)\pi _*p^* \omega _{G/H'}$.
By Theorem 5.21, the pull–push form ![]() $\pi _*p^*=\omega _{G/H'}$ is equal to
$\pi _*p^*=\omega _{G/H'}$ is equal to ![]() $\operatorname {Vol}(G_U/H'_U)\cdot c_q(\mathcal {F}^2\mathcal {V})^r$, where
$\operatorname {Vol}(G_U/H'_U)\cdot c_q(\mathcal {F}^2\mathcal {V})^r$, where ![]() $c_q(\mathcal {F}^2\mathcal {V})$ is the
$c_q(\mathcal {F}^2\mathcal {V})$ is the ![]() $q$th-Chern form of
$q$th-Chern form of ![]() $\mathcal {F}^2\mathcal {V}$. Moreover,
$\mathcal {F}^2\mathcal {V}$. Moreover,
Hence, ![]() $\pi _*p^* \omega _{G/H}=\operatorname {Vol}(G_U/H_U)c_q(\mathcal {F}^2\mathcal {V})^r$. We can hence apply Theorem 3.6 to deduce Theorem 1.7. Indeed, one can easily see again that regular points in our definition above correspond to transverse intersection points defined there.
$\pi _*p^* \omega _{G/H}=\operatorname {Vol}(G_U/H_U)c_q(\mathcal {F}^2\mathcal {V})^r$. We can hence apply Theorem 3.6 to deduce Theorem 1.7. Indeed, one can easily see again that regular points in our definition above correspond to transverse intersection points defined there.
Finally, we mention briefly how to prove Proposition 1.24.
6.2 Equidistribution of families of CM points in Shimura varieties
In this section, we use Theorem 1.1 to study the equidistribution of transverse intersection loci of Hecke correspondences on Shimura varieties and deduce the equidistribution of some families of CM points in average. We recall first the definition of a CM Hodge structure, see [Reference Green, Griffiths and KerrGGK12, V].
A CM field is a totally imaginary number field which is a quadratic extension of a totally real number field. A CM algebra is a finite product of CM number fields.
Definition 6.12 Let ![]() $(V,B,F^\bullet )$ be a pure polarized integral Hodge structure and let
$(V,B,F^\bullet )$ be a pure polarized integral Hodge structure and let ![]() $d=\operatorname {rank}_\mathbb {Z} V$. We say that
$d=\operatorname {rank}_\mathbb {Z} V$. We say that ![]() $(V,B,F^\bullet )$ has complex multiplication (‘CM’ for short) if one of the following equivalent conditions hold:
$(V,B,F^\bullet )$ has complex multiplication (‘CM’ for short) if one of the following equivalent conditions hold:
(i) its algebraic Mumford–Tate group
 $\mathrm {MT}_{\varphi }$ is a torus;
$\mathrm {MT}_{\varphi }$ is a torus;(ii) the ring
 $\mathrm {End}_\mathbb {Q}(V,F^\bullet )$ contains an étale CM subalgebra of dimension
$\mathrm {End}_\mathbb {Q}(V,F^\bullet )$ contains an étale CM subalgebra of dimension  $2d$.
$2d$.
We refer to [Reference Green, Griffiths and KerrGGK10, (IV.B.1)] for the equivalence in the definition.
Example 6.13 (i) Let ![]() $(A,\lambda )$ be a polarized complex abelian variety and let
$(A,\lambda )$ be a polarized complex abelian variety and let ![]() $\mathrm {End}(A)_\mathbb {Q}=\mathrm {End}(A)\otimes \mathbb {Q}$. Recall that
$\mathrm {End}(A)_\mathbb {Q}=\mathrm {End}(A)\otimes \mathbb {Q}$. Recall that ![]() $A$ has complex multiplication if
$A$ has complex multiplication if ![]() $\mathrm {End}_\mathbb {Q}(A)$ contains an étale subalgebra of degree
$\mathrm {End}_\mathbb {Q}(A)$ contains an étale subalgebra of degree ![]() $2\dim (A)$ over
$2\dim (A)$ over ![]() $\mathbb {Q}$. This is equivalent to the polarized Hodge structure
$\mathbb {Q}$. This is equivalent to the polarized Hodge structure ![]() $(H^1(X,\mathbb {Z}),\psi )$ being CM in the sense of Definition 6.12.
$(H^1(X,\mathbb {Z}),\psi )$ being CM in the sense of Definition 6.12.
(ii) Let ![]() $(X,\ell )$ be a complex polarized K3 surface and let
$(X,\ell )$ be a complex polarized K3 surface and let ![]() $T(X)$ be the transcendental lattice of
$T(X)$ be the transcendental lattice of ![]() $X$, i.e. the orthogonal complement of
$X$, i.e. the orthogonal complement of ![]() $\mathrm {Pic}(X)$ inside
$\mathrm {Pic}(X)$ inside ![]() $H^2(X,\mathbb {Z})$ with respect to the Poincaré form. Then
$H^2(X,\mathbb {Z})$ with respect to the Poincaré form. Then ![]() $X$ has CM if
$X$ has CM if ![]() $E\overset {\text {def}}=\mathrm {End}(T(X))_\mathbb {Q}$ is a CM field and
$E\overset {\text {def}}=\mathrm {End}(T(X))_\mathbb {Q}$ is a CM field and ![]() $T(X)_\mathbb {Q}$ is of dimension one over
$T(X)_\mathbb {Q}$ is of dimension one over ![]() $E$. If
$E$. If ![]() $PH^2(X,\mathbb {Z})$ is the primitive cohomology of
$PH^2(X,\mathbb {Z})$ is the primitive cohomology of ![]() $X$, then this is equivalent to
$X$, then this is equivalent to ![]() $PH^2(X,\mathbb {Z})$ being CM in the sense of Definition 6.12.
$PH^2(X,\mathbb {Z})$ being CM in the sense of Definition 6.12.
Let ![]() $(\widetilde {G},\mathcal {D})$ be a Shimura datum, see [Reference DeligneDel71, Reference DeligneDel79], and let
$(\widetilde {G},\mathcal {D})$ be a Shimura datum, see [Reference DeligneDel71, Reference DeligneDel79], and let ![]() $\mathcal {D}^+$ be a connected component of
$\mathcal {D}^+$ be a connected component of ![]() $\mathcal {D}$ ;
$\mathcal {D}$ ; ![]() $\mathcal {D}^+$ is a
$\mathcal {D}^+$ is a ![]() $\widetilde {G}^{\rm ad}(\mathbb {R})^+$-conjugacy class of a morphisms
$\widetilde {G}^{\rm ad}(\mathbb {R})^+$-conjugacy class of a morphisms ![]() $h^{\rm ad}:\mathbb {S}\rightarrow \widetilde {G}^{\rm ad}_\mathbb {R}$ and it is a Hermitian symmetric domain. Let
$h^{\rm ad}:\mathbb {S}\rightarrow \widetilde {G}^{\rm ad}_\mathbb {R}$ and it is a Hermitian symmetric domain. Let ![]() $K_\infty$ be the stabilizer of
$K_\infty$ be the stabilizer of ![]() $h^{\rm ad}(i)$ in
$h^{\rm ad}(i)$ in ![]() $\widetilde {G}^{\rm ad}(\mathbb {R})^+$. If
$\widetilde {G}^{\rm ad}(\mathbb {R})^+$. If ![]() $K_{\infty,+}$ is its preimage by the adjoint map, then we have an isomorphism
$K_{\infty,+}$ is its preimage by the adjoint map, then we have an isomorphism ![]() $\mathcal {D}^+=\widetilde {G}(\mathbb {R})_+/K_{\infty,+}\simeq \widetilde {G}^{\rm ad}(\mathbb {R})^+/K_\infty$. Let
$\mathcal {D}^+=\widetilde {G}(\mathbb {R})_+/K_{\infty,+}\simeq \widetilde {G}^{\rm ad}(\mathbb {R})^+/K_\infty$. Let ![]() $\Gamma \subset \widetilde {G}(\mathbb {Q})$ be an arithmetic subgroup and let
$\Gamma \subset \widetilde {G}(\mathbb {Q})$ be an arithmetic subgroup and let ![]() $X=\Gamma \backslash \mathcal {D}^+$. Then
$X=\Gamma \backslash \mathcal {D}^+$. Then ![]() $X$ is a (connected) Shimura variety.
$X$ is a (connected) Shimura variety.
Definition 6.14 Let ![]() $g\in \widetilde {G}^{\rm ad}(\mathbb {Q})$ and
$g\in \widetilde {G}^{\rm ad}(\mathbb {Q})$ and ![]() $\Gamma _g=g^{-1}\Gamma g\cap \Gamma$. The Hecke correspondence
$\Gamma _g=g^{-1}\Gamma g\cap \Gamma$. The Hecke correspondence ![]() $\mathcal {C}_g\hookrightarrow X\times X$ is the image of
$\mathcal {C}_g\hookrightarrow X\times X$ is the image of ![]() $\Gamma _g\backslash \mathcal {D}$ by the embedding
$\Gamma _g\backslash \mathcal {D}$ by the embedding
If ![]() $g=1$ is the identity of
$g=1$ is the identity of ![]() $\widetilde {G}(\mathbb {Q})$, then
$\widetilde {G}(\mathbb {Q})$, then ![]() $\mathcal {C}_1$ is simply the diagonal embedding of
$\mathcal {C}_1$ is simply the diagonal embedding of ![]() $X$ in
$X$ in ![]() $X\times X$.
$X\times X$.
Proposition 6.15 For ![]() $f\in \widetilde {G}(\mathbb {R})$, the following properties are equivalent:
$f\in \widetilde {G}(\mathbb {R})$, the following properties are equivalent:
(i)
 $f$ has a unique fixed point in
$f$ has a unique fixed point in  $\mathcal {D}$;
$\mathcal {D}$;(ii) the centralizer of
 $f$ is compact in
$f$ is compact in  $\widetilde {G}^{\rm ad}(\mathbb {R})$;
$\widetilde {G}^{\rm ad}(\mathbb {R})$;(iii) the intersection of the graph of
 $f$ and the diagonal in
$f$ and the diagonal in  $\mathcal {D}\times \mathcal {D}$ is transversal and non-empty.
$\mathcal {D}\times \mathcal {D}$ is transversal and non-empty.
If ![]() $f$ satisfies those properties, we say that
$f$ satisfies those properties, we say that ![]() $f$ is regular.
$f$ is regular.
Proof. (i)![]() $\Rightarrow$(ii). Let
$\Rightarrow$(ii). Let ![]() $x$ be the unique fixed point of
$x$ be the unique fixed point of ![]() $f$, then
$f$, then ![]() $f$ is contained in the stabilizer of
$f$ is contained in the stabilizer of ![]() $x$ in
$x$ in ![]() $\widetilde {G}^{\rm ad}(\mathbb {R})$ which is a compact subgroup. Moreover, for any
$\widetilde {G}^{\rm ad}(\mathbb {R})$ which is a compact subgroup. Moreover, for any ![]() $g\in Z(f)$,
$g\in Z(f)$, ![]() $g\cdot x$ is also a fixed point for
$g\cdot x$ is also a fixed point for ![]() $f$, hence equal to
$f$, hence equal to ![]() $x$ and thus
$x$ and thus ![]() $Z(f)\subseteq K$.
$Z(f)\subseteq K$.
(ii)![]() $\Rightarrow$(iii). As
$\Rightarrow$(iii). As ![]() $Z(f)$ is compact, it is contained in a maximal compact subgroup
$Z(f)$ is compact, it is contained in a maximal compact subgroup ![]() $K$ of
$K$ of ![]() $\widetilde {G}^{\rm ad}(\mathbb {R})$. Hence,
$\widetilde {G}^{\rm ad}(\mathbb {R})$. Hence, ![]() $f$ fixes a point
$f$ fixes a point ![]() $x$ and the differential
$x$ and the differential ![]() $df_x$ on
$df_x$ on ![]() $T_x\mathcal {D}$ identifies to the action of
$T_x\mathcal {D}$ identifies to the action of ![]() $Ad(f)$ on
$Ad(f)$ on ![]() $\mathfrak {p}$, the orthogonal complement of
$\mathfrak {p}$, the orthogonal complement of ![]() $\mathfrak {p}$ in
$\mathfrak {p}$ in ![]() $\widetilde {\mathfrak {g}}^{\rm ad}$ with respect to the Killing form. Then
$\widetilde {\mathfrak {g}}^{\rm ad}$ with respect to the Killing form. Then ![]() $Ad(f)$ does not have
$Ad(f)$ does not have ![]() $1$ as eigenvalue in
$1$ as eigenvalue in ![]() $\mathfrak {p}$, as
$\mathfrak {p}$, as ![]() $Z(f)\subseteq K$. This will hold true at any fixed point
$Z(f)\subseteq K$. This will hold true at any fixed point ![]() $f$ in
$f$ in ![]() $\mathcal {D}$. Let
$\mathcal {D}$. Let ![]() $(x,x)$ be an intersection point of the graph
$(x,x)$ be an intersection point of the graph ![]() $\mathcal {C}_f$ of
$\mathcal {C}_f$ of ![]() $f$ and the diagonal
$f$ and the diagonal ![]() $\Delta$ in
$\Delta$ in ![]() $\mathcal {D}\times \mathcal {D}$, then the tangent spaces of
$\mathcal {D}\times \mathcal {D}$, then the tangent spaces of ![]() $\mathcal {C}_f$ and
$\mathcal {C}_f$ and ![]() $\Delta$ at
$\Delta$ at ![]() $(x,x)=(x,f\cdot x)$ inside
$(x,x)=(x,f\cdot x)$ inside ![]() $T_{(x,x)}(\mathcal {D}\times \mathcal {D})$ are given by
$T_{(x,x)}(\mathcal {D}\times \mathcal {D})$ are given by ![]() $\{(X,X)\mid X\in \mathfrak {p}\}$ and
$\{(X,X)\mid X\in \mathfrak {p}\}$ and ![]() $\{(X,Ad(f)\cdot X)\mid X\in \mathfrak {p}\}$, respectively. Their sum is equal to
$\{(X,Ad(f)\cdot X)\mid X\in \mathfrak {p}\}$, respectively. Their sum is equal to ![]() $\mathfrak {p}\oplus {\mathfrak {p}}$ if and only if their intersection is zero, which is true as
$\mathfrak {p}\oplus {\mathfrak {p}}$ if and only if their intersection is zero, which is true as ![]() $1$ is not an eigenvalue of
$1$ is not an eigenvalue of ![]() $Ad(f)$ in
$Ad(f)$ in ![]() $\mathfrak {p}$.
$\mathfrak {p}$.
(iii)![]() $\Rightarrow$(i). If the intersection is transverse, then by the previous computation, for any fixed
$\Rightarrow$(i). If the intersection is transverse, then by the previous computation, for any fixed ![]() $x$ point of
$x$ point of ![]() $f$, the eigenvalues of
$f$, the eigenvalues of ![]() $df_x$ in
$df_x$ in ![]() $\mathfrak {p}$ are different from
$\mathfrak {p}$ are different from ![]() $1$. If
$1$. If ![]() $f$ fixes another point
$f$ fixes another point ![]() $y\in \mathcal {D}$, then it fixes the geodesic line
$y\in \mathcal {D}$, then it fixes the geodesic line ![]() $\gamma :\mathbb {R}\rightarrow \mathcal {D}$ linking
$\gamma :\mathbb {R}\rightarrow \mathcal {D}$ linking ![]() $\gamma (0)=x$ to
$\gamma (0)=x$ to ![]() $y$ and, hence, acts trivially on this line. Hence,
$y$ and, hence, acts trivially on this line. Hence, ![]() $df_x(\dot {\gamma }(0))=\dot {\gamma }(0)$ which is a contradiction. Thus,
$df_x(\dot {\gamma }(0))=\dot {\gamma }(0)$ which is a contradiction. Thus, ![]() $f$ has a unique fixed point.
$f$ has a unique fixed point.
Lemma 6.16 A point ![]() $[x] \in X$ is CM if and only if there exists
$[x] \in X$ is CM if and only if there exists ![]() $g\in \widetilde {G}(\mathbb {Q})$ such that
$g\in \widetilde {G}(\mathbb {Q})$ such that ![]() $\mathcal {C}_1$ and
$\mathcal {C}_1$ and ![]() $\mathcal {C}_g$ intersect transversally at
$\mathcal {C}_g$ intersect transversally at ![]() $x$.
$x$.
Proof. The transverse intersection locus of ![]() $\mathcal {C}_g$ and
$\mathcal {C}_g$ and ![]() $\mathcal {C}_1$ inside
$\mathcal {C}_1$ inside ![]() $X\times X$ is necessarily of dimension zero by dimension count. Let
$X\times X$ is necessarily of dimension zero by dimension count. Let ![]() $[x]$ be a point in this intersection and
$[x]$ be a point in this intersection and ![]() $h_x:\mathbb {S}\rightarrow \widetilde {G}(\mathbb {R})$ a lift to
$h_x:\mathbb {S}\rightarrow \widetilde {G}(\mathbb {R})$ a lift to ![]() $\mathcal {D}$. Then there exists
$\mathcal {D}$. Then there exists ![]() $y \in \mathcal {D}$,
$y \in \mathcal {D}$, ![]() $\gamma _1,\gamma _2\in \Gamma$ such that
$\gamma _1,\gamma _2\in \Gamma$ such that ![]() $x=\gamma _1\cdot y$ and
$x=\gamma _1\cdot y$ and ![]() $x=\gamma _2g\cdot y$. Hence,
$x=\gamma _2g\cdot y$. Hence, ![]() $x=\gamma _2g\gamma _{1}^{-1}\cdot x$ which implies that
$x=\gamma _2g\gamma _{1}^{-1}\cdot x$ which implies that ![]() $MT(x)\subseteq Z(\gamma _2g\gamma _{1}^{-1})$. As the intersection is transverse at
$MT(x)\subseteq Z(\gamma _2g\gamma _{1}^{-1})$. As the intersection is transverse at ![]() $x$, then by the previous lemma,
$x$, then by the previous lemma, ![]() $\gamma _2g\gamma _{1}^{-1}$ is regular and contained in
$\gamma _2g\gamma _{1}^{-1}$ is regular and contained in ![]() $K$ by regularity. Hence, by [Reference Green, Griffiths and KerrGGK10, IV.B.1],
$K$ by regularity. Hence, by [Reference Green, Griffiths and KerrGGK10, IV.B.1], ![]() $x$ is a CM point.
$x$ is a CM point.
Conversely, let ![]() $x\in \mathcal {D}$ be a CM point. Then
$x\in \mathcal {D}$ be a CM point. Then ![]() $L\overset {\text {def}}= Z(MT(x))^{\circ }$, the connected component of the Mumford–Tate group in its centralizer, is defined over
$L\overset {\text {def}}= Z(MT(x))^{\circ }$, the connected component of the Mumford–Tate group in its centralizer, is defined over ![]() $\mathbb {Q}$. Then
$\mathbb {Q}$. Then ![]() $L(\mathbb {R})\subset K$ and the function
$L(\mathbb {R})\subset K$ and the function ![]() $u:f\mapsto \det (Ad(f)_{\vert \mathfrak p}-\mathrm {Id}_{\mathfrak {p}})$ is well defined and does not vanish as
$u:f\mapsto \det (Ad(f)_{\vert \mathfrak p}-\mathrm {Id}_{\mathfrak {p}})$ is well defined and does not vanish as ![]() $u(h_x(i))\neq 0$. By [Reference BorelBor91, § 18, Corollary 18.3],
$u(h_x(i))\neq 0$. By [Reference BorelBor91, § 18, Corollary 18.3], ![]() $L(\mathbb {Q})$ is Zariski dense in
$L(\mathbb {Q})$ is Zariski dense in ![]() $L(\mathbb {R})$, hence there exists an element
$L(\mathbb {R})$, hence there exists an element ![]() $f\in L(\mathbb {Q})$ which is regular and
$f\in L(\mathbb {Q})$ which is regular and ![]() $MT(x)\subseteq Z(f)$. Hence,
$MT(x)\subseteq Z(f)$. Hence, ![]() $x$ is a transverse intersection point of
$x$ is a transverse intersection point of ![]() $\mathcal {C}_f$ and
$\mathcal {C}_f$ and ![]() $\mathcal {C}_1$.
$\mathcal {C}_1$.
For ![]() $g\in \widetilde {G}^{\rm ad}(\mathbb {Q})$, let
$g\in \widetilde {G}^{\rm ad}(\mathbb {Q})$, let ![]() $\deg (g)=[\Gamma :\Gamma _g]$. More generally, if
$\deg (g)=[\Gamma :\Gamma _g]$. More generally, if ![]() $V\subset \widetilde {G}^{\rm ad}(\mathbb {Q})$ is a
$V\subset \widetilde {G}^{\rm ad}(\mathbb {Q})$ is a ![]() $\Gamma$-double class with finitely many left
$\Gamma$-double class with finitely many left ![]() $\Gamma$-orbits, we let
$\Gamma$-orbits, we let ![]() $\deg (V)$ be the number of distinct left
$\deg (V)$ be the number of distinct left ![]() $\Gamma$-orbits, in particular
$\Gamma$-orbits, in particular ![]() $\deg (g)=\deg (\Gamma g\Gamma )$. If we set
$\deg (g)=\deg (\Gamma g\Gamma )$. If we set ![]() $G\overset {\text {def}}= \widetilde {G}^{\rm ad}(\mathbb {R})^+\times \widetilde {G}^{\rm ad}(\mathbb {R})^+$ and
$G\overset {\text {def}}= \widetilde {G}^{\rm ad}(\mathbb {R})^+\times \widetilde {G}^{\rm ad}(\mathbb {R})^+$ and ![]() $H=\widetilde {G}^{\rm ad}(\mathbb {R})^+$ embedded diagonally in
$H=\widetilde {G}^{\rm ad}(\mathbb {R})^+$ embedded diagonally in ![]() $G$, then
$G$, then ![]() $G/H\simeq \widetilde {G}^{\rm ad}(\mathbb {R})$ and we are in the situation of § 2.5. Then we denote by
$G/H\simeq \widetilde {G}^{\rm ad}(\mathbb {R})$ and we are in the situation of § 2.5. Then we denote by ![]() $\mathcal {O}\subset (\Gamma \times \Gamma )\backslash G$ the corresponding finite union of closed
$\mathcal {O}\subset (\Gamma \times \Gamma )\backslash G$ the corresponding finite union of closed ![]() $H$-orbits and by
$H$-orbits and by ![]() $\mathcal {C}_{\mathcal {O}}\hookrightarrow X\times X$ the associated Hecke correspondence.
$\mathcal {C}_{\mathcal {O}}\hookrightarrow X\times X$ the associated Hecke correspondence.
Theorem 6.17 Let ![]() $X$ be a Shimura variety associated with a Shimura datum
$X$ be a Shimura variety associated with a Shimura datum ![]() $(\widetilde {G},\mathcal {D})$ such that
$(\widetilde {G},\mathcal {D})$ such that ![]() $\widetilde {G}^{\rm ad}$ is connected and
$\widetilde {G}^{\rm ad}$ is connected and ![]() $\mathbb {Q}$-simple. Let
$\mathbb {Q}$-simple. Let ![]() $(V_n)_{n\in \mathbb {N}}$ be a sequence of
$(V_n)_{n\in \mathbb {N}}$ be a sequence of ![]() $\Gamma$-double classes in
$\Gamma$-double classes in ![]() $\widetilde {G}(\mathbb {Q})$ such that
$\widetilde {G}(\mathbb {Q})$ such that ![]() $\deg (V_n)\rightarrow \infty$. Then for every
$\deg (V_n)\rightarrow \infty$. Then for every ![]() $\Omega \subset X$ open relatively compact subset with zero measure boundary
$\Omega \subset X$ open relatively compact subset with zero measure boundary
 \[ |\{(x,f)\mid x\in \Omega, f\in V_n, MT(x) \subset Z(f), f \text{ regular}\}|\underset{n\rightarrow \infty}{\sim}\frac{\deg(V_n)\cdot \chi(\widehat{\mathcal{D}})}{\operatorname{Vol}(\widehat{\mathcal{D}})}\int_{\Omega}\omega_\mathcal{D}. \]
\[ |\{(x,f)\mid x\in \Omega, f\in V_n, MT(x) \subset Z(f), f \text{ regular}\}|\underset{n\rightarrow \infty}{\sim}\frac{\deg(V_n)\cdot \chi(\widehat{\mathcal{D}})}{\operatorname{Vol}(\widehat{\mathcal{D}})}\int_{\Omega}\omega_\mathcal{D}. \]
Proof. Let ![]() $H=\widetilde {G}^{\rm ad}\hookrightarrow G\overset {\text {def}}= \widetilde {G}^{\rm ad}\times \widetilde {G}^{\rm ad}$ and, by assumption,
$H=\widetilde {G}^{\rm ad}\hookrightarrow G\overset {\text {def}}= \widetilde {G}^{\rm ad}\times \widetilde {G}^{\rm ad}$ and, by assumption, ![]() $\widetilde {G}^{\rm ad}$ is simple. Then the quotient
$\widetilde {G}^{\rm ad}$ is simple. Then the quotient ![]() $G/H$ is isomorphic to
$G/H$ is isomorphic to ![]() $H$ via the map
$H$ via the map ![]() $p:(x,y)\mapsto yx^{-1}$. The preimage by
$p:(x,y)\mapsto yx^{-1}$. The preimage by ![]() $p$ of an element
$p$ of an element ![]() $a\in G$ is equal to
$a\in G$ is equal to ![]() $(1,a)\cdot H\hookrightarrow G$.
$(1,a)\cdot H\hookrightarrow G$.
Then the sequence of ![]() $\Gamma$-double class
$\Gamma$-double class ![]() $(V_n)_{n\mathbb {N}}$ are equidistributed in
$(V_n)_{n\mathbb {N}}$ are equidistributed in ![]() $G/H$. This result has been proved by [Reference Clozel, Oh and UllmoCOU01] in the following cases:
$G/H$. This result has been proved by [Reference Clozel, Oh and UllmoCOU01] in the following cases: ![]() $\widetilde {G}$ is connected, almost simple simply connected and
$\widetilde {G}$ is connected, almost simple simply connected and ![]() $\text {rank}_\mathbb {Q}(\widetilde {G})\geq 1$ [Reference Clozel, Oh and UllmoCOU01, Theorem 1.6]) and for
$\text {rank}_\mathbb {Q}(\widetilde {G})\geq 1$ [Reference Clozel, Oh and UllmoCOU01, Theorem 1.6]) and for ![]() $G=\mathrm {GSp}_{2g}$ [Reference Clozel, Oh and UllmoCOU01, Remark (3), p. 332]. More generally, Eskin and Oh [Reference Eskin and OhEO06a] proved this result for any
$G=\mathrm {GSp}_{2g}$ [Reference Clozel, Oh and UllmoCOU01, Remark (3), p. 332]. More generally, Eskin and Oh [Reference Eskin and OhEO06a] proved this result for any ![]() $\widetilde {G}$ connected and simple over
$\widetilde {G}$ connected and simple over ![]() $\mathbb {Q}$.Footnote 8 Hence, we are in the setting of Theorem 1.1.
$\mathbb {Q}$.Footnote 8 Hence, we are in the setting of Theorem 1.1.
By Theorem 5.22, the restriction of the form ![]() $\pi _*p^*\omega _{G/H}$ to
$\pi _*p^*\omega _{G/H}$ to ![]() $\mathcal {D}$ is equal to
$\mathcal {D}$ is equal to ![]() ${\chi (\widehat {\mathcal {D}})}/{\operatorname {Vol}(\widehat {\mathcal {D}})}\cdot \omega _{\mathcal {D}}$. Hence, by Proposition 5.9,
${\chi (\widehat {\mathcal {D}})}/{\operatorname {Vol}(\widehat {\mathcal {D}})}\cdot \omega _{\mathcal {D}}$. Hence, by Proposition 5.9, ![]() $\Gamma \backslash \mathcal {D}$ is generically transverse to
$\Gamma \backslash \mathcal {D}$ is generically transverse to ![]() $H$-orbits and by Theorem 1.1, the transverse intersection locus of
$H$-orbits and by Theorem 1.1, the transverse intersection locus of ![]() $\mathcal {C}_{V_n}$ with
$\mathcal {C}_{V_n}$ with ![]() $X=\mathcal {C}_1$ is equidistributed in
$X=\mathcal {C}_1$ is equidistributed in ![]() $X$ with respect to
$X$ with respect to ![]() ${\chi (\widehat {\mathcal {D}})}/{\operatorname {Vol}(\widehat {\mathcal {D}})}\cdot \omega _{\mathcal {D}}$ as
${\chi (\widehat {\mathcal {D}})}/{\operatorname {Vol}(\widehat {\mathcal {D}})}\cdot \omega _{\mathcal {D}}$ as ![]() $n\rightarrow \infty$. By Lemma 6.16, this transverse locus is formed by elements
$n\rightarrow \infty$. By Lemma 6.16, this transverse locus is formed by elements ![]() $x$ where
$x$ where ![]() $x$ is a CM point with Mumford–Tate group
$x$ is a CM point with Mumford–Tate group ![]() $MT(x)\subset Z(f)$ where
$MT(x)\subset Z(f)$ where ![]() $f$ is regular and
$f$ is regular and ![]() $f\in V_n$. Hence, the result.
$f\in V_n$. Hence, the result.
In this next section, we give examples in situations where the Shimura variety ![]() $X$ receives an immersive dense map from a moduli space of algebraic varieties, namely principally polarized abelian varieties and polarized K3 surfaces.
$X$ receives an immersive dense map from a moduli space of algebraic varieties, namely principally polarized abelian varieties and polarized K3 surfaces.
6.2.1 Equidistribution in average of CM abelian varieties
We now apply Theorem 6.17 to study equidistribution of CM principally polarized abelian varieties. Let ![]() $g\geq 1$,
$g\geq 1$, ![]() $\widetilde {G}=GSp_{2g}$ the standard symplectic group over
$\widetilde {G}=GSp_{2g}$ the standard symplectic group over ![]() $\mathbb {Q}$ and
$\mathbb {Q}$ and ![]() $\mathbb {H}_g$ the Siegel upper half-space. Then
$\mathbb {H}_g$ the Siegel upper half-space. Then ![]() $(\widetilde {G},\mathbb {H}_g)$ is a Shimura datum and for
$(\widetilde {G},\mathbb {H}_g)$ is a Shimura datum and for ![]() $\Gamma =\mathrm {Sp}(2g,\mathbb {Z})$, the quotient
$\Gamma =\mathrm {Sp}(2g,\mathbb {Z})$, the quotient ![]() $\mathcal {A}_g\overset {\text {def}}= \Gamma \backslash \mathbb {H}_g$ is in bijection with the set of isomorphism classes of principally polarized abelian varieties over
$\mathcal {A}_g\overset {\text {def}}= \Gamma \backslash \mathbb {H}_g$ is in bijection with the set of isomorphism classes of principally polarized abelian varieties over ![]() $\mathbb {C}$.
$\mathbb {C}$.
For every ![]() $N\geq 1$, we have a double class
$N\geq 1$, we have a double class ![]() $V_N=\{f\in \mathrm {GL}_{2g}(\mathbb {Z})\cap \widetilde {G}(\mathbb {Q}), f^{\dagger} \circ f=N\cdot \mathrm {Id}\}$ where
$V_N=\{f\in \mathrm {GL}_{2g}(\mathbb {Z})\cap \widetilde {G}(\mathbb {Q}), f^{\dagger} \circ f=N\cdot \mathrm {Id}\}$ where ![]() $f^{\dagger}$ is the adjoint with respect to the symplectic form. The Hecke correspondence
$f^{\dagger}$ is the adjoint with respect to the symplectic form. The Hecke correspondence ![]() $\mathcal {C}_N$ given by this double class has the following modular interpretation:
$\mathcal {C}_N$ given by this double class has the following modular interpretation: ![]() $\mathcal {C}_N\hookrightarrow \mathcal {A}_g\times \mathcal {A}_g$ is the moduli of pairs
$\mathcal {C}_N\hookrightarrow \mathcal {A}_g\times \mathcal {A}_g$ is the moduli of pairs ![]() $(A_1,A_2,f)$ where
$(A_1,A_2,f)$ where ![]() $(A_1,A_2)$ are principally polarized abelian varieties of dimension
$(A_1,A_2)$ are principally polarized abelian varieties of dimension ![]() $g\geq 1$ and
$g\geq 1$ and ![]() $f:A_1\rightarrow A_2$ is an isogeny satisfying
$f:A_1\rightarrow A_2$ is an isogeny satisfying ![]() $f^{\dagger} \circ f =N\cdot \mathrm {Id}_{A_1}$ where
$f^{\dagger} \circ f =N\cdot \mathrm {Id}_{A_1}$ where ![]() $f^{\dagger} :B\rightarrow A$ is the dual isogeny. Note that
$f^{\dagger} :B\rightarrow A$ is the dual isogeny. Note that ![]() $\mathcal {C}_1$ is the diagonal embedding of
$\mathcal {C}_1$ is the diagonal embedding of ![]() $\mathcal {A}_g$ in
$\mathcal {A}_g$ in ![]() $\mathcal {A}_g\times \mathcal {A}_g$. In this context, the transverse intersection locus of
$\mathcal {A}_g\times \mathcal {A}_g$. In this context, the transverse intersection locus of ![]() $\mathcal {C}_N$ with
$\mathcal {C}_N$ with ![]() $\mathcal {C}_1$ corresponds to principally polarized CM abelian varieties
$\mathcal {C}_1$ corresponds to principally polarized CM abelian varieties ![]() $A$ endowed with an isogeny
$A$ endowed with an isogeny ![]() $f:A\rightarrow A$ whose homology class is a regular element of
$f:A\rightarrow A$ whose homology class is a regular element of ![]() $\widetilde {G}(\mathbb {R})$ and lies in
$\widetilde {G}(\mathbb {R})$ and lies in ![]() $V_N$. Then the Mumford–Tate group of
$V_N$. Then the Mumford–Tate group of ![]() $A$ is a subgroup of
$A$ is a subgroup of ![]() $Z(f)$.
$Z(f)$.
Lemma 6.18 The transverse intersection loci of ![]() $\mathcal {C}_N$ and
$\mathcal {C}_N$ and ![]() $\mathcal {C}_1$ is set-theoretically formed by triples
$\mathcal {C}_1$ is set-theoretically formed by triples ![]() $(A,\lambda,f)$ where
$(A,\lambda,f)$ where ![]() $(A,\lambda )$ is a principally polarized abelian variety,
$(A,\lambda )$ is a principally polarized abelian variety, ![]() $f:A\rightarrow A$ is an isogeny whose homological realization is regular and lies in
$f:A\rightarrow A$ is an isogeny whose homological realization is regular and lies in ![]() $V_N$ and
$V_N$ and ![]() $MT(A)\subseteq Z(f)$. In particular,
$MT(A)\subseteq Z(f)$. In particular, ![]() $A$ is a CM abelian variety.
$A$ is a CM abelian variety.
By applying Theorem 6.17, we obtain Theorem 1.21 from the introduction.
6.2.2 Equidistribution in average of CM K3 surfaces
We now discuss the second example which is the equidistribution of CM points in the moduli space of polarized K3 surfaces. Let ![]() $d\geq 1$ and let
$d\geq 1$ and let ![]() $\mathcal {F}_{2d}$ be the moduli space of complex polarized K3 surfaces of degree
$\mathcal {F}_{2d}$ be the moduli space of complex polarized K3 surfaces of degree ![]() $2d$. Then
$2d$. Then ![]() $\mathcal {F}_{2d}$ can be embedded into an orthogonal Shimura variety which is given as follows. Let
$\mathcal {F}_{2d}$ can be embedded into an orthogonal Shimura variety which is given as follows. Let ![]() $V_{K3}$ be the K3 lattice,
$V_{K3}$ be the K3 lattice, ![]() $V_{K3}=U^{3}\oplus E_{8}(-1)^2$,
$V_{K3}=U^{3}\oplus E_{8}(-1)^2$, ![]() $\ell _{2d}\in V_{K3}$ a primitive class of self-intersection
$\ell _{2d}\in V_{K3}$ a primitive class of self-intersection ![]() $2d$ (it is unique up to the action of
$2d$ (it is unique up to the action of ![]() $\mathrm {O}(V_{K3})$) and let
$\mathrm {O}(V_{K3})$) and let ![]() $V_{2d}=\ell _{2d}^{\bot }$. Let
$V_{2d}=\ell _{2d}^{\bot }$. Let ![]() $\widetilde {G}=\mathrm {GO}(V_{2d})$ and
$\widetilde {G}=\mathrm {GO}(V_{2d})$ and ![]() $\mathcal {D}=\{x\in \mathbb {P}(V_{2d,\mathbb {C}}, (x,x)=0, (x,\overline {x})=0)\}$. Then
$\mathcal {D}=\{x\in \mathbb {P}(V_{2d,\mathbb {C}}, (x,x)=0, (x,\overline {x})=0)\}$. Then ![]() $(G,\mathcal {D})$ is a Shimura datum and for
$(G,\mathcal {D})$ is a Shimura datum and for ![]() $\Gamma =\mathrm {Ker}(\mathrm {O}(V_{2d})\rightarrow \mathrm {O}(V^{\vee }_{2d}/V_{2d}))$, we have a period map
$\Gamma =\mathrm {Ker}(\mathrm {O}(V_{2d})\rightarrow \mathrm {O}(V^{\vee }_{2d}/V_{2d}))$, we have a period map ![]() $\mathcal {F}_{2d}\rightarrow \Gamma \backslash \mathcal {D}$ which is a local embedding by Torelli theorem [Reference HuybrechtsHuy16] and the complement of the image is a finite union of Cartier divisors. Under this map, K3 surfaces with CM, in the sense of [Reference HuybrechtsHuy16, Remark 3.10] correspond to CM points of the orthogonal Shimura variety
$\mathcal {F}_{2d}\rightarrow \Gamma \backslash \mathcal {D}$ which is a local embedding by Torelli theorem [Reference HuybrechtsHuy16] and the complement of the image is a finite union of Cartier divisors. Under this map, K3 surfaces with CM, in the sense of [Reference HuybrechtsHuy16, Remark 3.10] correspond to CM points of the orthogonal Shimura variety ![]() $\Gamma \backslash \mathcal {D}$. Let
$\Gamma \backslash \mathcal {D}$. Let ![]() $\omega _{\mathcal {D}}$ be the volume form on
$\omega _{\mathcal {D}}$ be the volume form on ![]() $\mathcal {D}$ as in § 2.3, and for
$\mathcal {D}$ as in § 2.3, and for ![]() $N\geq 1$, let
$N\geq 1$, let ![]() $V_N$ be the double class of integral elements
$V_N$ be the double class of integral elements ![]() $f\in \widetilde {G}(\mathbb {Q})$ which scale the bilinear form by
$f\in \widetilde {G}(\mathbb {Q})$ which scale the bilinear form by ![]() $N$.
$N$.
Theorem 6.19 Let ![]() $N\geq 1$ and let
$N\geq 1$ and let ![]() $CM(N)$ be the set of pairs
$CM(N)$ be the set of pairs ![]() $(X,\ell _{2d},f)$ where
$(X,\ell _{2d},f)$ where ![]() $(X,\ell _{2d})$ is a CM polarized K3 surface of degree
$(X,\ell _{2d})$ is a CM polarized K3 surface of degree ![]() $2d$,
$2d$, ![]() $f\in End(PH^2(X,\mathbb {Z}))$ is an isogeny with
$f\in End(PH^2(X,\mathbb {Z}))$ is an isogeny with ![]() $f^{\dagger} \circ f=N$, and
$f^{\dagger} \circ f=N$, and ![]() $f\in \mathrm {GO}(\mathbb {Q})$ is regular. Then for every open relatively compact subset with zero measure boundary
$f\in \mathrm {GO}(\mathbb {Q})$ is regular. Then for every open relatively compact subset with zero measure boundary ![]() $\Omega \subset \mathcal {F}_{2d}$, we have
$\Omega \subset \mathcal {F}_{2d}$, we have
 \[ |\{(X,\ell_{2d},f)\in CM(N), (X,\ell_{2d})\in \Omega\}|\underset{N\rightarrow \infty}{\sim}\frac{\chi(\widehat{\mathcal{D}})\cdot\deg(V_N)}{\operatorname{Vol}(\widehat{\mathcal{D}})}\int_{\Omega}\omega_{\mathcal{D}}. \]
\[ |\{(X,\ell_{2d},f)\in CM(N), (X,\ell_{2d})\in \Omega\}|\underset{N\rightarrow \infty}{\sim}\frac{\chi(\widehat{\mathcal{D}})\cdot\deg(V_N)}{\operatorname{Vol}(\widehat{\mathcal{D}})}\int_{\Omega}\omega_{\mathcal{D}}. \]
6.3 Equidistribution of Hecke translates of the Torelli locus
We prove in this section Theorem 1.22 and Corollary 1.23. As the reader will notice, this is a statement about the dynamics of Hecke operators rather than the varieties themselves.
Let ![]() $S$ and
$S$ and ![]() $D$ be two subvarieties of
$D$ be two subvarieties of ![]() $\mathcal {A}_g$ of complimentary dimensions and let
$\mathcal {A}_g$ of complimentary dimensions and let ![]() $d$ be the dimension of
$d$ be the dimension of ![]() $S$. Let
$S$. Let ![]() $\omega _{G/H}$ be the pull–push form on
$\omega _{G/H}$ be the pull–push form on ![]() $\mathcal {A}_g\times \mathcal {A}_g$ as constructed in Theorem 5.22 with respect to the groups
$\mathcal {A}_g\times \mathcal {A}_g$ as constructed in Theorem 5.22 with respect to the groups ![]() $G=\mathrm {PGSp}_{2g}\times \mathrm {PGSp}_{2g}$ and
$G=\mathrm {PGSp}_{2g}\times \mathrm {PGSp}_{2g}$ and ![]() $H=\mathrm {PGSp}_{2g}$ embedded diagonally. We have an inclusion
$H=\mathrm {PGSp}_{2g}$ embedded diagonally. We have an inclusion ![]() $\iota :S\times D\hookrightarrow \mathcal {A}_{g}\times \mathcal {A}_{g}$.
$\iota :S\times D\hookrightarrow \mathcal {A}_{g}\times \mathcal {A}_{g}$.
Let, as before, ![]() $\mathcal {F}^{1}\rightarrow \mathcal {A}_g$ be the Hodge bundle of the universal abelian scheme
$\mathcal {F}^{1}\rightarrow \mathcal {A}_g$ be the Hodge bundle of the universal abelian scheme ![]() $\mathcal {A}_g$ and let
$\mathcal {A}_g$ and let ![]() $\omega$ be its first Chern form with respect to the Hodge metric. Finally, let
$\omega$ be its first Chern form with respect to the Hodge metric. Finally, let ![]() $\omega _{S}$ and
$\omega _{S}$ and ![]() $\omega _{D}$ be its restriction to
$\omega _{D}$ be its restriction to ![]() $S$ and
$S$ and ![]() $D$, respectively.
$D$, respectively.
Lemma 6.20 We have ![]() $\iota ^{*}\omega _{G/H}=({1}/{{\rm Vol}(\widehat{\mathbb{H}}_g)}) \omega _{S}^d\wedge \omega _{D}^{{g(g+1)}/{2}-d}$.
$\iota ^{*}\omega _{G/H}=({1}/{{\rm Vol}(\widehat{\mathbb{H}}_g)}) \omega _{S}^d\wedge \omega _{D}^{{g(g+1)}/{2}-d}$.
Proof. This is a consequence of Theorem 5.22 as the only non-vanishing differential forms are the product of a form of degree ![]() $2d$ and a form of degree
$2d$ and a form of degree ![]() $g(g+1)-2d$, as the others vanish on
$g(g+1)-2d$, as the others vanish on ![]() $S\times D$, combined with the fact that
$S\times D$, combined with the fact that ![]() $H^{2d}(\mathcal {A}_g,\mathbb {R})$ is generated by
$H^{2d}(\mathcal {A}_g,\mathbb {R})$ is generated by ![]() $\omega ^d$ for
$\omega ^d$ for ![]() $d\leq 2$, see [Reference van der GeervdG99, Proposition 2.2], and whose dual form (in the sense preceding Theorem 5.22) is simply
$d\leq 2$, see [Reference van der GeervdG99, Proposition 2.2], and whose dual form (in the sense preceding Theorem 5.22) is simply ![]() $({1}/{{\rm Vol}(\widehat {\mathbb {H}}_g)})\omega ^{g(g+1)/2-d}$ because the volume form on
$({1}/{{\rm Vol}(\widehat {\mathbb {H}}_g)})\omega ^{g(g+1)/2-d}$ because the volume form on ![]() $\mathcal {A}_g$ is
$\mathcal {A}_g$ is ![]() $\omega ^{g(g+1)/2}$, hence the result.
$\omega ^{g(g+1)/2}$, hence the result.
It is well-known that ![]() $\omega$ is Kähler form on
$\omega$ is Kähler form on ![]() $\mathcal {A}_g$ and, hence, the integration of
$\mathcal {A}_g$ and, hence, the integration of ![]() $\omega _{S}^d$ and
$\omega _{S}^d$ and ![]() $\omega _{D}^{{g(g+1)}/{2}-1}$ define Lebesgue measures on
$\omega _{D}^{{g(g+1)}/{2}-1}$ define Lebesgue measures on ![]() $S$ and
$S$ and ![]() $D$, respectively, which are in fact finite by [Reference MumfordMum77, Main Theorem 3.1]. Finally, for
$D$, respectively, which are in fact finite by [Reference MumfordMum77, Main Theorem 3.1]. Finally, for ![]() $(s,d)\in S\times D$, an isogeny
$(s,d)\in S\times D$, an isogeny ![]() $f:\mathcal {A}_{S,s}\rightarrow \mathcal {A}_{D,d}$ is said to be regular if it does not admit first-order deformation or, equivalently,
$f:\mathcal {A}_{S,s}\rightarrow \mathcal {A}_{D,d}$ is said to be regular if it does not admit first-order deformation or, equivalently, ![]() $S\times D$ intersects
$S\times D$ intersects ![]() $\mathcal {C}_f$ transversely at
$\mathcal {C}_f$ transversely at ![]() $(s,d)$.
$(s,d)$.
Theorem 6.21 For every open relatively compact subsets with zero measure boundary ![]() $\Omega \subset S$ and
$\Omega \subset S$ and ![]() $\Omega '\subset D$, we have
$\Omega '\subset D$, we have
 \begin{align*}
|\{(s,d,f)&\mid (s,d)\in
\Omega\times \Omega', f\in
\mathrm{Isog}^N(\mathcal{A}_{S,s},
\mathcal{A}_{D,d}),f\,\text{is regular}\}|\\
&\underset{N\rightarrow \infty}{\sim}\deg(V_N)\cdot
\frac{\chi(\widehat{\mathbb{H}}_g)}{\operatorname{Vol}(\widehat{\mathbb{H}}_g)}\int_\Omega\omega_{S}^d\int_{\Omega'}\omega_D^{{g(g+1)}/{2}-d}.
\end{align*}
\begin{align*}
|\{(s,d,f)&\mid (s,d)\in
\Omega\times \Omega', f\in
\mathrm{Isog}^N(\mathcal{A}_{S,s},
\mathcal{A}_{D,d}),f\,\text{is regular}\}|\\
&\underset{N\rightarrow \infty}{\sim}\deg(V_N)\cdot
\frac{\chi(\widehat{\mathbb{H}}_g)}{\operatorname{Vol}(\widehat{\mathbb{H}}_g)}\int_\Omega\omega_{S}^d\int_{\Omega'}\omega_D^{{g(g+1)}/{2}-d}.
\end{align*}
In particular, the locus of points in ![]() $S$ isogenous to a point in
$S$ isogenous to a point in ![]() $D$ is analytically dense in
$D$ is analytically dense in ![]() $S$.
$S$.
Proof of Theorem 1.22 For every ![]() $N\geq 1$, we have defined the Hecke correspondence
$N\geq 1$, we have defined the Hecke correspondence ![]() $\mathcal {C}_N\hookrightarrow \mathcal {A}_g\times \mathcal {A}_g$ which parameterizes pairs of principally polarized abelian varieties together with a polarized isogeny with similitude factor equal to
$\mathcal {C}_N\hookrightarrow \mathcal {A}_g\times \mathcal {A}_g$ which parameterizes pairs of principally polarized abelian varieties together with a polarized isogeny with similitude factor equal to ![]() $N$. By the previous lemma, the restriction of the pull–push form
$N$. By the previous lemma, the restriction of the pull–push form ![]() $\omega _{G/H}$ is Kähler, hence the generic transversality assumption in Proposition 5.9 is satisfied and we are in the setting of Theorem 1.1: the transverse intersection locus of
$\omega _{G/H}$ is Kähler, hence the generic transversality assumption in Proposition 5.9 is satisfied and we are in the setting of Theorem 1.1: the transverse intersection locus of ![]() $S\times D$ and
$S\times D$ and ![]() $\mathcal {C}_N$ is equidistributed with respect to
$\mathcal {C}_N$ is equidistributed with respect to ![]() $({\chi (\widehat {\mathbb {H}}_g)}/{\operatorname {Vol}(\widehat {\mathbb {H}}_g)})\omega _{S}^d\wedge \omega ^{g(g+1)/2-d}_{D}$ as
$({\chi (\widehat {\mathbb {H}}_g)}/{\operatorname {Vol}(\widehat {\mathbb {H}}_g)})\omega _{S}^d\wedge \omega ^{g(g+1)/2-d}_{D}$ as ![]() $N\rightarrow \infty$. By the discussion preceding the theorem, the transverse locus is exactly given by regular isogenies. Hence, by choosing subsets of the form
$N\rightarrow \infty$. By the discussion preceding the theorem, the transverse locus is exactly given by regular isogenies. Hence, by choosing subsets of the form ![]() $\Omega \times \Omega '$, we obtain the desired equidistribution result. One has also similar equidistribution results on
$\Omega \times \Omega '$, we obtain the desired equidistribution result. One has also similar equidistribution results on ![]() $D$.
$D$.
Let ![]() $g\geq 2$ and let
$g\geq 2$ and let ![]() $\mathscr {M}_g$ be the coarse moduli space parameterizing smooth projective genus
$\mathscr {M}_g$ be the coarse moduli space parameterizing smooth projective genus ![]() $g$ curves over
$g$ curves over ![]() $\mathbb {C}$. Recall that for any such curve
$\mathbb {C}$. Recall that for any such curve ![]() $C$, one can associate its Jacobian
$C$, one can associate its Jacobian ![]() $J(C)$, which is a principally polarized abelian variety of dimension
$J(C)$, which is a principally polarized abelian variety of dimension ![]() $g$ over
$g$ over ![]() $\mathbb {C}$. This construction can be done in families so that we get a map, the Torelli map,
$\mathbb {C}$. This construction can be done in families so that we get a map, the Torelli map, ![]() $\iota _g:\mathscr {M}_g\hookrightarrow \mathcal {A}_g$ between coarse moduli spaces. This map is injective by [Reference Oort and SteenbrinkOS80] and its image is called the Torelli locus. For
$\iota _g:\mathscr {M}_g\hookrightarrow \mathcal {A}_g$ between coarse moduli spaces. This map is injective by [Reference Oort and SteenbrinkOS80] and its image is called the Torelli locus. For ![]() $g=4$, the Torelli locus is a divisor in
$g=4$, the Torelli locus is a divisor in ![]() $\mathcal {A}_4$. Hence, Corollary 1.23 follows by applying the previous theorem to
$\mathcal {A}_4$. Hence, Corollary 1.23 follows by applying the previous theorem to ![]() $D=\mathscr {M}_4$.
$D=\mathscr {M}_4$.
Acknowledgements
We thank B. Klingler for suggesting the use of o-minimality and Gabriele Mondello for pointing out the Giambelli–Porteous–Thom formula. The application to Hecke translates of the Torelli locus was raised during a fruitful discussion with Ananth Shankar and Yunqing Tang, to whom we are grateful. We also thank O. Benoist, N. Bergeron, F. Charles, P. Griffiths, and S.-W. Zhang for many useful discussions. S.T. also thanks CRM in Montréal and IAS in Princeton for excellent working conditions. We also thank the referees for their careful reading of the paper and useful comments.