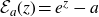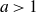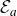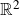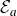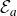1. Introduction
Let
![]() $f\,{:}\, {\mathbb{R}}^n \to {\mathbb{R}}^n$
be a function, and let
$f\,{:}\, {\mathbb{R}}^n \to {\mathbb{R}}^n$
be a function, and let
![]() $f^n$
denote the nth iterate of f. In this paper we are interested in the iteration of a continuous function
$f^n$
denote the nth iterate of f. In this paper we are interested in the iteration of a continuous function
![]() $f\,{:}\,{\mathbb{R}}^2 \to {\mathbb{R}}^2$
, which need not be analytic, and throughout we identify
$f\,{:}\,{\mathbb{R}}^2 \to {\mathbb{R}}^2$
, which need not be analytic, and throughout we identify
![]() ${\mathbb{R}}^2$
with the complex plane
${\mathbb{R}}^2$
with the complex plane
![]() ${\mathbb{C}}$
in the obvious way. A special case of such a function is when
${\mathbb{C}}$
in the obvious way. A special case of such a function is when
![]() $f\,{:}\,{\mathbb{C}} \to {\mathbb{C}}$
is transcendental entire. Then we define the Julia set J(f) as the set of points
$f\,{:}\,{\mathbb{C}} \to {\mathbb{C}}$
is transcendental entire. Then we define the Julia set J(f) as the set of points
![]() $z \in {\mathbb{C}}$
where the iterates
$z \in {\mathbb{C}}$
where the iterates
![]() $\{f^n\}_{n \in \mathbb{N}}$
fail to form a normal family in any neighbourhood of z; roughly speaking, the iterates of f are chaotic near a point in the Julia set. For an introduction to the properties of the Julia set, and the dynamics of transcendental entire functions, see, for example, [Reference Bergweiler3,Reference Schleicher16].
$\{f^n\}_{n \in \mathbb{N}}$
fail to form a normal family in any neighbourhood of z; roughly speaking, the iterates of f are chaotic near a point in the Julia set. For an introduction to the properties of the Julia set, and the dynamics of transcendental entire functions, see, for example, [Reference Bergweiler3,Reference Schleicher16].
In the study of the dynamics of transcendental entire functions, many authors have considered maps of the form
It is straightforward to show that
![]() $\mathcal{E}_a$
has an attracting fixed point
$\mathcal{E}_a$
has an attracting fixed point
![]() $\xi \in {\mathbb{R}}$
. We denote by F the set of points that are attracted to
$\xi \in {\mathbb{R}}$
. We denote by F the set of points that are attracted to
![]() $\xi$
; in other words
$\xi$
; in other words
It can be shown that
![]() $J(\mathcal{E}_a) = {\mathbb{C}} \setminus F$
. (Clearly F here is the Fatou set of
$J(\mathcal{E}_a) = {\mathbb{C}} \setminus F$
. (Clearly F here is the Fatou set of
![]() $\mathcal{E}_a$
, but we do not use this fact.)
$\mathcal{E}_a$
, but we do not use this fact.)
The first study of the dynamics of maps of the form (1) was by Devaney and Krych [Reference Devaney and Krych7]. Many authors since then have investigated these maps, and in the following we summarise some of the most important results that are known concerning their dynamical properties. Before stating the result we need a number of definitions.
We say that a component
![]() $\gamma$
of
$\gamma$
of
![]() $J(\mathcal{E}_a)$
is a Devaney hair if it is a simple curve
$J(\mathcal{E}_a)$
is a Devaney hair if it is a simple curve
![]() $\gamma \,{:}\, [0, \infty) \to {\mathbb{C}}$
with the properties that:
$\gamma \,{:}\, [0, \infty) \to {\mathbb{C}}$
with the properties that:
-
(i)
 $\gamma(t) \rightarrow \infty$
as
$\gamma(t) \rightarrow \infty$
as
 $t \rightarrow \infty$
.
$t \rightarrow \infty$
. -
(ii) for each
 $n \geq 0$
,
$n \geq 0$
,
 $\mathcal{E}_a^n(\gamma)$
is a simple curve that connects
$\mathcal{E}_a^n(\gamma)$
is a simple curve that connects
 $\mathcal{E}_a^n(\gamma(0))$
to
$\mathcal{E}_a^n(\gamma(0))$
to
 $\infty$
. We call
$\infty$
. We call
 $\gamma(0)$
the endpoint of the curve
$\gamma(0)$
the endpoint of the curve
 $\gamma$
.
$\gamma$
. -
(iii) for each
 $t>0$
,
$t>0$
,
 $\mathcal{E}_a^n \rightarrow\infty$
as
$\mathcal{E}_a^n \rightarrow\infty$
as
 $n\rightarrow\infty$
uniformly on
$n\rightarrow\infty$
uniformly on
 $\gamma([t,\infty))$
.
$\gamma([t,\infty))$
.
Note that there are other definitions of a Devaney hair in the literature; we have used the definition first used in [Reference Lasse Rempe14], although, unlike in that paper, we do not formally specify that the hairs lie in the Julia set.
A subset of
![]() ${\mathbb{C}}$
is a Cantor bouquet if it is ambiently homeomorphic to a topological object known as a straight brush; see [Reference Aarts and Oversteegen1] for a precise definition. We say that
${\mathbb{C}}$
is a Cantor bouquet if it is ambiently homeomorphic to a topological object known as a straight brush; see [Reference Aarts and Oversteegen1] for a precise definition. We say that
![]() $X \subset \hat{\mathbb{C}}$
is totally separated if for all
$X \subset \hat{\mathbb{C}}$
is totally separated if for all
![]() $a, b \in X$
, with
$a, b \in X$
, with
![]() $a\neq b$
, there exists a relatively open and closed set
$a\neq b$
, there exists a relatively open and closed set
![]() $U \subset X$
such that
$U \subset X$
such that
![]() $a \in U$
and
$a \in U$
and
![]() $b \notin U$
.
$b \notin U$
.
We are now able to state the results.
Theorem A. Let
![]() $\mathcal{E}_a$
be the transcendental entire function defined in (1). Then the following all hold.
$\mathcal{E}_a$
be the transcendental entire function defined in (1). Then the following all hold.
-
(a)
 $J(\mathcal{E}_a)$
has uncountably many components, each of which is a Devaney hair.
$J(\mathcal{E}_a)$
has uncountably many components, each of which is a Devaney hair. -
(b)
 $J(\mathcal{E}_a)$
is a Cantor bouquet.
$J(\mathcal{E}_a)$
is a Cantor bouquet. -
(c) Write E for the set of endpoints of the Devaney hairs in
 $J(\mathcal{E}_a)$
. Then E is totally separated, but
$J(\mathcal{E}_a)$
. Then E is totally separated, but
 $E \cup \{\infty\}$
is connected.
$E \cup \{\infty\}$
is connected.
Remarks. Part (a) seems to be a combination of results from [Reference Devaney and Tangerman8,Reference Karpińska9,Reference Rempe12]. Part (b) is a result of [Reference Aarts and Oversteegen1]; although the term “Cantor bouquet” had been used previously, this was the first paper to give a precise topological definition of such an object. Part (c) is from [Reference Mayer10]; this result can also be stated that
![]() $\infty$
is an explosion point for the set
$\infty$
is an explosion point for the set
![]() $E \cup \{\infty\}$
. Note that many of the authors cited above considered, in fact, the transcendental entire functions
$E \cup \{\infty\}$
. Note that many of the authors cited above considered, in fact, the transcendental entire functions
![]() $\tilde{\mathcal{E}}_\lambda(z) \,{:\!=}\, \lambda e^z$
, for
$\tilde{\mathcal{E}}_\lambda(z) \,{:\!=}\, \lambda e^z$
, for
![]() $\lambda \ne 0$
. The functions
$\lambda \ne 0$
. The functions
![]() $\mathcal{E}_a$
and
$\mathcal{E}_a$
and
![]() $\tilde{\mathcal{E}}_{e^{-a}}$
have the same dynamics, as they are conjugate via the map
$\tilde{\mathcal{E}}_{e^{-a}}$
have the same dynamics, as they are conjugate via the map
![]() $z \mapsto z - a$
.
$z \mapsto z - a$
.
Our aim in this paper is to show that there is a large class of continuous functions
![]() $f \,{:}\, {\mathbb{R}}^2 \to {\mathbb{R}}^2$
that are analogous to the map
$f \,{:}\, {\mathbb{R}}^2 \to {\mathbb{R}}^2$
that are analogous to the map
![]() $\mathcal{E}_a$
and also have the dynamical properties listed above. This shows that, in some sense, the properties listed in Theorem A derive from elementary function theoretic properties of
$\mathcal{E}_a$
and also have the dynamical properties listed above. This shows that, in some sense, the properties listed in Theorem A derive from elementary function theoretic properties of
![]() $\mathcal{E}_a$
rather than its analyticity. We stress that the functions in our class are continuous but not necessarily quasiregular.
$\mathcal{E}_a$
rather than its analyticity. We stress that the functions in our class are continuous but not necessarily quasiregular.
To define our maps, we observe that if
![]() $z = x + iy$
, then
$z = x + iy$
, then
![]() $e^z = e^x(\cos y + i \sin y)$
. So we begin by considering a map
$e^z = e^x(\cos y + i \sin y)$
. So we begin by considering a map
where
![]() $g \,{:}\, {\mathbb{R}} \to {\mathbb{R}}$
and
$g \,{:}\, {\mathbb{R}} \to {\mathbb{R}}$
and
![]() $h \,{:}\, {\mathbb{R}} \to {\mathbb{C}}$
are continuous functions defined in such a way that g has behaviour analogous to the real exponential function, and h has behaviour analogous to the map
$h \,{:}\, {\mathbb{R}} \to {\mathbb{C}}$
are continuous functions defined in such a way that g has behaviour analogous to the real exponential function, and h has behaviour analogous to the map
![]() $y \mapsto \cos y + i \sin y$
.
$y \mapsto \cos y + i \sin y$
.
We first specify the map h. We suppose that
![]() $h \,{:}\, {\mathbb{R}} \to {\mathbb{C}}$
is a
$h \,{:}\, {\mathbb{R}} \to {\mathbb{C}}$
is a
![]() $2\pi$
-periodic function such that
$2\pi$
-periodic function such that
![]() $h \,{:}\, [0, 2\pi) \to {\mathbb{C}}$
is biLipschitz, such that
$h \,{:}\, [0, 2\pi) \to {\mathbb{C}}$
is biLipschitz, such that
![]() $\arg h(y)$
is a strictly monotonic increasing function of y, and such that the origin lies in the bounded complementary component of
$\arg h(y)$
is a strictly monotonic increasing function of y, and such that the origin lies in the bounded complementary component of
![]() $h([0, 2\pi))$
.
$h([0, 2\pi))$
.
It is also useful to set
![]() $h(y) \,{:\!=}\, h_1(y) + i h_2(y)$
, for real valued functions
$h(y) \,{:\!=}\, h_1(y) + i h_2(y)$
, for real valued functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
. Note also that it follows from the above that there exists
$h_2$
. Note also that it follows from the above that there exists
![]() $h_{\alpha} \in (0,1)$
and
$h_{\alpha} \in (0,1)$
and
![]() $h_{\beta} \in (1, \infty)$
such that
$h_{\beta} \in (1, \infty)$
such that
Next we specify the function g. We let
![]() $g \,{:}\, {\mathbb{R}} \to (0, \infty)$
be a convex function such that
$g \,{:}\, {\mathbb{R}} \to (0, \infty)$
be a convex function such that
![]() $g(x) \to 0$
as
$g(x) \to 0$
as
![]() $x\to -\infty$
. In addition, to ensure that g grows sufficiently quickly, we suppose that there exists
$x\to -\infty$
. In addition, to ensure that g grows sufficiently quickly, we suppose that there exists
![]() $c > h_{\beta}/h_{\alpha} > 1$
such that,
$c > h_{\beta}/h_{\alpha} > 1$
such that,
Note that, since
![]() $c>1$
, we must have that
$c>1$
, we must have that
![]() $g'(x) \rightarrow \infty$
, as
$g'(x) \rightarrow \infty$
, as
![]() $x \rightarrow \infty$
, where defined. In addition, it is easy to deduce from (3), together with the convexity of g, that there is a constant
$x \rightarrow \infty$
, where defined. In addition, it is easy to deduce from (3), together with the convexity of g, that there is a constant
![]() $x_0 > 0$
such that
$x_0 > 0$
such that
We then define the map Z mentioned earlier by
Note that it follows from the definition of h that Z can also be written in the form
where k(y) and m(y) are real, positive, Lipschitz and bi-Lipschitz functions respectively. However we do not use this fact. Note that when
![]() $g(x) = e^x$
, the function Z in (5) is quasiregular, and is known as a Zorich map. If, in addition,
$g(x) = e^x$
, the function Z in (5) is quasiregular, and is known as a Zorich map. If, in addition,
![]() $h(y) = \cos y + i \sin y$
, then we have
$h(y) = \cos y + i \sin y$
, then we have
![]() $Z \equiv \exp$
.
$Z \equiv \exp$
.
Finally we define the function we are going to iterate. We let
![]() $a > 0$
and set
$a > 0$
and set
We will later ensure that a is sufficiently large for various conditions to hold. We then make the following definition.
Definition 1·1. Suppose that f is as defined in (6), where Z is as defined in (5) for functions g, h that satisfy all the conditions listed earlier. Then we say that f is a generalised exponential.
Although not necessarily quasiregular, f is continuous, open, discrete, and, by Rademacher’s theorem, differentiable almost everywhere. Note also that it follows from these definitions that any local inverse of f is also continuous and differentiable almost everywhere. The name for the generalised exponentials can be further justified by the fact that no polynomial can satisfy condition (3).
For a generalised exponential, f, there is no obvious definition of a Julia set; although the Julia set can be defined for quasiregular maps [Reference Bergweiler and Nicks6], we do not want to assume that f is even quasiregular. The following result allows us, nonetheless, to establish a set analogous to the Julia set. Here we define
Theorem 1·2. Suppose that f is a generalised exponential. Then, there exist
![]() $m<0$
and
$m<0$
and
![]() $M>0$
such that whenever a is sufficiently large, f has a unique attracting fixed point
$M>0$
such that whenever a is sufficiently large, f has a unique attracting fixed point
![]() $\xi \in \mathbb{H}_m$
,
$\xi \in \mathbb{H}_m$
,
![]() $f(\mathbb{H}_M) \subset \mathbb{H}_m$
, and all points of
$f(\mathbb{H}_M) \subset \mathbb{H}_m$
, and all points of
![]() $\mathbb{H}_M$
tend to
$\mathbb{H}_M$
tend to
![]() $\xi$
under iteration.
$\xi$
under iteration.
We can now use Theorem 1·2 to make the following natural definition.
Definition 1·3 If the conditions of Theorem 1·2 hold, then we let F denote the set of points that iterate to the unique attracting fixed point, and set
![]() $J \,{:\!=}\, {\mathbb{C}} \setminus F$
.
$J \,{:\!=}\, {\mathbb{C}} \setminus F$
.
Our main result is then an extension of Theorem A to the class of generalised exponentials.
Theorem 1·4. Suppose that f is a generalised exponential. Then, for all sufficiently large values of a, the following all hold.
-
(a) J has uncountably many components, each of which is a Devaney hair.
-
(b) J is a Cantor bouquet.
-
(c) If E is the set of endpoints of the Devaney hairs in J, then E is totally separated, but
 $E \cup \{\infty\}$
is connected.
$E \cup \{\infty\}$
is connected.
Note that the fact that J has uncountably many components is also a consequence of (b). However, it seems worth emphasising this fact.
Structure The structure of the paper is as follows. First in Section 2 we prove Theorem 1·2. The proof of Theorem 1·4 is then spread across the rest of the paper.
2. Existence of the sets F and J
In this section we give the proof of Theorem 1·2, and so establish the existence of the sets F and J from Definition 1·3. Firstly, we need a form of expansion for Z, which is given in the following lemma. Here, for
![]() $f \,{:}\, {\mathbb{C}} \to {\mathbb{C}}$
differentiable a.e., we define
$f \,{:}\, {\mathbb{C}} \to {\mathbb{C}}$
differentiable a.e., we define
Lemma 2·1. There exist constants
![]() $\mu > 1$
and
$\mu > 1$
and
![]() $M > 0$
such that
$M > 0$
such that
Proof. For the derivative of Z we have, whenever it exists, that
 \begin{equation*}DZ(x+iy) \,{:\!=}\, A \,{:\!=}\, \left(\begin{array}{c@{\quad}c}g'(x) h_1(y) & g(x) h_1^{\prime}(y) \\ \\[-7pt] g'(x) h_2(y) & g(x) h_2^{\prime}(y)\end{array}\right)= \left(\begin{array}{c@{\quad}c}h_1(y) & h_1^{\prime}(y) \\ \\[-7pt] h_2(y) & h_2^{\prime}(y)\end{array}\right) \cdot\left(\begin{array}{c@{\quad}c}g'(x) & 0 \\ \\[-7pt] 0 & g(x)\end{array}\right).\end{equation*}
\begin{equation*}DZ(x+iy) \,{:\!=}\, A \,{:\!=}\, \left(\begin{array}{c@{\quad}c}g'(x) h_1(y) & g(x) h_1^{\prime}(y) \\ \\[-7pt] g'(x) h_2(y) & g(x) h_2^{\prime}(y)\end{array}\right)= \left(\begin{array}{c@{\quad}c}h_1(y) & h_1^{\prime}(y) \\ \\[-7pt] h_2(y) & h_2^{\prime}(y)\end{array}\right) \cdot\left(\begin{array}{c@{\quad}c}g'(x) & 0 \\ \\[-7pt] 0 & g(x)\end{array}\right).\end{equation*}
The fact that h is biLipschitz yields, again by Rademacher’s theorem, that h
![]() $^{\prime}$
exists almost everywhere.
$^{\prime}$
exists almost everywhere.
It is well known that
It follows by the definition of A and [Reference Bergweiler4, section 2] that for a suitable constant
![]() $c_h >0$
, which depends only on the Lipschitz constant of h
$c_h >0$
, which depends only on the Lipschitz constant of h
Since
![]() $|h(y)| \geq h_{\alpha} > 0$
, and since both g
$|h(y)| \geq h_{\alpha} > 0$
, and since both g
![]() $^{\prime}$
(x) (where defined) and g(x) tend to infinity as x tends to infinity, the result then follows by a simple exercise, which we omit.
$^{\prime}$
(x) (where defined) and g(x) tend to infinity as x tends to infinity, the result then follows by a simple exercise, which we omit.
Proof of Theorem 1·2. Let
![]() $M>0$
be the constant from Lemma 2·1. Since h is biLipschitz, there exists a constant
$M>0$
be the constant from Lemma 2·1. Since h is biLipschitz, there exists a constant
![]() $L\geq 1$
such that
$L\geq 1$
such that
Since g(x) and g
![]() $^{\prime}$
(x) (where defined) both tend to 0 as x tends to
$^{\prime}$
(x) (where defined) both tend to 0 as x tends to
![]() $-\infty$
, we can choose
$-\infty$
, we can choose
![]() $m<0$
sufficiently small that
$m<0$
sufficiently small that
We deduce that
 \begin{align*}|DZ(x+iy)| &\leq |g'(x) h_1(y)| + |g(x) h_1^{\prime}(y)| + |g'(x) h_2(y)| + |g(x) h_2^{\prime}(y)| \\[3pt] &\leq (L+1)(g'(x)+g(x)) \\[3pt] &\leq \frac{1}{2}, \quad\text{a.e. for } x \leq m.\end{align*}
\begin{align*}|DZ(x+iy)| &\leq |g'(x) h_1(y)| + |g(x) h_1^{\prime}(y)| + |g'(x) h_2(y)| + |g(x) h_2^{\prime}(y)| \\[3pt] &\leq (L+1)(g'(x)+g(x)) \\[3pt] &\leq \frac{1}{2}, \quad\text{a.e. for } x \leq m.\end{align*}
Since
![]() $DZ(x+iy)=Df(x,y)$
it follows that
$DZ(x+iy)=Df(x,y)$
it follows that
Now choose
(Note that the choice of a here is stronger than is required in this proof, but convenient for use in later results).
If
![]() $x \leq M$
, then
$x \leq M$
, then
In other words,
![]() $f(\mathbb{H}_M) \subset \mathbb{H}_m$
. Hence f is a contraction mapping on
$f(\mathbb{H}_M) \subset \mathbb{H}_m$
. Hence f is a contraction mapping on
![]() $\mathbb{H}_m$
, and so
$\mathbb{H}_m$
, and so
![]() $\mathbb{H}_m$
contains a unique attracting fixed point
$\mathbb{H}_m$
contains a unique attracting fixed point
![]() $\xi$
by the Banach fixed point theorem. Since f is expanding in the complement of
$\xi$
by the Banach fixed point theorem. Since f is expanding in the complement of
![]() $\mathbb{H}_M$
, by Lemma 2·1, the uniqueness of
$\mathbb{H}_M$
, by Lemma 2·1, the uniqueness of
![]() $\xi$
is immediate.
$\xi$
is immediate.
In the remainder of the paper we will assume that f, g, h, Z are as defined above, that f is a generalised exponential, and that a has been chosen such that (8) holds.

Fig. 1. An illustration of J for the generalised exponential with
![]() $a=2$
, with
$a=2$
, with
![]() $g(x) = e^x$
, and with h being the obvious extension of the linear maps from
$g(x) = e^x$
, and with h being the obvious extension of the linear maps from
![]() $[0, \pi/2]$
to [1, i],
$[0, \pi/2]$
to [1, i],
![]() $[\pi/2, \pi]$
to
$[\pi/2, \pi]$
to
![]() $[i, -1]$
, and so on.
$[i, -1]$
, and so on.

Fig. 2. An illustration of J for the function with
![]() $a=1$
, with
$a=1$
, with
![]() $h(y) = (\cos y, \sin y)$
, and with
$h(y) = (\cos y, \sin y)$
, and with
![]() $g(x) = 0$
in the left half-plane and
$g(x) = 0$
in the left half-plane and
![]() $g(x) = x^3$
in the right half-plane. Note that this function is not covered by the results of this paper. However, it is still possible to define J in a similar way, and we still observe some of the features of J that we might expect.
$g(x) = x^3$
in the right half-plane. Note that this function is not covered by the results of this paper. However, it is still possible to define J in a similar way, and we still observe some of the features of J that we might expect.
3. Symbolic dynamics
In this section we define tracts and external addresses, and then use these to establish symbolic dynamics on J. We begin by defining the tracts of the function g. Since
![]() $-a < 0 < M$
, we have that
$-a < 0 < M$
, we have that
![]() $\mathbb{H}_{-a} \subset \mathbb{H}_M$
, and so points with imaginary part in an interval
$\mathbb{H}_{-a} \subset \mathbb{H}_M$
, and so points with imaginary part in an interval
![]() $[(4k+1)\pi/2, (4k+3)\pi/2]$
, for some
$[(4k+1)\pi/2, (4k+3)\pi/2]$
, for some
![]() $k \in {\mathbb{Z}}$
, necessarily lie in F.
$k \in {\mathbb{Z}}$
, necessarily lie in F.
Definition 3·1 Let
![]() $t_1 \in [0, 2\pi]$
be such that Re
$t_1 \in [0, 2\pi]$
be such that Re
![]() $h(t_1)=0$
, and Im
$h(t_1)=0$
, and Im
![]() $h(t_1) >0$
. Similarly let
$h(t_1) >0$
. Similarly let
![]() $t_2 \in [0, 2\pi]$
be such that Re
$t_2 \in [0, 2\pi]$
be such that Re
![]() $h(t_2)=0$
, and Im
$h(t_2)=0$
, and Im
![]() $h(t_1)<0$
. If
$h(t_1)<0$
. If
![]() $t_2 > t_1$
, then we replace
$t_2 > t_1$
, then we replace
![]() $t_2$
with
$t_2$
with
![]() $t_2 - 2\pi$
. (It is easy to see from the definition of h that these exist and are unique. For each
$t_2 - 2\pi$
. (It is easy to see from the definition of h that these exist and are unique. For each
![]() $k \in {\mathbb{Z}}$
, define the tract
$k \in {\mathbb{Z}}$
, define the tract
![]() $T_k$
by
$T_k$
by
Also set
Clearly H is the image of any tract. Geometrically H is the right half-plane with a bounded set removed; in particular
We stress that the sets
![]() $T_k$
are not tracts in the sense usually defined for functions in the class
$T_k$
are not tracts in the sense usually defined for functions in the class
![]() ${\mathcal{B}}$
. However, if
${\mathcal{B}}$
. However, if
![]() $T_k, T_{k'}$
are both tracts, then it follows by (8) that
$T_k, T_{k'}$
are both tracts, then it follows by (8) that
![]() $\overline{T_{k'}} \subset f(T_k) = H$
; abusing slightly the terminology of class
$\overline{T_{k'}} \subset f(T_k) = H$
; abusing slightly the terminology of class
![]() ${\mathcal{B}}$
maps, f is of disjoint type.
${\mathcal{B}}$
maps, f is of disjoint type.
Note also that if
![]() $T_k$
is a tract, then
$T_k$
is a tract, then
![]() $f \,{:}\, T_k \to H$
is a continuous bijection, and in fact the same is true for
$f \,{:}\, T_k \to H$
is a continuous bijection, and in fact the same is true for
![]() $f \,{:}\, \overline{T_k} \to \overline{H}$
. (This follows from the definitions of g and h; in fact f is a bijection on a set slightly larger than
$f \,{:}\, \overline{T_k} \to \overline{H}$
. (This follows from the definitions of g and h; in fact f is a bijection on a set slightly larger than
![]() $T_k$
.) Since
$T_k$
.) Since
![]() $\overline{T_k}$
is compact in
$\overline{T_k}$
is compact in
![]() $\widehat{{\mathbb{C}}}$
, and since
$\widehat{{\mathbb{C}}}$
, and since
![]() $\overline{H}$
is a Hausdorff space, it follows that
$\overline{H}$
is a Hausdorff space, it follows that
![]() $f \,{:}\, T_k \to H$
is a homeomorphism. We denote the inverse of this restriction by
$f \,{:}\, T_k \to H$
is a homeomorphism. We denote the inverse of this restriction by
![]() $f_k^{-1}$
.
$f_k^{-1}$
.
More generally, if
![]() $k_1 k_2 \cdots k_n$
is a finite sequence of integers, then we define
$k_1 k_2 \cdots k_n$
is a finite sequence of integers, then we define
![]() $f_{k_1 k_2 \cdots k_n}^{-n} \,{:\!=}\, f_{k_1}^{-1} \circ \cdots \circ f_{k_n}^{-1}$
.
$f_{k_1 k_2 \cdots k_n}^{-n} \,{:\!=}\, f_{k_1}^{-1} \circ \cdots \circ f_{k_n}^{-1}$
.
Next we consider the components of J and define the notion of external addresses.
Proposition 3·2 Every component of J is unbounded.
Proof. Note that if
![]() $Y \subset H$
is connected and unbounded, and
$Y \subset H$
is connected and unbounded, and
![]() $k \in {\mathbb{Z}}$
, then
$k \in {\mathbb{Z}}$
, then
![]() $f_{k}^{-1}(Y)$
is connected and unbounded; connectedness follows from continuity, and unboundedness is a consequence of the fact that f is a homeomorphism of the closure of each tract.
$f_{k}^{-1}(Y)$
is connected and unbounded; connectedness follows from continuity, and unboundedness is a consequence of the fact that f is a homeomorphism of the closure of each tract.
For each
![]() $n \in {\mathbb{N}}$
, consider the set
$n \in {\mathbb{N}}$
, consider the set
Then, considered as a subset of the Riemann sphere,
![]() $F_n$
is connected, by the above remark, and compact; in other words,
$F_n$
is connected, by the above remark, and compact; in other words,
![]() $F_n$
is a continuum. It follows that
$F_n$
is a continuum. It follows that
is a nested intersection of continua, and so is itself a continuum. The result then follows by the “Boundary bumping theorem”; see, for example, [Reference Nadler11, theorem 5·6].
We write
![]() $\mathbb{N}_0 = {\mathbb{N}} \cup \{0\}$
.
$\mathbb{N}_0 = {\mathbb{N}} \cup \{0\}$
.
Definition 3·3 Observe that
![]() $z \in J$
if and only if there is an external address
$z \in J$
if and only if there is an external address
![]() $\underline{s} = s_0 s_1 \cdots \in {\mathbb{Z}}^{\mathbb{N}_0}$
such that
$\underline{s} = s_0 s_1 \cdots \in {\mathbb{Z}}^{\mathbb{N}_0}$
such that
![]() $f^n(z) \in T_{s_n}$
, for
$f^n(z) \in T_{s_n}$
, for
![]() $n \geq 0$
. We write
$n \geq 0$
. We write
![]() $\underline{s} = \operatorname{addr}\!(z)$
. We also write
$\underline{s} = \operatorname{addr}\!(z)$
. We also write
![]() $J_{\underline{s}}$
for the set of points with external address
$J_{\underline{s}}$
for the set of points with external address
![]() $\underline{s}$
. Finally we let
$\underline{s}$
. Finally we let
![]() $\hat{J_{\underline{s}}}$
denote the closure of
$\hat{J_{\underline{s}}}$
denote the closure of
![]() $J_{\underline{s}}$
in
$J_{\underline{s}}$
in
![]() $\hat{{\mathbb{C}}}$
. If
$\hat{{\mathbb{C}}}$
. If
![]() $\underline{s}$
is an external address such that
$\underline{s}$
is an external address such that
![]() $J_{\underline{s}} \ne \emptyset$
, then we say that
$J_{\underline{s}} \ne \emptyset$
, then we say that
![]() $\underline{s}$
is admissible.
$\underline{s}$
is admissible.
The conclusions of the following observation are straightforward, and the proof is omitted. Here
![]() $\sigma$
is the Bernoulli shift map defined by
$\sigma$
is the Bernoulli shift map defined by
![]() $\sigma(s_0 s_1 s_2 \cdots) = s_1 s_2 \cdots$
.
$\sigma(s_0 s_1 s_2 \cdots) = s_1 s_2 \cdots$
.
Observation 3·4 Suppose that
![]() $\underline{s} = s_0 s_1 \cdots$
and
$\underline{s} = s_0 s_1 \cdots$
and
![]() $\underline{s}'$
are admissible external addresses, with
$\underline{s}'$
are admissible external addresses, with
![]() $\underline{s} \ne \underline{s}'$
. Then all the following hold:
$\underline{s} \ne \underline{s}'$
. Then all the following hold:
-
(i)
 $J_{\underline{s}} = \bigcap_{n \in {\mathbb{N}}} f_{s_0 s_1 \cdots s_{n-1}}^{-n}(H)$
$J_{\underline{s}} = \bigcap_{n \in {\mathbb{N}}} f_{s_0 s_1 \cdots s_{n-1}}^{-n}(H)$
-
(ii)
 $J_{\underline{s}}$
and
$J_{\underline{s}}$
and
 $J_{\underline{s}'}$
are disjoint
$J_{\underline{s}'}$
are disjoint -
(iii) if
 $n \in {\mathbb{N}}$
, then
$n \in {\mathbb{N}}$
, then
 $f^n(J_{\underline{s}}) = J_{\sigma^n(\underline{s})}$
.
$f^n(J_{\underline{s}}) = J_{\sigma^n(\underline{s})}$
.
Our next step is to characterise the admissible external addresses.
Definition 3·5 We say that an external address
![]() $\underline{s} \in {\mathbb{Z}}^{\mathbb{N}_0}$
is g-bounded if there exists
$\underline{s} \in {\mathbb{Z}}^{\mathbb{N}_0}$
is g-bounded if there exists
![]() $x_0^{\prime} \geq 0$
such that
$x_0^{\prime} \geq 0$
such that
Note that the constant
![]() $2\pi$
in (10) can, in fact, be replaced by any positive constant; indeed, this comment also applies to the choice of the constant
$2\pi$
in (10) can, in fact, be replaced by any positive constant; indeed, this comment also applies to the choice of the constant
![]() $2\pi$
in the definition of admissible external addresses in [Reference Devaney and Krych7]. We have used
$2\pi$
in the definition of admissible external addresses in [Reference Devaney and Krych7]. We have used
![]() $2\pi$
here for consistency.
$2\pi$
here for consistency.
We show that the admissible external addresses are identically the external addresses that are g-bounded, provided that g satisfies (4).
Theorem 3·6 Suppose that (4) holds, and that
![]() $\underline{s} \in {\mathbb{Z}}^{\mathbb{N}_0}$
. Then
$\underline{s} \in {\mathbb{Z}}^{\mathbb{N}_0}$
. Then
![]() $\underline{s}$
is admissible if and only if
$\underline{s}$
is admissible if and only if
![]() $\underline{s}$
is g-bounded.
$\underline{s}$
is g-bounded.
Proof. First, suppose that
![]() $\underline{s} = s_0 s_1 \cdots$
is admissible, and so there exists a point
$\underline{s} = s_0 s_1 \cdots$
is admissible, and so there exists a point
![]() $z = x + iy \in {\mathbb{C}}$
with external address
$z = x + iy \in {\mathbb{C}}$
with external address
![]() $\underline{s}$
. Note that
$\underline{s}$
. Note that
and indeed
Observe that it follows from (4) that there exists
![]() $x_0^{\prime} > 0$
such that
$x_0^{\prime} > 0$
such that
Hence, for
![]() $n \in \mathbb{N}_0$
,
$n \in \mathbb{N}_0$
,
and so
![]() $\underline{s}$
is indeed g-bounded.
$\underline{s}$
is indeed g-bounded.
In the other direction, suppose that
![]() $\underline{s} = s_0 s_1 \cdots \in {\mathbb{Z}}^{\mathbb{N}_0}$
is g-bounded. Recalling that
$\underline{s} = s_0 s_1 \cdots \in {\mathbb{Z}}^{\mathbb{N}_0}$
is g-bounded. Recalling that
![]() $c > h_{\beta}/h_{\alpha}$
, we can choose
$c > h_{\beta}/h_{\alpha}$
, we can choose
![]() $\kappa > 0$
small enough that
$\kappa > 0$
small enough that
 \[\kappa^2
< \frac{c^2h_{\alpha}^2}{h_{\beta}^2} - 1.\]
\[\kappa^2
< \frac{c^2h_{\alpha}^2}{h_{\beta}^2} - 1.\]
Let
![]() $\tilde{g}(x) \,{:\!=}\, h_{\beta} g(x)$
. It can be deduced from (4) and (10) that there exists
$\tilde{g}(x) \,{:\!=}\, h_{\beta} g(x)$
. It can be deduced from (4) and (10) that there exists
![]() $x_0^{\prime\prime} \geq 0$
such that
$x_0^{\prime\prime} \geq 0$
such that
Choose
![]() $\delta > 0$
sufficiently small that
$\delta > 0$
sufficiently small that
 \[(1+\delta)^2
< \frac{c^2h_{\alpha}^2}{h_{\beta}^2} - \kappa^2.\]
\[(1+\delta)^2
< \frac{c^2h_{\alpha}^2}{h_{\beta}^2} - \kappa^2.\]
We also choose
where
![]() $x_0$
is the constant from (4) and
$x_0$
is the constant from (4) and
![]() $M>0$
is the constant from Lemma 2·1.
$M>0$
is the constant from Lemma 2·1.
Increasing
![]() $r_0$
, if necessary, we can also assume that all points of real part at least
$r_0$
, if necessary, we can also assume that all points of real part at least
![]() $r_0$
lie in H. We then set
$r_0$
lie in H. We then set
![]() $r_{k+1} = \tilde{g}(r_k)$
, for
$r_{k+1} = \tilde{g}(r_k)$
, for
![]() $k \in \mathbb{N}_0$
.
$k \in \mathbb{N}_0$
.
For each
![]() $n \in \mathbb{N}_0$
, let
$n \in \mathbb{N}_0$
, let
![]() $D_n$
be the closed square of side
$D_n$
be the closed square of side
![]() $2\pi$
, with sides parallel to the axes, and with bottom left vertex at the point
$2\pi$
, with sides parallel to the axes, and with bottom left vertex at the point
![]() $r_n + 2\pi 4s_n$
.
$r_n + 2\pi 4s_n$
.
We claim that
![]() $f(D_n) \supset D_{n+1}$
, for
$f(D_n) \supset D_{n+1}$
, for
![]() $n \in \mathbb{N}_0$
. To prove the claim, first fix
$n \in \mathbb{N}_0$
. To prove the claim, first fix
![]() $n \in \mathbb{N}_0$
. Observe that the image under Z of the left-hand side of
$n \in \mathbb{N}_0$
. Observe that the image under Z of the left-hand side of
![]() $D_n$
contains points of modulus at most
$D_n$
contains points of modulus at most
![]() $h_{\beta} g(r_n)$
. Similarly, by (4), the image under Z of the right-hand side of
$h_{\beta} g(r_n)$
. Similarly, by (4), the image under Z of the right-hand side of
![]() $D_n$
contains points of modulus at least
$D_n$
contains points of modulus at least
![]() $h_{\alpha} c g(r_n)$
. We can deduce that
$h_{\alpha} c g(r_n)$
. We can deduce that
![]() $f(D_n)$
contains the annulus
$f(D_n)$
contains the annulus
Since
![]() $h_{\beta} g(r_n) = r_{n+1}$
, we can see that
$h_{\beta} g(r_n) = r_{n+1}$
, we can see that
![]() $D_{n+1}$
does not lie inside the inner radius of
$D_{n+1}$
does not lie inside the inner radius of
![]() $A_n$
. Hence it remains to prove that
$A_n$
. Hence it remains to prove that
![]() $D_{n+1}$
does not lie outside the outer radius of this annulus. Without loss of generality we can assume that
$D_{n+1}$
does not lie outside the outer radius of this annulus. Without loss of generality we can assume that
![]() $s_{n+1}$
is non-negative. A furthermost point of
$s_{n+1}$
is non-negative. A furthermost point of
![]() $D_{n+1}$
from
$D_{n+1}$
from
![]() $(\!-a, 0)$
is the point
$(\!-a, 0)$
is the point
![]() $r_{n+1} + 2\pi + 2\pi i(s_{n+1}+1)$
. Hence the square of the distance from
$r_{n+1} + 2\pi + 2\pi i(s_{n+1}+1)$
. Hence the square of the distance from
![]() $(\!-a, 0)$
to any point of
$(\!-a, 0)$
to any point of
![]() $D_{n+1}$
is at most
$D_{n+1}$
is at most
 \[(r_{n+1} + a + 2\pi)^2 + \left(2\pi(s_{n+1}+1)\right)^2 \leq r_{n+1}^2(1+\delta)^2 + r_{n+1}^2 \kappa^2 \leq r_{n+1}^2 \cdot \frac{c^2h_{\alpha}^2}{h_{\beta}^2},\]
\[(r_{n+1} + a + 2\pi)^2 + \left(2\pi(s_{n+1}+1)\right)^2 \leq r_{n+1}^2(1+\delta)^2 + r_{n+1}^2 \kappa^2 \leq r_{n+1}^2 \cdot \frac{c^2h_{\alpha}^2}{h_{\beta}^2},\]
where we have used (11), together with the choices of
![]() $\delta$
and
$\delta$
and
![]() $\kappa$
. Since the outer radius of
$\kappa$
. Since the outer radius of
![]() $A_n$
is
$A_n$
is
![]() $c h_{\alpha} g(r_n) = c h_{\alpha} r_{n+1} / h_{\beta}$
, this completes the proof of the claim.
$c h_{\alpha} g(r_n) = c h_{\alpha} r_{n+1} / h_{\beta}$
, this completes the proof of the claim.
It follows by, for example, [Reference Rippon and Stallard15, lemma 1], that there is point z such that
![]() $f^n(z) \in D_n$
, for
$f^n(z) \in D_n$
, for
![]() $n \in \mathbb{N}_0$
. Since
$n \in \mathbb{N}_0$
. Since
![]() $D_n \setminus T_{s_n}$
maps to the complement of H, we in fact have that
$D_n \setminus T_{s_n}$
maps to the complement of H, we in fact have that
![]() $f^n(z) \in T_{s_n}$
, for
$f^n(z) \in T_{s_n}$
, for
![]() $n \in \mathbb{N}_0$
. In other words,
$n \in \mathbb{N}_0$
. In other words,
![]() $z \in J_{\underline{s}}$
, which completes the proof.
$z \in J_{\underline{s}}$
, which completes the proof.
4. Devaney Hairs
Our goal in this section is to show that each component of J is a Devaney hair. Part (a) of Theorem 1·4 follows, since there are uncountably many g-bounded, and hence admissible, external addresses. Note that this requires that we establish the three properties (i), (ii) and (iii).
We first show that our function f satisfies a uniform head-start condition; this terminology is from [Reference Günter Rottenfusser, Rempe and Schleicher13]. This is a key ingredient in the arguments we use in the remainder of this paper. We require the following expansion estimate, which follows from (7); recall that
![]() $\mu > 1$
.
$\mu > 1$
.
Proposition 4·1 Suppose that f is a generalised exponential function, that
![]() $n \in {\mathbb{N}}$
, and that U is a component of
$n \in {\mathbb{N}}$
, and that U is a component of
![]() $f^{-n}({\mathbb{C}} \setminus \mathbb{H}_M)$
. Then
$f^{-n}({\mathbb{C}} \setminus \mathbb{H}_M)$
. Then
Proof. Let
![]() $\phi \,{:}\, {\mathbb{C}}\setminus\mathbb{H}_M \to U$
be the inverse to
$\phi \,{:}\, {\mathbb{C}}\setminus\mathbb{H}_M \to U$
be the inverse to
![]() $f^n$
. Since
$f^n$
. Since
![]() ${\mathbb{C}}\setminus\mathbb{H}_M$
is convex, it follows by (7) that, if
${\mathbb{C}}\setminus\mathbb{H}_M$
is convex, it follows by (7) that, if
![]() $z', w' \in {\mathbb{C}}\setminus\mathbb{H}_M$
, then
$z', w' \in {\mathbb{C}}\setminus\mathbb{H}_M$
, then
where [z
![]() $^{\prime}$
, w
$^{\prime}$
, w
![]() $^{\prime}$
] denotes the line segment from z
$^{\prime}$
] denotes the line segment from z
![]() $^{\prime}$
to w
$^{\prime}$
to w
![]() $^{\prime}$
. The result follows.
$^{\prime}$
. The result follows.
We now prove that f satisfies a uniform head-start condition.
Lemma 4·2. Suppose that f is generalised exponential function. Then there exists
![]() $K > 1$
with the following properties.
$K > 1$
with the following properties.
-
(i) Suppose that T, T
 $^{\prime}$
are tracts. If
$^{\prime}$
are tracts. If
 $z_0, z_1 \in \overline{T}$
and
$z_0, z_1 \in \overline{T}$
and
 $f(z_0), f(z_1) \in \overline{T'}$
, then
$f(z_0), f(z_1) \in \overline{T'}$
, then
 \[\operatorname{Re} z_1 \geq K \operatorname{Re} z_0 \implies \operatorname{Re} f(z_1) \geq K \operatorname{Re} f(z_0).\]
\[\operatorname{Re} z_1 \geq K \operatorname{Re} z_0 \implies \operatorname{Re} f(z_1) \geq K \operatorname{Re} f(z_0).\]
-
(ii) Suppose that
 $z_0, z_1$
have the same external address. Then there exist
$z_0, z_1$
have the same external address. Then there exist
 $k \in {\mathbb{N}}$
and
$k \in {\mathbb{N}}$
and
 $j \in \{0, 1\}$
such that
$j \in \{0, 1\}$
such that
 \[\operatorname{Re} f^p(z_j) \geq K \operatorname{Re} f^p(z_{1-j}), \quad\text{for } p \geq k.\]
\[\operatorname{Re} f^p(z_j) \geq K \operatorname{Re} f^p(z_{1-j}), \quad\text{for } p \geq k.\]
Proof. Note first that
and
First we prove (i). Suppose that T, T
![]() $^{\prime}$
are two tracts, that
$^{\prime}$
are two tracts, that
![]() $z_0, z_1 \in \overline{T}$
, and that
$z_0, z_1 \in \overline{T}$
, and that
![]() $f(z_0),$
$f(z_0),$
![]() $f(z_1) \in \overline{T'}$
. Suppose that
$f(z_1) \in \overline{T'}$
. Suppose that
![]() $q \in {\mathbb{N}}$
, that
$q \in {\mathbb{N}}$
, that
![]() $K \geq 2 \pi q$
, and finally that
$K \geq 2 \pi q$
, and finally that
![]() $\operatorname{Re} z_0 \geq K \operatorname{Re} z_1$
. Then, by (4) and (13),
$\operatorname{Re} z_0 \geq K \operatorname{Re} z_1$
. Then, by (4) and (13),
 \begin{align*}\operatorname{Re} f(z_1) &\geq |f(z_1)| - |\operatorname{Im} f(z_1)|, \\[3pt] &\geq h_{\alpha} g(\operatorname{Re} z_1) - a - |\operatorname{Im} f(z_0)| - \pi, \\[3pt] &\geq h_{\alpha} c^q g(\operatorname{Re} z_0) - a - |f(z_0)| - \pi.\end{align*}
\begin{align*}\operatorname{Re} f(z_1) &\geq |f(z_1)| - |\operatorname{Im} f(z_1)|, \\[3pt] &\geq h_{\alpha} g(\operatorname{Re} z_1) - a - |\operatorname{Im} f(z_0)| - \pi, \\[3pt] &\geq h_{\alpha} c^q g(\operatorname{Re} z_0) - a - |f(z_0)| - \pi.\end{align*}
We then consider two possibilities. Suppose first that
![]() $|f(z_0)| \geq 2a$
. It follows, by (12), that
$|f(z_0)| \geq 2a$
. It follows, by (12), that
![]() $g(\operatorname{Re} z_0) \geq ({|f(z_0)| - a})/{h_{\beta}} \geq ({1}/{2h_{\beta}})|f(z_0)|$
. Hence, since Re
$g(\operatorname{Re} z_0) \geq ({|f(z_0)| - a})/{h_{\beta}} \geq ({1}/{2h_{\beta}})|f(z_0)|$
. Hence, since Re
![]() $f(z_0) \geq M$
,
$f(z_0) \geq M$
,
On the other hand, if
![]() $|f(z_0)| < 2a$
, then
$|f(z_0)| < 2a$
, then
Since Re
![]() $f(z_0) \geq M$
, the conclusion (i) follows provided that q, and hence K, is chosen sufficiently large. (Note that the choice of q can be made independently of
$f(z_0) \geq M$
, the conclusion (i) follows provided that q, and hence K, is chosen sufficiently large. (Note that the choice of q can be made independently of
![]() $z_0$
and
$z_0$
and
![]() $z_1$
.)
$z_1$
.)
For (ii), suppose that
![]() $z_0\ne z_1$
have the same external address. Fix
$z_0\ne z_1$
have the same external address. Fix
![]() $p \in {\mathbb{N}}$
. Since
$p \in {\mathbb{N}}$
. Since
![]() $z_0$
and
$z_0$
and
![]() $z_1$
have the same external address, there exists a component U of
$z_1$
have the same external address, there exists a component U of
![]() $f^{-p}({\mathbb{C}}\setminus\mathbb{H}_M)$
, containing both
$f^{-p}({\mathbb{C}}\setminus\mathbb{H}_M)$
, containing both
![]() $z_0$
and
$z_0$
and
![]() $z_1$
, that maps injectively to
$z_1$
, that maps injectively to
![]() ${\mathbb{C}}\setminus\mathbb{H}_M$
. It follows by Proposition 4·1 that
${\mathbb{C}}\setminus\mathbb{H}_M$
. It follows by Proposition 4·1 that
![]() $|f^p(z_0) - f^p(z_1)| \geq \mu^p |z_0 - z_1|$
. The result then follows by (i), since
$|f^p(z_0) - f^p(z_1)| \geq \mu^p |z_0 - z_1|$
. The result then follows by (i), since
![]() $f^p(z_0)$
and
$f^p(z_0)$
and
![]() $f^p(z_1)$
lie in the same tract, and p was arbitrary.
$f^p(z_1)$
lie in the same tract, and p was arbitrary.
Next we use the uniform head-start condition to prove the existence of unbounded simple curves in J; in other words, we prove that J consists of simple curves that satisfy (i) and (ii). We defer the proof of (iii) until a little later.
Next we introduce a so-called speed ordering. For each
![]() $z,w \in J_{\underline{s}}$
we say that
$z,w \in J_{\underline{s}}$
we say that
![]() $z \succ w$
if there exists
$z \succ w$
if there exists
![]() $k \in {\mathbb{N}}$
with the property that
$k \in {\mathbb{N}}$
with the property that
![]() $ \operatorname{Re}f^k(z) > K \operatorname{Re}f^k(w)$
, where
$ \operatorname{Re}f^k(z) > K \operatorname{Re}f^k(w)$
, where
![]() $K>1$
is the constant from Lemma 4·2. We extend this order to the closure of
$K>1$
is the constant from Lemma 4·2. We extend this order to the closure of
![]() $J_{\underline{s}}$
in
$J_{\underline{s}}$
in
![]() $\hat{{\mathbb{C}}}$
, which we denote by
$\hat{{\mathbb{C}}}$
, which we denote by
![]() $\hat{J_{\underline{s}}}$
, by the convention that
$\hat{J_{\underline{s}}}$
, by the convention that
![]() $\infty \succ z$
for all
$\infty \succ z$
for all
![]() $z \in J_{\underline{s}}$
. We then have the following.
$z \in J_{\underline{s}}$
. We then have the following.
Lemma 4·3 Suppose that f is a generalised exponential function, and that
![]() $\underline{s}$
is an admissible external address. Then
$\underline{s}$
is an admissible external address. Then
![]() $\big(\hat{J_{\underline{s}}}, \succ\!\big)$
is a totally ordered space, and
$\big(\hat{J_{\underline{s}}}, \succ\!\big)$
is a totally ordered space, and
![]() $J_{\underline{s}}$
has a unique unbounded component, which is a simple closed arc to infinity.
$J_{\underline{s}}$
has a unique unbounded component, which is a simple closed arc to infinity.
Proof. The fact that
![]() $\big(\hat{J_{\underline{s}}}, \succ\!\big)$
is a totally ordered space is a straightforward consequence of Lemma 4·2.
$\big(\hat{J_{\underline{s}}}, \succ\!\big)$
is a totally ordered space is a straightforward consequence of Lemma 4·2.
We then claim that each component of
![]() $\hat{J_{\underline{s}}}$
is homeomorphic to a compact interval, which may be degenerate. The proof of this fact is exactly as in the proof of [Reference Günter Rottenfusser, Rempe and Schleicher13, proposition 4·4(a)]; it is first shown that the identity map from
$\hat{J_{\underline{s}}}$
is homeomorphic to a compact interval, which may be degenerate. The proof of this fact is exactly as in the proof of [Reference Günter Rottenfusser, Rempe and Schleicher13, proposition 4·4(a)]; it is first shown that the identity map from
![]() $\hat{J_{\underline{s}}}$
to
$\hat{J_{\underline{s}}}$
to
![]() $\big(\hat{J_{\underline{s}}}, \succ\!\big)$
is continuous, and the result then follows from a well-known characterisation of an arc. We omit the details.
$\big(\hat{J_{\underline{s}}}, \succ\!\big)$
is continuous, and the result then follows from a well-known characterisation of an arc. We omit the details.
Now, since
![]() $\underline{s}$
is admissible, we know that
$\underline{s}$
is admissible, we know that
![]() $J_{\underline{s}} \ne \emptyset$
. We also know, by Proposition 3·2, that each component of
$J_{\underline{s}} \ne \emptyset$
. We also know, by Proposition 3·2, that each component of
![]() $J_{\underline{s}}$
is unbounded. Uniqueness then follows from the fact that
$J_{\underline{s}}$
is unbounded. Uniqueness then follows from the fact that
![]() $\infty$
is the maximal element of
$\infty$
is the maximal element of
![]() $\big(\hat{J_{\underline{s}}}, \succ\!\big)$
.
$\big(\hat{J_{\underline{s}}}, \succ\!\big)$
.
Note that (i) and (ii) and are now an immediate consequence of Lemma 4·3, together with Observation 3·4. It remains to show that the uniform escape property (iii) holds on the components of J. In fact, this is a consequence of Lemma 4·3, together with the following.
Lemma 4·4 Suppose that f is a generalised exponential function. If
![]() $z,w \in J$
have the same external address, then
$z,w \in J$
have the same external address, then
Proof. We omit the proof of this lemma, which is essentially the same as the proof of [Reference Günter Rottenfusser, Rempe and Schleicher13, lemma 3·2], using Proposition 4·1 to give expansion.
5. Cantor bouquets
In this section we show that J is a Cantor bouquet; in other words, we prove part (b) of Theorem 1·4. It was observed in [Reference Alhabib and Rempe-Gillen2] that the result of [Reference Mayer10] holds for all Cantor bouquets. Hence part (c) of Theorem 1·4 is a direct consequence of this. Note that the arguments in this section are essentially topological, and very similar to those of [Reference Barański, Jarque and Rempe5]. Accordingly we give only brief details, and refer to that paper for more detailed explanations and definitions.
In fact, we shall construct a so-called one-sided hairy arc. This is a topological object defined as follows (see also [Reference Aarts and Oversteegen1] and [Reference Barański, Jarque and Rempe5]).
Definition 5·1 A one-sided hairy arc is a continuum
![]() $X \subset {\mathbb{R}}^2$
containing an arc B (called the base of X), and a total order
$X \subset {\mathbb{R}}^2$
containing an arc B (called the base of X), and a total order
![]() $\prec$
on B, such that:
$\prec$
on B, such that:
-
(i) the closure of every connected component of
 $X \setminus B$
is an arc, with exactly one endpoint in B. In particular, for each
$X \setminus B$
is an arc, with exactly one endpoint in B. In particular, for each
 $x \in X \setminus B$
, there exists a unique arc
$x \in X \setminus B$
, there exists a unique arc
 $\gamma_x \,{:}\,[0,1] \to X$
such that
$\gamma_x \,{:}\,[0,1] \to X$
such that
 $\gamma_x(0)=x$
,
$\gamma_x(0)=x$
,
 $\gamma_x(t)\notin B$
for
$\gamma_x(t)\notin B$
for
 $t <1$
, and
$t <1$
, and
 $\gamma_x(1) \in B$
. In this case, we say that x belongs to the hair attached at
$\gamma_x(1) \in B$
. In this case, we say that x belongs to the hair attached at
 $\gamma_x(1)$
.
$\gamma_x(1)$
. -
(ii) all the hairs are attached at the same side of the base.
-
(iii) distinct components of
 $X \setminus B$
have disjoint closures, and
$X \setminus B$
have disjoint closures, and
 $X \setminus B$
is dense in X.
$X \setminus B$
is dense in X. -
(iv) if
 $x_0 \in X \setminus B$
and
$x_0 \in X \setminus B$
and
 $x_n \in X \setminus B$
is a sequence of points converging to
$x_n \in X \setminus B$
is a sequence of points converging to
 $x_0$
, then
$x_0$
, then
 $\gamma_{x_n} \rightarrow \gamma_{x_0}$
in the Hausdorff metric.
$\gamma_{x_n} \rightarrow \gamma_{x_0}$
in the Hausdorff metric. -
(v) if
 $b \in B$
and x belongs to the hair attached at b, then there exist sequences
$b \in B$
and x belongs to the hair attached at b, then there exist sequences
 $x^+_n, x^-_n$
, attached respectively at points
$x^+_n, x^-_n$
, attached respectively at points
 $b^+_n, b^-_n \in B$
, such that
$b^+_n, b^-_n \in B$
, such that
 $b^-_n \prec b \prec b^+_n$
and
$b^-_n \prec b \prec b^+_n$
and
 $x^-_n, x^+_n \rightarrow x$
as
$x^-_n, x^+_n \rightarrow x$
as
 $n\rightarrow\infty$
.
$n\rightarrow\infty$
.
It is known that if X is a one-sided hairy arc, then
![]() $X \setminus B$
is homeomorphic to a topological object known as a straight brush; we omit the definition, which can be found at [Reference Aarts and Oversteegen1]. Our goal is to construct a suitable base B so that
$X \setminus B$
is homeomorphic to a topological object known as a straight brush; we omit the definition, which can be found at [Reference Aarts and Oversteegen1]. Our goal is to construct a suitable base B so that
![]() $J \cup B$
is a one-sided hairy arc. Since a Cantor bouquet is, by definition, a set ambiently homeomorphic to a straight brush, the result follows.
$J \cup B$
is a one-sided hairy arc. Since a Cantor bouquet is, by definition, a set ambiently homeomorphic to a straight brush, the result follows.
We follow the construction in [Reference Barański, Jarque and Rempe5, section 5], although our construction is slightly easier since (up to
![]() $2 \pi i$
translation) we only have one tract. First we define intermediate addresses, which are used in our construction. Let
$2 \pi i$
translation) we only have one tract. First we define intermediate addresses, which are used in our construction. Let
![]() $\mathcal{T}$
denote the set of tracts of f equipped with a natural total order.
$\mathcal{T}$
denote the set of tracts of f equipped with a natural total order.
Definition 5·2 For
![]() $k \in {\mathbb{Z}}$
, an intermediate entry is a pair
$k \in {\mathbb{Z}}$
, an intermediate entry is a pair
![]() $(k,k+1)$
where
$(k,k+1)$
where
![]() $T_k, T_{k+1} \in \mathcal{T}$
are consecutive tracts with respect to the total order of tracts.
$T_k, T_{k+1} \in \mathcal{T}$
are consecutive tracts with respect to the total order of tracts.
Note that this procedure of considering intermediate entries simply adds an intermediate entry between any pair of adjacent tracts. Now we can define intermediate external addresses as follows.
Definition 5·3 A (finite) sequence
![]() $\underline{s} = T_0 T_1\cdots T_{n-1}S_n$
, where
$\underline{s} = T_0 T_1\cdots T_{n-1}S_n$
, where
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $T_j\in \mathcal{T}$
for
$T_j\in \mathcal{T}$
for
![]() $0 \leq j \leq n-1$
, and where
$0 \leq j \leq n-1$
, and where
![]() $S_n$
is an intermediate entry, is called an intermediate external address.
$S_n$
is an intermediate entry, is called an intermediate external address.
We now define B to be the union of:
-
(i) the set
 ${\mathbb{Z}}^{{\mathbb{N}}_0}$
of all external addresses;
${\mathbb{Z}}^{{\mathbb{N}}_0}$
of all external addresses; -
(ii) the set of all intermediate external addresses;
-
(iii) the set
 $\{-\infty, \infty\}$
.
$\{-\infty, \infty\}$
.
We then let
![]() $\tilde{H}= \overline{H}\cup B$
; recall that H is the image of the tracts, defined in (9). Exactly as in [Reference Barański, Jarque and Rempe5, section 5] we can define a topology on
$\tilde{H}= \overline{H}\cup B$
; recall that H is the image of the tracts, defined in (9). Exactly as in [Reference Barański, Jarque and Rempe5, section 5] we can define a topology on
![]() $\tilde{H}$
by specifying a neighbourhood base for every
$\tilde{H}$
by specifying a neighbourhood base for every
![]() $\underline{s} \in B$
. It then follows from [Reference Barański, Jarque and Rempe5, Proposition 5·6], that
$\underline{s} \in B$
. It then follows from [Reference Barański, Jarque and Rempe5, Proposition 5·6], that
![]() $\tilde{H}$
is homeomorphic to the closed unit disc, and B is homeomorphic to an arc.
$\tilde{H}$
is homeomorphic to the closed unit disc, and B is homeomorphic to an arc.
First, we show that the set of admissible external addresses (see Definition 3·3) is dense in the set of all external addresses.
Proposition 5·4 The set of admissible external addresses is dense in
![]() ${\mathbb{Z}}_{{\mathbb{N}}_0}$
.
${\mathbb{Z}}_{{\mathbb{N}}_0}$
.
Proof. We know from Theorem 3·6 that g-bounded external addresses are admissible. Hence, since periodic external addresses are certainly g-bounded, we deduce that periodic external addresses are admissible. The result follows since periodic external addresses are dense in
![]() ${\mathbb{Z}}_{{\mathbb{N}}_0}$
.
${\mathbb{Z}}_{{\mathbb{N}}_0}$
.
Let
![]() $\kern2pt\tilde{\kern-2pt J}$
denote the closure of J in the space
$\kern2pt\tilde{\kern-2pt J}$
denote the closure of J in the space
![]() $\tilde{H}$
. Our goal is to show that
$\tilde{H}$
. Our goal is to show that
![]() $\kern2pt\tilde{\kern-2pt J}$
is a one-sided hairy arc. To achieve this we need some results which together imply that properties (i)-(v) from definition 5·1 hold.
$\kern2pt\tilde{\kern-2pt J}$
is a one-sided hairy arc. To achieve this we need some results which together imply that properties (i)-(v) from definition 5·1 hold.
Proposition 5·5. The set
![]() $\kern2pt\tilde{\kern-2pt J}$
is a continuum with
$\kern2pt\tilde{\kern-2pt J}$
is a continuum with
![]() $J = \kern2pt\tilde{\kern-2pt J} \setminus B$
. Moreover, the closure of every component of J is an arc, with exactly one endpoint in B, distinct components of J have disjoint closures in
$J = \kern2pt\tilde{\kern-2pt J} \setminus B$
. Moreover, the closure of every component of J is an arc, with exactly one endpoint in B, distinct components of J have disjoint closures in
![]() $\kern2pt\tilde{\kern-2pt J}$
, and J is dense in
$\kern2pt\tilde{\kern-2pt J}$
, and J is dense in
![]() $\kern2pt\tilde{\kern-2pt J}$
.
$\kern2pt\tilde{\kern-2pt J}$
.
We know that B is an arc. Note that this proposition gives properties (i) and (iii). Moreover,
![]() $\kern2pt\tilde{\kern-2pt J}$
is one-sided by construction, hence property (ii) is satisfied.
$\kern2pt\tilde{\kern-2pt J}$
is one-sided by construction, hence property (ii) is satisfied.
Proof of Proposition 5·5. Recall from Lemma 4·3 that each component of J is a simple closed arc to infinity,
![]() $J_{\underline{s}}$
, for some external address
$J_{\underline{s}}$
, for some external address
![]() $\underline{s}$
. Suppose that
$\underline{s}$
. Suppose that
![]() $\underline{s}$
is an admissible external address. We can deduce from the topology on
$\underline{s}$
is an admissible external address. We can deduce from the topology on
![]() $\tilde{H}$
that points of
$\tilde{H}$
that points of
![]() $J_{\underline{s}}$
cannot accumulate on any element of B apart from
$J_{\underline{s}}$
cannot accumulate on any element of B apart from
![]() $\underline{s}$
. Hence
$\underline{s}$
. Hence
![]() $J_{\underline{s}} \cup \{\underline{s}\}$
is a compact subset of
$J_{\underline{s}} \cup \{\underline{s}\}$
is a compact subset of
![]() $\tilde{H}$
. Moreover,
$\tilde{H}$
. Moreover,
![]() $J_{\underline{s}} \cup \{\underline{s}\}$
is connected.
$J_{\underline{s}} \cup \{\underline{s}\}$
is connected.
It follows from Proposition 5·4 that
![]() $B \subset \kern2pt\tilde{\kern-2pt J}$
. Hence
$B \subset \kern2pt\tilde{\kern-2pt J}$
. Hence
![]() $\kern2pt\tilde{\kern-2pt J}$
is the disjoint union
$\kern2pt\tilde{\kern-2pt J}$
is the disjoint union
where the union is taken over the admissible external addresses.
B is homeomorphic to an arc, and so connected. Also,
![]() $\tilde{H}$
is a compact metric space, and hence so is
$\tilde{H}$
is a compact metric space, and hence so is
![]() $\kern2pt\tilde{\kern-2pt J}$
. The claims of the proposition follow from these facts, together with (14).
$\kern2pt\tilde{\kern-2pt J}$
. The claims of the proposition follow from these facts, together with (14).
In order to prove the accumulation of hairs, i.e., property (v), we use the following result.
Proposition 5·6. Suppose that
![]() $z_0 \in J$
. Then there are sequences
$z_0 \in J$
. Then there are sequences
![]() $z^-_n , z^+_n \in J$
, with
$z^-_n , z^+_n \in J$
, with
![]() $\operatorname{addr}(z^-_n) < \operatorname{addr}(z_0) < \operatorname{addr}(z^+_n)$
, for
$\operatorname{addr}(z^-_n) < \operatorname{addr}(z_0) < \operatorname{addr}(z^+_n)$
, for
![]() $n \in{\mathbb{N}}$
, and
$n \in{\mathbb{N}}$
, and
![]() $z^-_n \rightarrow z_0$
,
$z^-_n \rightarrow z_0$
,
![]() $z^+_n \rightarrow z_0$
as
$z^+_n \rightarrow z_0$
as
![]() $n \rightarrow\infty$
.
$n \rightarrow\infty$
.
Proof. Choose
![]() $p \in {\mathbb{N}}$
. Let U be the component of
$p \in {\mathbb{N}}$
. Let U be the component of
![]() $f^{-p}(H)$
containing
$f^{-p}(H)$
containing
![]() $z_0$
, and let
$z_0$
, and let
![]() $\phi \,{:}\, H \to U$
be the inverse to
$\phi \,{:}\, H \to U$
be the inverse to
![]() $f^{-p}$
. Define a pair of points
$f^{-p}$
. Define a pair of points
![]() $z^\pm_p = \phi(f^p(z_0) \pm 2 \pi i)$
, so that, by definition, we have
$z^\pm_p = \phi(f^p(z_0) \pm 2 \pi i)$
, so that, by definition, we have
![]() $\operatorname{addr}(z^-_p) < \operatorname{addr}(z_0) < \operatorname{addr}(z^+_p)$
, for
$\operatorname{addr}(z^-_p) < \operatorname{addr}(z_0) < \operatorname{addr}(z^+_p)$
, for
![]() $p \in {\mathbb{N}}$
. It follows by Proposition 4·1 that
$p \in {\mathbb{N}}$
. It follows by Proposition 4·1 that
![]() $z^\pm_n \rightarrow z_0$
as
$z^\pm_n \rightarrow z_0$
as
![]() $n \rightarrow \infty$
, as required.
$n \rightarrow \infty$
, as required.
The following proposition is analogous to [Reference Barański, Jarque and Rempe5, proposition 6·1] and we omit the proof.
Proposition 5·7. Suppose that
![]() $a_n \in J$
converges to a point
$a_n \in J$
converges to a point
![]() $a \in J$
, and that, for each n,
$a \in J$
, and that, for each n,
![]() $b_n \in J_{addr(a_n)}$
has the same external address as
$b_n \in J_{addr(a_n)}$
has the same external address as
![]() $a_n$
and satisfies
$a_n$
and satisfies
![]() $b_n \succ a_n$
in the speed ordering of f. If
$b_n \succ a_n$
in the speed ordering of f. If
![]() $b \in J$
is an accumulation point of the sequence
$b \in J$
is an accumulation point of the sequence
![]() $b_n$
, then
$b_n$
, then
![]() $b \succ a$
.
$b \succ a$
.
We use Proposition 5·7 as a tool to prove property (iv), as shown below.
Proposition 5·8. If
![]() $x_0 \in X \setminus B$
and
$x_0 \in X \setminus B$
and
![]() $x_n \in X \setminus B$
is a sequence of points converging to
$x_n \in X \setminus B$
is a sequence of points converging to
![]() $x_0$
, then
$x_0$
, then
![]() $\gamma_{x_n} \rightarrow \gamma_{x_0}$
in the Hausdorff metric.
$\gamma_{x_n} \rightarrow \gamma_{x_0}$
in the Hausdorff metric.
Proof. Passing to a subsequence, we may assume that
![]() $\gamma_{x_n}$
converges in the Hausdorff metric to a limit
$\gamma_{x_n}$
converges in the Hausdorff metric to a limit
![]() $\gamma$
. Then
$\gamma$
. Then
![]() $\gamma \subset J_{\underline{s}}\cup \{s\},$
where
$\gamma \subset J_{\underline{s}}\cup \{s\},$
where
![]() $\underline{s}= \operatorname{addr}(z_0)$
. Note that
$\underline{s}= \operatorname{addr}(z_0)$
. Note that
![]() $\gamma$
is connected as the Hausdorff limit of compact connected subsets of the compact space
$\gamma$
is connected as the Hausdorff limit of compact connected subsets of the compact space
![]() $\kern2pt\tilde{\kern-2pt J}$
, and also it contains both
$\kern2pt\tilde{\kern-2pt J}$
, and also it contains both
![]() $z_0$
and
$z_0$
and
![]() $\underline{s}$
. Hence we have that
$\underline{s}$
. Hence we have that
![]() $\gamma_{z_0} \subset \gamma.$
It remains to show that
$\gamma_{z_0} \subset \gamma.$
It remains to show that
![]() $\gamma \subset \gamma_{z_0}$
. Note that this inclusion follows from Proposition 5·7.
$\gamma \subset \gamma_{z_0}$
. Note that this inclusion follows from Proposition 5·7.
We have shown that
![]() $\kern2pt\tilde{\kern-2pt J} = J \cup B$
is a one-sided hairy arc. Hence, for the reasons noted earlier, J is a Cantor bouquet, which completes the proof of Theorem 1·4.
$\kern2pt\tilde{\kern-2pt J} = J \cup B$
is a one-sided hairy arc. Hence, for the reasons noted earlier, J is a Cantor bouquet, which completes the proof of Theorem 1·4.
Acknowledgment
We are grateful to the referee for a careful reading and much helpful feedback.