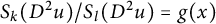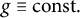1 Introduction
In this paper, we study the exterior Dirichlet problem of the Hessian quotient equation
 $$ \begin{align} \frac{S_k(D^2u)}{S_l(D^2u)}=g(x) &\quad \mbox{in}\ \ \mathbb{R}^n\setminus\bar{\Omega}, \end{align} $$
$$ \begin{align} \frac{S_k(D^2u)}{S_l(D^2u)}=g(x) &\quad \mbox{in}\ \ \mathbb{R}^n\setminus\bar{\Omega}, \end{align} $$
where
![]() $n\geq 2$
,
$n\geq 2$
,
![]() $0\leq l<k\leq n$
,
$0\leq l<k\leq n$
,
![]() $\Omega $
is a smooth, bounded, strictly convex open set in
$\Omega $
is a smooth, bounded, strictly convex open set in
![]() ${\mathbb R}^{n}$
,
${\mathbb R}^{n}$
,
![]() $\phi \in C^2(\partial \Omega )$
,
$\phi \in C^2(\partial \Omega )$
,
![]() $0<g\in C^{0}(\mathbb {R}^{n}\backslash \Omega )$
,
$0<g\in C^{0}(\mathbb {R}^{n}\backslash \Omega )$
,
![]() $S_0(D^2u):=\sigma _0(\lambda (D^2u)):=1$
,
$S_0(D^2u):=\sigma _0(\lambda (D^2u)):=1$
,
denotes the jth elementary symmetric function of
![]() $\lambda (D^2u)=(\lambda _1,\lambda _2,\dots ,\lambda _n)$
, the eigenvalues of the Hessian matrix of u.
$\lambda (D^2u)=(\lambda _1,\lambda _2,\dots ,\lambda _n)$
, the eigenvalues of the Hessian matrix of u.
Equation (1.1) has received a lot of attentions since the classical work of Caffarelli, Nirenberg, and Spruck [Reference Caffarelli, Nirenberg and Spruck7] and Trudinger [Reference Trudinger22]. For
![]() $l=0$
, it is the k-Hessian equation. In particular, if
$l=0$
, it is the k-Hessian equation. In particular, if
![]() $k=1$
, it is the Poisson equation, while it is the Monge–Ampère equation if
$k=1$
, it is the Poisson equation, while it is the Monge–Ampère equation if
![]() $k=n$
. For
$k=n$
. For
![]() $n=k=3$
and
$n=k=3$
and
![]() $l=1$
, it is the special Lagrangian equation which is closely connected with geometric problems: If u satisfies
$l=1$
, it is the special Lagrangian equation which is closely connected with geometric problems: If u satisfies
![]() $\mbox {det} D^2u=\Delta u$
in
$\mbox {det} D^2u=\Delta u$
in
![]() $\mathbb {R}^3$
, then the graph of
$\mathbb {R}^3$
, then the graph of
![]() $Du$
in
$Du$
in
![]() $\mathbb {C}^3$
is a special Lagrangian submanifold, that is, its mean curvature vanishes everywhere and the complex structure on
$\mathbb {C}^3$
is a special Lagrangian submanifold, that is, its mean curvature vanishes everywhere and the complex structure on
![]() $\mathbb {C}^3$
sends the tangent space of the graph to the normal space at every point.
$\mathbb {C}^3$
sends the tangent space of the graph to the normal space at every point.
A classical theorem of Jörgens (
![]() $n=2$
) [Reference Jörgens15], Calabi (
$n=2$
) [Reference Jörgens15], Calabi (
![]() $n\leq 5$
) [Reference Calabi8], and Pogorelov (
$n\leq 5$
) [Reference Calabi8], and Pogorelov (
![]() $n\geq 2$
) [Reference Pogorelov21] states that any convex classical solution of
$n\geq 2$
) [Reference Pogorelov21] states that any convex classical solution of
![]() $\det D^2u=1$
in
$\det D^2u=1$
in
![]() $\mathbb {R}^n$
must be a quadratic polynomial. Caffarelli and Li [Reference Caffarelli and Li6] extended the Jörgens–Calabi–Pogorelov theorem and studied the existence of solutions of Monge–Ampère equations in exterior domains with prescribed asymptotic behavior. They proved that for
$\mathbb {R}^n$
must be a quadratic polynomial. Caffarelli and Li [Reference Caffarelli and Li6] extended the Jörgens–Calabi–Pogorelov theorem and studied the existence of solutions of Monge–Ampère equations in exterior domains with prescribed asymptotic behavior. They proved that for
![]() $n\geq 3$
, given any
$n\geq 3$
, given any
![]() $b\in \mathbb {R}^n$
and any
$b\in \mathbb {R}^n$
and any
![]() $n\times n$
real symmetric positive definite matrix A with
$n\times n$
real symmetric positive definite matrix A with
![]() $\det A=1$
, there exists some constant
$\det A=1$
, there exists some constant
![]() $c^*$
depending on n,
$c^*$
depending on n,
![]() $\Omega $
,
$\Omega $
,
![]() $\phi $
, b, and A such that for every
$\phi $
, b, and A such that for every
![]() $c>c^*$
, the Monge–Ampère equation
$c>c^*$
, the Monge–Ampère equation
![]() $\det D^2u=1$
in
$\det D^2u=1$
in
![]() ${\mathbb R}^{n}\setminus \bar {\Omega }$
with the Dirichlet boundary condition (1.2) and the following prescribed asymptotic behavior at infinity
${\mathbb R}^{n}\setminus \bar {\Omega }$
with the Dirichlet boundary condition (1.2) and the following prescribed asymptotic behavior at infinity
admits a unique viscosity solution
![]() $u\in C^{\infty }(\mathbb {R}^n\setminus \bar {\Omega })\cap C^0(\mathbb {R}^n\setminus \Omega )$
. Based on this work, Li and Lu [Reference Li and Lu19] completed the characterization of the existence and non-existence of solutions in terms of the above asymptotic behaviors. For more results concerning the exterior Dirichlet problem for Monge–Ampère equations, we refer to [Reference Bao and Li1, Reference Bao, Li and Zhang3–Reference Bao, Xiong and Zhou5, Reference Hong13] and the references therein.
$u\in C^{\infty }(\mathbb {R}^n\setminus \bar {\Omega })\cap C^0(\mathbb {R}^n\setminus \Omega )$
. Based on this work, Li and Lu [Reference Li and Lu19] completed the characterization of the existence and non-existence of solutions in terms of the above asymptotic behaviors. For more results concerning the exterior Dirichlet problem for Monge–Ampère equations, we refer to [Reference Bao and Li1, Reference Bao, Li and Zhang3–Reference Bao, Xiong and Zhou5, Reference Hong13] and the references therein.
After the work of Caffarelli and Li [Reference Caffarelli and Li6], there have been extensive studies on the existence of fully nonlinear elliptic equations in exterior domains.
For the exterior Dirichlet problem of the Hessian equations, Dai and Bao [Reference Dai and Bao12] first obtained the existence of solutions satisfying the asymptotic behavior (1.3) with
![]() $A=(1/\binom {n}{k})^{\frac {1}{k}}I$
. Later on, Bao, Li, and Li [Reference Bao, Li and Li2] proved that for
$A=(1/\binom {n}{k})^{\frac {1}{k}}I$
. Later on, Bao, Li, and Li [Reference Bao, Li and Li2] proved that for
![]() $n\geq 3$
, given any
$n\geq 3$
, given any
![]() $b\in \mathbb {R}^n$
and any
$b\in \mathbb {R}^n$
and any
![]() $n\times n$
real symmetric positive definite matrix A with
$n\times n$
real symmetric positive definite matrix A with
![]() $S_{k}(A)=1$
, there exists some constant
$S_{k}(A)=1$
, there exists some constant
![]() $c^*$
depending on n,
$c^*$
depending on n,
![]() $\Omega $
,
$\Omega $
,
![]() $\phi $
, b, and A such that for every
$\phi $
, b, and A such that for every
![]() $c>c^*$
, the Hessian equation
$c>c^*$
, the Hessian equation
![]() $S_k(D^2u)=1$
in
$S_k(D^2u)=1$
in
![]() ${\mathbb R}^{n}\setminus \bar {\Omega }$
with the Dirichlet boundary condition (1.2) and the following prescribed asymptotic behavior at infinity
${\mathbb R}^{n}\setminus \bar {\Omega }$
with the Dirichlet boundary condition (1.2) and the following prescribed asymptotic behavior at infinity
admits a unique viscosity solution
![]() $u\in C^{\infty }(\mathbb {R}^n\setminus \bar {\Omega })\cap C^0(\mathbb {R}^n\setminus \Omega )$
, where
$u\in C^{\infty }(\mathbb {R}^n\setminus \bar {\Omega })\cap C^0(\mathbb {R}^n\setminus \Omega )$
, where
![]() $\theta \in [\frac {k-2}{n-2},1]$
is a constant depending on
$\theta \in [\frac {k-2}{n-2},1]$
is a constant depending on
![]() $n, k$
, and A. For more results concerning the exterior Dirichlet problem for Hessian equations, we refer to [Reference Cao and Bao9, Reference Dai10] and the references therein.
$n, k$
, and A. For more results concerning the exterior Dirichlet problem for Hessian equations, we refer to [Reference Cao and Bao9, Reference Dai10] and the references therein.
For the exterior Dirichlet problem of the Hessian quotient equation (1.1) with
![]() $g\equiv 1$
and the Dirichlet boundary condition (1.2), Dai [Reference Dai11] first obtained the existence of solutions with asymptotic behavior
$g\equiv 1$
and the Dirichlet boundary condition (1.2), Dai [Reference Dai11] first obtained the existence of solutions with asymptotic behavior
where
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $\bar {c}=(\binom {n}{l}/\binom {n}{k})^{\frac {1}{k-l}}$
, and
$\bar {c}=(\binom {n}{l}/\binom {n}{k})^{\frac {1}{k-l}}$
, and
![]() $k-l\geq 3$
. Subsequently, Li and Dai [Reference Li and Dai17] obtained the existence result for the case
$k-l\geq 3$
. Subsequently, Li and Dai [Reference Li and Dai17] obtained the existence result for the case
![]() $k-l=1$
and
$k-l=1$
and
![]() $k-l=2$
. Later on, Li and Li [Reference Li and Li16] proved that for
$k-l=2$
. Later on, Li and Li [Reference Li and Li16] proved that for
![]() $n\geq 3$
and, given any
$n\geq 3$
and, given any
![]() $b\in \mathbb {R}^n$
and any A in the set
$b\in \mathbb {R}^n$
and any A in the set
with
![]() $\frac {k-l}{\overline {t}_k-\underline {t}_l}>2$
, where
$\frac {k-l}{\overline {t}_k-\underline {t}_l}>2$
, where
 $$ \begin{align} \overline{t}_{k}:=\max_{1\leq i\leq n}\dfrac{\frac{\partial}{\partial\lambda_i} \sigma_{k}(\lambda(A))\lambda_i}{\sigma_k(\lambda(A))}=\max_{1\leq i\leq n}\dfrac{\sigma_{k-1;i}(\lambda)\lambda_i}{\sigma_k(\lambda)}, \end{align} $$
$$ \begin{align} \overline{t}_{k}:=\max_{1\leq i\leq n}\dfrac{\frac{\partial}{\partial\lambda_i} \sigma_{k}(\lambda(A))\lambda_i}{\sigma_k(\lambda(A))}=\max_{1\leq i\leq n}\dfrac{\sigma_{k-1;i}(\lambda)\lambda_i}{\sigma_k(\lambda)}, \end{align} $$
and
 $$ \begin{align} \underline{t}_{k}:=\min_{1\leq i\leq n}\dfrac{\frac{\partial}{\partial\lambda_i} \sigma_{k}(\lambda(A))\lambda_i}{\sigma_k(\lambda(A))}=\min_{1\leq i\leq n}\dfrac{\sigma_{k-1;i}(\lambda)\lambda_i}{\sigma_k(\lambda)}, \end{align} $$
$$ \begin{align} \underline{t}_{k}:=\min_{1\leq i\leq n}\dfrac{\frac{\partial}{\partial\lambda_i} \sigma_{k}(\lambda(A))\lambda_i}{\sigma_k(\lambda(A))}=\min_{1\leq i\leq n}\dfrac{\sigma_{k-1;i}(\lambda)\lambda_i}{\sigma_k(\lambda)}, \end{align} $$
there exists some constant
![]() $c^*$
depending on n, k, l,
$c^*$
depending on n, k, l,
![]() $\Omega $
,
$\Omega $
,
![]() $\phi $
, b, and A such that for every
$\phi $
, b, and A such that for every
![]() $c>c^*$
, the Hessian equation
$c>c^*$
, the Hessian equation
![]() $S_k(D^2u)/S_{l}(D^{2}u)=1$
in
$S_k(D^2u)/S_{l}(D^{2}u)=1$
in
![]() ${\mathbb R}^{n}\setminus \bar {\Omega }$
with the Dirichlet boundary condition (1.2) and the following prescribed asymptotic behavior at infinity
${\mathbb R}^{n}\setminus \bar {\Omega }$
with the Dirichlet boundary condition (1.2) and the following prescribed asymptotic behavior at infinity
admits a unique viscosity solution
![]() $u\in C^0(\mathbb {R}^n\setminus \Omega )$
, where
$u\in C^0(\mathbb {R}^n\setminus \Omega )$
, where
![]() $m\in (2,n]$
is a constant depending on
$m\in (2,n]$
is a constant depending on
![]() $n, k$
, l, and A. Recently, we have just learned that Jiang, Li, and Li [Reference Jiang, Li and Li14] generalized this result to
$n, k$
, l, and A. Recently, we have just learned that Jiang, Li, and Li [Reference Jiang, Li and Li14] generalized this result to
![]() $g=1+O(r^{-\beta })$
with
$g=1+O(r^{-\beta })$
with
![]() $\beta>2$
. For more results concerning the exterior Dirichlet problem for Hessian equations, we refer to [Reference Li, Li and Zhao18] and the references therein.
$\beta>2$
. For more results concerning the exterior Dirichlet problem for Hessian equations, we refer to [Reference Li, Li and Zhao18] and the references therein.
Our paper consists of two parts. In the first part, we obtain the necessary and sufficient conditions on the existence of radially symmetric solutions of the exterior Dirichlet problem of Hessian quotient equations.
Before stating our result of the first part, we first give the definition of k-convex functions. For
![]() $k=1$
,
$k=1$
,
![]() $2$
,
$2$
,
![]() $\dots $
, n, we say a
$\dots $
, n, we say a
![]() $C^{2}$
function u defined in a domain is k-convex (uniformly k-convex), if
$C^{2}$
function u defined in a domain is k-convex (uniformly k-convex), if
![]() $\lambda (D^{2}u)\in \bar {\Gamma }_{k}$
(
$\lambda (D^{2}u)\in \bar {\Gamma }_{k}$
(
![]() $\Gamma _{k}$
), where
$\Gamma _{k}$
), where
In particular, a uniformly n-convex function is a convex function. Note that (1.1) is elliptic for uniformly k-convex functions.
For
![]() $n\geq 3$
, consider the following problem:
$n\geq 3$
, consider the following problem:
 $$ \begin{align} \begin{cases} S_{k}(D^{2}u)=S_{l}(D^{2}u),&\mbox{in }{\mathbb R}^{n}\setminus\bar{B}_{1},\\ u=b,&\mbox{on }\partial B_{1},\\ u=\dfrac{\hat{a}}{2}|x|^{2}+c+O(|x|^{2-n}),&\mbox{as }|x|\rightarrow\infty, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} S_{k}(D^{2}u)=S_{l}(D^{2}u),&\mbox{in }{\mathbb R}^{n}\setminus\bar{B}_{1},\\ u=b,&\mbox{on }\partial B_{1},\\ u=\dfrac{\hat{a}}{2}|x|^{2}+c+O(|x|^{2-n}),&\mbox{as }|x|\rightarrow\infty, \end{cases} \end{align} $$
where
![]() $B_1$
denotes the unit ball in
$B_1$
denotes the unit ball in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
![]() $2\leq k\leq n$
,
$2\leq k\leq n$
,
![]() $0\leq l\leq k-1$
,
$0\leq l\leq k-1$
,
![]() $\hat {a}=(\binom {n}{l}/\binom {n}{k})^{\frac {1}{k-l}}$
, b,
$\hat {a}=(\binom {n}{l}/\binom {n}{k})^{\frac {1}{k-l}}$
, b,
![]() $c\in {\mathbb R}$
. Our first result can be stated as follows.
$c\in {\mathbb R}$
. Our first result can be stated as follows.
Theorem 1.1 For
![]() $n\geq 3$
, let
$n\geq 3$
, let
![]() $2\leq k\leq m\leq n, 1\leq l<k$
. Then problem (1.6) admits a unique radially symmetric uniformly m-convex solution
$2\leq k\leq m\leq n, 1\leq l<k$
. Then problem (1.6) admits a unique radially symmetric uniformly m-convex solution
if and only if
![]() $c\in [\mu (\alpha _{0}),\infty )$
for
$c\in [\mu (\alpha _{0}),\infty )$
for
![]() $m=k$
and
$m=k$
and
![]() $c\in [\mu (\alpha _{0}),\mu (\alpha _{m})]$
for
$c\in [\mu (\alpha _{0}),\mu (\alpha _{m})]$
for
![]() $k+1\leq m\leq n$
, where
$k+1\leq m\leq n$
, where
![]() $\xi (t)$
denotes the inverse function of
$\xi (t)$
denotes the inverse function of
in the interval
![]() $[a_{0},\infty )$
with
$[a_{0},\infty )$
with
 $$ \begin{align*}a_{0}=\bigg(\bigg(l\binom{n}{l}\bigg)/\bigg(k\binom{n}{k}\bigg)\bigg)^{\frac{1}{k-l}},\ \alpha_{0}=a_{0}^{l}\binom{n}{l}\frac{l-k}{k},\ \alpha_{m}=\bigg(\frac{(m-l)\binom{n}{l}}{(m-k)\binom{n}{k}}\bigg)^{\frac{l}{k-l}} \binom{n}{l}\frac{k-l}{m-k}\end{align*} $$
$$ \begin{align*}a_{0}=\bigg(\bigg(l\binom{n}{l}\bigg)/\bigg(k\binom{n}{k}\bigg)\bigg)^{\frac{1}{k-l}},\ \alpha_{0}=a_{0}^{l}\binom{n}{l}\frac{l-k}{k},\ \alpha_{m}=\bigg(\frac{(m-l)\binom{n}{l}}{(m-k)\binom{n}{k}}\bigg)^{\frac{l}{k-l}} \binom{n}{l}\frac{k-l}{m-k}\end{align*} $$
with
![]() $k+1\leq m\leq n$
and
$k+1\leq m\leq n$
and
Remark 1.2 For the case
![]() $l=0$
, the necessary and sufficient conditions on the existence of radially symmetric solutions of the exterior Dirichlet problem of Hessian equations were obtained by Wang and Bao [Reference Wang and Bao23].
$l=0$
, the necessary and sufficient conditions on the existence of radially symmetric solutions of the exterior Dirichlet problem of Hessian equations were obtained by Wang and Bao [Reference Wang and Bao23].
For
![]() $n=2$
, consider the following problem:
$n=2$
, consider the following problem:
 $$ \begin{align} \begin{cases} S_{2}(D^{2}u)=S_{1}(D^{2}u),&\mbox{in }\mathbb{R}^{n}\setminus\bar{B}_{1},\\ u=b,&\mbox{on }\partial B_{1},\\ u=|x|^{2}+\dfrac{\rho}{2}\ln|x|+c+O(|x|^{-2}),&\mbox{as }|x|\rightarrow\infty, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} S_{2}(D^{2}u)=S_{1}(D^{2}u),&\mbox{in }\mathbb{R}^{n}\setminus\bar{B}_{1},\\ u=b,&\mbox{on }\partial B_{1},\\ u=|x|^{2}+\dfrac{\rho}{2}\ln|x|+c+O(|x|^{-2}),&\mbox{as }|x|\rightarrow\infty, \end{cases} \end{align} $$
where b, c, and
![]() $\rho \in \mathbb {R}$
.
$\rho \in \mathbb {R}$
.
Theorem 1.3 For
![]() $n=2$
, problem (1.8) admits a unique radially symmetric convex solution
$n=2$
, problem (1.8) admits a unique radially symmetric convex solution
 $$ \begin{align} u(x)&=b-\dfrac{1}{2}+\dfrac{1}{2}|x|^2+\dfrac{1}{2}[|x|\sqrt{|x|^2+\rho}+\rho \ln(|x|+\sqrt{|x|^2+\rho})]\nonumber \\& \quad -\dfrac{1}{2}[\sqrt{1+\rho}+\rho \ln(1+\sqrt{1+\rho})] \end{align} $$
$$ \begin{align} u(x)&=b-\dfrac{1}{2}+\dfrac{1}{2}|x|^2+\dfrac{1}{2}[|x|\sqrt{|x|^2+\rho}+\rho \ln(|x|+\sqrt{|x|^2+\rho})]\nonumber \\& \quad -\dfrac{1}{2}[\sqrt{1+\rho}+\rho \ln(1+\sqrt{1+\rho})] \end{align} $$
if and only if
![]() $\rho \geq -1$
, and
$\rho \geq -1$
, and
![]() $c=\nu (\rho )$
, where
$c=\nu (\rho )$
, where
Corollary 1.4 For
![]() $n=2$
, problem (1.8) admits a unique radially symmetric convex solution (1.9) if and only if
$n=2$
, problem (1.8) admits a unique radially symmetric convex solution (1.9) if and only if
![]() $c\leq b-1.$
$c\leq b-1.$
In the second part of this paper, we obtain the existence of viscosity solutions of the exterior Dirichlet problem of the Hessian quotient equation (1.1) and (1.2).
Before stating our main result, we will first give the definition of viscosity solutions of (1.1) and (1.2).
Definition 1.5 A function
![]() $u\in C^0({\mathbb R}^{n}\setminus \Omega )$
is said to be a viscosity subsolution (supersolution) of (1.1) and (1.2), if
$u\in C^0({\mathbb R}^{n}\setminus \Omega )$
is said to be a viscosity subsolution (supersolution) of (1.1) and (1.2), if
![]() $u\leq \phi $
(
$u\leq \phi $
(
![]() $u\geq \phi $
) on
$u\geq \phi $
) on
![]() $\partial \Omega $
and for any
$\partial \Omega $
and for any
![]() $\bar {x}\in {\mathbb R}^{n}\setminus \bar {\Omega }$
and any uniformly k-convex function
$\bar {x}\in {\mathbb R}^{n}\setminus \bar {\Omega }$
and any uniformly k-convex function
![]() $v\in C^{2}({\mathbb R}^{n}\setminus \bar {\Omega })$
satisfying
$v\in C^{2}({\mathbb R}^{n}\setminus \bar {\Omega })$
satisfying
we have
 $$ \begin{align*}\frac{S_{k}(D^{2} v(\bar{x}))}{S_{l}(D^{2} v(\bar{x}))}\geq (\leq)~g(\bar{x}).\end{align*} $$
$$ \begin{align*}\frac{S_{k}(D^{2} v(\bar{x}))}{S_{l}(D^{2} v(\bar{x}))}\geq (\leq)~g(\bar{x}).\end{align*} $$
If
![]() $u\in C^{0}({\mathbb R}^{n}\setminus \Omega )$
is both a viscosity subsolution and a viscosity supersolution of (1.1) and (1.2), we say that u is a viscosity solution of (1.1) and (1.2).
$u\in C^{0}({\mathbb R}^{n}\setminus \Omega )$
is both a viscosity subsolution and a viscosity supersolution of (1.1) and (1.2), we say that u is a viscosity solution of (1.1) and (1.2).
Suppose that
![]() $g\in C^0(\mathbb {R}^n)$
satisfies
$g\in C^0(\mathbb {R}^n)$
satisfies
and for some constant
![]() $\beta>2$
,
$\beta>2$
,
where
and
![]() $g_0\in C^{0}([0,+\infty ))$
satisfies
$g_0\in C^{0}([0,+\infty ))$
satisfies
and
Our main result can be stated as follows.
Theorem 1.6 For
![]() $n\geq 3$
, let
$n\geq 3$
, let
![]() $0\leq l<k\leq n$
and
$0\leq l<k\leq n$
and
![]() $\frac {k-l}{\overline {t}_k-\underline {t}_l}>2$
. Assume that g satisfies (1.10) and (1.11). Then, for any given
$\frac {k-l}{\overline {t}_k-\underline {t}_l}>2$
. Assume that g satisfies (1.10) and (1.11). Then, for any given
![]() $b\in \mathbb {R}^{n}$
and
$b\in \mathbb {R}^{n}$
and
![]() $A\in \mathcal {A}_{k,l}$
, there exists some constant
$A\in \mathcal {A}_{k,l}$
, there exists some constant
![]() $\tilde {c}$
, depending only on
$\tilde {c}$
, depending only on
![]() $n,~b,~A,~\Omega ,~g,~g_0$
,
$n,~b,~A,~\Omega ,~g,~g_0$
,
![]() $||\phi ||_{C^{2}(\partial \Omega )}$
, such that for every
$||\phi ||_{C^{2}(\partial \Omega )}$
, such that for every
![]() $c>\tilde {c}$
, there exists a unique viscosity solution
$c>\tilde {c}$
, there exists a unique viscosity solution
![]() $u\in C^{0}(\mathbb {R}^{n}\backslash \Omega )$
of (1.1) and (1.2) with the following prescribed asymptotic behavior at infinity:
$u\in C^{0}(\mathbb {R}^{n}\backslash \Omega )$
of (1.1) and (1.2) with the following prescribed asymptotic behavior at infinity:
 $$ \begin{align} u(x)=u_0(x)+b\cdot x+c+O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \ \mbox{as}\ \ |x|\to\infty,\ \mbox{if}\ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{align} $$
$$ \begin{align} u(x)=u_0(x)+b\cdot x+c+O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \ \mbox{as}\ \ |x|\to\infty,\ \mbox{if}\ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{align} $$
or
 $$ \begin{align} u(x)=u_0(x)+b\cdot x+c+O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}\ln |x|),\ \ \mbox{as}\ \ |x|\to\infty,\ \mbox{if}\ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{align} $$
$$ \begin{align} u(x)=u_0(x)+b\cdot x+c+O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}\ln |x|),\ \ \mbox{as}\ \ |x|\to\infty,\ \mbox{if}\ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{align} $$
where
![]() $u_0(x)=\int _{0}^{r_A(x)}\theta h_0(\theta )d\theta $
with
$u_0(x)=\int _{0}^{r_A(x)}\theta h_0(\theta )d\theta $
with
![]() $h_{0}$
satisfying
$h_{0}$
satisfying
 $$ \begin{align} \begin{cases} \dfrac{h_0(r)^k+\overline{t}_k r h_0(r)^{k-1}h_0^{\prime}(r)}{h_0(r)^l+\underline{t}_l r h_0(r)^{l-1}h_0^{\prime}(r)}=g_0(r),\ r>0,\\\\[-12pt] h_0(0)>\sup_{r\in [0,+\infty)} g_0^{\frac{1}{k-l}}(r),\\ h_0(r)^k+\overline{t}_k r h_0(r)^{k-1}h_0^{\prime}(r)>0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \dfrac{h_0(r)^k+\overline{t}_k r h_0(r)^{k-1}h_0^{\prime}(r)}{h_0(r)^l+\underline{t}_l r h_0(r)^{l-1}h_0^{\prime}(r)}=g_0(r),\ r>0,\\\\[-12pt] h_0(0)>\sup_{r\in [0,+\infty)} g_0^{\frac{1}{k-l}}(r),\\ h_0(r)^k+\overline{t}_k r h_0(r)^{k-1}h_0^{\prime}(r)>0. \end{cases} \end{align} $$
Remark 1.7 Under the assumption of
![]() $g_{0}$
, by the classical existence, uniqueness and extension theorem for the solution of the initial value problem of the ODE, we know that (1.15) admits a bounded solution
$g_{0}$
, by the classical existence, uniqueness and extension theorem for the solution of the initial value problem of the ODE, we know that (1.15) admits a bounded solution
![]() $h_0$
in
$h_0$
in
![]() $C^0[0,+\infty )\cap C^1(0,+\infty )$
. In particular, if
$C^0[0,+\infty )\cap C^1(0,+\infty )$
. In particular, if
![]() $g_{0}\equiv 1$
, then
$g_{0}\equiv 1$
, then
![]() $h_0\equiv 1$
and
$h_0\equiv 1$
and
![]() $u_0(x)=\frac {1}{2}x^{T}Ax$
.
$u_0(x)=\frac {1}{2}x^{T}Ax$
.
The rest of this paper is organized as follows. In Section 2, we will prove Theorems 1.1 and 1.2. In Section 3, we will construct a family of generalized symmetric smooth k-convex subsolutions and supersolutions of (1.1) by analyzing the corresponding ODE. In Section 4, we will finish the proof of Theorem 1.6 by Perron’s method. In Appendix A, we will give the Appendix.
2 Proof of Theorems 1.1 and 1.3
Before proving Theorems 1.1 and 1.3, we will first make some preliminaries.
Consider the function
It is easy to see that t is smooth and strictly increasing on the interval
![]() $[a_{0},\infty )$
. Let
$[a_{0},\infty )$
. Let
![]() $\xi =\xi (t)$
denote the inverse function of t on the interval
$\xi =\xi (t)$
denote the inverse function of t on the interval
![]() $[a_{0},\infty )$
. Then
$[a_{0},\infty )$
. Then
![]() $\xi $
is smooth and strictly increasing on
$\xi $
is smooth and strictly increasing on
![]() $[\alpha _{0},\infty )$
. Moreover,
$[\alpha _{0},\infty )$
. Moreover,
Let
![]() $\mu (\alpha )$
be defined as in (1.7). Then
$\mu (\alpha )$
be defined as in (1.7). Then
![]() $\mu $
has the following properties.
$\mu $
has the following properties.
Lemma 2.1
![]() $\mu $
is smooth, strictly increasing on
$\mu $
is smooth, strictly increasing on
![]() $[\alpha _{0},\infty )$
and
$[\alpha _{0},\infty )$
and
![]() $\lim \limits _{\alpha \rightarrow \infty }\mu (\alpha )=\infty $
.
$\lim \limits _{\alpha \rightarrow \infty }\mu (\alpha )=\infty $
.
Proof The smoothness of
![]() $\mu $
follows directly from the smoothness of
$\mu $
follows directly from the smoothness of
![]() $\xi $
. Then, by a direct computation,
$\xi $
. Then, by a direct computation,
Therefore, Lemma 2.1 follows directly from the facts that
![]() $\xi (t)$
is strictly increasing on
$\xi (t)$
is strictly increasing on
![]() $[\alpha _{0},\infty )$
and
$[\alpha _{0},\infty )$
and
![]() $\lim \limits _{t\rightarrow \infty }\xi (t)=\infty $
.
$\lim \limits _{t\rightarrow \infty }\xi (t)=\infty $
.
Lemma 2.2 Let
![]() $2\leq k\leq m\leq n$
and
$2\leq k\leq m\leq n$
and
![]() $0\leq l\leq k-1$
. Assume that
$0\leq l\leq k-1$
. Assume that
![]() $\lambda =(\beta ,\gamma ,\dots ,\gamma )\in {\mathbb R}^{n}$
and
$\lambda =(\beta ,\gamma ,\dots ,\gamma )\in {\mathbb R}^{n}$
and
![]() $\sigma _{k}(\lambda )=\sigma _{l}(\lambda )$
. Then
$\sigma _{k}(\lambda )=\sigma _{l}(\lambda )$
. Then
![]() $\lambda \in \Gamma _{m}$
if and only if
$\lambda \in \Gamma _{m}$
if and only if
where
 $$ \begin{align*} \gamma_{m}=\begin{cases} \left(\frac{(m-l)\binom{n}{l}}{(m-k)\binom{n}{k}}\right)^{\frac{1}{k-l}},&k+1\leq m\leq n,\\ \infty,&m=k. \end{cases} \end{align*} $$
$$ \begin{align*} \gamma_{m}=\begin{cases} \left(\frac{(m-l)\binom{n}{l}}{(m-k)\binom{n}{k}}\right)^{\frac{1}{k-l}},&k+1\leq m\leq n,\\ \infty,&m=k. \end{cases} \end{align*} $$
Proof If
![]() $\lambda \in \Gamma _{m}$
, we have that for
$\lambda \in \Gamma _{m}$
, we have that for
![]() $j=1$
,
$j=1$
,
![]() $\dots $
, m,
$\dots $
, m,
which implies that
By [Reference Wang and Bao23, Lemma 1], we have that
![]() $\gamma>0$
. It follows that
$\gamma>0$
. It follows that
for
![]() $j=1$
,
$j=1$
,
![]() $\dots $
, m.
$\dots $
, m.
The equation
![]() $\sigma _{k}(\lambda )=\sigma _{l}(\lambda )$
can be equivalently written as
$\sigma _{k}(\lambda )=\sigma _{l}(\lambda )$
can be equivalently written as
Since
![]() $\gamma>0$
, dividing the above equality by
$\gamma>0$
, dividing the above equality by
![]() $\gamma ^{l-1}$
, we have that
$\gamma ^{l-1}$
, we have that
 $$ \begin{align} \bigg[k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}\bigg]\beta=\gamma\bigg[(n-l)\binom{n}{l}-(n-k)\binom{n}{k}\gamma^{k-l}\bigg]. \end{align} $$
$$ \begin{align} \bigg[k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}\bigg]\beta=\gamma\bigg[(n-l)\binom{n}{l}-(n-k)\binom{n}{k}\gamma^{k-l}\bigg]. \end{align} $$
It is easy to see that
![]() $\gamma \neq a_{0}$
. Indeed, if
$\gamma \neq a_{0}$
. Indeed, if
![]() $\gamma =a_{0}$
, then the left-hand side of (2.2) equals to
$\gamma =a_{0}$
, then the left-hand side of (2.2) equals to
![]() $0$
. However, the right-hand side of (2.2) equals
$0$
. However, the right-hand side of (2.2) equals
![]() $a_{0}^{l}\binom {n}{l}\frac {n(k-l)}{k}\neq 0$
, which is a contradiction.
$a_{0}^{l}\binom {n}{l}\frac {n(k-l)}{k}\neq 0$
, which is a contradiction.
It follows from (2.2) and
![]() $\gamma \neq a_{0}$
that
$\gamma \neq a_{0}$
that
 $$ \begin{align} \beta=\frac{(n-l)\binom{n}{l}-(n-k)\binom{n}{k}\gamma^{k-l}}{k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}}\gamma. \end{align} $$
$$ \begin{align} \beta=\frac{(n-l)\binom{n}{l}-(n-k)\binom{n}{k}\gamma^{k-l}}{k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}}\gamma. \end{align} $$
Inserting the above equality into (2.1), we have that
 $$ \begin{align} \frac{\binom{n}{k}(k-j)\gamma^{k-l}+\binom{n}{l}(j-l)}{k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}}>0, \end{align} $$
$$ \begin{align} \frac{\binom{n}{k}(k-j)\gamma^{k-l}+\binom{n}{l}(j-l)}{k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}}>0, \end{align} $$
for
![]() $j=1$
,
$j=1$
,
![]() $\dots $
, m.
$\dots $
, m.
Now we claim that
![]() $k\binom {n}{k}\gamma ^{k-l}-l\binom {n}{l}>0$
or equivalently,
$k\binom {n}{k}\gamma ^{k-l}-l\binom {n}{l}>0$
or equivalently,
![]() $\gamma>a_{0}$
. Indeed, if
$\gamma>a_{0}$
. Indeed, if
![]() $k\binom {n}{k}\gamma ^{k-l}-l\binom {n}{l}<0$
, on one hand, we have that by (2.4)
$k\binom {n}{k}\gamma ^{k-l}-l\binom {n}{l}<0$
, on one hand, we have that by (2.4)
On the other hand,
for any
![]() $l+1\leq j\leq k$
, which is a contradiction.
$l+1\leq j\leq k$
, which is a contradiction.
For
![]() $m=k$
, we have already obtained that
$m=k$
, we have already obtained that
![]() $a_{0}<\gamma <\infty $
. For
$a_{0}<\gamma <\infty $
. For
![]() $k+1\leq m\leq n$
, by
$k+1\leq m\leq n$
, by
![]() $\gamma>a_{0}$
and (2.4), we have that
$\gamma>a_{0}$
and (2.4), we have that
 $$ \begin{align*} \gamma^{k-l}<\frac{\binom{n}{l}(j-l)}{\binom{n}{k}(j-k)},~~~~\forall~j=k+1,\dots,m. \end{align*} $$
$$ \begin{align*} \gamma^{k-l}<\frac{\binom{n}{l}(j-l)}{\binom{n}{k}(j-k)},~~~~\forall~j=k+1,\dots,m. \end{align*} $$
Then we can conclude that
![]() $a_{0}<\gamma <\gamma _{m}$
.
$a_{0}<\gamma <\gamma _{m}$
.
Conversely, if
![]() $a_{0}<\gamma <\gamma _{m}$
, it is easy to check that
$a_{0}<\gamma <\gamma _{m}$
, it is easy to check that
![]() $\lambda \in \Gamma _{m}$
. Indeed, by (2.3), we have that for
$\lambda \in \Gamma _{m}$
. Indeed, by (2.3), we have that for
![]() $j=1$
,
$j=1$
,
![]() $\dots $
, m,
$\dots $
, m,
 $$ \begin{align*} j\beta+(n-j)\gamma=\frac{\binom{n}{k}(k-j)\gamma^{k-l}+\binom{n}{l}(j-l)}{k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}}>0. \end{align*} $$
$$ \begin{align*} j\beta+(n-j)\gamma=\frac{\binom{n}{k}(k-j)\gamma^{k-l}+\binom{n}{l}(j-l)}{k\binom{n}{k}\gamma^{k-l}-l\binom{n}{l}}>0. \end{align*} $$
It follows from the above inequality and
![]() $\gamma>0$
that
$\gamma>0$
that
Lemma 2.2 is proved.
Proof of Theorem 1.1
If
![]() $c\in [\mu (\alpha _{0}),\infty )$
for
$c\in [\mu (\alpha _{0}),\infty )$
for
![]() $m=k$
or
$m=k$
or
![]() $c\in [\mu (\alpha _{0}),\mu (\alpha _{m})]$
for
$c\in [\mu (\alpha _{0}),\mu (\alpha _{m})]$
for
![]() $k+1\leq m\leq n$
, by the intermediate value theorem and Lemma 2.1, there exists uniquely
$k+1\leq m\leq n$
, by the intermediate value theorem and Lemma 2.1, there exists uniquely
![]() $\alpha _{0}\leq \alpha <\infty $
for
$\alpha _{0}\leq \alpha <\infty $
for
![]() $m=k$
or
$m=k$
or
![]() $\alpha _{0}\leq \alpha \leq \alpha _{m}$
for
$\alpha _{0}\leq \alpha \leq \alpha _{m}$
for
![]() $k+1\leq m\leq n$
such that
$k+1\leq m\leq n$
such that
![]() $c=\mu (\alpha )$
. Consider the function
$c=\mu (\alpha )$
. Consider the function
Here and throughout of this section, we use r to denote
![]() $r_{I}$
defined as in (1.12).
$r_{I}$
defined as in (1.12).
Next, we shall prove that u is the unique uniformly m-convex solution to (1.6). The uniqueness of u follows directly from the comparison principle (see [Reference Li, Nguyen and Wang20, Theorem 1.7]). It is obvious that u satisfies the second line in (1.6) by taking
![]() $r=1$
in (2.5). Differentiating (2.5) with respect to
$r=1$
in (2.5). Differentiating (2.5) with respect to
![]() $r>1$
, it follows from the range of
$r>1$
, it follows from the range of
![]() $\alpha $
and the monotonicity of
$\alpha $
and the monotonicity of
![]() $\xi $
that
$\xi $
that
By (2.6) and Lemma 2.2, we can conclude that u is uniformly m-convex. Since
![]() $\xi (t)$
is the inverse function of
$\xi (t)$
is the inverse function of
![]() $t=\binom {n}{k}\xi ^{k}-\binom {n}{l}\xi ^{l}$
on the interval
$t=\binom {n}{k}\xi ^{k}-\binom {n}{l}\xi ^{l}$
on the interval
![]() $[a_{0},\infty )$
, then equation (2.6) can be equivalently written as
$[a_{0},\infty )$
, then equation (2.6) can be equivalently written as
 $$ \begin{align} \alpha r^{-n}&=\binom{n}{k}\xi^{k}(\alpha r^{-n})-\binom{n}{l}\xi^{l}(\alpha r^{-n})\nonumber\\ &=\binom{n}{k}(\frac{u'}{r})^{k}-\binom{n}{l}(\frac{u'}{r})^{l},~~~~\forall~r>1. \end{align} $$
$$ \begin{align} \alpha r^{-n}&=\binom{n}{k}\xi^{k}(\alpha r^{-n})-\binom{n}{l}\xi^{l}(\alpha r^{-n})\nonumber\\ &=\binom{n}{k}(\frac{u'}{r})^{k}-\binom{n}{l}(\frac{u'}{r})^{l},~~~~\forall~r>1. \end{align} $$
By differentiating (2.7) with respect to r, we have that u satisfies the first line in (1.6). It only remains to prove that u satisfies the third line in (1.6). Since
 $$ \begin{align*} \xi(t)&=\xi(0)+\xi'(0)t+O(t^{2})\\ &=\hat{a}+\frac{t}{(k-l)\hat{a}^{l-1}\binom{n}{l}}+O(t^{2}), \end{align*} $$
$$ \begin{align*} \xi(t)&=\xi(0)+\xi'(0)t+O(t^{2})\\ &=\hat{a}+\frac{t}{(k-l)\hat{a}^{l-1}\binom{n}{l}}+O(t^{2}), \end{align*} $$
as
![]() $t\rightarrow 0$
, then we have that
$t\rightarrow 0$
, then we have that
 $$ \begin{align} u(r)&=\frac{\hat{a}^{2}}{2}r^{2}+b-\frac{\hat{a}}{2}+\int_{1}^{r}s[\xi(\alpha s^{-n})-\hat{a}]ds\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+b-\frac{\hat{a}}{2}+\int_{1}^{\infty}s[\xi(\alpha s^{-n})-\hat{a}]ds-\int_{r}^{\infty}s[\xi(\alpha s^{-n})-\hat{a}]ds\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+\mu(\alpha)-\int_{r}^{\infty}s[\xi(\alpha s^{-n})-\hat{a}]ds\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+\mu(\alpha)+O(r^{2-n})\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+c+O(r^{2-n}), \end{align} $$
$$ \begin{align} u(r)&=\frac{\hat{a}^{2}}{2}r^{2}+b-\frac{\hat{a}}{2}+\int_{1}^{r}s[\xi(\alpha s^{-n})-\hat{a}]ds\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+b-\frac{\hat{a}}{2}+\int_{1}^{\infty}s[\xi(\alpha s^{-n})-\hat{a}]ds-\int_{r}^{\infty}s[\xi(\alpha s^{-n})-\hat{a}]ds\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+\mu(\alpha)-\int_{r}^{\infty}s[\xi(\alpha s^{-n})-\hat{a}]ds\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+\mu(\alpha)+O(r^{2-n})\nonumber\\ &=\frac{\hat{a}^{2}}{2}r^{2}+c+O(r^{2-n}), \end{align} $$
as
![]() $r\rightarrow \infty $
.
$r\rightarrow \infty $
.
Conversely, suppose that u is the unique radially symmetric uniformly m-convex solution to (1.6). By Lemma 2.2, we have that
The first line in (1.6) can be written as
By multiplying the above equation by
![]() $r^{n-1}$
, we have that
$r^{n-1}$
, we have that
Then there exists
![]() $\alpha \in {\mathbb R}$
such that
$\alpha \in {\mathbb R}$
such that
By (2.9), (2.10), and the monotonicity of
![]() $t=\binom {n}{k}\xi ^{k}-\binom {n}{l}\xi ^{l}$
, we can conclude that
$t=\binom {n}{k}\xi ^{k}-\binom {n}{l}\xi ^{l}$
, we can conclude that
![]() $\alpha _{0}\leq \alpha <\infty $
for
$\alpha _{0}\leq \alpha <\infty $
for
![]() $m=k$
and
$m=k$
and
![]() $\alpha _{0}\leq \alpha \leq \alpha _{m}$
for
$\alpha _{0}\leq \alpha \leq \alpha _{m}$
for
![]() $k+1\leq m\leq n$
. By the definition of
$k+1\leq m\leq n$
. By the definition of
![]() $\xi $
, we can solve
$\xi $
, we can solve
![]() $u'/r$
from (2.10), that is,
$u'/r$
from (2.10), that is,
It follows that
Then, by (2.8) and Lemma 2.2,
![]() $c=\mu (\alpha )\in [\mu (\alpha _{0}),\mu (\alpha _{1})]$
.
$c=\mu (\alpha )\in [\mu (\alpha _{0}),\mu (\alpha _{1})]$
.
Theorem 1.1 is proved.
Proof of Theorem 1.3
If
![]() $\rho \geq -1$
and
$\rho \geq -1$
and
![]() $c=\nu (\rho )$
, we will prove that u defined as in (1.9) is the unique convex solution to (1.8) as follows.
$c=\nu (\rho )$
, we will prove that u defined as in (1.9) is the unique convex solution to (1.8) as follows.
The uniqueness of u follows directly from the comparison principle (see [Reference Li, Nguyen and Wang20, Theorem 1.7]). It is obvious that u satisfies the second line in (1.8) by taking
![]() $r=1$
in (1.9). Differentiating (1.9) with respect to
$r=1$
in (1.9). Differentiating (1.9) with respect to
![]() $r>1$
, we have that
$r>1$
, we have that
 $$ \begin{align} \frac{u'(r)}{r}=1+\frac{\sqrt{r^{2}+\rho}}{r}>1,~~~~\forall~r>1. \end{align} $$
$$ \begin{align} \frac{u'(r)}{r}=1+\frac{\sqrt{r^{2}+\rho}}{r}>1,~~~~\forall~r>1. \end{align} $$
By applying Lemma 2.2 with
![]() $n=m=k=2$
and
$n=m=k=2$
and
![]() $l=1$
, we have that u is convex. By a direct computation,
$l=1$
, we have that u is convex. By a direct computation,
 $$ \begin{align*} &S_{2}(D^{2}u)-S_{1}(D^{2}u)\\ & \quad =u"\frac{u'}{r}-(u"+\frac{u'}{r})\\ & \quad =0, \end{align*} $$
$$ \begin{align*} &S_{2}(D^{2}u)-S_{1}(D^{2}u)\\ & \quad =u"\frac{u'}{r}-(u"+\frac{u'}{r})\\ & \quad =0, \end{align*} $$
which implies that u satisfies the first line in (1.8). It only remains to prove that u satisfies the third line in (1.8). Since
and
as
![]() $r\rightarrow \infty $
, we have that
$r\rightarrow \infty $
, we have that
as
![]() $r\rightarrow \infty $
, which implies that u satisfies the third line in (1.8).
$r\rightarrow \infty $
, which implies that u satisfies the third line in (1.8).
Conversely, suppose that u is the unique radially symmetric convex solution to (1.8). The first line in (1.8) can be written as
By multiplying the above equation by
![]() $2r$
, we have that
$2r$
, we have that
Then there exists
![]() $\rho \in {\mathbb R}$
such that
$\rho \in {\mathbb R}$
such that
It follows that
which implies that
![]() $\rho \geq -1$
. By Lemma 2.2 with
$\rho \geq -1$
. By Lemma 2.2 with
![]() $n=m=k=2$
and
$n=m=k=2$
and
![]() $l=1$
, we have that
$l=1$
, we have that
Combining (2.13) and (2.14), we can solve
![]() $u'$
as
$u'$
as
Integrating the above equality from
![]() $1$
to r, we have that u must take the form as in (1.9). Moreover, by expanding u at infinity as in (2.12), we can conclude that
$1$
to r, we have that u must take the form as in (1.9). Moreover, by expanding u at infinity as in (2.12), we can conclude that
![]() $c=\nu (\rho )$
.
$c=\nu (\rho )$
.
Theorem 1.3 is proved.
Proof of Corollary 1.4
By the argument in [Reference Wang and Bao23], we have that
![]() $\nu (\rho )$
is increasing on
$\nu (\rho )$
is increasing on
![]() $[-1,0]$
and decreasing on
$[-1,0]$
and decreasing on
![]() $[0,\infty )$
. Thus,
$[0,\infty )$
. Thus,
Then Corollary 1.4 follows from the above inequality and Theorem 1.3.
Remark 2.3 If
![]() $k=n=2,l=0,$
we can refer to Theorem 2 in [Reference Wang and Bao23].
$k=n=2,l=0,$
we can refer to Theorem 2 in [Reference Wang and Bao23].
3 Generalized symmetric functions, subsolutions and supersolutions
In this section, we will construct a family of generalized symmetric smooth subsolutions and supersolutions of (1.1).
For any
![]() $A\in \mathcal {A}_{k,l}$
, without loss of generality, we may assume that A is diagonal, that is,
$A\in \mathcal {A}_{k,l}$
, without loss of generality, we may assume that A is diagonal, that is,
where
![]() $a=(a_{1},\dots ,a_{n})\in \mathbb {R}^n$
and
$a=(a_{1},\dots ,a_{n})\in \mathbb {R}^n$
and
![]() $0<a_1\leq a_2\leq \dots \leq a_n$
.
$0<a_1\leq a_2\leq \dots \leq a_n$
.
Definition 3.1 A function u is called a generalized symmetric function with respect to A if u is of the form
 $$ \begin{align*} u(x)=u(r)=u(r_A(x))=u((\sum \limits_{i=1}^{n}a_{i}x_{i}^{2})^{\frac{1}{2}}), \end{align*} $$
$$ \begin{align*} u(x)=u(r)=u(r_A(x))=u((\sum \limits_{i=1}^{n}a_{i}x_{i}^{2})^{\frac{1}{2}}), \end{align*} $$
where
![]() $r:=r_{A}(x)$
is defined as in (1.12).
$r:=r_{A}(x)$
is defined as in (1.12).
If u is both a generalized symmetric function with respect to A and a subsolution (supersolution, solution) of (1.1), then we say that u is a generalized symmetric subsolution (supersolution, solution) of (1.1).
By the assumptions on g, there exist functions
![]() $\overline {g},\underline {g}\in C^{0}([0,+\infty ))$
satisfying
$\overline {g},\underline {g}\in C^{0}([0,+\infty ))$
satisfying
and
Moreover,
![]() $\underline {g}(r)$
is strictly increasing in r and for some
$\underline {g}(r)$
is strictly increasing in r and for some
![]() $C_{1}$
,
$C_{1}$
,
![]() $\theta _{0}>0$
, we have that
$\theta _{0}>0$
, we have that
and
In order to construct the subsolutions of (1.1), we want to construct the generalized symmetric subsolutions or solutions of
 $$ \begin{align} \frac{S_{k}(D^{2}v)}{S_{l}(D^{2}v)}=\overline{g}(r). \end{align} $$
$$ \begin{align} \frac{S_{k}(D^{2}v)}{S_{l}(D^{2}v)}=\overline{g}(r). \end{align} $$
However, Proposition A.1 tells us that it is impossible to construct the generalized symmetric solutions of the above equation for
![]() $1\leq k\leq n-1$
directly unless
$1\leq k\leq n-1$
directly unless
![]() $A=\hat {a}I$
.
$A=\hat {a}I$
.
Thus, we will construct the generalized symmetric smooth subsolutions of (3.3). Indeed, we will construct the subsolutions of the form
where
![]() $\beta _{1}\in {\mathbb R}$
,
$\beta _{1}\in {\mathbb R}$
,
![]() $\eta>1$
,
$\eta>1$
,
![]() $\delta>\sup _{r\in [1,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
, and
$\delta>\sup _{r\in [1,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
, and
![]() $h=h(\theta ,\delta )$
is obtained as follows.
$h=h(\theta ,\delta )$
is obtained as follows.
Lemma 3.2 For
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $0\leq l<k\leq n$
, the following problem
$0\leq l<k\leq n$
, the following problem
 $$ \begin{align} \begin{cases} \dfrac{h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r)}{h(r)^l+\underline{t}_l r h(r)^{l-1}h'(r)}=\overline{g}(r),\ r>1,\\ h(1)=\delta,\\ h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r)>0 \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \dfrac{h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r)}{h(r)^l+\underline{t}_l r h(r)^{l-1}h'(r)}=\overline{g}(r),\ r>1,\\ h(1)=\delta,\\ h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r)>0 \end{cases} \end{align} $$
admits a smooth solution
![]() $h=h(r,\delta )$
on
$h=h(r,\delta )$
on
![]() $[1,+\infty )$
satisfying:
$[1,+\infty )$
satisfying:
-
(i)
 $\overline {g}^{\frac {1}{k-l}}(r)\leq h(r,\delta )\leq \delta ,$
and
$\overline {g}^{\frac {1}{k-l}}(r)\leq h(r,\delta )\leq \delta ,$
and
 $\partial _{r}h(r,\delta )\leq 0$
.
$\partial _{r}h(r,\delta )\leq 0$
. -
(ii)
 $h(r,\delta )$
is continuous and strictly increasing in
$h(r,\delta )$
is continuous and strictly increasing in
 $\delta $
and
$\delta $
and  $$ \begin{align*}\lim_{\delta\to+\infty}h(r,\delta)=+\infty,\ \forall\ r\geq 1.\end{align*} $$
$$ \begin{align*}\lim_{\delta\to+\infty}h(r,\delta)=+\infty,\ \forall\ r\geq 1.\end{align*} $$
Proof For brevity, sometimes we write
![]() $h(r)$
or
$h(r)$
or
![]() $h(r,\delta )$
,
$h(r,\delta )$
,
![]() $\overline {t}_k(a)$
or
$\overline {t}_k(a)$
or
![]() $\overline {t}_k$
and
$\overline {t}_k$
and
![]() $\underline {t}_l(a)$
or
$\underline {t}_l(a)$
or
![]() $\underline {t}_l$
, when there is no confusion. By (3.4), we have that
$\underline {t}_l$
, when there is no confusion. By (3.4), we have that
 $$ \begin{align} \begin{cases} \displaystyle\frac{\mbox{d} h}{\mbox{d}r}=-\frac{1}{r}\dfrac{h}{\overline{t}_k}\dfrac{h(r)^{k-l}- \overline{g}(r)}{h(r)^{k-l}-\overline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}=:V(h,r),\ r>1,\\ h(1)=\delta. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \displaystyle\frac{\mbox{d} h}{\mbox{d}r}=-\frac{1}{r}\dfrac{h}{\overline{t}_k}\dfrac{h(r)^{k-l}- \overline{g}(r)}{h(r)^{k-l}-\overline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}=:V(h,r),\ r>1,\\ h(1)=\delta. \end{cases} \end{align} $$
Then
![]() $\partial V/\partial h$
is continuous and V satisfies the local Lipschitz condition in the domain
$\partial V/\partial h$
is continuous and V satisfies the local Lipschitz condition in the domain
![]() $(\overline {g}^{\frac {1}{k-l}}(r),\delta )\times (1,+\infty )$
. Since
$(\overline {g}^{\frac {1}{k-l}}(r),\delta )\times (1,+\infty )$
. Since
![]() $\delta> \sup _{r\in [0,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
and
$\delta> \sup _{r\in [0,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
and
![]() $\underline {t}_l/\overline {t}_k<1$
, so by the existence, uniqueness, and extension theorem for the solution of the initial value problem of the ODE, we obtain that problem (3.4) has a smooth solution
$\underline {t}_l/\overline {t}_k<1$
, so by the existence, uniqueness, and extension theorem for the solution of the initial value problem of the ODE, we obtain that problem (3.4) has a smooth solution
![]() $h(r,\delta )$
such that
$h(r,\delta )$
such that
![]() $\overline {g}^{\frac {1}{k-l}}(r)\leq h(r,\delta )\leq \delta ,$
and
$\overline {g}^{\frac {1}{k-l}}(r)\leq h(r,\delta )\leq \delta ,$
and
![]() $\partial _{r}h(r,\delta )\leq 0$
. Then assertion (i) of this lemma is proved.
$\partial _{r}h(r,\delta )\leq 0$
. Then assertion (i) of this lemma is proved.
By (3.4), we have that
 $$ \begin{align*}\dfrac{(r^{\frac{k}{\overline{t}_k}}h^{k}(r))^{\prime}}{(r^{\frac{l}{\underline{t}_l}}h^{l}(r))^{\prime}}=\dfrac{\frac{k}{\overline{t}_k}r^{\frac{k}{\overline{t}_k}-1}(h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r))}{\frac{l}{\underline{t}_l}r^{\frac{l}{\underline{t}_l}-1}(h(r)^l+\underline{t}_l r h(r)^{l-1}h'(r))}=\dfrac{\frac{k}{\overline{t}_k}r^{\frac{k}{\overline{t}_k}-1}}{\frac{l}{\underline{t}_l}r^{\frac{l}{\underline{t}_l}-1}}\overline{g}(r),\ r>1,\end{align*} $$
$$ \begin{align*}\dfrac{(r^{\frac{k}{\overline{t}_k}}h^{k}(r))^{\prime}}{(r^{\frac{l}{\underline{t}_l}}h^{l}(r))^{\prime}}=\dfrac{\frac{k}{\overline{t}_k}r^{\frac{k}{\overline{t}_k}-1}(h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r))}{\frac{l}{\underline{t}_l}r^{\frac{l}{\underline{t}_l}-1}(h(r)^l+\underline{t}_l r h(r)^{l-1}h'(r))}=\dfrac{\frac{k}{\overline{t}_k}r^{\frac{k}{\overline{t}_k}-1}}{\frac{l}{\underline{t}_l}r^{\frac{l}{\underline{t}_l}-1}}\overline{g}(r),\ r>1,\end{align*} $$
that is,
Integrating the above equality from
![]() $1$
to r, we have that
$1$
to r, we have that
Then
Since
![]() $h(r)^k+\overline {t}_k r h(r)^{k-1}h'(r)>0$
, then
$h(r)^k+\overline {t}_k r h(r)^{k-1}h'(r)>0$
, then
![]() $h(r)^l+\underline {t}_l r h(r)^{l-1}h'(r)>0$
, so also
$h(r)^l+\underline {t}_l r h(r)^{l-1}h'(r)>0$
, so also
![]() $(r^{\frac {l}{\underline {t}_l}}h^{l}(r))^{\prime }>0.$
According to the mean value theorem of integrals, we have that there exists
$(r^{\frac {l}{\underline {t}_l}}h^{l}(r))^{\prime }>0.$
According to the mean value theorem of integrals, we have that there exists
![]() $1\leq \theta _1\leq r$
such that
$1\leq \theta _1\leq r$
such that
 $$ \begin{align*}r^{\frac{k}{\overline{t}_k}}h^{k}(r)-\delta^k =\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\displaystyle\int_1^r(s^{\frac{l}{\underline{t}_l}}h^{l}(s))^{\prime}ds,\end{align*} $$
$$ \begin{align*}r^{\frac{k}{\overline{t}_k}}h^{k}(r)-\delta^k =\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\displaystyle\int_1^r(s^{\frac{l}{\underline{t}_l}}h^{l}(s))^{\prime}ds,\end{align*} $$
i.e.,
 $$ \begin{align}F(h,\delta,\theta_1,r):=r^{\frac{k}{\overline{t}_k}}h^{k}(r)-\delta^k -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r) +\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\delta^l=0.\end{align} $$
$$ \begin{align}F(h,\delta,\theta_1,r):=r^{\frac{k}{\overline{t}_k}}h^{k}(r)-\delta^k -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r) +\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\delta^l=0.\end{align} $$
Then we claim that
 $$ \begin{align}\dfrac{\partial F}{\partial h} =k\left[r^{\frac{k}{\overline{t}_k}}h^{k-1} -\dfrac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l-1}\right]>0.\end{align} $$
$$ \begin{align}\dfrac{\partial F}{\partial h} =k\left[r^{\frac{k}{\overline{t}_k}}h^{k-1} -\dfrac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l-1}\right]>0.\end{align} $$
Indeed, by (3.7), we have that
 $$ \begin{align}r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r) =\delta^l\left[\delta^{k-l}-\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\right]. \end{align} $$
$$ \begin{align}r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r) =\delta^l\left[\delta^{k-l}-\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\right]. \end{align} $$
Since
![]() $\underline {t}_l\leq \frac {l}{n}<\frac {k}{n}\leq \overline {t}_k$
and
$\underline {t}_l\leq \frac {l}{n}<\frac {k}{n}\leq \overline {t}_k$
and
![]() $\delta ^{k-l}>\sup _{r\in [0,+\infty )}\overline {g}(r)$
, we have that
$\delta ^{k-l}>\sup _{r\in [0,+\infty )}\overline {g}(r)$
, we have that
 $$ \begin{align}\delta^{k-l}-\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)>0.\end{align} $$
$$ \begin{align}\delta^{k-l}-\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)>0.\end{align} $$
Inserting the above inequality into (3.9), we have that
 $$ \begin{align*}r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r)>0.\end{align*} $$
$$ \begin{align*}r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r)>0.\end{align*} $$
Since
 $-\dfrac {\underline {t}_l}{\overline {t}_k}>-\dfrac {k\underline {t}_l}{l\overline {t}_k}$
, we have that
$-\dfrac {\underline {t}_l}{\overline {t}_k}>-\dfrac {k\underline {t}_l}{l\overline {t}_k}$
, we have that
 $$ \begin{align*} 0<r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r)<r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r),\end{align*} $$
$$ \begin{align*} 0<r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r)<r^{\frac{k}{\overline{t}_k}}h^{k}(r) -\dfrac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}h^{l}(r),\end{align*} $$
that is, (3.8).
By the implicit function theorem and the existence and uniqueness of solutions of (3.4), (3.7) admits a unique function
![]() $h(r):=h(r,\delta ):=h(r,\delta ,\theta _1)$
. Moreover,
$h(r):=h(r,\delta ):=h(r,\delta ,\theta _1)$
. Moreover,
 $$ \begin{align} \frac{\partial h}{\partial \delta}=&\frac{k\delta^{l-1}\left[\delta^{k-l}-\frac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\right]} {kr^{\frac{l}{\underline{t}_l}}h^{l-1}[r^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}h^{k-l}-\frac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)]}>0. \end{align} $$
$$ \begin{align} \frac{\partial h}{\partial \delta}=&\frac{k\delta^{l-1}\left[\delta^{k-l}-\frac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\right]} {kr^{\frac{l}{\underline{t}_l}}h^{l-1}[r^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}h^{k-l}-\frac{\underline{t}_l}{\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)]}>0. \end{align} $$
By (3.9), we have that
 $$ \begin{align*}h^{l}(r)\left[r^{\frac{k}{\overline{t}_k}}h^{k-l}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}\right] =\delta^l\left[\delta^{k-l}-\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\right]. \end{align*} $$
$$ \begin{align*}h^{l}(r)\left[r^{\frac{k}{\overline{t}_k}}h^{k-l}(r) -\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)r^{\frac{l}{\underline{t}_l}}\right] =\delta^l\left[\delta^{k-l}-\dfrac{k\underline{t}_l}{l\overline{t}_k}\theta_1^{\frac{k}{\overline{t}_k}-\frac{l}{\underline{t}_l}}\overline{g}(\theta_1)\right]. \end{align*} $$
As
![]() $\delta \to +\infty ,$
the right side of the above equality tends to
$\delta \to +\infty ,$
the right side of the above equality tends to
![]() $+\infty $
. Since h is increasing in
$+\infty $
. Since h is increasing in
![]() $\delta $
by (3.11), we can conclude that
$\delta $
by (3.11), we can conclude that
![]() $h(r,\delta ,\theta _1)\to +\infty $
, as
$h(r,\delta ,\theta _1)\to +\infty $
, as
![]() $\delta \to +\infty $
. This lemma is proved.
$\delta \to +\infty $
. This lemma is proved.
The asymptotic behavior of w can be given as follows.
Lemma 3.3 As
![]() $r\to \infty ,$
$r\to \infty ,$
 $$ \begin{align} w(r)=\displaystyle\int_{0}^r\theta h_0(\theta)d \theta+\mu_{\beta_1,\eta}(\delta)+ \begin{cases} O(r^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(r^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln r),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align} $$
$$ \begin{align} w(r)=\displaystyle\int_{0}^r\theta h_0(\theta)d \theta+\mu_{\beta_1,\eta}(\delta)+ \begin{cases} O(r^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(r^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln r),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align} $$
where
Proof Let
![]() $h_0$
satisfy (1.15). From the equation in (1.15), we have that
$h_0$
satisfy (1.15). From the equation in (1.15), we have that
 $$ \begin{align*}\dfrac{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h_0(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h_0(r)^k+\overline{t}_k r h_0(r)^{k-1}h_0^{\prime}(r)]}{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h_0(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h_0(r)^l+\underline{t}_l r h_0(r)^{l-1}h_0^{\prime}(r)]}=g_0(r),\ r>0.\end{align*} $$
$$ \begin{align*}\dfrac{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h_0(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h_0(r)^k+\overline{t}_k r h_0(r)^{k-1}h_0^{\prime}(r)]}{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h_0(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h_0(r)^l+\underline{t}_l r h_0(r)^{l-1}h_0^{\prime}(r)]}=g_0(r),\ r>0.\end{align*} $$
It follows that
 $$ \begin{align} \dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=g_0(r),r>0. \end{align} $$
$$ \begin{align} \dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=g_0(r),r>0. \end{align} $$
Integrating the above equality on both sides, we have that
 $$ \begin{align} h_0(r)=\left(r^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \displaystyle\int_0^r g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0 (s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime} ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}}. \end{align} $$
$$ \begin{align} h_0(r)=\left(r^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \displaystyle\int_0^r g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0 (s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime} ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}}. \end{align} $$
Rewrite
![]() $w(r)$
as
$w(r)$
as
 $$ \begin{align} w(r) &=\beta_1+\int_{\eta}^{+\infty}\theta h(\theta)d\theta-\int_{r}^{+\infty}\theta h(\theta)d\theta\nonumber\\&=\beta_1+\int_{\eta}^{+\infty}\theta h(\theta)d\theta+\int_{0}^r\theta h_0(\theta)d\theta-\int_{0}^r\theta h_0(\theta)d\theta -\int_{r}^{+\infty}\theta h(\theta)d\theta\nonumber\\&=\beta_1+\int_{\eta}^{+\infty}\theta h(\theta)d\theta+\int_{0}^r\theta h_0(\theta)d\theta-\int_{0}^\eta\theta h_0(\theta)d\theta-\int_\eta^{+\infty}\theta h_0(\theta)d\theta\nonumber\\&\quad +\int_{r}^{+\infty}\theta h_0(\theta)d\theta-\int_{r}^{+\infty}\theta h(\theta)d\theta\nonumber\\&=\int_{0}^r\theta h_0(\theta)d\theta+\beta_1-\int_{0}^\eta \theta h_0(\theta)d\theta+\int_{\eta}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\&\quad -\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\&=\int_{0}^r\theta h_0(\theta)d\theta+\mu_{\beta_1,\eta}(\delta)-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta, \end{align} $$
$$ \begin{align} w(r) &=\beta_1+\int_{\eta}^{+\infty}\theta h(\theta)d\theta-\int_{r}^{+\infty}\theta h(\theta)d\theta\nonumber\\&=\beta_1+\int_{\eta}^{+\infty}\theta h(\theta)d\theta+\int_{0}^r\theta h_0(\theta)d\theta-\int_{0}^r\theta h_0(\theta)d\theta -\int_{r}^{+\infty}\theta h(\theta)d\theta\nonumber\\&=\beta_1+\int_{\eta}^{+\infty}\theta h(\theta)d\theta+\int_{0}^r\theta h_0(\theta)d\theta-\int_{0}^\eta\theta h_0(\theta)d\theta-\int_\eta^{+\infty}\theta h_0(\theta)d\theta\nonumber\\&\quad +\int_{r}^{+\infty}\theta h_0(\theta)d\theta-\int_{r}^{+\infty}\theta h(\theta)d\theta\nonumber\\&=\int_{0}^r\theta h_0(\theta)d\theta+\beta_1-\int_{0}^\eta \theta h_0(\theta)d\theta+\int_{\eta}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\&\quad -\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\&=\int_{0}^r\theta h_0(\theta)d\theta+\mu_{\beta_1,\eta}(\delta)-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta, \end{align} $$
where
By (3.4),
 $$ \begin{align*}\dfrac{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r)]}{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h(r)^l+\underline{t}_l r h(r)^{l-1}h'(r)]}=\overline{g}(r),\ r>1.\end{align*} $$
$$ \begin{align*}\dfrac{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h(r)^k+\overline{t}_k r h(r)^{k-1}h'(r)]}{\frac{k-l}{\overline{t}_k-\underline{t}_l}r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-1}h(r)^{\frac{k\underline{t}_l-l\overline{t}_k}{\overline{t}_k-\underline{t}_l}}[h(r)^l+\underline{t}_l r h(r)^{l-1}h'(r)]}=\overline{g}(r),\ r>1.\end{align*} $$
It follows that
 $$ \begin{align} \dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=\overline{g}(r),r>1,\end{align} $$
$$ \begin{align} \dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=\overline{g}(r),r>1,\end{align} $$
that is,
Integrating the above equality from
![]() $1$
to r, we obtain that
$1$
to r, we obtain that
It follows that
 $$ \begin{align}h(r)=\left(\delta^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}r^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +r^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \displaystyle\int_1^r\overline{g}(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} \end{align} $$
$$ \begin{align}h(r)=\left(\delta^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}r^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +r^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \displaystyle\int_1^r\overline{g}(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} \end{align} $$
and
 $$ \begin{align*}w(r)&=\beta_1+\int_{\eta}^{r}\theta \left(\delta^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\right. \\& \qquad\qquad\ \qquad \times \left.\displaystyle\int_1^\theta\overline{g}(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} d\theta,\ \forall \ r\geq \eta>1. \end{align*} $$
$$ \begin{align*}w(r)&=\beta_1+\int_{\eta}^{r}\theta \left(\delta^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\right. \\& \qquad\qquad\ \qquad \times \left.\displaystyle\int_1^\theta\overline{g}(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} d\theta,\ \forall \ r\geq \eta>1. \end{align*} $$
Since by (3.2),
![]() $\overline {g}(r)=g_0(r)+C_1r^{-\beta }, r>\theta _{0}$
, then the last term in (3.16) is
$\overline {g}(r)=g_0(r)+C_1r^{-\beta }, r>\theta _{0}$
, then the last term in (3.16) is
 $$ \begin{align} &-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left(\delta^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \displaystyle\int_1^\theta\overline{g}(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left[\delta_0 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta \left(g_0(s)+C_1s^{-\beta}\right)\left(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\right)^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left[\delta_0 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\left(\int_{0}^\theta g_0(s)\left(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\right)^{\prime}ds \right. \right.\right. \nonumber\\& \qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad \left.-\int_{0}^{\theta_{0}}g_0(s)\left(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\right)^{\prime}ds\right)\nonumber\\& \qquad\quad\qquad\qquad \left.\left.+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta,\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left[\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds \right. \right.\nonumber\\& \qquad\quad\qquad \left.\left. +\ \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta \nonumber\\=&-\int_{r}^{+\infty}\theta h_0(\theta)\left\{\left[\frac{\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+\frac{\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+1 \right. \right.\nonumber\\& \qquad\qquad\qquad\qquad\left.\left. +\ \frac{\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} \right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -1\right\}d\theta,\nonumber\\ \end{align} $$
$$ \begin{align} &-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left(\delta^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \displaystyle\int_1^\theta\overline{g}(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left[\delta_0 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta \left(g_0(s)+C_1s^{-\beta}\right)\left(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\right)^{\prime}ds\right)^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left[\delta_0 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\left(\int_{0}^\theta g_0(s)\left(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\right)^{\prime}ds \right. \right.\right. \nonumber\\& \qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad \left.-\int_{0}^{\theta_{0}}g_0(s)\left(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\right)^{\prime}ds\right)\nonumber\\& \qquad\quad\qquad\qquad \left.\left.+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta,\nonumber\\=&-\int_{r}^{+\infty}\theta\left\{\left[\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds \right. \right.\nonumber\\& \qquad\quad\qquad \left.\left. +\ \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -h_0(\theta)\right\}d\theta \nonumber\\=&-\int_{r}^{+\infty}\theta h_0(\theta)\left\{\left[\frac{\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+\frac{\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+1 \right. \right.\nonumber\\& \qquad\qquad\qquad\qquad\left.\left. +\ \frac{\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} \right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -1\right\}d\theta,\nonumber\\ \end{align} $$
where
![]() $\delta _0=\delta ^{\frac {(k-l)\overline {t}_k}{\overline {t}_k-\underline {t}_l}}+\int _1^{\theta _{0}} \overline {g}(s)(s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }ds$
and
$\delta _0=\delta ^{\frac {(k-l)\overline {t}_k}{\overline {t}_k-\underline {t}_l}}+\int _1^{\theta _{0}} \overline {g}(s)(s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }ds$
and
 $\delta _1=\delta _0-\int _{0}^{\theta _{0}}g_0(s) (s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }ds$
. In (3.19), we let
$\delta _1=\delta _0-\int _{0}^{\theta _{0}}g_0(s) (s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }ds$
. In (3.19), we let
Then, if
![]() $\beta \not =\frac {k-l}{\overline {t}_k-\underline {t}_l}$
,
$\beta \not =\frac {k-l}{\overline {t}_k-\underline {t}_l}$
,
 $$ \begin{align} Q(\theta) &=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\nonumber\\&=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\left(C_1\theta^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}(\theta) -C_1\theta_0^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}(\theta_0)\right. \nonumber\\& \quad\qquad\qquad \left.+C_1\beta \int_{\theta_{0}}^\theta s^{-\beta-1}s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}ds\right)\nonumber\\&=C_2\theta^{-\beta}+C_3\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+C_1\beta h(\kappa_0)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \int_{\theta_{0}}^\theta s^{-\beta-1}s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}ds\end{align} $$
$$ \begin{align} Q(\theta) &=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{\theta_{0}}^\theta C_1s^{-\beta}(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\nonumber\\&=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\left(C_1\theta^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}(\theta) -C_1\theta_0^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}(\theta_0)\right. \nonumber\\& \quad\qquad\qquad \left.+C_1\beta \int_{\theta_{0}}^\theta s^{-\beta-1}s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}ds\right)\nonumber\\&=C_2\theta^{-\beta}+C_3\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+C_1\beta h(\kappa_0)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \int_{\theta_{0}}^\theta s^{-\beta-1}s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}ds\end{align} $$
 $$ \begin{align} &=C_2\theta^{-\beta}+C_3\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +\frac{C_1\beta h(\kappa_0)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k- \underline{t}_l}}}{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}\theta^{-\beta} -\frac{C_1\beta h(\kappa_0)^{\frac{(k-l) \underline{t}_l}{\overline{t}_k-\underline{t}_l}}}{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}\theta_0^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta} \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \nonumber\\&=C_4\theta^{-\beta}+C_5\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}, \end{align} $$
$$ \begin{align} &=C_2\theta^{-\beta}+C_3\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +\frac{C_1\beta h(\kappa_0)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k- \underline{t}_l}}}{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}\theta^{-\beta} -\frac{C_1\beta h(\kappa_0)^{\frac{(k-l) \underline{t}_l}{\overline{t}_k-\underline{t}_l}}}{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta}\theta_0^{\frac{k-l}{\overline{t}_k-\underline{t}_l}-\beta} \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} \nonumber\\&=C_4\theta^{-\beta}+C_5\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}, \end{align} $$
where
![]() $C_2:=C_2(\theta )=C_1h^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}(\theta )$
and
$C_2:=C_2(\theta )=C_1h^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}(\theta )$
and
![]() $C_3=-C_1\theta _0^{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }h^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}(\theta _0)$
. In (3.20), we employ the integration by parts and the mean value theorem of integrals and
$C_3=-C_1\theta _0^{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }h^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}(\theta _0)$
. In (3.20), we employ the integration by parts and the mean value theorem of integrals and
![]() $\kappa _0\in [\theta _0,\theta ]$
,
$\kappa _0\in [\theta _0,\theta ]$
,
 $C_4=C_2+\frac {C_1\beta h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}}{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }$
,
$C_4=C_2+\frac {C_1\beta h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}}{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }$
,
 $C_5=C_3-\frac {C_1\beta h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k- \underline {t}_l}}}{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }\theta _0^{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }.$
$C_5=C_3-\frac {C_1\beta h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k- \underline {t}_l}}}{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }\theta _0^{\frac {k-l}{\overline {t}_k-\underline {t}_l}-\beta }.$
In (3.19), we set
 $$ \begin{align}R(\theta)&:=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)\nonumber\\&=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\nonumber\\&=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)\left((s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime} -(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}\right)ds.\nonumber\\ \end{align} $$
$$ \begin{align}R(\theta)&:=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)\nonumber\\&=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds\nonumber\\&=\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)\left((s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime} -(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}\right)ds.\nonumber\\ \end{align} $$
According to (3.14) and (3.17), we can have that
 $$ \begin{align*}\lim_{r\to +\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} \dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=\lim_{r\to+\infty}\dfrac{\overline{g}(r)}{g_0(r)}=1.\end{align*} $$
$$ \begin{align*}\lim_{r\to +\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} \dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=\lim_{r\to+\infty}\dfrac{\overline{g}(r)}{g_0(r)}=1.\end{align*} $$
Consequently,
 $$ \begin{align}\lim_{r\to +\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} =\lim_{r\to +\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}.\end{align} $$
$$ \begin{align}\lim_{r\to +\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} =\lim_{r\to +\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}.\end{align} $$
On the other hand, in light of (3.14) and (3.17), we know that
and
As a result,
 $$ \begin{align}\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}}=& \lim_{r\to+\infty}\dfrac{\overline{g}(r)(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {g_0(r)(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=\lim_{r\to+\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}. \end{align} $$
$$ \begin{align}\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}}=& \lim_{r\to+\infty}\dfrac{\overline{g}(r)(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {g_0(r)(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}=\lim_{r\to+\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}}. \end{align} $$
Likewise, we also have that
 $$ \begin{align}\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}= \lim_{r\to+\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}}. \end{align} $$
$$ \begin{align}\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}= \lim_{r\to+\infty}\dfrac{(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}} {(r^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}})^{\prime}}. \end{align} $$
From (3.23)–(3.25), we get that
 $$ \begin{align*}\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}} =\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}.\end{align*} $$
$$ \begin{align*}\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}} =\lim_{r\to+\infty}\dfrac{(h(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}{(h_0(r))^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}}.\end{align*} $$
So
 $$ \begin{align*}\lim_{r\to+\infty}\dfrac{h(r)}{h_0(r)}=1.\end{align*} $$
$$ \begin{align*}\lim_{r\to+\infty}\dfrac{h(r)}{h_0(r)}=1.\end{align*} $$
And, therefore, the term
 $\int _{0}^\theta g_0(s)\left ((s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime } -(s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h_0(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }\right )ds$
in (3.22) is bounded and thus
$\int _{0}^\theta g_0(s)\left ((s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime } -(s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h_0(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }\right )ds$
in (3.22) is bounded and thus
 $$ \begin{align}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)=C_{10}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}},\end{align} $$
$$ \begin{align}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\int_{0}^\theta g_0(s)(s^{\frac{k-l}{\overline{t}_k-\underline{t}_l}}h(s)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}})^{\prime}ds -h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)=C_{10}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}},\end{align} $$
where
 $c_{10}=c_{10}(\theta )=\int _{0}^\theta g_0(s)\left ((s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime } -(s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h_0(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }\right )ds$
. Hence, by (3.21) and (3.26), we know that
$c_{10}=c_{10}(\theta )=\int _{0}^\theta g_0(s)\left ((s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime } -(s^{\frac {k-l}{\overline {t}_k-\underline {t}_l}}h_0(s)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}})^{\prime }\right )ds$
. Hence, by (3.21) and (3.26), we know that
 $$ \begin{align} &-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta h_0(\theta)\left\{\left[\frac{\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+\frac{C_{10}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+1 +\frac{C_4\theta^{-\beta}+C_5\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} \right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -1\right\}d\theta. \nonumber\\ \end{align} $$
$$ \begin{align} &-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta h_0(\theta)\left\{\left[\frac{\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+\frac{C_{10}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+1 +\frac{C_4\theta^{-\beta}+C_5\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} \right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -1\right\}d\theta. \nonumber\\ \end{align} $$
Thus, due to the fact that
![]() $h_0$
is bounded, then (3.27) becomes
$h_0$
is bounded, then (3.27) becomes
 $$ \begin{align*} -\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta=&-\int_{r}^{+\infty}O(\theta^{1-\frac{k-l}{\overline{t}_k-\underline{t}_l}})+O(\theta^{1-\beta})d\theta\nonumber\\ =&O(r^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \ \mbox{as}\ \ r\to+\infty. \end{align*} $$
$$ \begin{align*} -\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta=&-\int_{r}^{+\infty}O(\theta^{1-\frac{k-l}{\overline{t}_k-\underline{t}_l}})+O(\theta^{1-\beta})d\theta\nonumber\\ =&O(r^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \ \mbox{as}\ \ r\to+\infty. \end{align*} $$
If
![]() $\beta =\frac {k-l}{\overline {t}_k-\underline {t}_l}$
, then by (3.20),
$\beta =\frac {k-l}{\overline {t}_k-\underline {t}_l}$
, then by (3.20),
 $$ \begin{align} Q(\theta) &=C_2\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+C_3\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +C_1\frac{k-l}{\overline{t}_k-\underline{t}_l} h(\kappa_0)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}(\ln \theta-\ln \theta_0)\nonumber\\&=C_6\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln \theta+C_7\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}, \end{align} $$
$$ \begin{align} Q(\theta) &=C_2\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}+C_3\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}} +C_1\frac{k-l}{\overline{t}_k-\underline{t}_l} h(\kappa_0)^{\frac{(k-l)\underline{t}_l}{\overline{t}_k-\underline{t}_l}}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}(\ln \theta-\ln \theta_0)\nonumber\\&=C_6\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln \theta+C_7\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}, \end{align} $$
where
![]() $C_6=C_1\frac {k-l}{\overline {t}_k-\underline {t}_l} h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}},$
$C_6=C_1\frac {k-l}{\overline {t}_k-\underline {t}_l} h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}},$
![]() $C_7:=C_2+C_3-C_1\frac {k-l}{\overline {t}_k-\underline {t}_l} h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}\ln \theta _0.$
Therefore, by (3.19), (3.22), and (3.28), we know that
$C_7:=C_2+C_3-C_1\frac {k-l}{\overline {t}_k-\underline {t}_l} h(\kappa _0)^{\frac {(k-l)\underline {t}_l}{\overline {t}_k-\underline {t}_l}}\ln \theta _0.$
Therefore, by (3.19), (3.22), and (3.28), we know that
 $$ \begin{align} &-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta h_0(\theta)\left\{\left[\frac{\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} +\frac{C_{10}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+1 +\frac{C_6\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln \theta+C_7\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} \right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -1\right\}d\theta.\nonumber\\ \end{align} $$
$$ \begin{align} &-\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta\nonumber\\=&-\int_{r}^{+\infty}\theta h_0(\theta)\left\{\left[\frac{\delta_1 \theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} +\frac{C_{10}\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)}+1 +\frac{C_6\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln \theta+C_7\theta^{-\frac{k-l}{\overline{t}_k-\underline{t}_l}}}{h_0^{\frac{(k-l)\overline{t}_k}{\overline{t}_k-\underline{t}_l}}(\theta)} \right]^{\frac{\overline{t}_k-\underline{t}_l}{(k-l)\overline{t}_k}} -1\right\}d\theta.\nonumber\\ \end{align} $$
Hence, by the fact that
![]() $h_0$
is bounded, then (3.29) turns into
$h_0$
is bounded, then (3.29) turns into
 $$ \begin{align*} -\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta=&-\int_{r}^{+\infty}O(\theta^{1-\frac{k-l}{\overline{t}_k-\underline{t}_l}})+O(\theta^{1-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln \theta)d\theta\nonumber\\ =&O(r^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln r),\ \ \mbox{as}\ \ r\to+\infty. \end{align*} $$
$$ \begin{align*} -\int_{r}^{+\infty}\theta[h(\theta)-h_0(\theta)]d\theta=&-\int_{r}^{+\infty}O(\theta^{1-\frac{k-l}{\overline{t}_k-\underline{t}_l}})+O(\theta^{1-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln \theta)d\theta\nonumber\\ =&O(r^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln r),\ \ \mbox{as}\ \ r\to+\infty. \end{align*} $$
To sum up, we can get (3.12). By Lemma 3.2(ii), we know that (3.13) holds.
Let
where
![]() $E_{\eta }:=\{x\in \mathbb {R}^n:r<\eta \}$
. Then we can conclude that such W is a generalized symmetric smooth subsolution of (1.1) as follows.
$E_{\eta }:=\{x\in \mathbb {R}^n:r<\eta \}$
. Then we can conclude that such W is a generalized symmetric smooth subsolution of (1.1) as follows.
Theorem 3.4
W is a smooth k-convex subsolution of (1.1) in
![]() $\mathbb {R}^n\setminus \bar {E}_{\eta }$
.
$\mathbb {R}^n\setminus \bar {E}_{\eta }$
.
Proof By the definition of w, we have that
![]() $w'=rh$
and
$w'=rh$
and
![]() $w"=h+rh'$
. It follows that for i,
$w"=h+rh'$
. It follows that for i,
![]() $j=1$
,
$j=1$
,
![]() $\ldots $
, n,
$\ldots $
, n,
By Lemma A.2, we have that for
![]() $j=1$
,
$j=1$
,
![]() $\ldots $
, k,
$\ldots $
, k,
 $$ \begin{align} &S_j(D^2W)=\sigma_j(\lambda(D^2W))\nonumber\\ & \quad=\sigma_j(a)h^j+\frac{h'}{r}h^{j-1}\sum_{i=1}^{n}\sigma_{j-1;i}(a)a_i^2x_i^2\nonumber\\ & \quad \geq \sigma_j(a)h^j+\overline{t}_j(a)\sigma_j(a)rh^{j-1}h'\nonumber\\ & \quad =\sigma_j(a)h^{j-1}(h+\overline{t}_j(a)rh'), \end{align} $$
$$ \begin{align} &S_j(D^2W)=\sigma_j(\lambda(D^2W))\nonumber\\ & \quad=\sigma_j(a)h^j+\frac{h'}{r}h^{j-1}\sum_{i=1}^{n}\sigma_{j-1;i}(a)a_i^2x_i^2\nonumber\\ & \quad \geq \sigma_j(a)h^j+\overline{t}_j(a)\sigma_j(a)rh^{j-1}h'\nonumber\\ & \quad =\sigma_j(a)h^{j-1}(h+\overline{t}_j(a)rh'), \end{align} $$
where we have used the facts that
![]() $h\geq \overline {g}^{\frac {1}{k-l}}>0$
and
$h\geq \overline {g}^{\frac {1}{k-l}}>0$
and
![]() $h'\leq 0$
for any
$h'\leq 0$
for any
![]() $r\geq 1$
by Lemma 3.2(i).
$r\geq 1$
by Lemma 3.2(i).
Since
![]() $l<k$
,
$l<k$
,
![]() $\underline {t}_l\leq \underline {t}_k\leq \frac {k}{n}\leq \overline {t}_k$
, then
$\underline {t}_l\leq \underline {t}_k\leq \frac {k}{n}\leq \overline {t}_k$
, then
![]() $-\frac {\underline {t}_l}{\overline {t}_k}\geq -1.$
It follows that
$-\frac {\underline {t}_l}{\overline {t}_k}\geq -1.$
It follows that
 $$ \begin{align*}0\leq \frac{h^{k-l}-\overline{g}(r)}{h^{k-l}-\overline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}\leq 1\leq \frac{\overline{t}_k}{\overline{t}_j}, j\leq k,\end{align*} $$
$$ \begin{align*}0\leq \frac{h^{k-l}-\overline{g}(r)}{h^{k-l}-\overline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}\leq 1\leq \frac{\overline{t}_k}{\overline{t}_j}, j\leq k,\end{align*} $$
and
 $$ \begin{align*}h^{\prime}=&-\frac{1}{r}\dfrac{h}{\overline{t}_k}\dfrac{h(r)^{k-l}-\overline{g}(r)}{h(r)^{k-l}-\overline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}\geq-\frac{1}{r}\dfrac{h}{\overline{t}_k}\frac{\overline{t}_k}{\overline{t}_j}=-\frac{1}{r}\dfrac{h}{\overline{t}_j}. \end{align*} $$
$$ \begin{align*}h^{\prime}=&-\frac{1}{r}\dfrac{h}{\overline{t}_k}\dfrac{h(r)^{k-l}-\overline{g}(r)}{h(r)^{k-l}-\overline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}\geq-\frac{1}{r}\dfrac{h}{\overline{t}_k}\frac{\overline{t}_k}{\overline{t}_j}=-\frac{1}{r}\dfrac{h}{\overline{t}_j}. \end{align*} $$
Thus,
![]() $h+\overline {t}_jrh^{\prime }\geq 0.$
Hence, by (3.30),
$h+\overline {t}_jrh^{\prime }\geq 0.$
Hence, by (3.30),
![]() $S_j(D^2w)\geq 0$
for
$S_j(D^2w)\geq 0$
for
![]() $j=1,\dots ,k.$
Moreover, by (3.5) and the fact that
$j=1,\dots ,k.$
Moreover, by (3.5) and the fact that
![]() $\sigma _{k}(a)=\sigma _{l}(a)$
, we have that for any
$\sigma _{k}(a)=\sigma _{l}(a)$
, we have that for any
![]() $x\in \mathbb {R}^n\setminus \bar {E}_{\eta }$
,
$x\in \mathbb {R}^n\setminus \bar {E}_{\eta }$
,
 $$ \begin{align*} &\frac{S_k(D^2W)}{S_l(D^2W)}=\frac{\sigma_k(\lambda(D^2W))}{\sigma_l(\lambda(D^2W))}\\ & \quad =\frac{\sigma_k(a)h^k+\frac{h'}{r}h^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2}{\sigma_l(a)h^l+\frac{h'}{r}h^{l-1}\sum_{i=1}^{n}\sigma_{l-1;i}(a)a_i^2x_i^2}\\ & \quad \geq \frac{\sigma_k(a)h^k+\overline{t}_k(a)\sigma_k(a)rh^{k-1}h'}{\sigma_l(a)h^l+\underline{t}_l(a) \sigma_l(a)rh^{l-1}h'}\\ & \quad =\frac{h^k+\overline{t}_k(a)rh^{k-1}h'}{h^l+\underline{t}_l(a)rh^{l-1}h'}\\ & \quad =\overline{g}(r)\geq g(x). \end{align*} $$
$$ \begin{align*} &\frac{S_k(D^2W)}{S_l(D^2W)}=\frac{\sigma_k(\lambda(D^2W))}{\sigma_l(\lambda(D^2W))}\\ & \quad =\frac{\sigma_k(a)h^k+\frac{h'}{r}h^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2}{\sigma_l(a)h^l+\frac{h'}{r}h^{l-1}\sum_{i=1}^{n}\sigma_{l-1;i}(a)a_i^2x_i^2}\\ & \quad \geq \frac{\sigma_k(a)h^k+\overline{t}_k(a)\sigma_k(a)rh^{k-1}h'}{\sigma_l(a)h^l+\underline{t}_l(a) \sigma_l(a)rh^{l-1}h'}\\ & \quad =\frac{h^k+\overline{t}_k(a)rh^{k-1}h'}{h^l+\underline{t}_l(a)rh^{l-1}h'}\\ & \quad =\overline{g}(r)\geq g(x). \end{align*} $$
Then we complete the proof.
Next we shall construct the generalized symmetric supersolution of (1.1) of the form
where
![]() $\beta _{2}\in {\mathbb R}$
and H is obtained from the following lemma.
$\beta _{2}\in {\mathbb R}$
and H is obtained from the following lemma.
Lemma 3.5 For
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $0\leq l<k\leq n$
. Let
$0\leq l<k\leq n$
. Let
![]() $\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(1)<\tau ^{k-l}<\underline {g}(1)$
. Then the problem
$\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(1)<\tau ^{k-l}<\underline {g}(1)$
. Then the problem
 $$ \begin{align} \begin{cases} \dfrac{H(r)^k+\overline{t}_k r H(r)^{k-1}H'(r)}{H(r)^l+\underline{t}_l r H(r)^{l-1}H'(r)}=\underline{g}(r),\ r>1,\\ H(1)=\tau \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \dfrac{H(r)^k+\overline{t}_k r H(r)^{k-1}H'(r)}{H(r)^l+\underline{t}_l r H(r)^{l-1}H'(r)}=\underline{g}(r),\ r>1,\\ H(1)=\tau \end{cases} \end{align} $$
admits a smooth solution
![]() $H(r)=H(r,\tau )$
on
$H(r)=H(r,\tau )$
on
![]() $[1,+\infty )$
satisfying:
$[1,+\infty )$
satisfying:
-
(i)
 $\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(r) <H^{k-l}(r,\tau )<\underline {g}(r),\partial _{r}H(r,\tau )\geq 0$
for
$\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(r) <H^{k-l}(r,\tau )<\underline {g}(r),\partial _{r}H(r,\tau )\geq 0$
for
 $r\geq 1$
.
$r\geq 1$
. -
(ii)
 $H(r,\tau )$
is continuous and strictly increasing with respect to
$H(r,\tau )$
is continuous and strictly increasing with respect to
 $\tau $
.
$\tau $
.
Proof For brevity, we sometimes write
![]() $H(r)$
or
$H(r)$
or
![]() $H(r,\tau )$
when there is no confusion. From (3.31), we have
$H(r,\tau )$
when there is no confusion. From (3.31), we have
 $$ \begin{align} \begin{cases}\displaystyle\frac{\mbox{d} H}{\mbox{d}r}=-\frac{1}{r}\dfrac{H}{\overline{t}_k}\dfrac{H(r)^{k-l}- \underline{g}(r)}{H(r)^{k-l}-\underline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}},\ r>1,\\ H(1)=\tau. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases}\displaystyle\frac{\mbox{d} H}{\mbox{d}r}=-\frac{1}{r}\dfrac{H}{\overline{t}_k}\dfrac{H(r)^{k-l}- \underline{g}(r)}{H(r)^{k-l}-\underline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}},\ r>1,\\ H(1)=\tau. \end{cases} \end{align} $$
Since
![]() $\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(1)<\tau ^{k-l}<\underline {g}(1)$
and
$\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(1)<\tau ^{k-l}<\underline {g}(1)$
and
![]() $\underline {g}(r)$
is strictly increasing, by the existence, uniqueness, and extension theorem for the solution of the initial value problem of the ODE, we can get that the problem has a smooth solution
$\underline {g}(r)$
is strictly increasing, by the existence, uniqueness, and extension theorem for the solution of the initial value problem of the ODE, we can get that the problem has a smooth solution
![]() $H(r,\delta )$
satisfying
$H(r,\delta )$
satisfying
![]() $\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(r)<H^{k-l}(r,\tau )<\underline {g}(r),$
and
$\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(r)<H^{k-l}(r,\tau )<\underline {g}(r),$
and
![]() $\partial _{r}H(r,\tau )\geq 0$
, that is, (i) of this lemma.
$\partial _{r}H(r,\tau )\geq 0$
, that is, (i) of this lemma.
Let
 $$ \begin{align*}p(H):=p(H(r,\tau)):=\dfrac{H(r,\tau)}{\overline{t}_k}\dfrac{H(r,\tau)^{k-l} -\underline{g}(r)}{H(r,\tau)^{k-l}-\underline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}.\end{align*} $$
$$ \begin{align*}p(H):=p(H(r,\tau)):=\dfrac{H(r,\tau)}{\overline{t}_k}\dfrac{H(r,\tau)^{k-l} -\underline{g}(r)}{H(r,\tau)^{k-l}-\underline{g}(r)\frac{\underline{t}_l}{\overline{t}_k}}.\end{align*} $$
Then (3.32) becomes
 $$ \begin{align} \begin{cases}\displaystyle\frac{\partial H}{\partial r}=-\frac{1}{r}p(H(r,\tau)),\ r>1,\\ H(1,\tau)=\tau. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases}\displaystyle\frac{\partial H}{\partial r}=-\frac{1}{r}p(H(r,\tau)),\ r>1,\\ H(1,\tau)=\tau. \end{cases} \end{align} $$
Differentiating (3.33) with
![]() $\tau $
, we have that
$\tau $
, we have that
 $$ \begin{align*}\begin{cases}\displaystyle\frac{\partial^2 H}{\partial r\partial \tau}=-\frac{1}{r}p^{\prime}(H)\dfrac{\partial H}{\partial \tau},\\ \dfrac{\partial H(1,\tau)}{\partial \tau}=1. \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases}\displaystyle\frac{\partial^2 H}{\partial r\partial \tau}=-\frac{1}{r}p^{\prime}(H)\dfrac{\partial H}{\partial \tau},\\ \dfrac{\partial H(1,\tau)}{\partial \tau}=1. \end{cases} \end{align*} $$
It follows that
that is, (ii) of this lemma.
Remark 3.6 If
![]() $g\equiv 1$
, then we choose
$g\equiv 1$
, then we choose
![]() $\overline {g}\equiv \underline {g}\equiv 1,\delta =\tau =1$
. Then
$\overline {g}\equiv \underline {g}\equiv 1,\delta =\tau =1$
. Then
![]() $h\equiv 1$
and
$h\equiv 1$
and
![]() $H\equiv 1$
satisfy (3.4) and (3.32), respectively.
$H\equiv 1$
satisfy (3.4) and (3.32), respectively.
Analogous to (3.12),
 $$ \begin{align} \psi(r)=\displaystyle\int_{0}^r\theta h_0(\theta)d\theta+\nu_{\beta_2,\eta}(\tau)+ \begin{cases} O(r^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(r^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln r),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align} $$
$$ \begin{align} \psi(r)=\displaystyle\int_{0}^r\theta h_0(\theta)d\theta+\nu_{\beta_2,\eta}(\tau)+ \begin{cases} O(r^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(r^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln r),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align} $$
as
![]() $r\to +\infty $
, where
$r\to +\infty $
, where
Theorem 3.7
![]() $\Psi $
is a k-convex supersolution of (1.1) in
$\Psi $
is a k-convex supersolution of (1.1) in
![]() $\mathbb {R}^n\backslash E_{\eta }$
.
$\mathbb {R}^n\backslash E_{\eta }$
.
Proof By Lemma A.2, we have that for
![]() $j=1$
,
$j=1$
,
![]() $\ldots $
, k,
$\ldots $
, k,
 $$ \begin{align*} S_j(D^2\Psi)&=\sigma_j(\lambda(D^2\Psi))\\ &=\sigma_j(a)H(r)^j+\frac{H'(r)}{r}H(r)^{j-1}\sum_{i=1}^{n}\sigma_{j-1;i}(a)a_i^2x_i^2\geq0, \end{align*} $$
$$ \begin{align*} S_j(D^2\Psi)&=\sigma_j(\lambda(D^2\Psi))\\ &=\sigma_j(a)H(r)^j+\frac{H'(r)}{r}H(r)^{j-1}\sum_{i=1}^{n}\sigma_{j-1;i}(a)a_i^2x_i^2\geq0, \end{align*} $$
where we have used the fact that
![]() $H'\geq 0$
by Lemma 3.5(i). Moreover, by (3.31), we have that for any
$H'\geq 0$
by Lemma 3.5(i). Moreover, by (3.31), we have that for any
![]() $x\in \mathbb {R}^n\backslash E_{\eta }$
,
$x\in \mathbb {R}^n\backslash E_{\eta }$
,
 $$ \begin{align} \frac{S_k(D^2\Psi)}{S_l(D^2\Psi)}&=\frac{\sigma_k(\lambda(D^2\Psi))}{\sigma_l(\lambda(D^2\Psi))}\nonumber\\ &=\frac{\sigma_k(a)H(r)^k+\frac{H'(r)}{r}H(r)^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2} {\sigma_l(a)H(r)^l+\frac{H'(r)}{r}H(r)^{l-1}\sum_{i=1}^{n}\sigma_{l-1;i}(a)a_i^2x_i^2}\nonumber\\ &\leq \frac{H(r)^k+\overline{t}_k rH(r)^{k-1}H'}{H(r)^l+\overline{t}_l rH(r)^{l-1}H'}\nonumber\\ &=\underline{g}(r)\leq g(x). \end{align} $$
$$ \begin{align} \frac{S_k(D^2\Psi)}{S_l(D^2\Psi)}&=\frac{\sigma_k(\lambda(D^2\Psi))}{\sigma_l(\lambda(D^2\Psi))}\nonumber\\ &=\frac{\sigma_k(a)H(r)^k+\frac{H'(r)}{r}H(r)^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2} {\sigma_l(a)H(r)^l+\frac{H'(r)}{r}H(r)^{l-1}\sum_{i=1}^{n}\sigma_{l-1;i}(a)a_i^2x_i^2}\nonumber\\ &\leq \frac{H(r)^k+\overline{t}_k rH(r)^{k-1}H'}{H(r)^l+\overline{t}_l rH(r)^{l-1}H'}\nonumber\\ &=\underline{g}(r)\leq g(x). \end{align} $$
4 Proof of Theorem 1.6
Before proving Theorem 1.6, we will first give some lemmas which will be used later.
Lemma 4.1 Suppose that
![]() $\phi \in C^{2}(\partial \Omega )$
. Then there exists some constant C, depending only on
$\phi \in C^{2}(\partial \Omega )$
. Then there exists some constant C, depending only on
![]() $g,~ n, ||\phi ||_{C^{2}(\partial \Omega )},$
the upper bound of A, the diameter and the convexity of
$g,~ n, ||\phi ||_{C^{2}(\partial \Omega )},$
the upper bound of A, the diameter and the convexity of
![]() $\Omega $
, and the
$\Omega $
, and the
![]() $C^{2}$
norm of
$C^{2}$
norm of
![]() $\partial \Omega $
, such that, for each
$\partial \Omega $
, such that, for each
![]() $\varsigma \in \partial \Omega $
, there exists
$\varsigma \in \partial \Omega $
, there exists
![]() $\overline {x}(\varsigma )\in \mathbb {R}^{n}$
such that
$\overline {x}(\varsigma )\in \mathbb {R}^{n}$
such that
![]() $|\overline {x}(\varsigma )|\leq C$
,
$|\overline {x}(\varsigma )|\leq C$
,
where
and
![]() $\frac {\binom {n}{k}\Xi ^k}{\binom {n}{l}\Xi ^l}>\sup \limits _{E_{2R}}\overline {g}$
for some
$\frac {\binom {n}{k}\Xi ^k}{\binom {n}{l}\Xi ^l}>\sup \limits _{E_{2R}}\overline {g}$
for some
![]() $R>0$
such that
$R>0$
such that
![]() $E_{1}\subset \subset \Omega \subset \subset E_{R}$
.
$E_{1}\subset \subset \Omega \subset \subset E_{R}$
.
Proof The proof of Lemma 4.1 is similar to the proof of Lemma 3.1 in [Reference Cao and Bao9]. We only substitute the constant
![]() $F^{\frac {1}{k}}$
in Lemma 3.1 in [Reference Cao and Bao9] with
$F^{\frac {1}{k}}$
in Lemma 3.1 in [Reference Cao and Bao9] with
![]() $\Xi $
. Here, we omit its proof.
$\Xi $
. Here, we omit its proof.
Lemma 4.2 [Reference Dai11, Lemma 2.2]
Let B be a ball in
![]() $\mathbb {R}^n$
, and let
$\mathbb {R}^n$
, and let
![]() $f\in C^0(\overline {B})$
be nonnegative. Suppose that
$f\in C^0(\overline {B})$
be nonnegative. Suppose that
![]() $\underline {u}\in C^0(\overline {B})$
satisfies
$\underline {u}\in C^0(\overline {B})$
satisfies
![]() $S_k(D^2\underline {u})\geq f(x)$
$S_k(D^2\underline {u})\geq f(x)$
![]() $\mbox { in } B$
in the viscosity sense. Then the Dirichlet problem
$\mbox { in } B$
in the viscosity sense. Then the Dirichlet problem
 $$ \begin{align*} \dfrac{S_{k}(D^{2}u)}{S_{l}(D^{2}u)}&=f(x),\ \ x\in B,\\ u&=\underline{u}(x),\ \ x\in \partial B \end{align*} $$
$$ \begin{align*} \dfrac{S_{k}(D^{2}u)}{S_{l}(D^{2}u)}&=f(x),\ \ x\in B,\\ u&=\underline{u}(x),\ \ x\in \partial B \end{align*} $$
admits a unique k-convex viscosity solution
![]() $u\in C^0(\overline {B})$
.
$u\in C^0(\overline {B})$
.
Lemma 4.3 [Reference Dai11, Lemma 2.3]
Let D be a domain in
![]() $\mathbb {R}^n$
, and let
$\mathbb {R}^n$
, and let
![]() $f\in C^{0}(\mathbb {R}^n)$
be nonnegative. Assume that
$f\in C^{0}(\mathbb {R}^n)$
be nonnegative. Assume that
![]() $v\in C^{0}(\overline {D})$
and
$v\in C^{0}(\overline {D})$
and
![]() $u\in C^{0}(\mathbb {R}^n)$
are two k-convex functions satisfying in the viscosity sense
$u\in C^{0}(\mathbb {R}^n)$
are two k-convex functions satisfying in the viscosity sense
 $$ \begin{align*}\dfrac{S_{k}(D^{2}v)}{S_{l}(D^{2}v)}\geq f(x),x\in D,\end{align*} $$
$$ \begin{align*}\dfrac{S_{k}(D^{2}v)}{S_{l}(D^{2}v)}\geq f(x),x\in D,\end{align*} $$
and
 $$ \begin{align*}\dfrac{S_{k}(D^{2}u)}{S_{l}(D^{2}u)}\geq f(x),x\in \mathbb{R}^n,\end{align*} $$
$$ \begin{align*}\dfrac{S_{k}(D^{2}u)}{S_{l}(D^{2}u)}\geq f(x),x\in \mathbb{R}^n,\end{align*} $$
respectively,
![]() $u\leq v$
on
$u\leq v$
on
![]() $\overline {D}$
and
$\overline {D}$
and
![]() $u=v$
on
$u=v$
on
![]() $\partial D$
.
$\partial D$
.
Let
 $$ \begin{align*}w(x):=\left\{ \begin{array}{@{}lll} v(x),&x\in D,\\ u(x),&x\in \mathbb{R}^n\backslash D. \end{array} \right. \end{align*} $$
$$ \begin{align*}w(x):=\left\{ \begin{array}{@{}lll} v(x),&x\in D,\\ u(x),&x\in \mathbb{R}^n\backslash D. \end{array} \right. \end{align*} $$
Then
![]() $w\in C^{0}(\mathbb {R}^n)$
is a k-convex function satisfying
$w\in C^{0}(\mathbb {R}^n)$
is a k-convex function satisfying
 $$ \begin{align*}\dfrac{S_{k}(D^{2}w)}{S_{l}(D^{2}w)}\geq f(x)~~\mbox{in}~\mathbb{R}^n~~~~\mbox{in the viscosity sense.}\end{align*} $$
$$ \begin{align*}\dfrac{S_{k}(D^{2}w)}{S_{l}(D^{2}w)}\geq f(x)~~\mbox{in}~\mathbb{R}^n~~~~\mbox{in the viscosity sense.}\end{align*} $$
Proof of Theorem 1.6
Without loss of generality, we may assume that
![]() $A=\mbox {diag}(a_{1},\ldots ,a_{n})\in \mathcal {A}_{k,l}$
,
$A=\mbox {diag}(a_{1},\ldots ,a_{n})\in \mathcal {A}_{k,l}$
,
![]() $0<a_1\leq a_2\leq \cdots \leq a_n$
and
$0<a_1\leq a_2\leq \cdots \leq a_n$
and
![]() $b=0$
.
$b=0$
.
For any
![]() $\delta> \sup _{r\in [1,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
, let
$\delta> \sup _{r\in [1,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
, let
where
![]() $r_{A}(x)$
is defined as in (1.12), where
$r_{A}(x)$
is defined as in (1.12), where
![]() $\rho _{\varsigma }(x)$
and
$\rho _{\varsigma }(x)$
and
![]() $h(r,\delta )$
are obtained from Lemmas 4.1 and 3.2, respectively, and
$h(r,\delta )$
are obtained from Lemmas 4.1 and 3.2, respectively, and
![]() $\kappa _1:=\min _{\substack {x\in \overline {E_{R}}\backslash \Omega \\ \varsigma \in \partial \Omega }}\rho _{\varsigma }(x)$
.
$\kappa _1:=\min _{\substack {x\in \overline {E_{R}}\backslash \Omega \\ \varsigma \in \partial \Omega }}\rho _{\varsigma }(x)$
.
Let
Since
![]() $\rho _{\varsigma }$
satisfies
$\rho _{\varsigma }$
satisfies
 $$ \begin{align*}\frac{S_k(D^2\rho_{\varsigma})}{S_l(D^2\rho_{\varsigma})}\geq g(x)\ \ \mbox{in}\ \ E_{2R},\end{align*} $$
$$ \begin{align*}\frac{S_k(D^2\rho_{\varsigma})}{S_l(D^2\rho_{\varsigma})}\geq g(x)\ \ \mbox{in}\ \ E_{2R},\end{align*} $$
then
![]() $\varphi $
satisfies
$\varphi $
satisfies
 $$ \begin{align}\frac{S_k(D^2\varphi)}{S_l(D^2\varphi)}\geq g(x)\ \ \mbox{in}\ \ E_{2R}~~~~\mbox{in the viscosity sense},\end{align} $$
$$ \begin{align}\frac{S_k(D^2\varphi)}{S_l(D^2\varphi)}\geq g(x)\ \ \mbox{in}\ \ E_{2R}~~~~\mbox{in the viscosity sense},\end{align} $$
and
By Theorem 3.4, we have that
![]() $W_{\delta }$
is a smooth k-convex subsolution of (1.1), i.e.,
$W_{\delta }$
is a smooth k-convex subsolution of (1.1), i.e.,
 $$ \begin{align} \frac{S_{k}(D^2W_{\delta})}{S_{l}(D^2W_{\delta})}\geq g(x)\ \mbox{in}\ \mathbb{R}^n\setminus\bar{\Omega}. \end{align} $$
$$ \begin{align} \frac{S_{k}(D^2W_{\delta})}{S_{l}(D^2W_{\delta})}\geq g(x)\ \mbox{in}\ \mathbb{R}^n\setminus\bar{\Omega}. \end{align} $$
Since
![]() $\Omega \subset \subset E_{R}$
, we can conclude that
$\Omega \subset \subset E_{R}$
, we can conclude that
Moreover, by Lemma 3.2,
![]() $W_{\delta }$
is strictly increasing in
$W_{\delta }$
is strictly increasing in
![]() $\delta $
and
$\delta $
and
By (3.12), we have that
 $$ \begin{align*}W_{\delta}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta+\mu(\delta)+\begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align*} $$
$$ \begin{align*}W_{\delta}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta+\mu(\delta)+\begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align*} $$
as
![]() $|x|\to +\infty $
, where
$|x|\to +\infty $
, where
Let
where
![]() $\kappa _2$
is any constant,
$\kappa _2$
is any constant,
![]() $\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(1)<\tau ^{k-l}<\underline {g}(1)$
and H is obtained from Lemma 3.5. Then we have that, by (3.35),
$\frac {\underline {t}_l}{\overline {t}_k}\underline {g}(1)<\tau ^{k-l}<\underline {g}(1)$
and H is obtained from Lemma 3.5. Then we have that, by (3.35),
 $$ \begin{align} \frac{S_k(D^2\overline{u}_{\kappa_2,\tau})}{S_l(D^2\overline{u}_{\kappa_2,\tau})}\leq g(x),\ \forall \ x\in \mathbb{R}^n\backslash \Omega, \end{align} $$
$$ \begin{align} \frac{S_k(D^2\overline{u}_{\kappa_2,\tau})}{S_l(D^2\overline{u}_{\kappa_2,\tau})}\leq g(x),\ \forall \ x\in \mathbb{R}^n\backslash \Omega, \end{align} $$
and by (3.34), as
![]() $|x|\to +\infty ,$
$|x|\to +\infty ,$
 $$ \begin{align*} \overline{u}_{\kappa_2,\tau}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +\nu_{\kappa_2}(\tau)+ \begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align*} $$
$$ \begin{align*} \overline{u}_{\kappa_2,\tau}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +\nu_{\kappa_2}(\tau)+ \begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}),\ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|),\ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align*} $$
where
is convergent.
Since
![]() $W_{\delta }$
is strictly increasing in
$W_{\delta }$
is strictly increasing in
![]() $\delta $
, then there exists some
$\delta $
, then there exists some
![]() $\hat {\delta }>\sup _{r\in [1,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
such that
$\hat {\delta }>\sup _{r\in [1,+\infty )} \overline {g}^{\frac {1}{k-l}}(r)$
such that
![]() $\min _{\partial E_{2R}}W_{\hat {\delta }}>\max _{\partial E_{2R}}\varphi $
. It follows that
$\min _{\partial E_{2R}}W_{\hat {\delta }}>\max _{\partial E_{2R}}\varphi $
. It follows that
Clearly,
![]() $\mu (\delta )$
is strictly increasing in
$\mu (\delta )$
is strictly increasing in
![]() $\delta $
. By (3.13), we have that
$\delta $
. By (3.13), we have that
![]() $\lim _{\delta \to +\infty }\mu (\delta )=+\infty $
.
$\lim _{\delta \to +\infty }\mu (\delta )=+\infty $
.
Let
 $$ \begin{align*}\hat{c}:=\hat{c}(\tau):=\sup_{E_{2R\backslash \Omega}}\varphi-\int_{0}^1\theta h_0(\theta)d\theta+\int_{1}^{+\infty}\theta[H(\theta)-h_0(\theta)]d\theta\end{align*} $$
$$ \begin{align*}\hat{c}:=\hat{c}(\tau):=\sup_{E_{2R\backslash \Omega}}\varphi-\int_{0}^1\theta h_0(\theta)d\theta+\int_{1}^{+\infty}\theta[H(\theta)-h_0(\theta)]d\theta\end{align*} $$
and
 $$ \begin{align*}\tilde{c}:=\max\{\hat{c},\mu(\hat{\delta}),\max_{\substack{\varsigma\in \partial\Omega\\x\in \overline{E_{2R}}\backslash\Omega}}\rho_{\varsigma}(x)\}.\end{align*} $$
$$ \begin{align*}\tilde{c}:=\max\{\hat{c},\mu(\hat{\delta}),\max_{\substack{\varsigma\in \partial\Omega\\x\in \overline{E_{2R}}\backslash\Omega}}\rho_{\varsigma}(x)\}.\end{align*} $$
Then, for any
![]() $c>\tilde {c}$
, there is a unique
$c>\tilde {c}$
, there is a unique
![]() $\delta (c)$
such that
$\delta (c)$
such that
![]() $\mu (\delta (c))=c.$
Consequently, we have that
$\mu (\delta (c))=c.$
Consequently, we have that
 $$ \begin{align} W_{\delta(c)}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +c+ \begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|), \ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align} $$
$$ \begin{align} W_{\delta(c)}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +c+ \begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|), \ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align} $$
as
![]() $|x|\to +\infty $
, and
$|x|\to +\infty $
, and
By the monotonicity of
![]() $W_{\delta }$
in
$W_{\delta }$
in
![]() $\delta $
and (4.6), we conclude that
$\delta $
and (4.6), we conclude that
Taking
![]() $\kappa _{2}$
such that
$\kappa _{2}$
such that
![]() $\nu _{\kappa _2}(\tau )=c$
. Then we have that
$\nu _{\kappa _2}(\tau )=c$
. Then we have that
and as
![]() $|x|\to +\infty $
,
$|x|\to +\infty $
,
 $$ \begin{align} \overline{u}_{\kappa_2,\tau}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +c+\begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|), \ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}. \end{cases} \end{align} $$
$$ \begin{align} \overline{u}_{\kappa_2,\tau}(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +c+\begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|), \ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}. \end{cases} \end{align} $$
Define
 $$ \begin{align*}\underline{u}(x):= \begin{cases} \max\{W_{\delta(c)}(x),\varphi(x)\},&x\in E_{2R}\backslash\Omega,\\ W_{\delta(c)}(x),&x\in \mathbb{R}^n\backslash E_{2R}. \end{cases}\end{align*} $$
$$ \begin{align*}\underline{u}(x):= \begin{cases} \max\{W_{\delta(c)}(x),\varphi(x)\},&x\in E_{2R}\backslash\Omega,\\ W_{\delta(c)}(x),&x\in \mathbb{R}^n\backslash E_{2R}. \end{cases}\end{align*} $$
Then, by (4.8), we have that
![]() $\underline {u}\in C^0(\mathbb {R}^n\backslash \Omega )$
. By (4.1), (4.3), and Lemma 4.3,
$\underline {u}\in C^0(\mathbb {R}^n\backslash \Omega )$
. By (4.1), (4.3), and Lemma 4.3,
![]() $\underline {u}$
satisfies in the viscosity sense
$\underline {u}$
satisfies in the viscosity sense
 $$ \begin{align*}\dfrac{S_{k}(D^2\underline{u})}{S_{l}(D^2\underline{u})}\geq g(x)\ \ \mbox{in}\ \ \mathbb{R}^n\backslash\overline{\Omega}.\end{align*} $$
$$ \begin{align*}\dfrac{S_{k}(D^2\underline{u})}{S_{l}(D^2\underline{u})}\geq g(x)\ \ \mbox{in}\ \ \mathbb{R}^n\backslash\overline{\Omega}.\end{align*} $$
By (4.4) and (4.2), we obtain that
![]() $\underline {u}=\phi $
on
$\underline {u}=\phi $
on
![]() $\partial \Omega $
. Moreover, by (4.7), we have that
$\partial \Omega $
. Moreover, by (4.7), we have that
![]() $\underline {u}$
satisfies the asymptotic behavior (4.10) at infinity.
$\underline {u}$
satisfies the asymptotic behavior (4.10) at infinity.
By the definitions of
![]() $\tilde {c}$
,
$\tilde {c}$
,
![]() $\overline {u}_{\kappa _2}$
, and
$\overline {u}_{\kappa _2}$
, and
![]() $\varphi $
, we have that
$\varphi $
, we have that
By (4.4),
![]() $W_{\delta (c)}\leq \varphi \leq \overline {u}_{\kappa _2,\tau }$
on
$W_{\delta (c)}\leq \varphi \leq \overline {u}_{\kappa _2,\tau }$
on
![]() $\partial \Omega $
. By (4.3), (4.5), (4.7), (4.10), and the comparison principle, we have that
$\partial \Omega $
. By (4.3), (4.5), (4.7), (4.10), and the comparison principle, we have that
Let
![]() $\overline {u}:=\overline {u}_{\kappa _2,\tau }$
in
$\overline {u}:=\overline {u}_{\kappa _2,\tau }$
in
![]() $\mathbb {R}^n\backslash \Omega $
. By (4.11), (4.12), and the definition of
$\mathbb {R}^n\backslash \Omega $
. By (4.11), (4.12), and the definition of
![]() $\underline {u}$
, we have that
$\underline {u}$
, we have that
![]() $\underline {u}\leq \overline {u}$
in
$\underline {u}\leq \overline {u}$
in
![]() $\mathbb {R}^n\backslash \Omega $
.
$\mathbb {R}^n\backslash \Omega $
.
For any
![]() $c>\tilde {c}$
, let
$c>\tilde {c}$
, let
![]() $\mathcal {S}_c$
denote the set of
$\mathcal {S}_c$
denote the set of
![]() $\varrho \in C^0(\mathbb {R}^n\backslash \Omega )$
which are viscosity subsolutions of (1.1) and (1.2) satisfying
$\varrho \in C^0(\mathbb {R}^n\backslash \Omega )$
which are viscosity subsolutions of (1.1) and (1.2) satisfying
![]() $\varrho =\phi $
on
$\varrho =\phi $
on
![]() $\partial \Omega $
and
$\partial \Omega $
and
![]() $\varrho \leq \overline {u}$
in
$\varrho \leq \overline {u}$
in
![]() $\mathbb {R}^n\backslash \Omega $
. Apparently,
$\mathbb {R}^n\backslash \Omega $
. Apparently,
![]() $\underline {u}\in \mathcal {S}_c$
, which implies that
$\underline {u}\in \mathcal {S}_c$
, which implies that
![]() $\mathcal {S}_c\neq \emptyset .$
Define
$\mathcal {S}_c\neq \emptyset .$
Define
Then
Hence, by the asymptotic behavior of
![]() $\underline {u}$
and
$\underline {u}$
and
![]() $\overline {u}$
at infinity, we have that
$\overline {u}$
at infinity, we have that
 $$ \begin{align*} u(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +c+\begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|), \ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align*} $$
$$ \begin{align*} u(x)=\displaystyle\int_{0}^{r_A(x)}\theta h_0(\theta)d\theta +c+\begin{cases} O(|x|^{2-\min\{\beta,\frac{k-l}{\overline{t}_k-\underline{t}_l}\}}), \ \mbox{if} \ \beta\not=\frac{k-l}{\overline{t}_k-\underline{t}_l},\\ O(|x|^{2-\frac{k-l}{\overline{t}_k-\underline{t}_l}}\ln |x|), \ \mbox{if} \ \beta=\frac{k-l}{\overline{t}_k-\underline{t}_l}, \end{cases} \end{align*} $$
as
![]() $|x|\to +\infty $
.
$|x|\to +\infty $
.
Next, we will show that
![]() $u=\phi $
on
$u=\phi $
on
![]() $\partial \Omega .$
On one side, since
$\partial \Omega .$
On one side, since
![]() $\underline {u}=\phi $
on
$\underline {u}=\phi $
on
![]() $\partial \Omega ,$
we have that
$\partial \Omega ,$
we have that
On the other side, we want to prove that
Let
![]() $\vartheta \in C^2(\overline {E_{2R}\backslash \Omega })$
satisfy
$\vartheta \in C^2(\overline {E_{2R}\backslash \Omega })$
satisfy
 $$ \begin{align*}\begin{cases} \Delta \vartheta=0,&\ \mbox{in}\ E_{2R}\backslash\bar{\Omega},\\ \vartheta=\phi,&\ \mbox{on}\ \partial\Omega,\\ \vartheta=\max_{\partial E_{2R}}\overline{u},&\ \mbox{on}\ \partial E_{2R}. \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \Delta \vartheta=0,&\ \mbox{in}\ E_{2R}\backslash\bar{\Omega},\\ \vartheta=\phi,&\ \mbox{on}\ \partial\Omega,\\ \vartheta=\max_{\partial E_{2R}}\overline{u},&\ \mbox{on}\ \partial E_{2R}. \end{cases}\end{align*} $$
By Newton’s inequality, for any
![]() $\varrho \in \mathcal {S}_c$
, we have that
$\varrho \in \mathcal {S}_c$
, we have that
![]() $\Delta \varrho \geq 0$
in the viscosity sense. Moreover,
$\Delta \varrho \geq 0$
in the viscosity sense. Moreover,
![]() $\varrho \leq \vartheta $
on
$\varrho \leq \vartheta $
on
![]() $\partial (E_{2R}\backslash \Omega )$
. Then, by the comparison principle, we have that
$\partial (E_{2R}\backslash \Omega )$
. Then, by the comparison principle, we have that
![]() $\varrho \leq \vartheta \ \ \mbox {in}\ \ E_{2R}\backslash \Omega $
. It follows that
$\varrho \leq \vartheta \ \ \mbox {in}\ \ E_{2R}\backslash \Omega $
. It follows that
![]() $u\leq \vartheta \ \ \mbox {in}\ \ E_{2R}\backslash \Omega $
. Therefore,
$u\leq \vartheta \ \ \mbox {in}\ \ E_{2R}\backslash \Omega $
. Therefore,
Finally, we will prove that
![]() $u\in C^0(\mathbb {R}^n\backslash \Omega )$
is a viscosity solution of (1.1). For any
$u\in C^0(\mathbb {R}^n\backslash \Omega )$
is a viscosity solution of (1.1). For any
![]() $x\in \mathbb {R}^n\backslash \overline {\Omega },$
choose some
$x\in \mathbb {R}^n\backslash \overline {\Omega },$
choose some
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $B_{\varepsilon }=B_{\varepsilon }(x)\subset \mathbb {R}^n\backslash \overline {\Omega }.$
By Lemma 4.2, the following Dirichlet problem
$B_{\varepsilon }=B_{\varepsilon }(x)\subset \mathbb {R}^n\backslash \overline {\Omega }.$
By Lemma 4.2, the following Dirichlet problem
 $$ \begin{align} \begin{cases} \dfrac{S_k(D^2\tilde{u})}{S_l(D^2\tilde{u})}=g(y),&\mbox{in}\ B_{\varepsilon},\\ \tilde{u}=u, &\mbox{on}\ \partial B_{\varepsilon} \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \dfrac{S_k(D^2\tilde{u})}{S_l(D^2\tilde{u})}=g(y),&\mbox{in}\ B_{\varepsilon},\\ \tilde{u}=u, &\mbox{on}\ \partial B_{\varepsilon} \end{cases} \end{align} $$
admits a unique k-convex viscosity solution
![]() $\tilde {u}\in C^0(\overline {B_{\varepsilon }}).$
By the comparison principle,
$\tilde {u}\in C^0(\overline {B_{\varepsilon }}).$
By the comparison principle,
![]() $u\leq \tilde {u}$
in
$u\leq \tilde {u}$
in
![]() $B_{\varepsilon }$
. Define
$B_{\varepsilon }$
. Define
 $$ \begin{align*}\tilde{w}(y)= \begin{cases} \tilde{u}(y),&\ \mbox{in}\ B_{\varepsilon},\\ u(y),&\ \mbox{in}\ (\mathbb{R}^n\backslash\Omega) \backslash B_{\varepsilon}. \end{cases} \end{align*} $$
$$ \begin{align*}\tilde{w}(y)= \begin{cases} \tilde{u}(y),&\ \mbox{in}\ B_{\varepsilon},\\ u(y),&\ \mbox{in}\ (\mathbb{R}^n\backslash\Omega) \backslash B_{\varepsilon}. \end{cases} \end{align*} $$
Then
![]() $\tilde {w}\in \mathcal {S}_{c}.$
Indeed, by the comparison principle,
$\tilde {w}\in \mathcal {S}_{c}.$
Indeed, by the comparison principle,
![]() $\tilde {u}(y)\leq \overline {u}(y)$
in
$\tilde {u}(y)\leq \overline {u}(y)$
in
![]() $\bar {B}_{\varepsilon }$
. It follows that
$\bar {B}_{\varepsilon }$
. It follows that
![]() $\tilde {w}\leq \overline {u}$
in
$\tilde {w}\leq \overline {u}$
in
![]() $\mathbb {R}^n\backslash B_{\varepsilon }.$
By Lemma 4.3, we have that
$\mathbb {R}^n\backslash B_{\varepsilon }.$
By Lemma 4.3, we have that
![]() $\frac {S_k(D^2\tilde {w})}{S_l(D^2\tilde {w})}\geq g(y)$
in
$\frac {S_k(D^2\tilde {w})}{S_l(D^2\tilde {w})}\geq g(y)$
in
![]() $\mathbb {R}^n\backslash \overline {\Omega }$
in the viscosity sense. Therefore,
$\mathbb {R}^n\backslash \overline {\Omega }$
in the viscosity sense. Therefore,
![]() $\tilde {w}\in \mathcal {S}_{c}.$
$\tilde {w}\in \mathcal {S}_{c}.$
By the definition of u,
![]() $u\geq \tilde {w}$
in
$u\geq \tilde {w}$
in
![]() $\mathbb {R}^n\backslash \Omega $
. It follows that
$\mathbb {R}^n\backslash \Omega $
. It follows that
![]() $u\geq \tilde {u}$
in
$u\geq \tilde {u}$
in
![]() $B_{\varepsilon }.$
Hence,
$B_{\varepsilon }.$
Hence,
![]() $u\equiv \tilde {u}$
in
$u\equiv \tilde {u}$
in
![]() $B_{\varepsilon }$
. Since
$B_{\varepsilon }$
. Since
![]() $\tilde {u}$
satisfies (4.13), then we have that in the viscosity sense,
$\tilde {u}$
satisfies (4.13), then we have that in the viscosity sense,
 $$ \begin{align*}\dfrac{S_k(D^2u)}{S_l(D^2u)}=g(y),~\forall~y\in B_{\varepsilon}.\end{align*} $$
$$ \begin{align*}\dfrac{S_k(D^2u)}{S_l(D^2u)}=g(y),~\forall~y\in B_{\varepsilon}.\end{align*} $$
In particular, we have that in the viscosity sense,
 $$ \begin{align*}\dfrac{S_k(D^2u)}{S_l(D^2u)}=g(x).\end{align*} $$
$$ \begin{align*}\dfrac{S_k(D^2u)}{S_l(D^2u)}=g(x).\end{align*} $$
Since x is arbitrary, we can conclude that u is a viscosity solution of (1.1).
Theorem 1.6 is proved.
A Appendix
In this appendix, we will show that it is impossible to construct the generalized symmetric solution of (3.3).
Proposition A.1 If there exists a
![]() $C^{2}$
function defined on
$C^{2}$
function defined on
![]() $(r_{1},r_{2})$
such that
$(r_{1},r_{2})$
such that
![]() $T(x):=G(r)$
is a generalized symmetric solution of (3.3), then
$T(x):=G(r)$
is a generalized symmetric solution of (3.3), then
 $$ \begin{align*}k=n,\ \ \mbox{or}\ \ a_1=\cdots=a_n=\hat{a}=\left(\binom{n}{l}/\binom{n}{k}\right)^{\frac{1}{k-l}},\end{align*} $$
$$ \begin{align*}k=n,\ \ \mbox{or}\ \ a_1=\cdots=a_n=\hat{a}=\left(\binom{n}{l}/\binom{n}{k}\right)^{\frac{1}{k-l}},\end{align*} $$
where
![]() $r=r_{A}$
is defined as in (1.12).
$r=r_{A}$
is defined as in (1.12).
Before proving the above proposition, we will first give some elementary lemmas.
Lemma A.2 If
![]() $M=(p_i\delta _{ij}+sq_iq_j)_{n\times n}$
with
$M=(p_i\delta _{ij}+sq_iq_j)_{n\times n}$
with
![]() $p,q\in \mathbb {R}^n$
and
$p,q\in \mathbb {R}^n$
and
![]() $s\in \mathbb {R}$
, then
$s\in \mathbb {R}$
, then
 $$ \begin{align*}\sigma_k(\lambda(M))=\sigma_k(p)+s\sum_{i=1}^n\sigma_{k-1;i}(p)q_i^2,~k=1,\dots,n.\end{align*} $$
$$ \begin{align*}\sigma_k(\lambda(M))=\sigma_k(p)+s\sum_{i=1}^n\sigma_{k-1;i}(p)q_i^2,~k=1,\dots,n.\end{align*} $$
Proof See [Reference Bao, Li and Li2].
Lemma A.3 Suppose that
![]() $\tilde {\phi }\in C^2[0,+\infty )$
and
$\tilde {\phi }\in C^2[0,+\infty )$
and
![]() $\tilde {\Phi }(x):=\tilde {\phi }(r)$
. Then
$\tilde {\Phi }(x):=\tilde {\phi }(r)$
. Then
![]() $\tilde {\Phi }$
satisfies
$\tilde {\Phi }$
satisfies
 $$ \begin{align} S_k(D^2\tilde{\Phi})=\sigma_k(a)\tilde{h}(r)^k+\frac{\tilde{h}'(r)}{r} \tilde{h}(r)^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2, \end{align} $$
$$ \begin{align} S_k(D^2\tilde{\Phi})=\sigma_k(a)\tilde{h}(r)^k+\frac{\tilde{h}'(r)}{r} \tilde{h}(r)^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2, \end{align} $$
where
![]() $\tilde {h}(r):=\tilde {\phi }^{\prime }(r)/r$
.
$\tilde {h}(r):=\tilde {\phi }^{\prime }(r)/r$
.
Proof Since
![]() $r^2=x^{T}Ax=\sum _{i=1}^na_ix_i^2,$
we have that
$r^2=x^{T}Ax=\sum _{i=1}^na_ix_i^2,$
we have that
It follows that
 $$ \begin{align*} \partial_{x_i}\tilde{\Phi}(x)&=\tilde{\phi}'(r)\partial_{x_i}r=\frac{\tilde{\phi}'(r)}{r}a_ix_i,\\ \partial_{x_ix_j}\tilde{\Phi}(x)&=\frac{\tilde{\phi}'(r)}{r}a_i\delta_{ij}+\frac{\tilde{\phi}"(r)-\frac{\tilde{\phi}'(r)}{r}}{r^2}(a_ix_i)(a_jx_j)\\ &=\tilde{h}(r)a_i\delta_{ij}+\frac{\tilde{h}'(r)}{r}(a_ix_i)(a_jx_j). \end{align*} $$
$$ \begin{align*} \partial_{x_i}\tilde{\Phi}(x)&=\tilde{\phi}'(r)\partial_{x_i}r=\frac{\tilde{\phi}'(r)}{r}a_ix_i,\\ \partial_{x_ix_j}\tilde{\Phi}(x)&=\frac{\tilde{\phi}'(r)}{r}a_i\delta_{ij}+\frac{\tilde{\phi}"(r)-\frac{\tilde{\phi}'(r)}{r}}{r^2}(a_ix_i)(a_jx_j)\\ &=\tilde{h}(r)a_i\delta_{ij}+\frac{\tilde{h}'(r)}{r}(a_ix_i)(a_jx_j). \end{align*} $$
By Lemma A.2, we have that
 $$ \begin{align*} S_k(D^2\tilde{\Phi})&=\sigma_k(\lambda(D^2\tilde{\Phi}))\nonumber\\ &=\sigma_k(a)\tilde{h}(r)^k+\frac{\tilde{h}'(r)}{r}\tilde{h}(r)^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2.\\[-41pt] \end{align*} $$
$$ \begin{align*} S_k(D^2\tilde{\Phi})&=\sigma_k(\lambda(D^2\tilde{\Phi}))\nonumber\\ &=\sigma_k(a)\tilde{h}(r)^k+\frac{\tilde{h}'(r)}{r}\tilde{h}(r)^{k-1}\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2.\\[-41pt] \end{align*} $$
Lemma A.4 Let
![]() $a=(a_1,a_2,\dots ,a_n)$
satisfy
$a=(a_1,a_2,\dots ,a_n)$
satisfy
![]() $0<a_1\leq a_2\leq \dots \leq a_n.$
Then, for
$0<a_1\leq a_2\leq \dots \leq a_n.$
Then, for
![]() $1\leq k\leq n$
,
$1\leq k\leq n$
,
and
where
![]() $\underline {t}_k$
and
$\underline {t}_k$
and
![]() $\overline {t}_{k}$
are defined as in (1.4) and (1.5). Moreover, for
$\overline {t}_{k}$
are defined as in (1.4) and (1.5). Moreover, for
![]() $1\leq k\leq n-1,$
$1\leq k\leq n-1,$
if and only if
![]() $a_{1}=\cdots =a_{n}=\overline {C}$
for some
$a_{1}=\cdots =a_{n}=\overline {C}$
for some
![]() $\overline {C}>0$
.
$\overline {C}>0$
.
Remark A.5 From (A.2), we know that
Then
Now we give the proof of Proposition A.1.
Proof For the special case
![]() $l=0,1\leq k\leq n$
, the Hessian equation case, Proposition A.1 can be proved similarly with Proposition 2.2 in [Reference Cao and Bao9]. We only need to prove the case
$l=0,1\leq k\leq n$
, the Hessian equation case, Proposition A.1 can be proved similarly with Proposition 2.2 in [Reference Cao and Bao9]. We only need to prove the case
![]() $1\leq l<k\leq n$
.
$1\leq l<k\leq n$
.
Let
![]() $J(r)=G^{\prime }(r)/r$
. By (A.1), we know that T satisfies
$J(r)=G^{\prime }(r)/r$
. By (A.1), we know that T satisfies
 $$ \begin{align*} \frac{S_k(D^2T)}{S_l(D^2T)}=\frac{\sigma_k(a)J(r)^k+\frac{J'(r)}{r}J(r)^{k-1}\displaystyle\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2} {\sigma_l(a)J(r)^l+\frac{J'(r)}{r}J(r)^{l-1}\displaystyle\sum_{i=1}^{n}\sigma_{l-1;i}(a)a_i^2x_i^2}=\overline{g}(r). \end{align*} $$
$$ \begin{align*} \frac{S_k(D^2T)}{S_l(D^2T)}=\frac{\sigma_k(a)J(r)^k+\frac{J'(r)}{r}J(r)^{k-1}\displaystyle\sum_{i=1}^{n}\sigma_{k-1;i}(a)a_i^2x_i^2} {\sigma_l(a)J(r)^l+\frac{J'(r)}{r}J(r)^{l-1}\displaystyle\sum_{i=1}^{n}\sigma_{l-1;i}(a)a_i^2x_i^2}=\overline{g}(r). \end{align*} $$
Set
![]() $x=(0,\dots ,0,\sqrt {r/a_i},0,\dots ,0)$
. Then
$x=(0,\dots ,0,\sqrt {r/a_i},0,\dots ,0)$
. Then
 $$ \begin{align*} \frac{S_k(D^2T)}{S_l(D^2T)}=\frac{\sigma_k(a)J(r)^k+J'(r)J(r)^{k-1}\sigma_{k-1;i}(a)a_i} {\sigma_l(a)J(r)^l+J'(r)J(r)^{l-1}\sigma_{l-1;i}(a)a_i}=\overline{g}(r). \end{align*} $$
$$ \begin{align*} \frac{S_k(D^2T)}{S_l(D^2T)}=\frac{\sigma_k(a)J(r)^k+J'(r)J(r)^{k-1}\sigma_{k-1;i}(a)a_i} {\sigma_l(a)J(r)^l+J'(r)J(r)^{l-1}\sigma_{l-1;i}(a)a_i}=\overline{g}(r). \end{align*} $$
So
Since
![]() $\sigma _k(a)=\sigma _l(a)$
, then
$\sigma _k(a)=\sigma _l(a)$
, then
 $$ \begin{align} \frac{J(r)^k-\overline{g}(r)J(r)^l}{J^{\prime}(r)}=\frac{\overline{g}(r)J(r)^{l-1}\sigma_{l-1;i}(a)a_i-J(r)^{k-1}\sigma_{k-1;i}(a)a_i}{\sigma_k(a)}.\end{align} $$
$$ \begin{align} \frac{J(r)^k-\overline{g}(r)J(r)^l}{J^{\prime}(r)}=\frac{\overline{g}(r)J(r)^{l-1}\sigma_{l-1;i}(a)a_i-J(r)^{k-1}\sigma_{k-1;i}(a)a_i}{\sigma_k(a)}.\end{align} $$
Noting that the left side of (A.4) is independent of i, so for any
![]() $i\not =j,$
we have that
$i\not =j,$
we have that
As a result,
Applying the equality
![]() $\sigma _k(a)=\sigma _{k;i}(a)+a_i\sigma _{k-1;i}(a)$
for all
$\sigma _k(a)=\sigma _{k;i}(a)+a_i\sigma _{k-1;i}(a)$
for all
![]() $i,$
we get that
$i,$
we get that
 $$ \begin{align*}&\sigma_{l-1;i}(a)a_i-\sigma_{l-1;j}(a)a_j\\ &\quad=[\sigma_{l-1;ij}(a)+\sigma_{l-2;ij}(a)a_j]a_i-[\sigma_{l-1;ij}(a)+\sigma_{l-2;ij}(a)a_i]a_j\\ &\quad=\sigma_{l-1;ij}(a)(a_i-a_j). \end{align*} $$
$$ \begin{align*}&\sigma_{l-1;i}(a)a_i-\sigma_{l-1;j}(a)a_j\\ &\quad=[\sigma_{l-1;ij}(a)+\sigma_{l-2;ij}(a)a_j]a_i-[\sigma_{l-1;ij}(a)+\sigma_{l-2;ij}(a)a_i]a_j\\ &\quad=\sigma_{l-1;ij}(a)(a_i-a_j). \end{align*} $$
Therefore, (A.5) becomes
If
![]() $k=n$
, then
$k=n$
, then
![]() $\sigma _{k-1;ij}(a)=0$
for any
$\sigma _{k-1;ij}(a)=0$
for any
![]() $i\not =j$
. But
$i\not =j$
. But
![]() $\sigma _{l-1;ij}(a)>0$
, so we get that
$\sigma _{l-1;ij}(a)>0$
, so we get that
If
![]() $1\leq l<k\leq n-1$
, then
$1\leq l<k\leq n-1$
, then
![]() $\sigma _{k-1;ij}(a)>0$
and
$\sigma _{k-1;ij}(a)>0$
and
![]() $\sigma _{l-1;ij}(a)>0$
. Suppose on the contrary that
$\sigma _{l-1;ij}(a)>0$
. Suppose on the contrary that
![]() $a_i\not =a_j$
, then
$a_i\not =a_j$
, then
Thus,
 $$ \begin{align} \frac{\sigma_{k-1;ij}(a)}{\sigma_{l-1;ij}(a)}= \frac{\overline{g}(r)J(r)^{l-1}}{J(r)^{k-1}}=\overline{g}(r)J(r)^{l-k}. \end{align} $$
$$ \begin{align} \frac{\sigma_{k-1;ij}(a)}{\sigma_{l-1;ij}(a)}= \frac{\overline{g}(r)J(r)^{l-1}}{J(r)^{k-1}}=\overline{g}(r)J(r)^{l-k}. \end{align} $$
Since the left side is independent of r, then
![]() $\overline {g}(r)J(r)^{l-k}$
is a constant
$\overline {g}(r)J(r)^{l-k}$
is a constant
![]() $c_0>0.$
So
$c_0>0.$
So
![]() $\overline {g}(r)=c_0J(r)^{k-l}.$
Substituting into (A.4), we have that
$\overline {g}(r)=c_0J(r)^{k-l}.$
Substituting into (A.4), we have that
 $$ \begin{align}\frac{J(r)(1-c_0)}{c_0J^{\prime}(r)}=\frac{\sigma_{l-1;i}(a)a_i-\sigma_{k-1;i}(a)a_i}{\sigma_k(a)}.\end{align} $$
$$ \begin{align}\frac{J(r)(1-c_0)}{c_0J^{\prime}(r)}=\frac{\sigma_{l-1;i}(a)a_i-\sigma_{k-1;i}(a)a_i}{\sigma_k(a)}.\end{align} $$
Since the left side of the above equality is independent of i, then for any
![]() $i\not =j$
,
$i\not =j$
,
so
However,
![]() $a_i\not =a_j$
; thus,
$a_i\not =a_j$
; thus,
![]() $\sigma _{l-1;ij}(a)=\sigma _{k-1;ij}(a)$
. Therefore, by (A.6), we can have
$\sigma _{l-1;ij}(a)=\sigma _{k-1;ij}(a)$
. Therefore, by (A.6), we can have
![]() $c_0=1$
. Then, by (A.7), we can get that for all i,
$c_0=1$
. Then, by (A.7), we can get that for all i,
Recalling the equality
 $$ \begin{align*}\sum_{i=1}^{n}a_i\sigma_{k-1;i}(a)=k\sigma_k(a),\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{n}a_i\sigma_{k-1;i}(a)=k\sigma_k(a),\end{align*} $$
we know that
![]() $k\sigma _k(a)=l\sigma _l(a)$
. Since
$k\sigma _k(a)=l\sigma _l(a)$
. Since
![]() $A\in \mathcal {A}_{k,l}$
, we can conclude that
$A\in \mathcal {A}_{k,l}$
, we can conclude that
![]() $\sigma _k(a)=\sigma _l(a)$
and
$\sigma _k(a)=\sigma _l(a)$
and
![]() $k=l$
, which is a contradiction.
$k=l$
, which is a contradiction.