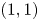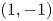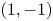1. Introduction
Wendelstein-type stellarators greatly reduce prompt losses of trapped energetic particles by employing quasi-isodynamic magnetic configurations: when the ratio of plasma pressure to magnetic field pressure is sufficiently high, diamagnetic drift of fast ions compensates for their radial magnetic drift averaged over the orbit. This suppresses losses on the drift time scale resulting from trapped particles’ drift orbits intersecting the plasma boundary. Nevertheless, numerical modelling shows that a significant fraction of trapped energetic particles suffer delayed losses (Lotz et al. Reference Lotz, Merkel, Nührenberg and Strumberger1992; Drevlak et al. Reference Drevlak, Geiger, Helander and Turkin2014). These delayed losses, which occur on timescales much larger than the drift timescale, have been theorised to occur due to stochastic diffusion (Beidler et al. Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001; Tykhyy Reference Tykhyy2018), as particles drifting between magnetic field lines repeatedly become trapped in or escape from local magnetic wells associated with the mirror harmonic of the magnetic field; this hypothesis has recently been corroborated by numerical simulations following orbits of individual particles over an extended period (Kolesnichenko, Lutsenko & Tykhyy Reference Kolesnichenko, Lutsenko and Tykhyy2022). Note that stellarator-based reactor designs assume high alpha heating efficiencies: 90 % or even 95 % (see, e.g., Sagara, Igitkhanov & Najmabadi Reference Sagara, Igitkhanov and Najmabadi2010). In addition, alpha particle losses tend to be spatially localised on the first wall and can create very high-energy fluxes and wall damage even if the great majority of alpha particles are confined. This means that even though the fraction of such transitioning fast ions may be small, their confinement properties are important.
Some of the approaches which have been suggested to deal with the delayed losses of these transitioning particles, such as modification of the mirror harmonic (Tykhyy et al. Reference Tykhyy, Kolesnichenko, Yakovenko, Weller and Werner2007), control of radial electric field (Tykhyy et al. Reference Tykhyy, Kolesnichenko, Yakovenko, Weller and Werner2007; Tykhyy & Kolesnichenko Reference Tykhyy and Kolesnichenko2021), rely on controlling the shape of the separatrix between two types of trapped particle orbits: those trapped in local magnetic wells and those trapped by the toroidal inhomogeneity of the magnetic field. However, there are difficulties involved in these approaches, as, e.g., the radial electric field in stellarators arises due to the neoclassical fluxes and may not be readily modified to suit the requirements of separatrix control for energetic particle loss mitigation.
Another approach relies on numerical optimisation of the stellarator magnetic field structure to eliminate transitioning particles. Recent papers from some of the groups pursuing this approach include Landreman & Paul (Reference Landreman and Paul2022), Sanchez et al. (Reference Sanchez, Velasco, Calvo and Mulas2023) and Bindel, Landreman & Padidar (Reference Bindel, Landreman and Padidar2023). It adds relatively easy-to-compute performance metrics related to trapped energetic particle behaviour to a set of other optimisation criteria, such as low bootstrap current, effective ripple and magnetic well. Direct modelling of energetic particle losses by orbit following in a given configuration can be performed in the main optimisation loop (Bindel et al. Reference Bindel, Landreman and Padidar2023), but it is computationally expensive, and is more often performed at intervals in the optimisation process as a check on the indirect performance metrics. Albert et al. (Reference Albert, Buchholz, Kasilov, Kernbichler and Rath2023) offers a more computationally efficient approach based on orbit classification using a sample of energetic particle orbits which need to be numerically followed for much shorter periods than is required by direct modelling. After a desirable magnetic configuration is achieved, a separate optimisation process can then be used to compute the coil set generating it; usually single-filament coils are generated to illustrate approximately how the coil set would look. The initial optimisation can produce magnetic configurations with very good energetic particle confinement properties, such as those given by Sanchez et al. (Reference Sanchez, Velasco, Calvo and Mulas2023), Bindel et al. (Reference Bindel, Landreman and Padidar2023) and Bader et al. (Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021). However, the resulting coils are complicated and it is unclear if they can be constructed economically. Even single-filament coils do not reproduce the desired magnetic configuration exactly, leading to degraded confinement, and one may expect that this problem will be exacerbated with realistic coils. In addition, the metrics which are used to optimise the configuration do not have a simple relationship to energetic particle loss fraction, which is the really important metric. Numerical modelling with orbit-following codes shows that configurations which are worse on the optimisation metrics can confine particles as well or better than those which are better on optimisation metrics, and vice versa (Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021). This underscores the need for a physical understanding of the long-term behaviour of trapped energetic particles.
A simpler approach to reducing particle losses (Beidler & Maasberg Reference Beidler and Maasberg2001) is to increase the $(1, -1)$![]() harmonic of the magnetic field, which is small in regular Wendelstein-type configurations. This modification of the magnetic configuration increases its omnigeneity (Helander Reference Helander2014), improving trapped particle confinement and at the same time decreasing bootstrap current (Gori, Lotz & Nuhrenberg Reference Gori, Lotz and Nuhrenberg1994; Helander & Nuhrenberg Reference Helander and Nuhrenberg2009; Helander, Geiger & Maasberg Reference Helander, Geiger and Maasberg2011). The purpose of this work is to examine the effect of this modification on transitioning particles and its implications for stochastic diffusion losses.
harmonic of the magnetic field, which is small in regular Wendelstein-type configurations. This modification of the magnetic configuration increases its omnigeneity (Helander Reference Helander2014), improving trapped particle confinement and at the same time decreasing bootstrap current (Gori, Lotz & Nuhrenberg Reference Gori, Lotz and Nuhrenberg1994; Helander & Nuhrenberg Reference Helander and Nuhrenberg2009; Helander, Geiger & Maasberg Reference Helander, Geiger and Maasberg2011). The purpose of this work is to examine the effect of this modification on transitioning particles and its implications for stochastic diffusion losses.
The structure of this work is as follows. In § 2, the theory of transitioning particles of Beidler et al. (Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001), Tykhyy (Reference Tykhyy2018) and Kolesnichenko et al. (Reference Kolesnichenko, Lutsenko and Tykhyy2022) is extended to include a bi-helical magnetic harmonic, and simple analytical expressions describing separatrix properties are derived. In § 3, the behaviour of drift particle orbits and the separatrix in a Wendelstein-type magnetic configuration with an enhanced bi-helical harmonic is examined numerically. Section 4 summarises the results obtained.
2. Analytical consideration
We take magnetic field strength in the form
in flux coordinates $r$![]() , $\vartheta$
, $\vartheta$![]() and $\varphi$
and $\varphi$![]() ; the radial coordinate $r$
; the radial coordinate $r$![]() is defined by $\psi =\bar {B}r^2/2$
is defined by $\psi =\bar {B}r^2/2$![]() , $\psi$
, $\psi$![]() is the toroidal magnetic flux, $\vartheta$
is the toroidal magnetic flux, $\vartheta$![]() and $\varphi$
and $\varphi$![]() are the poloidal and toroidal angles. Here, $\bar {B}$
are the poloidal and toroidal angles. Here, $\bar {B}$![]() is the average magnetic field at the magnetic axis, $\epsilon _{\rm h}>0$
is the average magnetic field at the magnetic axis, $\epsilon _{\rm h}>0$![]() , $\epsilon _{\rm H}>0$
, $\epsilon _{\rm H}>0$![]() , $\epsilon _{\rm m}>0$
, $\epsilon _{\rm m}>0$![]() , $\epsilon _{\rm t}>0$
, $\epsilon _{\rm t}>0$![]() and $\epsilon ^{(0)}>0$
and $\epsilon ^{(0)}>0$![]() are the amplitudes of the helical $(1,1)$
are the amplitudes of the helical $(1,1)$![]() and $(1, -1)$
and $(1, -1)$![]() , mirror $(0,1)$
, mirror $(0,1)$![]() , toroidal $(1,0)$
, toroidal $(1,0)$![]() and diamagnetic $(0,0)$
and diamagnetic $(0,0)$![]() Fourier harmonics of $B$
Fourier harmonics of $B$![]() , respectively; these amplitudes are $o(1)$
, respectively; these amplitudes are $o(1)$![]() and functions of $r$
and functions of $r$![]() ; $N$
; $N$![]() is the number of field periods. This form of $B$
is the number of field periods. This form of $B$![]() models Wendelstein-type configurations, where harmonics neglected in (2.1) are an order of magnitude smaller than $\epsilon _{{\rm h,m,t},0}$
models Wendelstein-type configurations, where harmonics neglected in (2.1) are an order of magnitude smaller than $\epsilon _{{\rm h,m,t},0}$![]() , with the addition of the ’anti-helical’ harmonic. To simplify calculations, we neglect the radial electric field $E_{\rm r}$
, with the addition of the ’anti-helical’ harmonic. To simplify calculations, we neglect the radial electric field $E_{\rm r}$![]() , as $E_{\rm r}$
, as $E_{\rm r}$![]() predicted by neoclassical calculation in a Helias reactor (Warmer et al. Reference Warmer, Beidler, Dinklage and Wolf2016) are too small to affect the motion of $3.5$
predicted by neoclassical calculation in a Helias reactor (Warmer et al. Reference Warmer, Beidler, Dinklage and Wolf2016) are too small to affect the motion of $3.5$![]() MeV fusion alpha particles; the influence of $E_{\rm r}$
MeV fusion alpha particles; the influence of $E_{\rm r}$![]() becomes important only after these particles slow down and lose most of their energy (Tykhyy & Kolesnichenko Reference Tykhyy and Kolesnichenko2021).
becomes important only after these particles slow down and lose most of their energy (Tykhyy & Kolesnichenko Reference Tykhyy and Kolesnichenko2021).
The $(1, -1)$![]() anti-helical harmonic has the same period in $\varphi$
anti-helical harmonic has the same period in $\varphi$![]() as do the mirror and helical harmonics. This circumstance enables us to use the approach of Beidler et al. (Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001) and combine it with the latter two harmonics:
as do the mirror and helical harmonics. This circumstance enables us to use the approach of Beidler et al. (Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001) and combine it with the latter two harmonics:
where
and $\chi (r,\vartheta )$![]() is a function indicating the position of local magnetic wells in the toroidal direction, for which we do not need an explicit expression. Expression (2.3) for $\epsilon _{\rm hm}$
is a function indicating the position of local magnetic wells in the toroidal direction, for which we do not need an explicit expression. Expression (2.3) for $\epsilon _{\rm hm}$![]() reduces to the previously known one when $\epsilon _{\rm H}=0$
reduces to the previously known one when $\epsilon _{\rm H}=0$![]() .
.
In the absence of an electric field, the parallel velocity of particles is given by $mv_\|^2/2=\mathcal {E}-\mu B=\mu \bar {B}(\alpha -B/\bar {B})$![]() , where $m$
, where $m$![]() , $\mathcal {E}$
, $\mathcal {E}$![]() and $\mu$
and $\mu$![]() are the particle mass, energy and magnetic moment, respectively, and $\alpha =\mathcal {E}/\mu \bar {B}-1$
are the particle mass, energy and magnetic moment, respectively, and $\alpha =\mathcal {E}/\mu \bar {B}-1$![]() is a pitch angle parameter. Here $\mathcal {E}$
is a pitch angle parameter. Here $\mathcal {E}$![]() , $\mu$
, $\mu$![]() and $\alpha$
and $\alpha$![]() are constants of motion. In an imperfectly symmetric magnetic field, there are three groups of particles: passing particles, which never reflect from maxima of $B$
are constants of motion. In an imperfectly symmetric magnetic field, there are three groups of particles: passing particles, which never reflect from maxima of $B$![]() (their $v_\|$
(their $v_\|$![]() is never zero); localised particles, which are always trapped in a local magnetic well; and transitioning particles, which can change between locally trapped and locally passing states, i.e. trap into and de-trap from local magnetic wells, during their drift motion. When $B$
is never zero); localised particles, which are always trapped in a local magnetic well; and transitioning particles, which can change between locally trapped and locally passing states, i.e. trap into and de-trap from local magnetic wells, during their drift motion. When $B$![]() is given by (2.1), the parallel velocity is given by $mv_\|^2/2=2\mu \bar {B}\epsilon _{\rm hm}(\kappa ^2-\sin ^2N(\varphi -\chi )/2)$
is given by (2.1), the parallel velocity is given by $mv_\|^2/2=2\mu \bar {B}\epsilon _{\rm hm}(\kappa ^2-\sin ^2N(\varphi -\chi )/2)$![]() , where
, where
is a trapping parameter which characterises the motion of particles in local magnetic wells. Particles with $\kappa ^2<1$![]() are locally trapped, and particles with $\kappa ^2>1$
are locally trapped, and particles with $\kappa ^2>1$![]() are locally passing. The equation of the separatrix between locally trapped and locally passing motion is $\kappa ^2=1$
are locally passing. The equation of the separatrix between locally trapped and locally passing motion is $\kappa ^2=1$![]() , which yields
, which yields
A particle with a given pitch-angle parameter $\alpha$![]() and starting location is transitioning when $\kappa ^2=1$
and starting location is transitioning when $\kappa ^2=1$![]() at some point in its drift orbit, i.e. if the contour of the longitudinal adiabatic invariant $J_\|$
at some point in its drift orbit, i.e. if the contour of the longitudinal adiabatic invariant $J_\|$![]() of particle drift motion which passes through the particle starting location intersects the separatrix:
of particle drift motion which passes through the particle starting location intersects the separatrix:
The derivation of expressions for $J_\|$![]() is identical to that in the case without anti-helical harmonic, because it is absorbed into $\epsilon _\textrm {hm}$
is identical to that in the case without anti-helical harmonic, because it is absorbed into $\epsilon _\textrm {hm}$![]() . We accordingly only give the results for locally trapped ($J_{\|\textrm {t}}$
. We accordingly only give the results for locally trapped ($J_{\|\textrm {t}}$![]() ) and locally passing ($J_{\|\textrm {p}}$
) and locally passing ($J_{\|\textrm {p}}$![]() ) particles (Beidler et al. Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001; Tykhyy Reference Tykhyy2018):
) particles (Beidler et al. Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001; Tykhyy Reference Tykhyy2018):
where $\boldsymbol {K}$![]() and $\boldsymbol {E}$
and $\boldsymbol {E}$![]() are the complete elliptic integrals of the first and second kind, respectively, $I_\textrm {s}=(4/{\rm \pi} N)m\omega _\textrm {B}\bar {\rho }_\textrm {L} R$
are the complete elliptic integrals of the first and second kind, respectively, $I_\textrm {s}=(4/{\rm \pi} N)m\omega _\textrm {B}\bar {\rho }_\textrm {L} R$![]() , $e$
, $e$![]() is the particle charge, $\psi _\textrm {p}$
is the particle charge, $\psi _\textrm {p}$![]() is the poloidal magnetic flux, $\omega _\textrm {B}$
is the poloidal magnetic flux, $\omega _\textrm {B}$![]() is the gyrofrequency, $\bar {\rho }_\textrm {L}$
is the gyrofrequency, $\bar {\rho }_\textrm {L}$![]() is the particle Larmor radius on the magnetic axis and $R$
is the particle Larmor radius on the magnetic axis and $R$![]() is the major radius of the torus.
is the major radius of the torus.
The adiabatic invariant $J_\|$![]() is not conserved when a particle drift orbit crosses the separatrix. This may lead to stochastic diffusion as random jumps in $J_\|$
is not conserved when a particle drift orbit crosses the separatrix. This may lead to stochastic diffusion as random jumps in $J_\|$![]() accumulate (Beidler et al. Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001; Tykhyy Reference Tykhyy2018). The eventual fate of a particle affected by stochastic diffusion depends on the shape of the separatrix, because while $\alpha$
accumulate (Beidler et al. Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001; Tykhyy Reference Tykhyy2018). The eventual fate of a particle affected by stochastic diffusion depends on the shape of the separatrix, because while $\alpha$![]() is considered constant (i.e. on time scales shorter than pitch-angle scattering time) a particle's drift orbit intersects the same separatrix while its $J_\|$
is considered constant (i.e. on time scales shorter than pitch-angle scattering time) a particle's drift orbit intersects the same separatrix while its $J_\|$![]() changes. If the separatrix of a given particle is closed within the plasma volume, the particle will be confined despite undergoing stochastic diffusion, and vice versa (Tykhyy et al. Reference Tykhyy, Kolesnichenko, Yakovenko, Weller and Werner2007) (provided that drift orbits are closer to $r=\mathrm {const.}$
changes. If the separatrix of a given particle is closed within the plasma volume, the particle will be confined despite undergoing stochastic diffusion, and vice versa (Tykhyy et al. Reference Tykhyy, Kolesnichenko, Yakovenko, Weller and Werner2007) (provided that drift orbits are closer to $r=\mathrm {const.}$![]() than the separatrix, as is the case in Wendelstein-type configurations; however, it is desirable for drift orbits to be close to $r=\mathrm {const.}$
than the separatrix, as is the case in Wendelstein-type configurations; however, it is desirable for drift orbits to be close to $r=\mathrm {const.}$![]() from many considerations and this property is one of stellarator optimisation criteria). Note that minor harmonics of $B$
from many considerations and this property is one of stellarator optimisation criteria). Note that minor harmonics of $B$![]() omitted from (2.1) may cause particles which are confined in the model magnetic field to be lost from the plasma. However, the time scale for such losses will be longer as the coefficient of stochastic diffusion scales with magnetic field harmonics (Tykhyy Reference Tykhyy2018; Tykhyy & Kolesnichenko Reference Tykhyy and Kolesnichenko2021). If this longer time scale exceeds particle slowing-down time, collisionless stochastic losses via minor harmonics become unimportant. This means that sufficiently small minor harmonics of $B$
omitted from (2.1) may cause particles which are confined in the model magnetic field to be lost from the plasma. However, the time scale for such losses will be longer as the coefficient of stochastic diffusion scales with magnetic field harmonics (Tykhyy Reference Tykhyy2018; Tykhyy & Kolesnichenko Reference Tykhyy and Kolesnichenko2021). If this longer time scale exceeds particle slowing-down time, collisionless stochastic losses via minor harmonics become unimportant. This means that sufficiently small minor harmonics of $B$![]() may be safely neglected for the purpose of collisionless stochastic losses.
may be safely neglected for the purpose of collisionless stochastic losses.
Particle drift orbits are the contours of $J_\|$![]() . Expressions (2.7a,b) for $J_\|$
. Expressions (2.7a,b) for $J_\|$![]() involve elliptic integrals, and thus one needs to solve (2.6) numerically to follow drift orbits and determine whether a given particle is transitioning, localised or passing. The results of these calculations are presented in the next section. The radial deviation of drift orbits from magnetic surfaces (i.e. orbit width) also needs to be computed numerically. However, for passing particles, the $\vartheta$
involve elliptic integrals, and thus one needs to solve (2.6) numerically to follow drift orbits and determine whether a given particle is transitioning, localised or passing. The results of these calculations are presented in the next section. The radial deviation of drift orbits from magnetic surfaces (i.e. orbit width) also needs to be computed numerically. However, for passing particles, the $\vartheta$![]() -independent term in $\psi _\textrm {p}$
-independent term in $\psi _\textrm {p}$![]() is of the same order (for $3.5$
is of the same order (for $3.5$![]() MeV alphas in a Helias reactor) or larger than the term with $I_\textrm {s}$
MeV alphas in a Helias reactor) or larger than the term with $I_\textrm {s}$![]() , which means that passing particle drift orbits are narrow. For locally trapped particles, this is not the case.
, which means that passing particle drift orbits are narrow. For locally trapped particles, this is not the case.
We proceed to examine analytically the shape of the separatrix, following the procedure in Appendix A of Kolesnichenko et al. (Reference Kolesnichenko, Lutsenko and Tykhyy2022). The maximum and minimum values of $r$![]() on a separatrix are determined by the equation
on a separatrix are determined by the equation

we omit the cumbersome denominator containing the derivatives in $r$![]() . When $\epsilon _\textrm {H}=0$
. When $\epsilon _\textrm {H}=0$![]() and the other harmonics are positive, the numerator of the fraction in the right-hand side of (2.8) is never zero and (2.8) has roots only on the midplane of the torus $\vartheta =\{0,{\rm \pi} \}$
and the other harmonics are positive, the numerator of the fraction in the right-hand side of (2.8) is never zero and (2.8) has roots only on the midplane of the torus $\vartheta =\{0,{\rm \pi} \}$![]() . In a bi-helical configuration with $\epsilon _\textrm {H}>0$
. In a bi-helical configuration with $\epsilon _\textrm {H}>0$![]() this is no longer necessarily true, e.g. in a high-mirror Wendelstein configuration with enhanced $(1, -1)$
this is no longer necessarily true, e.g. in a high-mirror Wendelstein configuration with enhanced $(1, -1)$![]() harmonic additional off-midplane roots appear at $r/a=0.5$
harmonic additional off-midplane roots appear at $r/a=0.5$![]() when $\epsilon _\textrm {H}>0.055(r/a)$
when $\epsilon _\textrm {H}>0.055(r/a)$![]() , indicating that the separatrix becomes somewhat rounded. However, the midplane roots are still indicative of the location and extent of the separatrix. Accordingly we consider only those roots of (2.8) which lie on the midplane.
, indicating that the separatrix becomes somewhat rounded. However, the midplane roots are still indicative of the location and extent of the separatrix. Accordingly we consider only those roots of (2.8) which lie on the midplane.
Let us first approximate the harmonics of the magnetic field with linear (for helical and toroidal harmonics) and quadratic (for mirror and diamagnetic harmonics) functions of $x\equiv r/a$![]() :
:
where $\bar \epsilon _\textrm {m}=\mathrm {const.}$![]() and coefficients $k_i=\mathrm {const}$
and coefficients $k_i=\mathrm {const}$![]() . This approximation is rather good in the plasma core of Wendelstein-type configurations: with suitable values of $k_i$
. This approximation is rather good in the plasma core of Wendelstein-type configurations: with suitable values of $k_i$![]() , deviations of harmonics from (2.9a–e) do not exceed $5\,\%$
, deviations of harmonics from (2.9a–e) do not exceed $5\,\%$![]() when $r/a<0.5$
when $r/a<0.5$![]() , which is of the same order as the minor harmonics not included in the model magnetic field (2.1), and its simplicity allows us to obtain analytical expressions characterising the separatrix.
, which is of the same order as the minor harmonics not included in the model magnetic field (2.1), and its simplicity allows us to obtain analytical expressions characterising the separatrix.
With the harmonics given by (2.9a–e), (2.5) at $\vartheta =\{0,{\rm \pi} \}$![]() reduces to a quadratic equation in $x$
reduces to a quadratic equation in $x$![]() with the roots (Kolesnichenko et al. Reference Kolesnichenko, Lutsenko and Tykhyy2022)
with the roots (Kolesnichenko et al. Reference Kolesnichenko, Lutsenko and Tykhyy2022)
where
The separatrix exists when $\mathcal {D}>0$![]() , i.e. when $\alpha >\alpha ^\textrm {t}_\textrm {min}\equiv \bar \epsilon _\textrm {m}-(k_0+k_\textrm {m})\bar {k}^2$
, i.e. when $\alpha >\alpha ^\textrm {t}_\textrm {min}\equiv \bar \epsilon _\textrm {m}-(k_0+k_\textrm {m})\bar {k}^2$![]() . Here $\alpha ^\textrm {t}_\textrm {min}$
. Here $\alpha ^\textrm {t}_\textrm {min}$![]() is the lower bound of the range of pitch angles in which transitioning particles can exist; particles with $\alpha <\alpha ^\textrm {t}_\textrm {min}$
is the lower bound of the range of pitch angles in which transitioning particles can exist; particles with $\alpha <\alpha ^\textrm {t}_\textrm {min}$![]() are localised.
are localised.
When $\mathcal {D}>0$![]() , (2.8) has two positive roots; negative roots must be discarded because $x=r/a$
, (2.8) has two positive roots; negative roots must be discarded because $x=r/a$![]() is a radial coordinate. We consider only the case of $\bar {k}>0$
is a radial coordinate. We consider only the case of $\bar {k}>0$![]() , which holds even for bi-helical configurations in which the strengths of the $(1, -1)$
, which holds even for bi-helical configurations in which the strengths of the $(1, -1)$![]() and $(1,1)$
and $(1,1)$![]() helical harmonics are equal. In this case, when $\sqrt{\mathcal{D}} < \bar {k}$
helical harmonics are equal. In this case, when $\sqrt{\mathcal{D}} < \bar {k}$![]() the two positive roots are provided by (2.10); this means that the separatrix does not encircle the magnetic axis and is located towards the outer circumference of the torus. When $\sqrt{\mathcal D}>\bar {k}$
the two positive roots are provided by (2.10); this means that the separatrix does not encircle the magnetic axis and is located towards the outer circumference of the torus. When $\sqrt{\mathcal D}>\bar {k}$![]() , the two positive roots are those with the upper signs of (2.10) and (2.11). The maximum radius of the separatrix is $x_\textrm {max}=\bar {k}+\sqrt {\mathcal D}$
, the two positive roots are those with the upper signs of (2.10) and (2.11). The maximum radius of the separatrix is $x_\textrm {max}=\bar {k}+\sqrt {\mathcal D}$![]() in both cases. The separatrix is closed within the plasma when $x_\textrm {max}<1$
in both cases. The separatrix is closed within the plasma when $x_\textrm {max}<1$![]() . It is obvious that $x_\textrm {max}$
. It is obvious that $x_\textrm {max}$![]() becomes smaller as $k_\textrm {H}$
becomes smaller as $k_\textrm {H}$![]() increases and $\bar {k}$
increases and $\bar {k}$![]() decreases: i.e. the gap between the outer edge of the separatrix and the plasma boundary is larger in a bi-helical configuration than in a regular one.
decreases: i.e. the gap between the outer edge of the separatrix and the plasma boundary is larger in a bi-helical configuration than in a regular one.
The equation $x_\textrm {max}=1$![]() provides the upper limit of the range of pitch angles for which transitioning particles are never lost from the plasma due to stochastic diffusion. It yields $\alpha _\textrm {max}=\bar \epsilon _\textrm {m}+(k_0+k_\textrm {m})(1-2\bar {k})= \bar \epsilon _\textrm {m}+k_\textrm {m}+k_0-k_\textrm {t}-k_\textrm {h}+k_\textrm {H}$
provides the upper limit of the range of pitch angles for which transitioning particles are never lost from the plasma due to stochastic diffusion. It yields $\alpha _\textrm {max}=\bar \epsilon _\textrm {m}+(k_0+k_\textrm {m})(1-2\bar {k})= \bar \epsilon _\textrm {m}+k_\textrm {m}+k_0-k_\textrm {t}-k_\textrm {h}+k_\textrm {H}$![]() . This upper limit also increases very considerably when $k_\textrm {H}$
. This upper limit also increases very considerably when $k_\textrm {H}$![]() increases; in an otherwise typical high-mirror Helias configuration setting $k_\textrm {H}=k_\textrm {h}$
increases; in an otherwise typical high-mirror Helias configuration setting $k_\textrm {H}=k_\textrm {h}$![]() changes $\alpha _\textrm {max}$
changes $\alpha _\textrm {max}$![]() from $0.147$
from $0.147$![]() to $0.225$
to $0.225$![]() , more than doubling the range of confined pitch angles. It is also clear that $x_\textrm {max}$
, more than doubling the range of confined pitch angles. It is also clear that $x_\textrm {max}$![]() decreases and $\alpha _\textrm {max}$
decreases and $\alpha _\textrm {max}$![]() increases with increasing $k_\textrm {m}$
increases with increasing $k_\textrm {m}$![]() and $k_0$
and $k_0$![]() (i.e. plasma diamagnetism). This leads one to expect worse confinement of energetic ions on the plasma periphery in a realistic magnetic configuration in which mirror and diamagnetic harmonics are linear outside of plasma core.
(i.e. plasma diamagnetism). This leads one to expect worse confinement of energetic ions on the plasma periphery in a realistic magnetic configuration in which mirror and diamagnetic harmonics are linear outside of plasma core.
Parameters such as $x_\textrm {max}$![]() , $\alpha ^\textrm {t}_\textrm {min}$
, $\alpha ^\textrm {t}_\textrm {min}$![]() and $\alpha _\textrm {max}$
and $\alpha _\textrm {max}$![]() are useful because they describe generalised features of transitioning particle confinement and have simple analytical expressions in model configurations that can be described by (2.9a–e). However, they do not provide a full picture of the behaviour of drift orbits (contour lines of $J_\|$
are useful because they describe generalised features of transitioning particle confinement and have simple analytical expressions in model configurations that can be described by (2.9a–e). However, they do not provide a full picture of the behaviour of drift orbits (contour lines of $J_\|$![]() ). As mentioned previously, the expressions for $J_\|$
). As mentioned previously, the expressions for $J_\|$![]() involve elliptic integrals, which makes it impossible to obtain analytical estimates for e.g. the width of the drift orbits of trapped particles (for passing fast particles the term in $\psi$
involve elliptic integrals, which makes it impossible to obtain analytical estimates for e.g. the width of the drift orbits of trapped particles (for passing fast particles the term in $\psi$![]() in (2.7a,b) ensures that orbit width is small). In addition, more realistic magnetic configurations with reduced plasma diamagnetism towards the periphery cannot be described by (2.9a–e). Therefore, in the next section we study particle drift orbits by integrating (2.7a,b) numerically.
in (2.7a,b) ensures that orbit width is small). In addition, more realistic magnetic configurations with reduced plasma diamagnetism towards the periphery cannot be described by (2.9a–e). Therefore, in the next section we study particle drift orbits by integrating (2.7a,b) numerically.
3. Numerical investigation of marginal drift orbits
As remarked in the preceding section, the approximation of magnetic field harmonics in (2.9a–e) in which mirror and diamagnetic harmonics are purely quadratic in $r/a$![]() is suitable for deriving simple analytical expressions describing the separatrix, but applies only in the plasma core of realistic Wendelstein-type configurations. In the latter, outside the radius $r/a\approx 0.6$
is suitable for deriving simple analytical expressions describing the separatrix, but applies only in the plasma core of realistic Wendelstein-type configurations. In the latter, outside the radius $r/a\approx 0.6$![]() mirror and diamagnetic harmonics are close to linear in $r/a$
mirror and diamagnetic harmonics are close to linear in $r/a$![]() as bulk plasma pressure falls off and plasma diamagnetism decreases. This difference is important because the poloidal drift, which makes particle orbits close to flux surfaces, depends on the second derivatives of these harmonics. This means that the analytical estimates of separatrix shape made in the preceding section are optimistic.
as bulk plasma pressure falls off and plasma diamagnetism decreases. This difference is important because the poloidal drift, which makes particle orbits close to flux surfaces, depends on the second derivatives of these harmonics. This means that the analytical estimates of separatrix shape made in the preceding section are optimistic.
Accordingly, for the numerical calculations of this section, we approximate $\epsilon _\textrm {m}$![]() and $\epsilon _0$
and $\epsilon _0$![]() with piecewise quadratic and linear functions having a smooth first derivative:
with piecewise quadratic and linear functions having a smooth first derivative:
with $x_*=0.6$![]() . This approximation is good for all $r$
. This approximation is good for all $r$![]() : the deviations are on the order of the minor harmonics of the magnetic field neglected in (2.1).
: the deviations are on the order of the minor harmonics of the magnetic field neglected in (2.1).
In the following, we investigate the effect of adding an anti-helical harmonic to an example magnetic configuration on fast particle drift orbits. We employ a numerical code developed for this paper which solves (2.6) to find marginal drift orbits: the drift orbits which divide the poloidal cross-section of the plasma into areas where drift orbits behave in a similar fashion. The marginal drift orbits which the code can locate are $\mathcal {O}_\textrm {p}$![]() , the passing particle orbit which just touches the separatrix from the inside (all passing particle orbits for a given $\alpha$
, the passing particle orbit which just touches the separatrix from the inside (all passing particle orbits for a given $\alpha$![]() are nested within this orbit), $\mathcal {O}_\textrm {t}$
are nested within this orbit), $\mathcal {O}_\textrm {t}$![]() , the localised particle orbit which just touches the separatrix from the outside (all transitioning particle orbits for a given $\alpha$
, the localised particle orbit which just touches the separatrix from the outside (all transitioning particle orbits for a given $\alpha$![]() are nested within this orbit), and $\mathcal {O}_\textrm {l}$
are nested within this orbit), and $\mathcal {O}_\textrm {l}$![]() , the localised particle orbit which just touches the edge of the plasma, if it exists (all confined orbits of localised particles are nested within this orbit). The code also integrates drift equations obtained from (2.7a,b) to trace orbits with a given $\alpha$
, the localised particle orbit which just touches the edge of the plasma, if it exists (all confined orbits of localised particles are nested within this orbit). The code also integrates drift equations obtained from (2.7a,b) to trace orbits with a given $\alpha$![]() passing through a given point. Plotted together with the separatrix, marginal orbits help visualise the areas of poloidal cross-section occupied by the various kinds of particles and to distinguish cases when particles are confined or lost. $\mathcal {O}_\textrm {t}$
passing through a given point. Plotted together with the separatrix, marginal orbits help visualise the areas of poloidal cross-section occupied by the various kinds of particles and to distinguish cases when particles are confined or lost. $\mathcal {O}_\textrm {t}$![]() contains transitioning particle orbits affected by stochastic diffusion; these particles are lost from the plasma when $\mathcal {O}_\textrm {t}$
contains transitioning particle orbits affected by stochastic diffusion; these particles are lost from the plasma when $\mathcal {O}_\textrm {t}$![]() intersects the plasma boundary, but are confined when $\mathcal {O}_\textrm {t}$
intersects the plasma boundary, but are confined when $\mathcal {O}_\textrm {t}$![]() lies entirely within the plasma volume. The gap between $\mathcal {O}_\textrm {l}$
lies entirely within the plasma volume. The gap between $\mathcal {O}_\textrm {l}$![]() and $\mathcal {O}_\textrm {t}$
and $\mathcal {O}_\textrm {t}$![]() indicates the fraction of localised particles which are confined within the plasma and not subject to stochastic diffusion, and $\mathcal {O}_\textrm {p}$
indicates the fraction of localised particles which are confined within the plasma and not subject to stochastic diffusion, and $\mathcal {O}_\textrm {p}$![]() contains passing orbits, which are almost always confined as their orbit width is small.
contains passing orbits, which are almost always confined as their orbit width is small.
Figure 1 shows how the behaviour of marginal drift orbits in the same model high-mirror Helias magnetic configuration with $\langle \beta \rangle =4.7\,\%$![]() which was used in numerical part of Beidler et al. (Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001), with mirror and diamagnetic harmonics linear outside $r/a=0.6$
which was used in numerical part of Beidler et al. (Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001), with mirror and diamagnetic harmonics linear outside $r/a=0.6$![]() as described by (3.1a,b), changes with enhanced anti-helical harmonic. In this configuration with $k_\textrm {H}=0$
as described by (3.1a,b), changes with enhanced anti-helical harmonic. In this configuration with $k_\textrm {H}=0$![]() , transitioning particles exist for $\alpha >\alpha _\textrm {min}\approx 0.09$
, transitioning particles exist for $\alpha >\alpha _\textrm {min}\approx 0.09$![]() . The range of $\alpha$
. The range of $\alpha$![]() for which transitioning particles are confined is very small, $0.09<\alpha <0.114$
for which transitioning particles are confined is very small, $0.09<\alpha <0.114$![]() . Transitioning particles with $\alpha >0.114$
. Transitioning particles with $\alpha >0.114$![]() are lost due to stochastic diffusion, and almost all localised particles outside this region are lost on the drift time scale. Only passing energetic particles are confined completely. Note that for trapped fusion alphas with $\alpha \lesssim 0.3$
are lost due to stochastic diffusion, and almost all localised particles outside this region are lost on the drift time scale. Only passing energetic particles are confined completely. Note that for trapped fusion alphas with $\alpha \lesssim 0.3$![]() , fraction of alphas born with $\alpha _1<\alpha <\alpha _2$
, fraction of alphas born with $\alpha _1<\alpha <\alpha _2$![]() is approximately $\sim |\alpha _2-\alpha _1|$
is approximately $\sim |\alpha _2-\alpha _1|$![]() .
.

Figure 1. Dependence of drift orbit confinement on the ratio of anti-helical to helical harmonics $\nu _\textrm {h}\equiv |\epsilon _{1,-1}/\epsilon _{1,1}|=k_\textrm {H}/k_\textrm {h}$![]() in a high-mirror Helias configuration with $\langle \beta \rangle =4.7\,\%$
in a high-mirror Helias configuration with $\langle \beta \rangle =4.7\,\%$![]() . Plots of marginal drift orbits in the poloidal cross-section of the torus in magnetic coordinates $(X=r/a\cos \vartheta,Y=r/a\sin \vartheta )$
. Plots of marginal drift orbits in the poloidal cross-section of the torus in magnetic coordinates $(X=r/a\cos \vartheta,Y=r/a\sin \vartheta )$![]() . Columns show increasing pitch-angle parameter $\alpha$
. Columns show increasing pitch-angle parameter $\alpha$![]() and rows show increasing $\nu _\textrm {h}$
and rows show increasing $\nu _\textrm {h}$![]() . For each $k_\textrm {H}$
. For each $k_\textrm {H}$![]() , $\alpha$
, $\alpha$![]() values slightly less than $\alpha _\textrm {max}(k_\textrm {H})$
values slightly less than $\alpha _\textrm {max}(k_\textrm {H})$![]() (maximum $\alpha$
(maximum $\alpha$![]() for which the separatrix closes inside the plasma) are shown. Thick black line: separatrix $\kappa ^2=1$
for which the separatrix closes inside the plasma) are shown. Thick black line: separatrix $\kappa ^2=1$![]() . Thin lines separating hatched areas: marginal drift orbits. Hatching identifies regions of poloidal cross-section where particles with given $\alpha$
. Thin lines separating hatched areas: marginal drift orbits. Hatching identifies regions of poloidal cross-section where particles with given $\alpha$![]() have orbits of one type. No hatching: passing orbits, never lost. Dots: localised orbits, never lost. Vertical lines: transitioning orbits affected by stochastic diffusion but never lost. Diagonal lines: transitioning orbits lost on diffusion time scale. Horizontal lines: localised orbits, lost on drift timescale. For trapped fusion alphas with $\alpha \lesssim 0.3$
have orbits of one type. No hatching: passing orbits, never lost. Dots: localised orbits, never lost. Vertical lines: transitioning orbits affected by stochastic diffusion but never lost. Diagonal lines: transitioning orbits lost on diffusion time scale. Horizontal lines: localised orbits, lost on drift timescale. For trapped fusion alphas with $\alpha \lesssim 0.3$![]() , the fraction of alphas born with $\alpha _1<\alpha <\alpha _2$
, the fraction of alphas born with $\alpha _1<\alpha <\alpha _2$![]() is approximately $\sim |\alpha _2-\alpha _1|$
is approximately $\sim |\alpha _2-\alpha _1|$![]() .
.
The addition of even a relatively small anti-helical harmonic $\nu _\textrm {h}\equiv k_\textrm {H}/k_\textrm {h}=25\,\%$![]() markedly improves the picture. $\alpha _\textrm {max}$
markedly improves the picture. $\alpha _\textrm {max}$![]() increases to $0.135$
increases to $0.135$![]() , meaning that more transitioning particles are confined, and a gap opens between $\mathcal {O}_\textrm {l}$
, meaning that more transitioning particles are confined, and a gap opens between $\mathcal {O}_\textrm {l}$![]() and $\mathcal {O}_\textrm {t}$
and $\mathcal {O}_\textrm {t}$![]() , indicating that many localised particles are now confined along with passing particles. The area of confined passing particles $\mathcal {O}_\textrm {p}$
, indicating that many localised particles are now confined along with passing particles. The area of confined passing particles $\mathcal {O}_\textrm {p}$![]() at this $\alpha$
at this $\alpha$![]() barely extends past $r/a=0.1$
barely extends past $r/a=0.1$![]() , indicating that stochastic diffusion losses from the plasma core are still large. Confinement improves still further as $k_\textrm {H}$
, indicating that stochastic diffusion losses from the plasma core are still large. Confinement improves still further as $k_\textrm {H}$![]() approaches $k_\textrm {h}$
approaches $k_\textrm {h}$![]() . With $\nu _\textrm {h}=85\,\%$
. With $\nu _\textrm {h}=85\,\%$![]() , $\alpha _\textrm {max}$
, $\alpha _\textrm {max}$![]() increases to $0.185$
increases to $0.185$![]() , and at this $\alpha$
, and at this $\alpha$![]() , $\mathcal {O}_\textrm {p}$
, $\mathcal {O}_\textrm {p}$![]() covers the whole core plasma area $r/a<0.5$
covers the whole core plasma area $r/a<0.5$![]() . This means that both drift and stochastic diffusion losses of energetic particles from the core plasma area are almost completely mitigated. Increasing $\nu _\textrm {h}$
. This means that both drift and stochastic diffusion losses of energetic particles from the core plasma area are almost completely mitigated. Increasing $\nu _\textrm {h}$![]() still further brings little benefit in terms of $\alpha _\textrm {max}$
still further brings little benefit in terms of $\alpha _\textrm {max}$![]() : it increases only from $0.185$
: it increases only from $0.185$![]() for $\nu _\textrm {h}=85\,\%$
for $\nu _\textrm {h}=85\,\%$![]() to $0.198$
to $0.198$![]() for $\nu _\textrm {h}=1$
for $\nu _\textrm {h}=1$![]() . Figure 1 uses $\alpha$
. Figure 1 uses $\alpha$![]() values close to the $\alpha _\textrm {max}$
values close to the $\alpha _\textrm {max}$![]() values for three values of $\nu _\textrm {h}$
values for three values of $\nu _\textrm {h}$![]() ($0$
($0$![]() , $25\,\%$
, $25\,\%$![]() and $85\,\%$
and $85\,\%$![]() ).
).
Figure 2 shows how much difference the decline of plasma diamagnetism towards the edge makes for energetic ion drift orbit confinement. For illustration, the value of $\alpha =0.13$![]() is chosen which is close to $\alpha _\textrm {max}$
is chosen which is close to $\alpha _\textrm {max}$![]() for the configuration given by (2.9a–e) with $k_\textrm {H}=0$
for the configuration given by (2.9a–e) with $k_\textrm {H}=0$![]() and purely quadratic radial dependence of mirror and diamagnetic harmonics, so that the separatrix is closed within the plasma volume with a small gap (left diagram in figure 2). This means that transitioning particles and a fraction of locally trapped particles are confined. The right diagram in figure 2 shows marginal drift orbits in the configuration given by (3.1a,b), which is the same except for mirror and diamagnetic harmonics being linear in $r$
and purely quadratic radial dependence of mirror and diamagnetic harmonics, so that the separatrix is closed within the plasma volume with a small gap (left diagram in figure 2). This means that transitioning particles and a fraction of locally trapped particles are confined. The right diagram in figure 2 shows marginal drift orbits in the configuration given by (3.1a,b), which is the same except for mirror and diamagnetic harmonics being linear in $r$![]() beyond $r/a=0.6$
beyond $r/a=0.6$![]() . As the analysis of the preceding section predicts, the gap between plasma boundary and transitioning particle area disappears, the separatrix intersects the plasma boundary, and transitioning particles are no longer confined but are lost on stochastic diffusion time scale. In addition, all locally trapped particles are lost on the drift time scale. The effect is qualitatively the same for all pitch angles. Numerical calculations show that in the configuration given by (2.9a–e) the range of pitch angles in which transitioning particles are confined is ${\rm \Delta} \alpha \approx 0.047$
. As the analysis of the preceding section predicts, the gap between plasma boundary and transitioning particle area disappears, the separatrix intersects the plasma boundary, and transitioning particles are no longer confined but are lost on stochastic diffusion time scale. In addition, all locally trapped particles are lost on the drift time scale. The effect is qualitatively the same for all pitch angles. Numerical calculations show that in the configuration given by (2.9a–e) the range of pitch angles in which transitioning particles are confined is ${\rm \Delta} \alpha \approx 0.047$![]() , whereas in the more realistic configuration given by (3.1a,b) ${\rm \Delta} \alpha$
, whereas in the more realistic configuration given by (3.1a,b) ${\rm \Delta} \alpha$![]() is only $0.022$
is only $0.022$![]() , indicating worse trapped and transitioning particle confinement due to reduced diamagnetic drift outside the plasma core. Enhancing the anti-helical harmonic to $25\,\%$
, indicating worse trapped and transitioning particle confinement due to reduced diamagnetic drift outside the plasma core. Enhancing the anti-helical harmonic to $25\,\%$![]() of the helical harmonic in the former configuration only slightly increases ${\rm \Delta} \alpha$
of the helical harmonic in the former configuration only slightly increases ${\rm \Delta} \alpha$![]() to $0.055$
to $0.055$![]() (by less than a fifth). In contrast, enhancing the anti-helical harmonic by the same amount in the latter configuration increases ${\rm \Delta} \alpha$
(by less than a fifth). In contrast, enhancing the anti-helical harmonic by the same amount in the latter configuration increases ${\rm \Delta} \alpha$![]() from $0.022$
from $0.022$![]() to $0.035$
to $0.035$![]() (by $60\,\%$
(by $60\,\%$![]() ). Enhancing the anti-helical harmonic by a larger amount, to $\nu _\textrm {h}=85\,\%$
). Enhancing the anti-helical harmonic by a larger amount, to $\nu _\textrm {h}=85\,\%$![]() , doubles ${\rm \Delta} \alpha$
, doubles ${\rm \Delta} \alpha$![]() in the former configuration, but more than triples it in the latter. That is, enhancing the anti-helical harmonic by the same amount brings more benefit for the confinement of trapped and transitioning particles in the more realistic configuration where diamagnetic drift outside the plasma core is weak.
in the former configuration, but more than triples it in the latter. That is, enhancing the anti-helical harmonic by the same amount brings more benefit for the confinement of trapped and transitioning particles in the more realistic configuration where diamagnetic drift outside the plasma core is weak.

Figure 2. Effect of reduced plasma diamagnetism on the periphery on marginal drift orbits in a high-mirror Helias configuration with $\langle \beta \rangle =4.7\,\%$![]() . The pitch-angle parameter is $\alpha =0.13$
. The pitch-angle parameter is $\alpha =0.13$![]() . Anti-helical harmonic is absent. Left: mirror ($\epsilon _\textrm {m}$
. Anti-helical harmonic is absent. Left: mirror ($\epsilon _\textrm {m}$![]() ) and diamagnetic ($\epsilon _0$
) and diamagnetic ($\epsilon _0$![]() ) harmonics of $B$
) harmonics of $B$![]() are quadratic in $r/a$
are quadratic in $r/a$![]() in the whole plasma volume. Right: $\epsilon _\textrm {m}$
in the whole plasma volume. Right: $\epsilon _\textrm {m}$![]() and $\epsilon _0$
and $\epsilon _0$![]() are quadratic for $r/a<0.6$
are quadratic for $r/a<0.6$![]() and smoothly switch to linear for $r/a>0.6$
and smoothly switch to linear for $r/a>0.6$![]() . Same conventions as in figure 1.
. Same conventions as in figure 1.
4. Summary
Stochastic motion of transitioning 3.5-MeV alpha particles in a Helias reactor was observed numerically in recent work (Kolesnichenko et al. Reference Kolesnichenko, Lutsenko and Tykhyy2022). This validated theory prediction that the collisionless stochastic diffusion of these particles represents a mechanism of considerable delayed loss of fast ions in quasi-isodynamic stellarators (Beidler et al. Reference Beidler, Kolesnichenko, Marchenko, Sidorenko and Wobig2001). The numerical calculation has also demonstrated a possibility to prevent the escape of particles to the wall by making the separatrix between the locally trapped and passing states ($\kappa ^2=1$![]() ) closed, as was proposed in Tykhyy et al. (Reference Tykhyy, Kolesnichenko, Yakovenko, Weller and Werner2007). It was concluded in Kolesnichenko et al. (Reference Kolesnichenko, Lutsenko and Tykhyy2022) that potentially the fraction of particles with closed separatrix in the population of transitioning particles can be increased and, moreover, the number of transitioning particles can be reduced. This can be done by a special optimisation of the magnetic configuration, which reduces the separatrix maximum radius, $r_\textrm {max}$
) closed, as was proposed in Tykhyy et al. (Reference Tykhyy, Kolesnichenko, Yakovenko, Weller and Werner2007). It was concluded in Kolesnichenko et al. (Reference Kolesnichenko, Lutsenko and Tykhyy2022) that potentially the fraction of particles with closed separatrix in the population of transitioning particles can be increased and, moreover, the number of transitioning particles can be reduced. This can be done by a special optimisation of the magnetic configuration, which reduces the separatrix maximum radius, $r_\textrm {max}$![]() . An equation has been derived, which indicated that $r_\textrm {max}$
. An equation has been derived, which indicated that $r_\textrm {max}$![]() decreases, in particular, when the helical component of the magnetic field (${1,1}$
decreases, in particular, when the helical component of the magnetic field (${1,1}$![]() ) decreases. This result suggests that adding an enlarged ‘anti-helical component’ (${1,-1}$
) decreases. This result suggests that adding an enlarged ‘anti-helical component’ (${1,-1}$![]() ), which was proposed by Gori et al. (Reference Gori, Lotz and Nuhrenberg1994), Helander & Nuhrenberg (Reference Helander and Nuhrenberg2009), Helander et al. (Reference Helander, Geiger and Maasberg2011) and Beidler & Maasberg (Reference Beidler and Maasberg2001) to increase omnigeneity, would be favourable also for decreasing delayed losses of fast ions. This possibility is explored in this work. The obtained results can be summarised as follows.
), which was proposed by Gori et al. (Reference Gori, Lotz and Nuhrenberg1994), Helander & Nuhrenberg (Reference Helander and Nuhrenberg2009), Helander et al. (Reference Helander, Geiger and Maasberg2011) and Beidler & Maasberg (Reference Beidler and Maasberg2001) to increase omnigeneity, would be favourable also for decreasing delayed losses of fast ions. This possibility is explored in this work. The obtained results can be summarised as follows.
Equations describing orbits and the $\kappa ^2=1$![]() separatrix in quasi-isodynamic stellarators with a Wendelstein-type magnetic configuration have been generalised to include the $(1, -1)$
separatrix in quasi-isodynamic stellarators with a Wendelstein-type magnetic configuration have been generalised to include the $(1, -1)$![]() Fourier component of the magnetic field. They were used to calculate regions of location of localised, transitioning and passing particles with various magnitudes of the pitch parameter $\alpha$
Fourier component of the magnetic field. They were used to calculate regions of location of localised, transitioning and passing particles with various magnitudes of the pitch parameter $\alpha$![]() for a high-mirror configuration in the poloidal cross-section. Calculations were carried out for several magnitudes of the anti-helical harmonic; results are shown for $\nu _\textrm {h}\equiv \epsilon _\textrm {H}/\epsilon _\textrm {h}=0$
for a high-mirror configuration in the poloidal cross-section. Calculations were carried out for several magnitudes of the anti-helical harmonic; results are shown for $\nu _\textrm {h}\equiv \epsilon _\textrm {H}/\epsilon _\textrm {h}=0$![]() , 0.25 and $0.85$
, 0.25 and $0.85$![]() . Positive effects are found already at smallest considered anti-helical harmonic: when $\nu _\textrm {h}=0.25$
. Positive effects are found already at smallest considered anti-helical harmonic: when $\nu _\textrm {h}=0.25$![]() , transitioning particles with smallest and intermediate pitch parameters ($\alpha <0.18$
, transitioning particles with smallest and intermediate pitch parameters ($\alpha <0.18$![]() ) are confined, and their fraction decreased. When $\epsilon _\textrm {H}\sim \epsilon _\textrm {h}$
) are confined, and their fraction decreased. When $\epsilon _\textrm {H}\sim \epsilon _\textrm {h}$![]() ($\nu _\textrm {h}=0.85$
($\nu _\textrm {h}=0.85$![]() ), almost all transitioning particles are confined, and their fraction is minimum; well-confined localised orbits dominate at smallest $\alpha$
), almost all transitioning particles are confined, and their fraction is minimum; well-confined localised orbits dominate at smallest $\alpha$![]() ($\alpha =0.114$
($\alpha =0.114$![]() ).
).
It is shown by numerical calculations that it is important for the investigation of transitioning particle confinement to take into account the fact that plasma diamagnetism decreases towards the edge and that, as a consequence, mirror and diamagnetic harmonics have an approximately linear, rather than parabolic, radial dependence on the periphery, because in Wendelstein-type configurations without an anti-helical harmonic, transitioning particle confinement depends on diamagnetic drift. This conclusion is also applicable to other stellarators where omnigeneity/quasi-isodynamicity is achieved with the help of plasma diamagnetism.
It is concluded that the benefit of bi-helical optimisation is more pronounced in realistic magnetic configurations: enhancing the anti-helical harmonic by a given amount increases the range of pitch angles of confined trapped and transitioning fast particles by a larger factor in a magnetic configuration in which mirror and diamagnetic harmonics of the magnetic field are parabolic in $r$![]() in the plasma core but linear on the periphery, reflecting reduced plasma diamagnetism, compared with a configuration in which these harmonics are parabolic in $r$
in the plasma core but linear on the periphery, reflecting reduced plasma diamagnetism, compared with a configuration in which these harmonics are parabolic in $r$![]() in the whole plasma volume.
in the whole plasma volume.
Acknowledgements
The authors thank Per Helander for drawing their attention to publications Helander & Nuhrenberg (Reference Helander and Nuhrenberg2009), Helander et al. (Reference Helander, Geiger and Maasberg2011) and Beidler & Maasberg (Reference Beidler and Maasberg2001), and for reading and providing valuable comments on the manuscript.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.