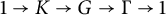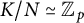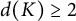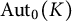1 Introduction
For a pro-p group G, we denote by
![]() $K[[G]]$
the completed group algebra of G over the ring K, where K is the field with p elements
$K[[G]]$
the completed group algebra of G over the ring K, where K is the field with p elements
![]() $\mathbb {F}_p$
or the ring of the p-adic numbers
$\mathbb {F}_p$
or the ring of the p-adic numbers
![]() $\mathbb {Z}_p$
. By definition a pro-p group G is of type
$\mathbb {Z}_p$
. By definition a pro-p group G is of type
![]() $FP_m$
if the trivial
$FP_m$
if the trivial
![]() $\mathbb {Z}_p[[G]]$
-module
$\mathbb {Z}_p[[G]]$
-module
![]() $\mathbb {Z}_p$
has a projective resolution where all projectives in dimension
$\mathbb {Z}_p$
has a projective resolution where all projectives in dimension
![]() $\leq m$
are finitely generated
$\leq m$
are finitely generated
![]() $\mathbb {Z}_p[[G]]$
-modules. Note that G is of type
$\mathbb {Z}_p[[G]]$
-modules. Note that G is of type
![]() $FP_1$
if and only if G is finitely generated as a pro-p group. And, G is of type
$FP_1$
if and only if G is finitely generated as a pro-p group. And, G is of type
![]() $FP_2$
if and only if G is finitely presented as a pro-p group, i.e.,
$FP_2$
if and only if G is finitely presented as a pro-p group, i.e.,
![]() $G \simeq F/ R$
, where F is a free pro-p group with a finite free basis X and R is the smallest normal pro-p subgroup of F that contains some fixed finite set of relations of G. It is interesting to note that for abstract (discrete) groups, the abstract versions of the properties
$G \simeq F/ R$
, where F is a free pro-p group with a finite free basis X and R is the smallest normal pro-p subgroup of F that contains some fixed finite set of relations of G. It is interesting to note that for abstract (discrete) groups, the abstract versions of the properties
![]() $FP_2$
and finite presentability do not coincide [Reference Bestvina and Brady3].
$FP_2$
and finite presentability do not coincide [Reference Bestvina and Brady3].
In this paper, we develop results on algebraic fibering and coherence of pro-p groups. The case of abstract groups was considered by Kochloukova and Vidussi in [Reference Kochloukova and Vidussi13], where the authors used specific techniques from geometric group theory, namely the Bieri–Neumann–Renz–Strebel
![]() $\Sigma $
-invariants. We will use the pro-p version of the
$\Sigma $
-invariants. We will use the pro-p version of the
![]() $\Sigma ^1$
-invariant, suggested in [Reference King10] for pro-p metabelian groups, only in the proof of Proposition 3.4 and most of the results in this paper would have purely homological proofs. We note that the results on incoherence we obtain are quite general and in their full generality are not known for abstract groups (see Corollaries 1.3 and 1.4).
$\Sigma ^1$
-invariant, suggested in [Reference King10] for pro-p metabelian groups, only in the proof of Proposition 3.4 and most of the results in this paper would have purely homological proofs. We note that the results on incoherence we obtain are quite general and in their full generality are not known for abstract groups (see Corollaries 1.3 and 1.4).
Theorem 1.1 Let
![]() $1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups and let
$1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups and let
![]() $n_0 \geq 1$
be an integer such that:
$n_0 \geq 1$
be an integer such that:
1) G and K are of type
![]() $FP_{n_0}$
,
$FP_{n_0}$
,
2)
![]() $\Gamma ^{ab}$
is infinite,
$\Gamma ^{ab}$
is infinite,
3) there is a normal pro-p subgroup N of K such that
![]() $G'\cap K \subseteq N$
,
$G'\cap K \subseteq N$
,
![]() $K/ N \simeq \mathbb {Z}_p$
and N is of type
$K/ N \simeq \mathbb {Z}_p$
and N is of type
![]() $FP_{n_0-1}$
.
$FP_{n_0-1}$
.
Then there is a normal pro-p subgroup M of G such that
![]() $G/ M \simeq \mathbb {Z}_p$
,
$G/ M \simeq \mathbb {Z}_p$
,
![]() $M \cap K = N$
, and M is of type
$M \cap K = N$
, and M is of type
![]() $FP_{n_0}$
. Furthermore, if K, G, and N are of type
$FP_{n_0}$
. Furthermore, if K, G, and N are of type
![]() $FP_{\infty }$
, then M can be chosen of type
$FP_{\infty }$
, then M can be chosen of type
![]() $FP_{\infty }$
.
$FP_{\infty }$
.
We call a discrete pro-p character of G a nontrivial homomorphism of pro-p groups
![]() $\alpha : G \to H$
such that
$\alpha : G \to H$
such that
![]() $H \simeq \mathbb {Z}_p$
. Then Theorem 1.1 could be restated as: assume that G and K are of type
$H \simeq \mathbb {Z}_p$
. Then Theorem 1.1 could be restated as: assume that G and K are of type
![]() $FP_{n_0}$
,
$FP_{n_0}$
,
![]() $\Gamma ^{ab}$
is infinite, and there is a discrete pro-p character
$\Gamma ^{ab}$
is infinite, and there is a discrete pro-p character
![]() $\alpha $
of G such that
$\alpha $
of G such that
![]() $\alpha | _K \not = 0$
,
$\alpha | _K \not = 0$
,
![]() $\mathrm{Ker}(\alpha ) \cap K = N$
is of type
$\mathrm{Ker}(\alpha ) \cap K = N$
is of type
![]() $FP_{n_0-1}$
. Then there exists a discrete pro-p character
$FP_{n_0-1}$
. Then there exists a discrete pro-p character
![]() $\mu $
of G such that
$\mu $
of G such that
![]() $M = \mathrm{Ker}(\mu )$
is of type
$M = \mathrm{Ker}(\mu )$
is of type
![]() $FP_{n_0}$
and
$FP_{n_0}$
and
![]() $\mu |_K = \alpha |_K$
, in particular
$\mu |_K = \alpha |_K$
, in particular
![]() $M \cap K = N$
.
$M \cap K = N$
.
There is a lot in the literature on coherent abstract groups (see, for example, [Reference Wise27]), but very little is known for coherent pro-p groups. Similar to the abstract case, a pro-p group G is coherent (in the category of pro-p groups) if every finitely generated pro-p subgroup of G is finitely presented as a pro-p group, i.e., is of type
![]() $FP_2$
. We generalize this concept and define that a pro-p group G is n-coherent if any pro-p subgroup of G that is of type
$FP_2$
. We generalize this concept and define that a pro-p group G is n-coherent if any pro-p subgroup of G that is of type
![]() $FP_n$
is of type
$FP_n$
is of type
![]() $FP_{n+1}$
. Thus, a pro-p group is 1-coherent if and only if it is coherent (in the category of pro-p groups).
$FP_{n+1}$
. Thus, a pro-p group is 1-coherent if and only if it is coherent (in the category of pro-p groups).
Corollary 1.2 Let K,
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $G = K \rtimes \Gamma $
be pro-p groups and let
$G = K \rtimes \Gamma $
be pro-p groups and let
![]() $n_0 \geq 1$
be an integer such that:
$n_0 \geq 1$
be an integer such that:
1)
![]() $\Gamma $
is finitely generated free pro-p but not pro-p cyclic,
$\Gamma $
is finitely generated free pro-p but not pro-p cyclic,
2) K is of type
![]() $FP_{n_0}$
,
$FP_{n_0}$
,
3) there is a normal pro-p subgroup N of K such that
![]() $G'\cap K \subseteq N$
,
$G'\cap K \subseteq N$
,
![]() $K/ N \simeq \mathbb {Z}_p$
and N is of type
$K/ N \simeq \mathbb {Z}_p$
and N is of type
![]() $FP_{n_0 -1}$
but is not of type
$FP_{n_0 -1}$
but is not of type
![]() $FP_{n_0}$
.
$FP_{n_0}$
.
Then there is a normal pro-p subgroup M of G such that
![]() $G/ M \simeq \mathbb {Z}_p$
,
$G/ M \simeq \mathbb {Z}_p$
,
![]() $M \cap K = N$
, and M is of type
$M \cap K = N$
, and M is of type
![]() $FP_{n_0}$
but is not of type
$FP_{n_0}$
but is not of type
![]() $FP_{n_0 + 1}$
. In particular, G is not
$FP_{n_0 + 1}$
. In particular, G is not
![]() $n_0$
-coherent.
$n_0$
-coherent.
As in the case of Theorem 1.1, Corollary 1.2 can be restated in terms of discrete pro-p characters.
We say that a group is incoherent if it is not coherent. The following result can be deduced from Theorem 3.6, that follows from Corollary 1.2.
Corollary 1.3 Let
![]() $ 1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups such that:
$ 1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups such that:
1) K is a finitely generated pro-p group,
2) there is a normal pro-p subgroup N of K with
![]() $K/ N \simeq \mathbb {Z}_p$
and N is not finitely generated,
$K/ N \simeq \mathbb {Z}_p$
and N is not finitely generated,
3)
![]() $\Gamma $
contains a non-abelian free pro-p subgroup.
$\Gamma $
contains a non-abelian free pro-p subgroup.
Then G is incoherent (in the category of pro-p groups).
The class of pro-p groups
![]() $\mathcal {L}$
was first considered by Kochloukova and Zalesskii in [Reference Kochloukova and Zalesskii14]. It contains all finitely generated free pro-p groups, and its profinite version was considered by Zalesskii and Zapata in [Reference Zalesskii and Zapata28]. A pro-p group from
$\mathcal {L}$
was first considered by Kochloukova and Zalesskii in [Reference Kochloukova and Zalesskii14]. It contains all finitely generated free pro-p groups, and its profinite version was considered by Zalesskii and Zapata in [Reference Zalesskii and Zapata28]. A pro-p group from
![]() $\mathcal {L}$
shares many properties with an abstract limit group, in particular it is defined using extensions of centralizers. Still there are many open questions about the class of pro-p groups
$\mathcal {L}$
shares many properties with an abstract limit group, in particular it is defined using extensions of centralizers. Still there are many open questions about the class of pro-p groups
![]() $\mathcal {L}$
. For example, by Wilton’s result from [Reference Wilton26], every finitely generated subgroup of an abstract limit group is a virtual retract, but the pro-p version of this result is still an open problem.
$\mathcal {L}$
. For example, by Wilton’s result from [Reference Wilton26], every finitely generated subgroup of an abstract limit group is a virtual retract, but the pro-p version of this result is still an open problem.
For a pro-p group K, we write
![]() $d(K)$
for the cardinality of a minimal set of (topological) generators, i.e.,
$d(K)$
for the cardinality of a minimal set of (topological) generators, i.e.,
![]() $d(K) = \dim _{\mathbb {F}_p} H_1(K, \mathbb {F}_p)$
.
$d(K) = \dim _{\mathbb {F}_p} H_1(K, \mathbb {F}_p)$
.
Corollary 1.4 Let
![]() $ 1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups such that:
$ 1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups such that:
1) K is a non-abelian pro-p group from the class
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
2)
![]() $\Gamma $
contains a non-abelian, free pro-p subgroup.
$\Gamma $
contains a non-abelian, free pro-p subgroup.
Then G is incoherent (in the category of pro-p groups). In particular, if K is a finitely generated free pro-p group with
![]() $d(K) \geq 2$
, then G is incoherent (in the category of pro-p groups).
$d(K) \geq 2$
, then G is incoherent (in the category of pro-p groups).
We note that the version of Corollary 1.4 for abstract groups is still open even when K and
![]() $\Gamma $
are free, non-abelian with K of rank at least 3. The same holds for Corollary 1.3.
$\Gamma $
are free, non-abelian with K of rank at least 3. The same holds for Corollary 1.3.
It is known that abstract (free finite rank)-by-
![]() $\mathbb {Z}$
groups are coherent [Reference Feign and Handel8]. There is a conjecture suggested by Wise and independently by Kropholler and Walsh that an abstract (free of finite rank
$\mathbb {Z}$
groups are coherent [Reference Feign and Handel8]. There is a conjecture suggested by Wise and independently by Kropholler and Walsh that an abstract (free of finite rank
![]() $\geq 2$
)-by-(free of finite rank
$\geq 2$
)-by-(free of finite rank
![]() $\geq 2$
) group is incoherent (see [Reference Kropholler and Walsh15]). The conjecture was proved in [Reference Kropholler and Walsh15] for a (free of rank 2)-by-(free of finite rank
$\geq 2$
) group is incoherent (see [Reference Kropholler and Walsh15]). The conjecture was proved in [Reference Kropholler and Walsh15] for a (free of rank 2)-by-(free of finite rank
![]() $\geq 2$
) abstract group, with a proof that cannot be modified for pro-p groups. By Corollary 1.4, a pro-p version of this result holds too.
$\geq 2$
) abstract group, with a proof that cannot be modified for pro-p groups. By Corollary 1.4, a pro-p version of this result holds too.
A pro-p right angled Artin group (pro-p RAAG) associated with a finite simplicial graph X can be defined either as the pro-p completion of the abstract RAAG associated with X or by the same presentation as the abstract RAAG associated with X but in the category of pro-p groups.
Demushkin groups are some special, finitely generated, 1-related pro-p groups. The pro-p completion of an orientable surface group is a Demushkin pro-p group, but there are Demushkin pro-p groups that are not obtained this way. There are several types of Demushkin pro-p groups completely described in terms of presentations in [Reference Demushkin5, Reference Demushkin6, Reference Labute17, Reference Serre23]. The following corollary provides many examples where Theorem 1.1 and Corollary 1.3 apply.
Corollary 1.5 Let
![]() $1\to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups such that:
$1\to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups such that:
1) K is a non-abelian pro-p RAAG or a non-soluble Demushkin group,
2)
![]() $\Gamma $
is a non-abelian pro-p RAAG or a non-soluble Demushkin group.
$\Gamma $
is a non-abelian pro-p RAAG or a non-soluble Demushkin group.
Then G is incoherent (in the category of pro-p groups).
For a finite rank free pro-p group F, the structure of
![]() $\mathrm{Aut}(F)$
was studied first by Lubotsky in [Reference Lubotzky18].
$\mathrm{Aut}(F)$
was studied first by Lubotsky in [Reference Lubotzky18].
![]() $\mathrm{Aut}(F)$
is a topological group with a pro-p subgroup of finite index. In [Reference Gordon9], Gordon proved that the automorphism group of an abstract free group of rank 2 is incoherent. Unfortunately we could not prove a pro-p version of this result, but still it would hold if the group of outer pro-p automorphisms of a free pro-p group of rank 2 contains a free non-procyclic pro-p subgroup. For a free abstract group
$\mathrm{Aut}(F)$
is a topological group with a pro-p subgroup of finite index. In [Reference Gordon9], Gordon proved that the automorphism group of an abstract free group of rank 2 is incoherent. Unfortunately we could not prove a pro-p version of this result, but still it would hold if the group of outer pro-p automorphisms of a free pro-p group of rank 2 contains a free non-procyclic pro-p subgroup. For a free abstract group
![]() $F_2$
of rank 2, we have that
$F_2$
of rank 2, we have that
![]() $\mathrm{Out}(F_2) \simeq GL_2(\mathbb {Z})$
; hence,
$\mathrm{Out}(F_2) \simeq GL_2(\mathbb {Z})$
; hence,
![]() $\mathrm{Out}(F_2)$
contains a free non-cyclic abstract group. Nevertheless, the group
$\mathrm{Out}(F_2)$
contains a free non-cyclic abstract group. Nevertheless, the group
![]() $GL_2^1(\mathbb {Z}_p) = \mathrm{Ker} (GL_2(\mathbb {Z}_p) \to GL_2(\mathbb {F}_p))$
does not contain a free pro-p non-procyclic pro-p subgroup, since it is p-adic analytic and so there is an upper limit on the number of generators of finitely generated pro-p subgroups [Reference Dixon, Du Sautoy, Mann and Segal7]. For related results on non-existence of free pro-p subgroups in matrix groups, see [Reference Barnea and Larsen1, Reference Ben-Ezra and Zelmanov2, Reference Zubkov29].
$GL_2^1(\mathbb {Z}_p) = \mathrm{Ker} (GL_2(\mathbb {Z}_p) \to GL_2(\mathbb {F}_p))$
does not contain a free pro-p non-procyclic pro-p subgroup, since it is p-adic analytic and so there is an upper limit on the number of generators of finitely generated pro-p subgroups [Reference Dixon, Du Sautoy, Mann and Segal7]. For related results on non-existence of free pro-p subgroups in matrix groups, see [Reference Barnea and Larsen1, Reference Ben-Ezra and Zelmanov2, Reference Zubkov29].
Let G be a finitely generated pro-p group. Define
![]() $\mathrm{Aut}_0(G) = \mathrm{Ker} (\mathrm{Aut}(G) \to \mathrm{Aut}(G/ G^*)),$
where
$\mathrm{Aut}_0(G) = \mathrm{Ker} (\mathrm{Aut}(G) \to \mathrm{Aut}(G/ G^*)),$
where
![]() $G^*$
is the Frattini subgroup of G. Then
$G^*$
is the Frattini subgroup of G. Then
![]() $\mathrm{Aut}_0(G)$
is a pro-p subgroup of
$\mathrm{Aut}_0(G)$
is a pro-p subgroup of
![]() $\mathrm{Aut}(G)$
of finite index.
$\mathrm{Aut}(G)$
of finite index.
Corollary 1.6 Suppose that K is a finitely generated free pro-p group with
![]() $ d(K) \geq 2$
. If
$ d(K) \geq 2$
. If
![]() $\mathrm{Out}(K)$
contains a pro-p free non-procyclic subgroup, then
$\mathrm{Out}(K)$
contains a pro-p free non-procyclic subgroup, then
![]() $\mathrm{Aut}_0(K)$
is incoherent (in the category of pro-p groups).
$\mathrm{Aut}_0(K)$
is incoherent (in the category of pro-p groups).
By the Bieri–Strebel results in [Reference Bieri and Strebel4] for a finitely presented abstract group H that does not contain free non-cyclic abstract subgroups, every metabelian quotient of H is finitely presented. It is an open question whether a pro-p version of the Bieri–Strebel result holds, i.e., whether if G is a finitely presented pro-p group without free non-procyclic pro-p subgroups, then every metabelian pro-p quotient of G is finitely presented as a pro-p group. Note that by the King classification of the finitely presented metabelian pro-p groups in [Reference King11], every pro-p quotient of a finitely presented metabelian pro-p group is finitely presented pro-p. Using Corollary 1.6 and some ideas introduced by Romankov in [Reference Romankov21, Reference Romankov22], we prove the following result.
Corollary 1.7 Suppose that K is a finitely generated free pro-p group with
![]() $d(K) \geq 2$
. Then either
$d(K) \geq 2$
. Then either
![]() $\mathrm{Aut}_0(K)$
is incoherent (in the category of pro-p groups) or the pro-p version of the Bieri–Strebel result does not hold.
$\mathrm{Aut}_0(K)$
is incoherent (in the category of pro-p groups) or the pro-p version of the Bieri–Strebel result does not hold.
2 Preliminaries
2.1 Homological finiteness properties of pro-p groups
Let G be a pro-p group. By definition,
 $$ \begin{align*}\mathbb{Z}_p[[G]] = {\varprojlim} \frac{\mathbb{Z}}{p^i \mathbb{Z}} [[G/ U]],\end{align*} $$
$$ \begin{align*}\mathbb{Z}_p[[G]] = {\varprojlim} \frac{\mathbb{Z}}{p^i \mathbb{Z}} [[G/ U]],\end{align*} $$
where the inverse limit is over all
![]() $i \geq 1$
and U open subgroups of G. And,
$i \geq 1$
and U open subgroups of G. And,
where the inverse limit is over all open subgroups U of G.
By definition, the pro-p group G is of type
![]() $FP_m$
if the trivial
$FP_m$
if the trivial
![]() $\mathbb {Z}_p[[G]]$
-module
$\mathbb {Z}_p[[G]]$
-module
![]() $\mathbb {Z}_p$
has a projective resolution where all projectives in dimension
$\mathbb {Z}_p$
has a projective resolution where all projectives in dimension
![]() $\leq m$
are finitely generated
$\leq m$
are finitely generated
![]() $\mathbb {Z}_p[[G]]$
-modules, i.e., there is an exact complex of pro-
$\mathbb {Z}_p[[G]]$
-modules, i.e., there is an exact complex of pro-
![]() $p\ \mathbb {Z}_p[[G]]$
-modules
$p\ \mathbb {Z}_p[[G]]$
-modules
where each
![]() $P_i$
projective and for
$P_i$
projective and for
![]() $i \leq m$
we have that
$i \leq m$
we have that
![]() $P_i$
is finitely generated.
$P_i$
is finitely generated.
Such resolutions can be used to compute the pro-p homology groups
![]() $H_i(G, - )$
. Suppose V is a left pro-
$H_i(G, - )$
. Suppose V is a left pro-
![]() $p\ \mathbb {Z}_p[[G]]$
-module and
$p\ \mathbb {Z}_p[[G]]$
-module and
![]() $\mathcal {P}$
is a complex of right pro-
$\mathcal {P}$
is a complex of right pro-
![]() $p\ \mathbb {Z}_p[[G]]$
-modules. Then the pro-p homology group
$p\ \mathbb {Z}_p[[G]]$
-modules. Then the pro-p homology group
![]() $H_i(G, V)$
is defined as
$H_i(G, V)$
is defined as
 $H_i( {\mathcal P}^{\mathrm{del}} \otimes _{\mathbb {Z}_p[[G]]} V)$
. If W is a discrete right G-module, the cohomology group
$H_i( {\mathcal P}^{\mathrm{del}} \otimes _{\mathbb {Z}_p[[G]]} V)$
. If W is a discrete right G-module, the cohomology group
![]() $H^i(G, W)$
is defined as
$H^i(G, W)$
is defined as
![]() $H^i (\mathrm{Hom}_G({\mathcal {P}}^{\mathrm{del}}, W))$
. Here,
$H^i (\mathrm{Hom}_G({\mathcal {P}}^{\mathrm{del}}, W))$
. Here,
![]() $\mathcal {P}^{\mathrm{del}}$
denotes the deleted resolution obtained from
$\mathcal {P}^{\mathrm{del}}$
denotes the deleted resolution obtained from
![]() $\mathcal {P}$
by deleting the module
$\mathcal {P}$
by deleting the module
![]() $\mathbb {Z}_p$
from dimension
$\mathbb {Z}_p$
from dimension
![]() $-1$
, i.e., substituting it with the zero module and
$-1$
, i.e., substituting it with the zero module and
![]() $\mathrm{Hom}_G$
denotes continuous G-homomorphisms. For more on homology and cohomology of pro-p groups, see [Reference Ribes and Zalesskii20, Reference Wilson25].
$\mathrm{Hom}_G$
denotes continuous G-homomorphisms. For more on homology and cohomology of pro-p groups, see [Reference Ribes and Zalesskii20, Reference Wilson25].
By [Reference King10], for a pro-p group, the following conditions are equivalent:
1) G is of type
![]() $FP_m$
;
$FP_m$
;
2)
![]() $H_i(G, \mathbb {Z}_p)$
is a finitely generated (abelian) pro-p group for
$H_i(G, \mathbb {Z}_p)$
is a finitely generated (abelian) pro-p group for
![]() $i \leq m$
;
$i \leq m$
;
3)
![]() $H_i(G, \mathbb {F}_p)$
is finite for
$H_i(G, \mathbb {F}_p)$
is finite for
![]() $i \leq m$
;
$i \leq m$
;
4) for K either
![]() $\mathbb {F}_p$
or
$\mathbb {F}_p$
or
![]() $\mathbb {Z}_p$
and N a normal pro-p subgroup of G such that
$\mathbb {Z}_p$
and N a normal pro-p subgroup of G such that
![]() $K[[G/N]]$
is left and right Noetherian, the homology groups
$K[[G/N]]$
is left and right Noetherian, the homology groups
![]() $H_i(N, K)$
are finitely generated as pro-
$H_i(N, K)$
are finitely generated as pro-
![]() $p\ K[[G/N]]$
-modules for all
$p\ K[[G/N]]$
-modules for all
![]() $i \leq m$
, where the
$i \leq m$
, where the
![]() $G/N$
action is induced by the conjugation action of G on N.
$G/N$
action is induced by the conjugation action of G on N.
The equivalence of the above conditions is a corollary of the fact that
![]() $\mathbb {Z}_p[[G]]$
and
$\mathbb {Z}_p[[G]]$
and
![]() $\mathbb {F}_p[[G]]$
are local rings. Furthermore, in 3)
$\mathbb {F}_p[[G]]$
are local rings. Furthermore, in 3)
![]() $H_i(G, \mathbb {F}_p)$
could be substituted with
$H_i(G, \mathbb {F}_p)$
could be substituted with
![]() $H^i(G, \mathbb {F}_p)$
.
$H^i(G, \mathbb {F}_p)$
.
2.2 The King invariant
Let Q be a finitely generated abelian pro-p group, and let
![]() $\mathbb {F}$
be the algebraic closure of
$\mathbb {F}$
be the algebraic closure of
![]() $\mathbb {F}_p$
. Denote by
$\mathbb {F}_p$
. Denote by
![]() $\mathbb {F}[[t]]^{\times }$
the multiplicative group of invertible elements in
$\mathbb {F}[[t]]^{\times }$
the multiplicative group of invertible elements in
![]() $\mathbb {F} [[t]]$
. Consider
$\mathbb {F} [[t]]$
. Consider
where
![]() $\mathbb {F}[[t]]^{\times } $
is a topological group with topology induced by the topology of the ring
$\mathbb {F}[[t]]^{\times } $
is a topological group with topology induced by the topology of the ring
![]() $\mathbb {F}[[t]]$
, given by the sequence of ideals
$\mathbb {F}[[t]]$
, given by the sequence of ideals
![]() $(t) \supseteq (t^2) \supseteq \cdots \supseteq (t^i) \supseteq \cdots $
. Note that since
$(t) \supseteq (t^2) \supseteq \cdots \supseteq (t^i) \supseteq \cdots $
. Note that since
![]() $\chi $
is continuous, we have that
$\chi $
is continuous, we have that
For
![]() $\chi \in T(Q)$
, there is a unique continuous ring homomorphism
$\chi \in T(Q)$
, there is a unique continuous ring homomorphism
that extends
![]() $\chi $
.
$\chi $
.
Let A be a finitely generated pro-
![]() $p\ \mathbb {Z}_p[[Q]]$
-module. In [Reference King11], King defined the following invariant:
$p\ \mathbb {Z}_p[[Q]]$
-module. In [Reference King11], King defined the following invariant:
In [Reference King11], King used the notation
![]() $\Xi (A)$
, that we here substitute by
$\Xi (A)$
, that we here substitute by
![]() $\Delta (A)$
.
$\Delta (A)$
.
Let P be a pro-p subgroup of Q. Define
Theorem 2.1 [Reference King11, Theorem B], [Reference King11, Lemma 2.5]
Let Q be a finitely generated abelian pro-p group. Let A be a finitely generated pro-
![]() $p\ \mathbb {Z}_p[[Q]]$
-module.
$p\ \mathbb {Z}_p[[Q]]$
-module.
a) Then A is finitely generated as an abelian pro-p group if and only if
![]() $\Delta (A) = \{ 1 \}$
.
$\Delta (A) = \{ 1 \}$
.
b) If P is a pro-p subgroup of Q, then
In particular, A is finitely generated as a pro-
![]() $p\ \mathbb {Z}_p[[P]]$
-module if and only if
$p\ \mathbb {Z}_p[[P]]$
-module if and only if
![]() $T(Q, P) \cap \Delta (A) = \{1 \}$
.
$T(Q, P) \cap \Delta (A) = \{1 \}$
.
We state the classification of the finitely presented metabelian pro-p groups given by King in [Reference King11].
Theorem 2.2 [Reference King11]
Let
![]() $1 \to A \to G \to Q \to 1$
be a short exact sequence of pro-p groups, where G is a finitely generated pro-p group and A and Q are abelian. Then G is a finitely presented pro-p group if and only if
$1 \to A \to G \to Q \to 1$
be a short exact sequence of pro-p groups, where G is a finitely generated pro-p group and A and Q are abelian. Then G is a finitely presented pro-p group if and only if
![]() $\Delta (A) \cap \Delta (A)^{-1} = \{ 1 \}$
.
$\Delta (A) \cap \Delta (A)^{-1} = \{ 1 \}$
.
Example Let
![]() $A = \mathbb {F}_p[[s]]$
,
$A = \mathbb {F}_p[[s]]$
,
![]() $Q = \mathbb {Z}_p $
,
$Q = \mathbb {Z}_p $
,
![]() $G = A \rtimes Q$
, where
$G = A \rtimes Q$
, where
![]() $Q = \mathbb {Z}_p$
has a generator b and b acts via conjugation on A by multiplication with
$Q = \mathbb {Z}_p$
has a generator b and b acts via conjugation on A by multiplication with
![]() $1 + s$
. Since
$1 + s$
. Since
we conclude that
![]() $\Delta (A) = T(Q) = \Delta (A) ^{-1}$
. Hence, by Theorem 2.2, G is not finitely presented (as a pro-p group).
$\Delta (A) = T(Q) = \Delta (A) ^{-1}$
. Hence, by Theorem 2.2, G is not finitely presented (as a pro-p group).
Alternatively, it could be shown by a homological argument that if
![]() $1 \to A \to G \to Q \to 1$
is a short exact sequence of pro-p groups, where G is finitely presented and A and Q are abelian, then the pro-p homology group
$1 \to A \to G \to Q \to 1$
is a short exact sequence of pro-p groups, where G is finitely presented and A and Q are abelian, then the pro-p homology group
![]() $H_2(A, \mathbb {Z}_p) \simeq A \widehat {\wedge }_{\mathbb {Z}_p} A$
is finitely generated as
$H_2(A, \mathbb {Z}_p) \simeq A \widehat {\wedge }_{\mathbb {Z}_p} A$
is finitely generated as
![]() $\mathbb {Z}_p[[Q]]$
-module, where
$\mathbb {Z}_p[[Q]]$
-module, where
![]() $\widehat {\wedge }$
denotes completed exterior product. In our example, the last condition fails, so G is not finitely presented (as a pro-p group).
$\widehat {\wedge }$
denotes completed exterior product. In our example, the last condition fails, so G is not finitely presented (as a pro-p group).
2.3 Demushkin pro-p groups
Following [Reference Serre24], a Demushkin group G is a Poincare duality group of dimension 2, i.e.,
![]() $H^i(G, \mathbb {F}_p)$
is finite for all i,
$H^i(G, \mathbb {F}_p)$
is finite for all i,
![]() $\dim H^2(G, \mathbb {F}_p) = 1$
and the cup product
$\dim H^2(G, \mathbb {F}_p) = 1$
and the cup product
is a non-degenerated bilinear form for all
![]() $i \geq 0$
. In particular, the cohomological dimension of G is
$i \geq 0$
. In particular, the cohomological dimension of G is ![]() .
.
There are two invariants associated with a Demushkin pro-p group: the minimal number of (topological) generators d and q that is either a power of the prime p or
![]() $\infty $
. We state several results from [Reference Demushkin5, Reference Demushkin6, Reference Labute17, Reference Serre23] that classify the Demushkin pro-p groups. Other excellent reference for Demushkin pro-p groups is [Reference Wilson25].
$\infty $
. We state several results from [Reference Demushkin5, Reference Demushkin6, Reference Labute17, Reference Serre23] that classify the Demushkin pro-p groups. Other excellent reference for Demushkin pro-p groups is [Reference Wilson25].
Theorem 2.3 [Reference Demushkin5, Reference Demushkin6]
Let D be a Demushkin group with invariants
![]() $d, q$
and suppose that
$d, q$
and suppose that
![]() $q \not = 2$
. Then d is even and D is isomorphic to
$q \not = 2$
. Then d is even and D is isomorphic to
![]() $F /R$
, where F is a free pro-p group with basis
$F /R$
, where F is a free pro-p group with basis
![]() $x_1, \ldots , x_d$
and R is generated as a normal closed subgroup by
$x_1, \ldots , x_d$
and R is generated as a normal closed subgroup by
where for
![]() $q = \infty $
we define
$q = \infty $
we define
![]() $x_1^{\infty } = 1$
. Furthermore, all groups having such presentations are Demushkin.
$x_1^{\infty } = 1$
. Furthermore, all groups having such presentations are Demushkin.
Theorem 2.4 [Reference Serre23]
Let D be a Demushkin pro-
![]() $2$
group with invariants
$2$
group with invariants
![]() $d, q$
and suppose that
$d, q$
and suppose that
![]() $q = 2$
and d is odd. Then D is isomorphic to
$q = 2$
and d is odd. Then D is isomorphic to
![]() $F /R$
, where F is a free pro-
$F /R$
, where F is a free pro-
![]() $2$
group with basis
$2$
group with basis
![]() $x_1, \ldots , x_d$
and R is generated as a normal closed subgroup by
$x_1, \ldots , x_d$
and R is generated as a normal closed subgroup by
for some integer
![]() $f \geq 2$
or
$f \geq 2$
or
![]() $\infty $
. Furthermore, all groups having such presentations are Demushkin.
$\infty $
. Furthermore, all groups having such presentations are Demushkin.
Theorem 2.5 [Reference Labute17]
Let D be a Demushkin pro-
![]() $2$
group with d even and
$2$
group with d even and
![]() $q = 2$
. Then D is isomorphic to
$q = 2$
. Then D is isomorphic to
![]() $F /R$
, where F is a free pro-
$F /R$
, where F is a free pro-
![]() $2$
group with basis
$2$
group with basis
![]() $x_1, \ldots , x_d$
and R is generated as a normal closed subgroup either by
$x_1, \ldots , x_d$
and R is generated as a normal closed subgroup either by
for some integer
![]() $f \geq 2$
or
$f \geq 2$
or
![]() $f = \infty $
, or by
$f = \infty $
, or by
for some integer
![]() $f \geq 2$
or
$f \geq 2$
or
![]() $f = \infty $
,
$f = \infty $
,
![]() $d \geq 4$
. Furthermore, all groups having such presentations are Demushkin.
$d \geq 4$
. Furthermore, all groups having such presentations are Demushkin.
3 Proofs of the main results
The following result is a pro-p version of results from [Reference Kochloukova and Lima12, Reference Kuckuck16], where homotopical and homological versions for discrete groups are considered.
Lemma 3.1 Let
![]() $n \geq 1$
be a natural number,
$n \geq 1$
be a natural number,
a short exact sequence of pro-p groups with A of type
![]() $FP_n$
and C of type
$FP_n$
and C of type
![]() $FP_{n+1}$
. Assume that there is another short exact sequence of pro-p groups
$FP_{n+1}$
. Assume that there is another short exact sequence of pro-p groups
with
![]() $B_0$
of type
$B_0$
of type
![]() $FP_{n+1}$
and that there is a homomorphism of pro-p groups
$FP_{n+1}$
and that there is a homomorphism of pro-p groups
![]() $\theta : B_0 \rightarrow B$
such that
$\theta : B_0 \rightarrow B$
such that
![]() $\theta |_A = id_A$
, i.e., there is a commutative diagram of homomorphisms of pro-p groups
$\theta |_A = id_A$
, i.e., there is a commutative diagram of homomorphisms of pro-p groups

Then B is of type
![]() $FP_{n+1}$
.
$FP_{n+1}$
.
Remark
![]() $\theta $
does not need to be injective or surjective.
$\theta $
does not need to be injective or surjective.
Proof Consider the LHS spectral sequence
Similarly there is an LHS spectral sequence
Since A is of type
![]() $FP_n$
, we have that
$FP_n$
, we have that
![]() $H_j(A, \mathbb {F}_p)$
is finite for all
$H_j(A, \mathbb {F}_p)$
is finite for all
![]() $j \leq n$
. Then there is a pro-p subgroup
$j \leq n$
. Then there is a pro-p subgroup
![]() $C_1$
of finite index in C such that
$C_1$
of finite index in C such that
![]() $C_1$
acts trivially on
$C_1$
acts trivially on
![]() $H_j(A, \mathbb {F}_p)$
for every
$H_j(A, \mathbb {F}_p)$
for every
![]() $j \leq n$
. Since C is of type
$j \leq n$
. Since C is of type
![]() $FP_{n+1}$
, we have that
$FP_{n+1}$
, we have that
![]() $C_1$
is of type
$C_1$
is of type
![]() $FP_{n+1}$
. Then
$FP_{n+1}$
. Then
where we have
![]() $\dim _{\mathbb {F}_p} H_j(A, \mathbb {F}_p)$
direct summands in the right-hand side of the above isomorphism. Since
$\dim _{\mathbb {F}_p} H_j(A, \mathbb {F}_p)$
direct summands in the right-hand side of the above isomorphism. Since
![]() $C_1$
has finite index in C, we deduce that
$C_1$
has finite index in C, we deduce that
hence by the convergence of the second spectral sequence, we obtain that
Note that we have shown that if
![]() $i + j = n+1 , i \not = 0$
, then
$i + j = n+1 , i \not = 0$
, then
![]() $\widehat {E}_{i,j}^2$
is finite, and hence
$\widehat {E}_{i,j}^2$
is finite, and hence
![]() $\widehat {E}_{i,j}^{\infty }$
is finite. By the convergence of the spectral sequence, there is a filtration of
$\widehat {E}_{i,j}^{\infty }$
is finite. By the convergence of the spectral sequence, there is a filtration of
![]() $H_{n+1}(B, \mathbb {F}_p)$
$H_{n+1}(B, \mathbb {F}_p)$
where
![]() $ F_{i}(H_{n+1}(B, \mathbb {F}_p)) / F_{i-1}(H_{n+1}(B, \mathbb {F}_p)) \simeq \widehat {E}_{i, n+1 - i}^{ \infty }$
. Thus,
$ F_{i}(H_{n+1}(B, \mathbb {F}_p)) / F_{i-1}(H_{n+1}(B, \mathbb {F}_p)) \simeq \widehat {E}_{i, n+1 - i}^{ \infty }$
. Thus,
Note that since any differential that comes out from
![]() $\widehat {E}^r_{0, n+1}$
is zero, we have that
$\widehat {E}^r_{0, n+1}$
is zero, we have that
![]() $\widehat {E}_{0,n+1}^{\infty }$
is a quotient of
$\widehat {E}_{0,n+1}^{\infty }$
is a quotient of
![]() $\widehat {E}^2_{0, n+1} = H_0(C, H_{n+1}(A, \mathbb {F}_p))$
, and thus there is a map
$\widehat {E}^2_{0, n+1} = H_0(C, H_{n+1}(A, \mathbb {F}_p))$
, and thus there is a map
with image that equals
![]() $\widehat {E}^{ \infty }_{0, n+1}$
. Thus,
$\widehat {E}^{ \infty }_{0, n+1}$
. Thus,
Similarly, there is a map
with image that equals
![]() ${E}^{ \infty }_{0, n+1}$
and such that
${E}^{ \infty }_{0, n+1}$
and such that
![]() $B_0$
is of type
$B_0$
is of type
![]() $FP_{n+1}$
if and only if
$FP_{n+1}$
if and only if
![]() $\mathrm{Im} (\mu _0)$
is finite. Since
$\mathrm{Im} (\mu _0)$
is finite. Since
![]() $B_0$
is of type
$B_0$
is of type
![]() $FP_{n+1}$
, we conclude that
$FP_{n+1}$
, we conclude that
![]() $\mathrm{Im} (\mu _0)$
is finite.
$\mathrm{Im} (\mu _0)$
is finite.
The naturality of the LHS spectral sequence implies that we have the commutative diagram

where the maps
![]() $\rho $
and
$\rho $
and
![]() $\rho _0$
are induced by
$\rho _0$
are induced by
![]() $\nu : C_0 \to C$
and by
$\nu : C_0 \to C$
and by
![]() $\theta $
.
$\theta $
.
Recall that the action of
![]() $B_0$
on A via conjugation induces an action of
$B_0$
on A via conjugation induces an action of
![]() $B_0$
on
$B_0$
on
![]() $H_{n+1}(A, \mathbb {F}_p)$
where A acts trivially and this induces the action of
$H_{n+1}(A, \mathbb {F}_p)$
where A acts trivially and this induces the action of
![]() $C_0$
on
$C_0$
on
![]() $H_{n+1}(A, \mathbb {F}_p)$
that is used to define
$H_{n+1}(A, \mathbb {F}_p)$
that is used to define
![]() $H_0(C_0, H_{n+1}(A, \mathbb {F}_p))$
. Similarly, the action of B on A via conjugation induces an action of B on
$H_0(C_0, H_{n+1}(A, \mathbb {F}_p))$
. Similarly, the action of B on A via conjugation induces an action of B on
![]() $H_{n+1}(A, \mathbb {F}_p)$
where A acts trivially and this induces the action of C on
$H_{n+1}(A, \mathbb {F}_p)$
where A acts trivially and this induces the action of C on
![]() $H_{n+1}(A, \mathbb {F}_p)$
that is used to define
$H_{n+1}(A, \mathbb {F}_p)$
that is used to define
![]() $H_0(C, H_{n+1}(A, \mathbb {F}_p))$
. If
$H_0(C, H_{n+1}(A, \mathbb {F}_p))$
. If
![]() $\nu $
is surjective, then
$\nu $
is surjective, then
![]() $\rho $
is an isomorphism; if
$\rho $
is an isomorphism; if
![]() $\nu $
is injective, then
$\nu $
is injective, then
![]() $\rho $
is surjective. Since every homomorphism
$\rho $
is surjective. Since every homomorphism
![]() $\nu $
is a composition of one epimorphism followed by one monomorphism, we conclude that
$\nu $
is a composition of one epimorphism followed by one monomorphism, we conclude that
![]() $\rho $
is always surjective. Then
$\rho $
is always surjective. Then
Since
![]() $\mathrm{Im} (\mu _0)$
is finite, we conclude that
$\mathrm{Im} (\mu _0)$
is finite, we conclude that
![]() $\mathrm{Im} (\mu )$
is finite. Hence, B is of type
$\mathrm{Im} (\mu )$
is finite. Hence, B is of type
![]() $FP_{n+1}$
as required.
$FP_{n+1}$
as required.
Lemma 3.2 Let
![]() $1 \to A \to B \to C \to 1$
be a short exact sequence of pro-p groups such that for some
$1 \to A \to B \to C \to 1$
be a short exact sequence of pro-p groups such that for some
![]() $m \geq 1$
we have that A is of type
$m \geq 1$
we have that A is of type
![]() $FP_{m-1}$
and B is of type
$FP_{m-1}$
and B is of type
![]() $FP_m$
. Then C is of type
$FP_m$
. Then C is of type
![]() $FP_m$
.
$FP_m$
.
Proof We induct on
![]() $m \geq 1$
. The case
$m \geq 1$
. The case
![]() $m = 1$
is obvious since a pro-p group is of type
$m = 1$
is obvious since a pro-p group is of type
![]() $FP_1$
if and only if the group is finitely generated (as a pro-p group).
$FP_1$
if and only if the group is finitely generated (as a pro-p group).
Assume that
![]() $m> 1$
and that the result holds for
$m> 1$
and that the result holds for
![]() $m-1$
; hence, C is of type
$m-1$
; hence, C is of type
![]() $FP_{m-1}$
. Since A is
$FP_{m-1}$
. Since A is
![]() $FP_{m-1}$
, we have that
$FP_{m-1}$
, we have that
![]() $H_j(A, \mathbb {F}_p)$
is finite for
$H_j(A, \mathbb {F}_p)$
is finite for
![]() $0 \leq j \leq m-1$
. Consider the LHS spectral sequence
$0 \leq j \leq m-1$
. Consider the LHS spectral sequence
By substituting if necessary C with a subgroup of finite index, we can assume that C acts trivially on
![]() $ H_j(A, \mathbb {F}_p)$
for
$ H_j(A, \mathbb {F}_p)$
for
![]() $ 0 \leq j \leq m-1$
. Then
$ 0 \leq j \leq m-1$
. Then
is finite for
![]() $0 \leq i,j \leq m-1$
. Then, for
$0 \leq i,j \leq m-1$
. Then, for
![]() $r \geq 2$
, consider the differential
$r \geq 2$
, consider the differential
and note that either
![]() $m - r < 0$
; hence,
$m - r < 0$
; hence,
![]() $ E_{m-r, r- 1}^2 = 0$
or
$ E_{m-r, r- 1}^2 = 0$
or
![]() $m-r\leq m-1, r- 1 \leq m-1$
. In all cases,
$m-r\leq m-1, r- 1 \leq m-1$
. In all cases,
![]() $E_{m-r, r-1}^2 $
is finite, and hence
$E_{m-r, r-1}^2 $
is finite, and hence
![]() $E_{m-r, r- 1}^r$
is finite and so
$E_{m-r, r- 1}^r$
is finite and so
![]() $E_{m,0}^{r+1}= \mathrm{Ker}(d_{m,0}^r)$
is finite if and only if
$E_{m,0}^{r+1}= \mathrm{Ker}(d_{m,0}^r)$
is finite if and only if
![]() $E_{m,0}^r$
is finite. Thus,
$E_{m,0}^r$
is finite. Thus,
Finally, since B is
![]() $FP_m$
, we have that
$FP_m$
, we have that
![]() $H_m(B, \mathbb {F}_p)$
is finite and by the convergence of the spectral sequence
$H_m(B, \mathbb {F}_p)$
is finite and by the convergence of the spectral sequence
![]() $E_{m,0}^{\infty }$
is finite. Thus, we conclude that
$E_{m,0}^{\infty }$
is finite. Thus, we conclude that
![]() $ H_m(C, \mathbb {F}_p)$
is finite. And, this together with C is of type
$ H_m(C, \mathbb {F}_p)$
is finite. And, this together with C is of type
![]() $FP_{m-1}$
implies that C is
$FP_{m-1}$
implies that C is
![]() $FP_m$
.
$FP_m$
.
Recall that a pro-p HNN extension is called proper if the canonical map from the base group to the pro-p HNN extension is injective.
Lemma 3.3 Let
![]() $G = \langle A, t \ | \ K^t = K \rangle $
be a proper pro-p HNN extension and m is a positive integer. Suppose that M is a normal pro-p subgroup of G such that
$G = \langle A, t \ | \ K^t = K \rangle $
be a proper pro-p HNN extension and m is a positive integer. Suppose that M is a normal pro-p subgroup of G such that
![]() $G/ M \simeq \mathbb {Z}_p$
,
$G/ M \simeq \mathbb {Z}_p$
,
![]() $K \not \subseteq M$
, and
$K \not \subseteq M$
, and
![]() $M \cap A$
is of type
$M \cap A$
is of type
![]() $FP_m$
. Then the following conditions hold:
$FP_m$
. Then the following conditions hold:
a) M is of type
![]() $FP_{m}$
if and only if
$FP_{m}$
if and only if
![]() $M \cap K$
is of type
$M \cap K$
is of type
![]() $FP_{m-1}$
;
$FP_{m-1}$
;
b) if M is of type
![]() $FP_{m+1}$
, then
$FP_{m+1}$
, then
![]() $M \cap K$
is of type
$M \cap K$
is of type
![]() $FP_m$
.
$FP_m$
.
Proof By [Reference Ribes and Zalesskii19, Theorem 4.1], the proper pro-p HNN extension gives rise to the exact sequence of
![]() $\mathbb {F}_p[[G]]$
-modules
$\mathbb {F}_p[[G]]$
-modules
Note that since
![]() $K \not \subseteq M$
, we have that
$K \not \subseteq M$
, we have that
![]() $M \backslash G / K = G/ MK$
is a proper pro-p quotient of
$M \backslash G / K = G/ MK$
is a proper pro-p quotient of
![]() $G/ M \simeq \mathbb {Z}_p$
, hence is finite. Similarly,
$G/ M \simeq \mathbb {Z}_p$
, hence is finite. Similarly,
![]() $M \backslash G / A = G/ MA$
is finite.
$M \backslash G / A = G/ MA$
is finite.
Note that there is an isomorphism of (left)
![]() $\mathbb {F}_p[[M]]$
-modules
$\mathbb {F}_p[[M]]$
-modules
Similarly, there is an isomorphism of (left)
![]() $\mathbb {F}_p[[M]]$
-modules
$\mathbb {F}_p[[M]]$
-modules
The short exact sequence (3.1) gives rise to a long exact sequence in pro-p homology
Note that
Similarly,
Then the long exact sequence could be rewritten as
Since
![]() $M \cap A$
is of type
$M \cap A$
is of type
![]() $FP_m$
, we have that
$FP_m$
, we have that
![]() $H_i(M \cap A, \mathbb {F}_p)$
is finite for
$H_i(M \cap A, \mathbb {F}_p)$
is finite for
![]() $i \leq m$
. Combining with
$i \leq m$
. Combining with
![]() $M \backslash G / A$
is finite, we conclude that
$M \backslash G / A$
is finite, we conclude that
a) Note that M is of type
![]() $FP_m$
if and only if
$FP_m$
if and only if
![]() $H_i(M, \mathbb {F}_p)$
is finite for
$H_i(M, \mathbb {F}_p)$
is finite for
![]() $i \leq m$
. By the above long exact sequence together with the fact that
$i \leq m$
. By the above long exact sequence together with the fact that
![]() $M \backslash G / K$
is finite,
$M \backslash G / K$
is finite,
![]() $H_i(M, \mathbb {F}_p)$
is finite for
$H_i(M, \mathbb {F}_p)$
is finite for
![]() $i \leq m$
if and only if
$i \leq m$
if and only if
![]() $ \oplus _{t \in M \backslash G / K} H_i(M \cap K, \mathbb {F}_p)$
is finite for
$ \oplus _{t \in M \backslash G / K} H_i(M \cap K, \mathbb {F}_p)$
is finite for
![]() $i \leq m-1$
, i.e.,
$i \leq m-1$
, i.e.,
![]() $M \cap K$
is of type
$M \cap K$
is of type
![]() $FP_{m-1}$
.
$FP_{m-1}$
.
b) If M is of type
![]() $FP_{m+1}$
, then
$FP_{m+1}$
, then
![]() $H_{m+1}(M, \mathbb {F}_p)$
is finite and since
$H_{m+1}(M, \mathbb {F}_p)$
is finite and since
![]() $H_m(M \cap A, \mathbb {Z}_p)$
is finite by the long exact sequence
$H_m(M \cap A, \mathbb {Z}_p)$
is finite by the long exact sequence
![]() $H_m(M \cap K, \mathbb {F}_p)$
is finite. We already know by a) that
$H_m(M \cap K, \mathbb {F}_p)$
is finite. We already know by a) that
![]() $M \cap K$
is of type
$M \cap K$
is of type
![]() $FP_{m-1}$
, and hence
$FP_{m-1}$
, and hence
![]() $M \cap K$
is of type
$M \cap K$
is of type
![]() $FP_m$
.
$FP_m$
.
Next, we prove a technical lemma that will be used in the proof of Proposition 3.5. For a pro-p group G with a subset S, denote by
![]() $\langle S \rangle $
the pro-p subgroup of G generated by S.
$\langle S \rangle $
the pro-p subgroup of G generated by S.
Proposition 3.4 Let
![]() $Q = \langle x, y \rangle \simeq \mathbb {Z}_p^2 $
and A be a finitely generated pro-
$Q = \langle x, y \rangle \simeq \mathbb {Z}_p^2 $
and A be a finitely generated pro-
![]() $p \mathbb {Z}_p[[Q]]$
-module. Suppose that for
$p \mathbb {Z}_p[[Q]]$
-module. Suppose that for
![]() $H = \langle x \rangle $
, we have that A is finitely generated as a pro-
$H = \langle x \rangle $
, we have that A is finitely generated as a pro-
![]() $p\ \mathbb {Z}_p[[H]]$
-module. Let
$p\ \mathbb {Z}_p[[H]]$
-module. Let
![]() $H_j = \langle x y^{ - p^j} \rangle $
. Then there is
$H_j = \langle x y^{ - p^j} \rangle $
. Then there is
![]() $j_0> 0$
such that for every
$j_0> 0$
such that for every
![]() $j \geq j_0$
, we have that A is finitely generated as a pro-
$j \geq j_0$
, we have that A is finitely generated as a pro-
![]() $p\ \mathbb {Z}_p[[H_j]]$
-module.
$p\ \mathbb {Z}_p[[H_j]]$
-module.
Proof By Theorem 2.1, if P is a pro-p subgroup of Q, then A is finitely generated as pro-
![]() $p\ \mathbb {Z}_p[[P]]$
-module if and only if
$p\ \mathbb {Z}_p[[P]]$
-module if and only if
![]() $T(Q, P) \cap \Delta (A) = \{1 \}.$
$T(Q, P) \cap \Delta (A) = \{1 \}.$
Let
Since A is finitely generated as a pro-
![]() $p\ \mathbb {Z}_p[[H]]$
-module for every
$p\ \mathbb {Z}_p[[H]]$
-module for every
![]() $\chi \in T(Q, H) \setminus \{ 1 \}$
, we have that
$\chi \in T(Q, H) \setminus \{ 1 \}$
, we have that
![]() $J \not \subseteq \mathrm{Ker} (\overline {\chi })$
. Since
$J \not \subseteq \mathrm{Ker} (\overline {\chi })$
. Since
![]() $\mathbb {Z}_p[[Q]]$
is a Noetherian ring, there is a finite subset
$\mathbb {Z}_p[[Q]]$
is a Noetherian ring, there is a finite subset
![]() $\Lambda $
of J that generates J as an ideal (abstractly or topologically is the same).
$\Lambda $
of J that generates J as an ideal (abstractly or topologically is the same).
We aim to show that for sufficiently big j, we have
![]() $T(Q, H_j) \cap \Delta (A) = \{1 \}.$
Let
$T(Q, H_j) \cap \Delta (A) = \{1 \}.$
Let
![]() $\mu _j \in T(Q, H_j) \setminus \{ 1 \}$
; thus, we aim to show that
$\mu _j \in T(Q, H_j) \setminus \{ 1 \}$
; thus, we aim to show that
![]() $\mu _j \not \in \Delta (A)$
. Then, by Theorem 2.1, A is finitely generated as a pro-
$\mu _j \not \in \Delta (A)$
. Then, by Theorem 2.1, A is finitely generated as a pro-
![]() $p\ \mathbb {Z}_p[[H_j]]$
-module.
$p\ \mathbb {Z}_p[[H_j]]$
-module.
Let
be the continuous ring homomorphism induced by
![]() $\mu _j$
. Since
$\mu _j$
. Since
![]() $\overline {\mu }_j(H_j) = 1$
, we have
$\overline {\mu }_j(H_j) = 1$
, we have
![]() $\mu _j(x) = \mu _j(y^{p^j}) \not = 1.$
Let
$\mu _j(x) = \mu _j(y^{p^j}) \not = 1.$
Let
and
be the continuous ring homomorphism induced by
![]() $\chi $
. Let
$\chi $
. Let
Then, since
![]() $\chi (y) = \mu _j(y)$
,
$\chi (y) = \mu _j(y)$
,
![]() $\chi (x) = 1$
, we have
$\chi (x) = 1$
, we have
![]() $\chi (t_2) = 0$
, and hence
$\chi (t_2) = 0$
, and hence
where
![]() $\lambda = \sum _{i,k \geq 0} z_{i,k} t_1^i t_2^k$
,
$\lambda = \sum _{i,k \geq 0} z_{i,k} t_1^i t_2^k$
,
![]() $z_{i,k} \in \mathbb {Z}_p$
and
$z_{i,k} \in \mathbb {Z}_p$
and
![]() $\lambda |_{t_1 = 0} = \sum _{k \geq 0} z_{0,k} t_2^k$
. Note that
$\lambda |_{t_1 = 0} = \sum _{k \geq 0} z_{0,k} t_2^k$
. Note that
Note that since
![]() $\mathbb {F}$
has characteristic
$\mathbb {F}$
has characteristic
![]() $p> 0$
, we have
$p> 0$
, we have
Consider
 $$ \begin{align*}\lambda |_{t_1 = t_2^{p^j}}: = \sum_{i,k \geq 0} z_{i,k} t_2^{i p^j + k} = \sum_{s \geq 0} \left(\sum_{ i p^j + k = s} z_{i,k}\right) t_2^{s}.\end{align*} $$
$$ \begin{align*}\lambda |_{t_1 = t_2^{p^j}}: = \sum_{i,k \geq 0} z_{i,k} t_2^{i p^j + k} = \sum_{s \geq 0} \left(\sum_{ i p^j + k = s} z_{i,k}\right) t_2^{s}.\end{align*} $$
Then, using that
![]() $\overline {\mu }_j( t_1) = \overline {\mu }_j( t_2^{p^j})$
, we conclude that
$\overline {\mu }_j( t_1) = \overline {\mu }_j( t_2^{p^j})$
, we conclude that
 $$ \begin{align} \overline{\mu}_j(\lambda) &= \overline{\mu}_j(\lambda |_{t_1 = t_2^{p^j}}) = \overline{\mu}_j\left( \sum_{i,k \geq 0} z_{i,k} t_2^{i p^j + k}\right) = \overline{\mu}_j( \sum_{k \geq 0} z_{0,k} t_2^{k}) + \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right)\nonumber \\& = \overline{\mu}_j(\lambda |_{t_1 =0})+ \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right) = \overline{\chi} (\lambda) + \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right). \end{align} $$
$$ \begin{align} \overline{\mu}_j(\lambda) &= \overline{\mu}_j(\lambda |_{t_1 = t_2^{p^j}}) = \overline{\mu}_j\left( \sum_{i,k \geq 0} z_{i,k} t_2^{i p^j + k}\right) = \overline{\mu}_j( \sum_{k \geq 0} z_{0,k} t_2^{k}) + \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right)\nonumber \\& = \overline{\mu}_j(\lambda |_{t_1 =0})+ \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right) = \overline{\chi} (\lambda) + \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right). \end{align} $$
Suppose now that
![]() $\mu _j \in \Delta (A)$
. Then
$\mu _j \in \Delta (A)$
. Then
![]() $\overline {\mu }_j(J) = 0$
, in particular
$\overline {\mu }_j(J) = 0$
, in particular
![]() $\overline {\mu }_j(\Lambda ) = 0.$
On the other hand,
$\overline {\mu }_j(\Lambda ) = 0.$
On the other hand,
![]() $\chi \not \in \Delta (A)$
; hence,
$\chi \not \in \Delta (A)$
; hence,
![]() $\overline {\chi }(J) \not = 0$
. This is equivalent with
$\overline {\chi }(J) \not = 0$
. This is equivalent with
![]() $\overline {\chi }(\Lambda ) \not = 0$
. So there is
$\overline {\chi }(\Lambda ) \not = 0$
. So there is
![]() $\lambda _0 \in \Lambda $
such that
$\lambda _0 \in \Lambda $
such that
Write as before
![]() $\lambda _0 = \sum _{i,k \geq 0} z_{i,k} t_1^i t_2^k$
where
$\lambda _0 = \sum _{i,k \geq 0} z_{i,k} t_1^i t_2^k$
where
![]() $z_{i,k} \in \mathbb {Z}_p$
. Then, by (3.2),
$z_{i,k} \in \mathbb {Z}_p$
. Then, by (3.2),
 $$ \begin{align*}0 = \overline{\mu}_j(\lambda_0) = \overline{\chi} (\lambda_0) + \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right). \end{align*} $$
$$ \begin{align*}0 = \overline{\mu}_j(\lambda_0) = \overline{\chi} (\lambda_0) + \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right). \end{align*} $$
So, for
where
![]() $z_i \in \mathbb {Z}_p$
and using that
$z_i \in \mathbb {Z}_p$
and using that
![]() $ \overline {\chi } (\lambda _0) = \overline {\chi } (\lambda _0 |_{t_1 = 0})$
, we have
$ \overline {\chi } (\lambda _0) = \overline {\chi } (\lambda _0 |_{t_1 = 0})$
, we have
 $$ \begin{align} - \overline{\chi} ( \sum_{i \geq 0} z_i t_2^i) = \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right).\end{align} $$
$$ \begin{align} - \overline{\chi} ( \sum_{i \geq 0} z_i t_2^i) = \overline{\mu}_j\left( \sum_{i \geq 1,k \geq 0} z_{i,k} t_2^{i p^j + k}\right).\end{align} $$
Let
hence,
Then, by (3.3), we conclude that
where for
![]() $z \in \mathbb {Z}_p$
we denote by
$z \in \mathbb {Z}_p$
we denote by
![]() $\overline {z}$
the image of z in
$\overline {z}$
the image of z in
![]() $\mathbb {F}_p = \mathbb {Z}_p/ p \mathbb {Z}_p$
.
$\mathbb {F}_p = \mathbb {Z}_p/ p \mathbb {Z}_p$
.
Consider the map
that sends
![]() $\sum _{i \geq 0} a_i t^i$
to the smallest
$\sum _{i \geq 0} a_i t^i$
to the smallest
![]() $i_0$
such that
$i_0$
such that
![]() $a_{i_0} \not = 0$
, where each
$a_{i_0} \not = 0$
, where each
![]() $a_i \in \mathbb {F}$
. Define
$a_i \in \mathbb {F}$
. Define
Then
 $$ \begin{align} o\left(- \sum_{i \geq 0} \overline{z}_i f_0^i\right) = d k_0. \end{align} $$
$$ \begin{align} o\left(- \sum_{i \geq 0} \overline{z}_i f_0^i\right) = d k_0. \end{align} $$
By (3.4) and (3.5), there is
![]() $\overline {z}_{i,k} \not = 0$
for some
$\overline {z}_{i,k} \not = 0$
for some
![]() $i \geq 1, k \geq 0$
such that
$i \geq 1, k \geq 0$
such that
Note that
![]() $k_0$
depends only on
$k_0$
depends only on
![]() $\lambda _0 \in \Lambda $
, where
$\lambda _0 \in \Lambda $
, where
![]() $\Lambda $
is a finite set, hence it does not depend on j. From the very beginning, we can choose
$\Lambda $
is a finite set, hence it does not depend on j. From the very beginning, we can choose
![]() $j_0 \in \mathbb {Z}_{>0}$
such that
$j_0 \in \mathbb {Z}_{>0}$
such that
Then, for
![]() $j \geq j_0$
, we get a contradiction, so
$j \geq j_0$
, we get a contradiction, so
![]() $\mu _j \not \in \Delta (A)$
as required.
$\mu _j \not \in \Delta (A)$
as required.
Proposition 3.5 Let G be a pro-p group with a normal pro-p subgroup
![]() $G_0$
such that
$G_0$
such that
![]() $G/ G_0 \simeq \mathbb {Z}_p^2$
. Let S be a normal pro-p subgroup of G such that
$G/ G_0 \simeq \mathbb {Z}_p^2$
. Let S be a normal pro-p subgroup of G such that
![]() $G/ S \simeq \mathbb {Z}_p$
,
$G/ S \simeq \mathbb {Z}_p$
,
![]() $G_0 \subseteq S$
, and S is of type
$G_0 \subseteq S$
, and S is of type
![]() $FP_m$
for some
$FP_m$
for some
![]() $m \geq 1$
. Then there is a normal pro-p subgroup
$m \geq 1$
. Then there is a normal pro-p subgroup
![]() $S_0$
of G such that
$S_0$
of G such that
![]() $G/ S_0 \simeq \mathbb {Z}_p$
,
$G/ S_0 \simeq \mathbb {Z}_p$
,
![]() $S \not = S_0$
,
$S \not = S_0$
,
![]() $G_0 \subseteq S_0$
, and
$G_0 \subseteq S_0$
, and
![]() $S_0$
is of type
$S_0$
is of type
![]() $FP_m$
.
$FP_m$
.
Proof Note that since S is a pro-p group of type
![]() $FP_m$
and
$FP_m$
and
![]() $G/ S\simeq \mathbb {Z}_p$
is a pro-p group of type
$G/ S\simeq \mathbb {Z}_p$
is a pro-p group of type
![]() $FP_{\infty }$
, hence of type
$FP_{\infty }$
, hence of type
![]() $FP_m$
, we can conclude that G is a pro-p group of type
$FP_m$
, we can conclude that G is a pro-p group of type
![]() $FP_m$
. Set
$FP_m$
. Set
Since
![]() $Q = G/ G_0$
is a finitely generated abelian pro-p group, hence
$Q = G/ G_0$
is a finitely generated abelian pro-p group, hence
![]() $\mathbb {Z}_p[[Q]]$
is left and right Noetherian and G is of type
$\mathbb {Z}_p[[Q]]$
is left and right Noetherian and G is of type
![]() $FP_m$
, we conclude that
$FP_m$
, we conclude that
Since S is a pro-p group of type
![]() $FP_m$
, we conclude that
$FP_m$
, we conclude that
Then, by Proposition 3.4, for sufficiently big j, we have that
![]() $A_i$
is finitely generated as a pro-
$A_i$
is finitely generated as a pro-
![]() $p\ \mathbb {Z}_p[[H_j]]$
-module, where
$p\ \mathbb {Z}_p[[H_j]]$
-module, where
![]() $H_j = \langle x y^{ - p^j} \rangle \leq Q$
, for every
$H_j = \langle x y^{ - p^j} \rangle \leq Q$
, for every
![]() $ i \leq m$
. Then we define
$ i \leq m$
. Then we define
![]() $S_0$
as the preimage in G of one such
$S_0$
as the preimage in G of one such
![]() $H_j$
.
$H_j$
.
We recall the statement of Theorem 1.1.
Theorem 1.1 Let
![]() $1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups and
$1 \to K \to G \to \Gamma \to 1$
be a short exact sequence of pro-p groups and
![]() $n_0 \geq 1$
be an integer such that:
$n_0 \geq 1$
be an integer such that:
1) G and K are of type
![]() $FP_{n_0}$
,
$FP_{n_0}$
,
2)
![]() $\Gamma ^{ab}$
is infinite,
$\Gamma ^{ab}$
is infinite,
3) there is a normal pro-p subgroup N of K such that
![]() $G'\cap K \subseteq N$
,
$G'\cap K \subseteq N$
,
![]() $K/ N \simeq \mathbb {Z}_p$
and N is of type
$K/ N \simeq \mathbb {Z}_p$
and N is of type
![]() $FP_{n_0-1}$
.
$FP_{n_0-1}$
.
Then there is a normal pro-p subgroup M of G such that
![]() $G/ M \simeq \mathbb {Z}_p$
,
$G/ M \simeq \mathbb {Z}_p$
,
![]() $M \cap K = N$
, and M is of type
$M \cap K = N$
, and M is of type
![]() $FP_{n_0}$
. Furthermore, if K, G, and N are of type
$FP_{n_0}$
. Furthermore, if K, G, and N are of type
![]() $FP_{\infty }$
, then M can be chosen of type
$FP_{\infty }$
, then M can be chosen of type
![]() $FP_{\infty }$
.
$FP_{\infty }$
.
Proof of Theorem 1.1
Consider a commutative diagram

where the lines are short exact sequences of pro-p groups,
![]() $F_n$
is the free pro-p group with a free basis
$F_n$
is the free pro-p group with a free basis
![]() $s_1, \ldots , s_n$
, and the vertical maps are surjective homomorphisms of pro-p groups with the most left map being the identity map.
$s_1, \ldots , s_n$
, and the vertical maps are surjective homomorphisms of pro-p groups with the most left map being the identity map.
Define
where
![]() $\coprod _K$
is the amalgamated free product with amalgam K in the category of pro-p groups, and each
$\coprod _K$
is the amalgamated free product with amalgam K in the category of pro-p groups, and each
Note that since K is normal in
![]() $\Pi $
and
$\Pi $
and
![]() $\Pi / K \simeq \Pi _1/ K \coprod \Pi _2/ K \coprod \cdots \coprod \Pi _n/ K$
is a free pro-p product, we conclude that
$\Pi / K \simeq \Pi _1/ K \coprod \Pi _2/ K \coprod \cdots \coprod \Pi _n/ K$
is a free pro-p product, we conclude that
![]() $\Pi _1 \coprod _K \Pi _2 \coprod _K \cdots \coprod _K \Pi _i$
embeds in
$\Pi _1 \coprod _K \Pi _2 \coprod _K \cdots \coprod _K \Pi _i$
embeds in
![]() $\Pi $
for every
$\Pi $
for every
![]() $1 \leq i \leq n$
.
$1 \leq i \leq n$
.
Recall that
![]() $\Gamma ^{ab}$
is infinite; hence, the image in
$\Gamma ^{ab}$
is infinite; hence, the image in
![]() $\Gamma ^{ab}$
of at least one
$\Gamma ^{ab}$
of at least one
![]() $\pi (s_i)$
has infinite order. Without loss of generality, we can assume that the image of
$\pi (s_i)$
has infinite order. Without loss of generality, we can assume that the image of
![]() $\pi (s_1)$
in
$\pi (s_1)$
in
![]() $\Gamma ^{ab}$
has infinite order. In particular, the restriction map
$\Gamma ^{ab}$
has infinite order. In particular, the restriction map
is an isomorphism.
Note that
![]() $[K, s_1] \subseteq G' \cap K \subseteq N$
, hence
$[K, s_1] \subseteq G' \cap K \subseteq N$
, hence
![]() $\Pi _1'\subseteq N$
. We have
$\Pi _1'\subseteq N$
. We have
![]() $N \subseteq K \subseteq \Pi _1$
where
$N \subseteq K \subseteq \Pi _1$
where
![]() $K/ N \simeq \mathbb {Z}_p, \Pi _1 / K \simeq \mathbb {Z}_p$
, this together with the inclusion
$K/ N \simeq \mathbb {Z}_p, \Pi _1 / K \simeq \mathbb {Z}_p$
, this together with the inclusion
![]() $\Pi _1'\subseteq N$
implies that
$\Pi _1'\subseteq N$
implies that
![]() $\Pi _1 / N \simeq \mathbb {Z}_p^2$
.
$\Pi _1 / N \simeq \mathbb {Z}_p^2$
.
By assumption, K is of type
![]() $FP_{n_0}$
. By Proposition 3.5, there is
$FP_{n_0}$
. By Proposition 3.5, there is
![]() $S_0$
a normal pro-p subgroup of
$S_0$
a normal pro-p subgroup of
![]() $\Pi _1$
such that
$\Pi _1$
such that
Let
be a homomorphism of pro-p groups such that
This is possible since
![]() $\Pi _1 / N \simeq \mathbb {Z}_p^2$
is abelian and
$\Pi _1 / N \simeq \mathbb {Z}_p^2$
is abelian and
![]() $G' \cap K \subseteq N \subseteq S_0$
. Note that
$G' \cap K \subseteq N \subseteq S_0$
. Note that
![]() $K \not \subseteq S_0$
, hence
$K \not \subseteq S_0$
, hence
![]() $\mu (K) \not = 0$
.
$\mu (K) \not = 0$
.
Consider the epimorphism of pro-p groups
Note that
and
Then we view
![]() $\Pi _1 \coprod _K \Pi _2$
as a proper HNN extension
$\Pi _1 \coprod _K \Pi _2$
as a proper HNN extension
with a pro-p base group
![]() $\Pi _1$
, associated pro-p subgroup K and stable letter
$\Pi _1$
, associated pro-p subgroup K and stable letter
![]() $s_2$
. Then, by Lemma 3.3(a),
$s_2$
. Then, by Lemma 3.3(a),
We view
![]() $\Pi _1 \coprod _K \Pi _2 \coprod _K \Pi _3$
as a proper HNN extension with a base pro-p group
$\Pi _1 \coprod _K \Pi _2 \coprod _K \Pi _3$
as a proper HNN extension with a base pro-p group
![]() $\Pi _1 \coprod _K \Pi _2$
, associated pro-p subgroup K and stable letter
$\Pi _1 \coprod _K \Pi _2$
, associated pro-p subgroup K and stable letter
![]() $s_3$
then by Lemma 3.3(a)
$s_3$
then by Lemma 3.3(a)
 $$ \begin{align*}\mathrm{Ker}(\chi) \cap \left( \Pi_1 \coprod_K \Pi_2 \coprod_K \Pi_3\right)\text{ is of type }FP_{n_0}.\end{align*} $$
$$ \begin{align*}\mathrm{Ker}(\chi) \cap \left( \Pi_1 \coprod_K \Pi_2 \coprod_K \Pi_3\right)\text{ is of type }FP_{n_0}.\end{align*} $$
Then, repeating this argument several times, we deduce that
![]() $\mathrm{Ker}(\chi )$
is of type
$\mathrm{Ker}(\chi )$
is of type
![]() $FP_{n_0}$
.
$FP_{n_0}$
.
By construction,
![]() $\mathrm{Ker}(\mu )$
is a quotient of
$\mathrm{Ker}(\mu )$
is a quotient of
![]() $\mathrm{Ker}(\chi )$
. If
$\mathrm{Ker}(\chi )$
. If
![]() $n_0 = 1$
, then
$n_0 = 1$
, then
![]() $\mathrm{Ker}(\chi )$
is finitely generated (as a pro-p group), then any pro-p quotient of
$\mathrm{Ker}(\chi )$
is finitely generated (as a pro-p group), then any pro-p quotient of
![]() $\mathrm{Ker}(\chi )$
is finitely generated (as a pro-p group). In particular,
$\mathrm{Ker}(\chi )$
is finitely generated (as a pro-p group). In particular,
![]() $\mathrm{Ker}(\mu )$
is finitely generated (as a pro-p group).
$\mathrm{Ker}(\mu )$
is finitely generated (as a pro-p group).
Now, for the general case, i.e.,
![]() $n_0 \geq 2$
, we will apply Lemma 3.1. Write
$n_0 \geq 2$
, we will apply Lemma 3.1. Write
![]() $\widetilde {\mathrm{Ker} (\chi )}$
for the image of
$\widetilde {\mathrm{Ker} (\chi )}$
for the image of
![]() $\mathrm{Ker} (\chi )$
in
$\mathrm{Ker} (\chi )$
in
![]() $F_n$
and
$F_n$
and
![]() $\widetilde {\mathrm{Ker}(\mu )}$
for the image of
$\widetilde {\mathrm{Ker}(\mu )}$
for the image of
![]() $\mathrm{Ker}(\mu )$
in
$\mathrm{Ker}(\mu )$
in
![]() $\Gamma $
. By construction,
$\Gamma $
. By construction,
By assumption, N is of type
![]() $FP_{n_0-1}$
and we have already shown that
$FP_{n_0-1}$
and we have already shown that
![]() $\mathrm{Ker}(\chi )$
is of type
$\mathrm{Ker}(\chi )$
is of type
![]() $FP_{n_0}$
. By construction,
$FP_{n_0}$
. By construction,
![]() $\mu (K) \not = 0$
, hence
$\mu (K) \not = 0$
, hence
![]() $K. \mathrm{Ker} (\mu ) \not = \mathrm{Ker}(\mu )$
and since
$K. \mathrm{Ker} (\mu ) \not = \mathrm{Ker}(\mu )$
and since
![]() $G/ \mathrm{Ker}(\mu ) \simeq \mathbb {Z}_p$
, we deduce that
$G/ \mathrm{Ker}(\mu ) \simeq \mathbb {Z}_p$
, we deduce that
![]() $K. \mathrm{Ker}(\mu )$
has finite index in G and so
$K. \mathrm{Ker}(\mu )$
has finite index in G and so
![]() $\widetilde {\mathrm{Ker}(\mu )}$
has finite index in
$\widetilde {\mathrm{Ker}(\mu )}$
has finite index in
![]() $\Gamma $
.
$\Gamma $
.
By Lemma 3.2, since in the short exact sequence of pro-p groups
the pro-p groups G and K are of type
![]() $FP_{n_0}$
(it suffices that K is of type
$FP_{n_0}$
(it suffices that K is of type
![]() $FP_{n_0-1}$
), we deduce that
$FP_{n_0-1}$
), we deduce that
![]() $\Gamma $
is of type
$\Gamma $
is of type
![]() $FP_{n_0}$
. Then
$FP_{n_0}$
. Then
![]() $\widetilde {\mathrm{Ker}(\mu )}$
is a pro-p group of type
$\widetilde {\mathrm{Ker}(\mu )}$
is a pro-p group of type
![]() $FP_{n_0}$
. Then we can apply Lemma 3.1 for the commutative diagram
$FP_{n_0}$
. Then we can apply Lemma 3.1 for the commutative diagram

to deduce that
![]() $\mathrm{Ker}(\mu )$
is a pro-p group of type
$\mathrm{Ker}(\mu )$
is a pro-p group of type
![]() $FP_{n_0}$
. Finally, we set
$FP_{n_0}$
. Finally, we set
![]() $M = \mathrm{Ker}(\mu )$
.
$M = \mathrm{Ker}(\mu )$
.
Proof of Corollary 1.2
We define M as in the proof of Theorem 1.1 for
![]() $\Gamma = F_n$
and
$\Gamma = F_n$
and
![]() $\pi $
the identity map,
$\pi $
the identity map,
![]() $\mu = \chi $
. Thus,
$\mu = \chi $
. Thus,
![]() $M = \mathrm{Ker}(\chi ) = \mathrm{Ker}(\mu )$
is a normal pro-p subgroup of G,
$M = \mathrm{Ker}(\chi ) = \mathrm{Ker}(\mu )$
is a normal pro-p subgroup of G,
![]() $G/ M \simeq \mathbb {Z}_p$
and M is of type
$G/ M \simeq \mathbb {Z}_p$
and M is of type
![]() $FP_{n_0}$
. We view
$FP_{n_0}$
. We view
as a proper HNN extension with a base pro-p subgroup
associated pro-p subgroup K and stable letter
![]() $s_n$
. By the proof of Theorem 1.1,
$s_n$
. By the proof of Theorem 1.1,
Suppose that M is of type
![]() $FP_{n_0+1}$
. By Lemma 3.3(b),
$FP_{n_0+1}$
. By Lemma 3.3(b),
![]() $N = M \cap K$
is of type
$N = M \cap K$
is of type
![]() $FP_{n_0}$
, a contradiction. Hence, M is not of type
$FP_{n_0}$
, a contradiction. Hence, M is not of type
![]() $FP_{n_0 + 1}$
. This completes the proof of the corollary.
$FP_{n_0 + 1}$
. This completes the proof of the corollary.
Theorem 3.6 Let
![]() $G = K \rtimes \Gamma $
be a pro-p group such that:
$G = K \rtimes \Gamma $
be a pro-p group such that:
1) K is a finitely generated pro-p group, i.e., is of type
![]() $FP_1$
,
$FP_1$
,
2) there is a normal pro-p subgroup N of K with
![]() $K/ N \simeq \mathbb {Z}_p$
and N is not finitely generated,
$K/ N \simeq \mathbb {Z}_p$
and N is not finitely generated,
3)
![]() $\Gamma $
a finitely generated free pro-p group with
$\Gamma $
a finitely generated free pro-p group with
![]() $d(\Gamma ) \geq 2$
.
$d(\Gamma ) \geq 2$
.
Then G is incoherent (in the category of pro-p groups).
Proof We claim that there is a finitely generated non-procyclic pro-p subgroup
![]() $\Gamma _0$
of
$\Gamma _0$
of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma _0$
acts trivially on the abilianization
$\Gamma _0$
acts trivially on the abilianization
![]() $K^{ab} = K/ K'$
via conjugation. Indeed, let
$K^{ab} = K/ K'$
via conjugation. Indeed, let
![]() $T = \mathrm{tor}(K/ K')$
be the torsion pro-p subgroup of
$T = \mathrm{tor}(K/ K')$
be the torsion pro-p subgroup of
![]() $K^{ab}$
. Then
$K^{ab}$
. Then
![]() $V = K^{ab}/ T \simeq \mathbb {Z}_p^d$
, where
$V = K^{ab}/ T \simeq \mathbb {Z}_p^d$
, where
![]() $d \geq 1$
. Note that the conjugation action of
$d \geq 1$
. Note that the conjugation action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $V \simeq \mathbb {Z}_p^d$
induces a homomorphism
$V \simeq \mathbb {Z}_p^d$
induces a homomorphism
Note that
![]() $\mathrm{Im} (\rho )$
is a pro-p subgroup of
$\mathrm{Im} (\rho )$
is a pro-p subgroup of
![]() $GL_d(\mathbb {Z}_p)$
, hence is p-adic analytic and there is an upper bound on the number of generators of any finitely generated pro-p subgroup of
$GL_d(\mathbb {Z}_p)$
, hence is p-adic analytic and there is an upper bound on the number of generators of any finitely generated pro-p subgroup of
![]() $\mathrm{Im} (\rho )$
[Reference Dixon, Du Sautoy, Mann and Segal7]. Hence,
$\mathrm{Im} (\rho )$
[Reference Dixon, Du Sautoy, Mann and Segal7]. Hence,
![]() $\rho $
is not injective. Alternatively, we can use the main result of [Reference Barnea and Larsen1] to deduce that
$\rho $
is not injective. Alternatively, we can use the main result of [Reference Barnea and Larsen1] to deduce that
![]() $\rho $
is not injective. Thus,
$\rho $
is not injective. Thus,
![]() $\mathrm{Ker}(\rho )$
is a nontrivial normal pro-p subgroup of
$\mathrm{Ker}(\rho )$
is a nontrivial normal pro-p subgroup of
![]() $\Gamma $
and we can choose
$\Gamma $
and we can choose
![]() $\Gamma _0$
any non-procyclic finitely generated pro-p subgroup of
$\Gamma _0$
any non-procyclic finitely generated pro-p subgroup of
![]() $\mathrm{Ker}(\rho )$
.
$\mathrm{Ker}(\rho )$
.
Set
![]() $G_0 = K \rtimes \Gamma _0$
. Then, by Corollary 1.2, there is a normal pro-p subgroup M of
$G_0 = K \rtimes \Gamma _0$
. Then, by Corollary 1.2, there is a normal pro-p subgroup M of
![]() $G_0$
such that
$G_0$
such that
![]() $G_0/ M \simeq \mathbb {Z}_p$
,
$G_0/ M \simeq \mathbb {Z}_p$
,
![]() $M \cap K = N$
, and M is
$M \cap K = N$
, and M is
![]() $FP_1$
but not
$FP_1$
but not
![]() $FP_2$
, i.e., it is finitely generated as a pro-p group, but is not finitely presented as a pro-p group. Thus,
$FP_2$
, i.e., it is finitely generated as a pro-p group, but is not finitely presented as a pro-p group. Thus,
![]() $G_0$
and hence G are incoherent (in the category of pro-p groups). This completes the proof.
$G_0$
and hence G are incoherent (in the category of pro-p groups). This completes the proof.
Proof of Corollary 1.3
Let
![]() $\Gamma _0$
be a finitely generated, free non-abelian pro-p subgroup of
$\Gamma _0$
be a finitely generated, free non-abelian pro-p subgroup of
![]() $\Gamma $
. Consider the preimage
$\Gamma $
. Consider the preimage
![]() $G_0$
of
$G_0$
of
![]() $\Gamma _0$
in G, i.e., there is a short exact sequence
$\Gamma _0$
in G, i.e., there is a short exact sequence
Note that
![]() $G_0 = K \rtimes \Gamma _0$
, then by Theorem 3.6,
$G_0 = K \rtimes \Gamma _0$
, then by Theorem 3.6,
![]() $G_0$
is not coherent.
$G_0$
is not coherent.
4 More results on coherence
In this section, we show some applications of Corollary 1.3.
We recall the definition of the class of pro-p groups
![]() $\mathcal {L}$
. It uses the extension of centralizer construction. We define inductively the class
$\mathcal {L}$
. It uses the extension of centralizer construction. We define inductively the class
![]() $\mathcal {G}_n$
of pro-p groups by setting
$\mathcal {G}_n$
of pro-p groups by setting
![]() $\mathcal {G}_0$
as the class of all finitely generated free pro-p groups and a group
$\mathcal {G}_0$
as the class of all finitely generated free pro-p groups and a group
![]() $G_{n} \in \mathcal {G}_n$
if there is a decomposition
$G_{n} \in \mathcal {G}_n$
if there is a decomposition
where
![]() $G_{n-1} \in \mathcal {G}_{n-1}$
, C is self-centralized procyclic subgroup of
$G_{n-1} \in \mathcal {G}_{n-1}$
, C is self-centralized procyclic subgroup of
![]() $G_{n-1}$
, and A is a finitely generated free abelian pro-p group such that C is a direct summand of A. The class
$G_{n-1}$
, and A is a finitely generated free abelian pro-p group such that C is a direct summand of A. The class
![]() $\mathcal {L}$
is defined as the class of all finitely generated pro-p subgroups G of
$\mathcal {L}$
is defined as the class of all finitely generated pro-p subgroups G of
![]() $G_n$
, where
$G_n$
, where
![]() $G_n$
runs through all pro-p groups in
$G_n$
runs through all pro-p groups in
![]() $ {\mathcal G}_n$
for
$ {\mathcal G}_n$
for
![]() $n \geq 0$
. The minimal n such that
$n \geq 0$
. The minimal n such that
![]() $G \leq G_n \in {\mathcal {G}_n}$
is called the weight of G.
$G \leq G_n \in {\mathcal {G}_n}$
is called the weight of G.
Proposition 4.1 [Reference Kochloukova and Zalesskii14]
Let
![]() $K \in {\mathcal L}$
be a nontrivial pro-p group. Then
$K \in {\mathcal L}$
be a nontrivial pro-p group. Then
![]() $K^{ab} = K/ K'$
is infinite.
$K^{ab} = K/ K'$
is infinite.
Proof of Corollary 1.4
By Proposition 4.1,
![]() $K^{ab}$
is infinite. Let N be a normal pro-p subgroup of K such that
$K^{ab}$
is infinite. Let N be a normal pro-p subgroup of K such that
![]() $K/ N \simeq \mathbb {Z}_p$
. By part (4) from the main theorem of [Reference Kochloukova and Zalesskii14], we have that N is not finitely generated as a pro-p group. Then we can apply Corollary 1.3. This completes the proof.
$K/ N \simeq \mathbb {Z}_p$
. By part (4) from the main theorem of [Reference Kochloukova and Zalesskii14], we have that N is not finitely generated as a pro-p group. Then we can apply Corollary 1.3. This completes the proof.
Definition Given a finite simplicial graph X, the pro-p RAAG associated with X is the pro-p group defined by the presentation in the category of pro-p groups
where
![]() $V(X)$
is the set of vertices of X.
$V(X)$
is the set of vertices of X.
Lemma 4.2 Let G be a Demushkin pro-p group such that
![]() $d(G) = 2$
. Then G is soluble and has Euler characteristic 0.
$d(G) = 2$
. Then G is soluble and has Euler characteristic 0.
Proof The classification of Demushkin groups has several cases described in Theorems 2.3–2.5. In the case of 2-generated Demushkin group, we have a 1-relation presentation with a relation of the type
![]() $[x_1, x_2]$
or
$[x_1, x_2]$
or
![]() $x_1^q[ x_1, x_2]$
, where q is a power of p or of the type
$x_1^q[ x_1, x_2]$
, where q is a power of p or of the type
![]() $2^f + 2$
,
$2^f + 2$
,
![]() $p = 2$
. In all these cases, the group is soluble, since it is
$p = 2$
. In all these cases, the group is soluble, since it is
![]() $\langle x_1 \rangle \rtimes \langle x_2 \rangle $
and has zero Euler characteristic.
$\langle x_1 \rangle \rtimes \langle x_2 \rangle $
and has zero Euler characteristic.
Proof of Corollary 1.5
We claim that
![]() $\Gamma $
has a free non-abelian pro-p subgroup F. Suppose first that
$\Gamma $
has a free non-abelian pro-p subgroup F. Suppose first that
![]() $\Gamma $
is a pro-p RAAG. Let
$\Gamma $
is a pro-p RAAG. Let
![]() $v_1,v_2$
be vertices of the graph that defines the pro-p RAAG
$v_1,v_2$
be vertices of the graph that defines the pro-p RAAG
![]() $\Gamma $
that are not adjacent. Then the pro-p subgroup F of
$\Gamma $
that are not adjacent. Then the pro-p subgroup F of
![]() $\Gamma $
generated by
$\Gamma $
generated by
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, is a retract of
$v_2$
, is a retract of
![]() $\Gamma $
, hence it is non-abelian free pro-p.
$\Gamma $
, hence it is non-abelian free pro-p.
If
![]() $\Gamma $
is a non-soluble Demushkin group, then every pro-p subgroup of infinite index in
$\Gamma $
is a non-soluble Demushkin group, then every pro-p subgroup of infinite index in
![]() $\Gamma $
has cohomological dimension 1, so is free pro-p [Reference Serre24, Ex. 5b), p. 44]. Furthermore, the abelianization of
$\Gamma $
has cohomological dimension 1, so is free pro-p [Reference Serre24, Ex. 5b), p. 44]. Furthermore, the abelianization of
![]() $\Gamma $
is infinite, so we can set
$\Gamma $
is infinite, so we can set
![]() $F $
to be a normal pro-p subgroup of
$F $
to be a normal pro-p subgroup of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma / F \simeq \mathbb {Z}_p$
.
$\Gamma / F \simeq \mathbb {Z}_p$
.
We claim that there is a normal pro-p subgroup N of K such that N is not finitely generated (as a pro-p group) and
![]() $K/ N \simeq \mathbb {Z}_p$
. Suppose first that K is a non-abelian pro-p RAAG. Let
$K/ N \simeq \mathbb {Z}_p$
. Suppose first that K is a non-abelian pro-p RAAG. Let
![]() $w_1$
and
$w_1$
and
![]() $w_2$
be vertices of the graph that defines the pro-p RAAG K that are not adjacent. Then the pro-p subgroup
$w_2$
be vertices of the graph that defines the pro-p RAAG K that are not adjacent. Then the pro-p subgroup
![]() $F_0$
of K generated by
$F_0$
of K generated by
![]() $w_1$
and
$w_1$
and
![]() $w_2$
is non-abelian free pro-p and it is a retract of K. Note that any normal pro-p subgroup S of
$w_2$
is non-abelian free pro-p and it is a retract of K. Note that any normal pro-p subgroup S of
![]() $F_0$
such that
$F_0$
such that
![]() $F_0/ S \simeq \mathbb {Z}_p$
is not finitely generated (as a pro-p group), hence any preimage N of S in K is not finitely generated (as a pro-p group).
$F_0/ S \simeq \mathbb {Z}_p$
is not finitely generated (as a pro-p group), hence any preimage N of S in K is not finitely generated (as a pro-p group).
Suppose that K is a non-soluble Demushkin group. Note that
![]() $K/ K'$
is infinite and let N be a normal pro-p subgroup of K such that
$K/ K'$
is infinite and let N be a normal pro-p subgroup of K such that
![]() $K/ N \simeq \mathbb {Z}_p$
. If N is finitely generated (as a pro-p subgroup), together with the fact that N is free pro-p, we conclude that N has finite Euler characteristic
$K/ N \simeq \mathbb {Z}_p$
. If N is finitely generated (as a pro-p subgroup), together with the fact that N is free pro-p, we conclude that N has finite Euler characteristic
![]() $\chi (N)$
,
$\chi (N)$
,
![]() $\chi (K/N) = \chi (\mathbb {Z}_p) = 0$
and
$\chi (K/N) = \chi (\mathbb {Z}_p) = 0$
and
so
![]() $d(K) = 2$
. But by Lemma 4.2 2-generated Demushkin groups are soluble, a contradiction.
$d(K) = 2$
. But by Lemma 4.2 2-generated Demushkin groups are soluble, a contradiction.
Finally, by Corollary 1.3, G is not coherent.
Proposition 4.3 Let
![]() $ 1 \to K \to G \to \mathbb {Z}_p^m \to 1$
be a short exact sequence of pro-p groups with K free pro-p or Demushkin pro-p group. Then G is coherent (as a pro-p group).
$ 1 \to K \to G \to \mathbb {Z}_p^m \to 1$
be a short exact sequence of pro-p groups with K free pro-p or Demushkin pro-p group. Then G is coherent (as a pro-p group).
Proof Let H be a finitely generated, pro-p subgroup of G. We aim to prove that H is
![]() $FP_{\infty }$
, in particular is finitely presented.
$FP_{\infty }$
, in particular is finitely presented.
Consider the short exact sequence of pro-p groups
where Q is a pro-p subgroup of
![]() $\mathbb {Z}_p^m$
, so is finitely generated, abelian, and
$\mathbb {Z}_p^m$
, so is finitely generated, abelian, and
![]() $K_0 = K \cap H$
. Recall that an infinite index subgroup in a Demushkin group is free pro-p, in particular
$K_0 = K \cap H$
. Recall that an infinite index subgroup in a Demushkin group is free pro-p, in particular
![]() $K_0$
is either free pro-p or Demushkin. In the latter,
$K_0$
is either free pro-p or Demushkin. In the latter,
![]() $K_0$
is
$K_0$
is
![]() $FP_{\infty }$
, hence H is
$FP_{\infty }$
, hence H is
![]() $FP_{\infty }$
. Thus, we can assume from now on that
$FP_{\infty }$
. Thus, we can assume from now on that
![]() $K_0$
is free pro-p.
$K_0$
is free pro-p.
Consider the LHS spectral sequence
Note that
![]() $E_{i,j}^2 = 0$
for
$E_{i,j}^2 = 0$
for
![]() $j \geq 2$
and
$j \geq 2$
and
Thus,
![]() $E_{i,j}^3 = E_{i,j}^{\infty }$
and
$E_{i,j}^3 = E_{i,j}^{\infty }$
and
since
![]() $E_{i,0}^2$
is finite for all i. Note that
$E_{i,0}^2$
is finite for all i. Note that
since
![]() $E_{i+2,0}^2$
is finite for all i.
$E_{i+2,0}^2$
is finite for all i.
Since H is finitely generated and by the convergence of the spectral sequence, we have that
hence
Since
![]() $\mathbb {F}_p[[Q]]$
is a local ring, this implies that
$\mathbb {F}_p[[Q]]$
is a local ring, this implies that
![]() $H_1(K_0, \mathbb {F}_p)$
is finitely generated as a pro-
$H_1(K_0, \mathbb {F}_p)$
is finitely generated as a pro-
![]() $p\ \mathbb {F}_p[[Q]]$
-module. Then
$p\ \mathbb {F}_p[[Q]]$
-module. Then
![]() $E_{j,1}^2$
is finite for
$E_{j,1}^2$
is finite for
![]() $j \geq 0$
.
$j \geq 0$
.
By the convergence of the spectral sequence, there is an exact sequence for
![]() $i \geq 2$
$i \geq 2$
with both
![]() $ E_{i-1,1}^{\infty } $
and
$ E_{i-1,1}^{\infty } $
and
![]() $ E_{i,0}^{\infty }$
finite. Hence,
$ E_{i,0}^{\infty }$
finite. Hence,
![]() $ H_i(H, \mathbb {F}_p) $
is finite for
$ H_i(H, \mathbb {F}_p) $
is finite for
![]() $i \geq 2$
and H is of type
$i \geq 2$
and H is of type
![]() $FP_{\infty }$
, in particular is finitely presented as a pro-p group.
$FP_{\infty }$
, in particular is finitely presented as a pro-p group.
5 Proofs of Corollaries 1.6 and 1.7
Proof of Corollary 1.6
Let F be a finitely generated free non-procyclic pro-p group that embeds as a closed subgroup of
![]() $\mathrm{Out}(K)$
. Note that
$\mathrm{Out}(K)$
. Note that
![]() $G = K \rtimes F$
is a pro-p group that embeds as a closed subgroup of
$G = K \rtimes F$
is a pro-p group that embeds as a closed subgroup of
![]() $\mathrm{Aut}(K)$
and by Theorem 3.6 G is incoherent (in the category of pro-p groups). Finally,
$\mathrm{Aut}(K)$
and by Theorem 3.6 G is incoherent (in the category of pro-p groups). Finally,
![]() $G_0 = G \cap \mathrm{Aut}_0(G)$
is a pro-p subgroup of finite index in G, hence
$G_0 = G \cap \mathrm{Aut}_0(G)$
is a pro-p subgroup of finite index in G, hence
![]() $G_0$
is incoherent (in the category of pro-p groups).
$G_0$
is incoherent (in the category of pro-p groups).
Proof of Corollary 1.7
We recall first some results from [Reference Lubotzky18]. Let G be a finitely generated pro-p group and
![]() $\mathrm{Aut}(G)$
denote all continuous automorphisms of G (which coincide with the abstract automorphisms of G). Denote
$\mathrm{Aut}(G)$
denote all continuous automorphisms of G (which coincide with the abstract automorphisms of G). Denote
![]() $\mathrm{Inn}(G)$
the group of the internal automorphisms. The group
$\mathrm{Inn}(G)$
the group of the internal automorphisms. The group
![]() $\mathrm{Aut}(G)$
is a profinite group.
$\mathrm{Aut}(G)$
is a profinite group.
Lemma 5.1 [Reference Lubotzky18]
a) Let G be a finitely generated pro-p group and
![]() $G^*$
be the Frattini subgroup of G, i.e., the intersection of all maximal open subgroups of G. Then
$G^*$
be the Frattini subgroup of G, i.e., the intersection of all maximal open subgroups of G. Then
![]() $\mathrm{Ker}(\mathrm{Aut}(G) \to \mathrm{Aut}(G/ G^*))$
is a pro-p subgroup of
$\mathrm{Ker}(\mathrm{Aut}(G) \to \mathrm{Aut}(G/ G^*))$
is a pro-p subgroup of
![]() $\mathrm{Aut}(G)$
of finite index.
$\mathrm{Aut}(G)$
of finite index.
b) Let F be a finitely generated free pro-p group and N be a characteristic pro-p subgroup of F. Then the map
![]() $\mathrm{Aut}(F) \to \mathrm{Aut}(F/N)$
, obtained by taking the induced automorphisms, is surjective.
$\mathrm{Aut}(F) \to \mathrm{Aut}(F/N)$
, obtained by taking the induced automorphisms, is surjective.
We set
![]() $\mathrm{Aut}_0(G) = \mathrm{Ker}(\mathrm{Aut}(G) \to \mathrm{Aut}(G/ G^*))$
and
$\mathrm{Aut}_0(G) = \mathrm{Ker}(\mathrm{Aut}(G) \to \mathrm{Aut}(G/ G^*))$
and
![]() $\mathrm{Out}_0(G) =\mathrm{Aut}_0(G)/ \mathrm{Inn}(G)$
.
$\mathrm{Out}_0(G) =\mathrm{Aut}_0(G)/ \mathrm{Inn}(G)$
.
Lemma 5.2 Suppose K is a finitely generated, free pro-p group,
![]() $d(K) = n \geq 2$
, and
$d(K) = n \geq 2$
, and
![]() $M $
is the maximal pro-p metabelian quotient of K. Then
$M $
is the maximal pro-p metabelian quotient of K. Then
![]() $\mathrm{Out}(M)$
contains a finitely generated pro-p subgroup H such that H has a metabelian pro-p quotient that is not finitely presented (as a pro-p group).
$\mathrm{Out}(M)$
contains a finitely generated pro-p subgroup H such that H has a metabelian pro-p quotient that is not finitely presented (as a pro-p group).
Lemma 5.2 implies Corollary 1.7: If
![]() $\mathrm{Out}(K)$
contains a pro-p free non-procyclic subgroup, we can apply Corollary 1.6. Then we can assume that
$\mathrm{Out}(K)$
contains a pro-p free non-procyclic subgroup, we can apply Corollary 1.6. Then we can assume that
![]() $\mathrm{Out}(K)$
does not contain a pro-p free non-procyclic subgroup. We can further assume that the pro-p version of the Bieri–Strebel result holds; otherwise, Corollary 1.7 holds, i.e., if a finitely presented pro-p group does not contain a free non-procyclic pro-p subgroup, then any metabelian pro-p quotient of that group is a finitely presented pro-p group.
$\mathrm{Out}(K)$
does not contain a pro-p free non-procyclic subgroup. We can further assume that the pro-p version of the Bieri–Strebel result holds; otherwise, Corollary 1.7 holds, i.e., if a finitely presented pro-p group does not contain a free non-procyclic pro-p subgroup, then any metabelian pro-p quotient of that group is a finitely presented pro-p group.
Let H be a pro-p subgroup of
![]() $\mathrm{Out}(M)$
as in Lemma 5.2. Since
$\mathrm{Out}(M)$
as in Lemma 5.2. Since
![]() $\mathrm{Aut}_0(M)$
has finite index in
$\mathrm{Aut}_0(M)$
has finite index in
![]() $\mathrm{Aut}(M)$
, without loss of generality, we can assume that
$\mathrm{Aut}(M)$
, without loss of generality, we can assume that
![]() $H \subseteq \mathrm{Out}_0(M) $
. The epimorphism of pro-p groups
$H \subseteq \mathrm{Out}_0(M) $
. The epimorphism of pro-p groups
![]() $\mathrm{Aut}_0(K) \to \mathrm{Aut}_0(M)$
induces an epimorphism of pro-p groups
$\mathrm{Aut}_0(K) \to \mathrm{Aut}_0(M)$
induces an epimorphism of pro-p groups
![]() $\mathrm{Out}_0(K) \to \mathrm{Out}_0(M)$
. Then there is a finitely generated pro-p subgroup
$\mathrm{Out}_0(K) \to \mathrm{Out}_0(M)$
. Then there is a finitely generated pro-p subgroup
![]() $\widetilde {H}$
of
$\widetilde {H}$
of
![]() $\mathrm{Out}_0(K)$
that maps surjectively to H, in particular
$\mathrm{Out}_0(K)$
that maps surjectively to H, in particular
![]() $\widetilde {H}$
has a metabelian pro-p quotient that is not finitely presented (as a pro-p group). Then, by the previous considerations,
$\widetilde {H}$
has a metabelian pro-p quotient that is not finitely presented (as a pro-p group). Then, by the previous considerations,
![]() $\widetilde {H}$
is not a finitely presented pro-p group.
$\widetilde {H}$
is not a finitely presented pro-p group.
Note that
![]() $\mathrm{Inn}(K) \simeq K$
. Consider the short exact sequence
$\mathrm{Inn}(K) \simeq K$
. Consider the short exact sequence
and let
![]() $H_0$
be the preimage of
$H_0$
be the preimage of
![]() $\widetilde {H}$
in
$\widetilde {H}$
in
![]() $\mathrm{Aut}_0(K)$
. Then there is a short exact sequence
$\mathrm{Aut}_0(K)$
. Then there is a short exact sequence
of pro-p groups. Since K is a finitely generated pro-p group, we have that
![]() $H_0$
is a finitely generated pro-p group and
$H_0$
is a finitely generated pro-p group and
![]() $H_0$
is not finitely presented; otherwise,
$H_0$
is not finitely presented; otherwise,
![]() $\widetilde {H}$
would be a finitely presented pro-p group, a contradiction. Thus,
$\widetilde {H}$
would be a finitely presented pro-p group, a contradiction. Thus,
![]() $\mathrm{Aut}_0(K)$
is incoherent (in the category of pro-p groups).
$\mathrm{Aut}_0(K)$
is incoherent (in the category of pro-p groups).
Proof of Lemma 5.2
Here, we use significantly ideas introduced in [Reference Romankov21]. We fix
![]() $x_1, x_2, \ldots , x_n$
a generating set of M. Define
$x_1, x_2, \ldots , x_n$
a generating set of M. Define
where
![]() $\mathrm{Aut}(M)$
denotes continuous automorphisms of M. In fact, every abstract automorphism of a finitely generated pro-p group is a continuous one. Then there is a short exact sequence of profinite groups
$\mathrm{Aut}(M)$
denotes continuous automorphisms of M. In fact, every abstract automorphism of a finitely generated pro-p group is a continuous one. Then there is a short exact sequence of profinite groups
By [Reference Romankov21], there is a Bachmut embedding
![]() $\beta $
of
$\beta $
of
![]() $\mathrm{IAut}(M)$
in
$\mathrm{IAut}(M)$
in
![]() $GL_n(\mathbb {Z}_p[[M^{ab}]])$
, where
$GL_n(\mathbb {Z}_p[[M^{ab}]])$
, where
![]() $M^{ab}$
is the maximal abelian pro-p quotient of M. By [Reference Romankov21], where
$M^{ab}$
is the maximal abelian pro-p quotient of M. By [Reference Romankov21], where
![]() $\mathrm{Aut}(M)$
acts on the right,
$\mathrm{Aut}(M)$
acts on the right,
 $$ \begin{align*}\beta(\varphi) = \left( \frac{\partial }{\partial x_j} (x_i^{ \varphi})\right) \text{ and } \frac{\partial}{\partial x_j} : M \to \mathbb{Z}_p[[M^{ab}]] \text{ are the Fox derivatives defined by }\end{align*} $$
$$ \begin{align*}\beta(\varphi) = \left( \frac{\partial }{\partial x_j} (x_i^{ \varphi})\right) \text{ and } \frac{\partial}{\partial x_j} : M \to \mathbb{Z}_p[[M^{ab}]] \text{ are the Fox derivatives defined by }\end{align*} $$
 $$ \begin{align*}\frac{\partial}{\partial x_j} (1) = 0, \ \frac{\partial}{\partial x_j} ( g_1 g_2) = \frac{\partial}{ \partial x_j} ( g_1) + \overline{g}_1 \frac{\partial}{\partial x_j} (g_2), \ \frac{\partial}{ \partial x_j} (x_i) = \delta_{i,j},\end{align*} $$
$$ \begin{align*}\frac{\partial}{\partial x_j} (1) = 0, \ \frac{\partial}{\partial x_j} ( g_1 g_2) = \frac{\partial}{ \partial x_j} ( g_1) + \overline{g}_1 \frac{\partial}{\partial x_j} (g_2), \ \frac{\partial}{ \partial x_j} (x_i) = \delta_{i,j},\end{align*} $$
where
![]() $\overline {g}_1$
is the image of
$\overline {g}_1$
is the image of
![]() $g_1 \in M$
in
$g_1 \in M$
in
![]() $ M^{ ab}$
,
$ M^{ ab}$
,
![]() $\delta _{i,j}$
is the Kronecker symbol.
$\delta _{i,j}$
is the Kronecker symbol.
Set
![]() $s_i$
for the image of
$s_i$
for the image of
![]() $x_i-1$
in
$x_i-1$
in
![]() $\mathbb {Z}_p[[M^{ ab}]]$
; thus,
$\mathbb {Z}_p[[M^{ ab}]]$
; thus,
Define
By [Reference Romankov21],
is a multiplicative abelian group, where
![]() $\Delta $
is the unique maximal ideal of
$\Delta $
is the unique maximal ideal of
![]() $\mathbb {Z}_p[[M^{ab}]]$
, and the
$\mathbb {Z}_p[[M^{ab}]]$
, and the
![]() $GL_n(\mathbb {Z}_p)$
-action via conjugation on the abelianization of
$GL_n(\mathbb {Z}_p)$
-action via conjugation on the abelianization of
![]() $\mathrm{IAut}(M)$
induces an action on
$\mathrm{IAut}(M)$
induces an action on
![]() $\mathrm{det}(\mathrm{IAut}(M)) = P$
. Then we have a short exact sequence of profinite groups
$\mathrm{det}(\mathrm{IAut}(M)) = P$
. Then we have a short exact sequence of profinite groups
Consider the pro-p group
Let Q be the maximal pro-p quotient of P that has exponent p. Then there is a pro-p subgroup T of
![]() $ \mathrm{Aut}(M)/ \mathrm{Ker} (\mathrm{det}) $
and a short exact sequence of pro-p groups
$ \mathrm{Aut}(M)/ \mathrm{Ker} (\mathrm{det}) $
and a short exact sequence of pro-p groups
and a pro-p quotient
![]() $T_0$
of T together with a short exact sequence of pro-p groups
$T_0$
of T together with a short exact sequence of pro-p groups
By [Reference Romankov22, (7)],
and for
![]() $\delta \in \Delta $
using
$\delta \in \Delta $
using
![]() $[\delta ]$
for the image of
$[\delta ]$
for the image of
![]() $ 1 + p \delta $
in Q, we have that
$ 1 + p \delta $
in Q, we have that
Thus, the multiplicative subgroup of Q generated by
![]() $\{ [\delta ] \ | \ \delta \in \Delta \}$
could be identified with the additive group
$\{ [\delta ] \ | \ \delta \in \Delta \}$
could be identified with the additive group
![]() $\Delta / p \Delta $
. Furthermore, using the long exact sequence in homology for the short exact sequence
$\Delta / p \Delta $
. Furthermore, using the long exact sequence in homology for the short exact sequence
we have a long exact sequence
Note that
![]() $\mathrm{Tor}_1^{\mathbb {Z}_p}(\mathbb {F}_p, \mathbb {F}_p) \simeq \mathbb {F}_p$
and thus we have a short exact sequence of additive pro-p groups
$\mathrm{Tor}_1^{\mathbb {Z}_p}(\mathbb {F}_p, \mathbb {F}_p) \simeq \mathbb {F}_p$
and thus we have a short exact sequence of additive pro-p groups
where
![]() $\Omega $
is the augmentation ideal of
$\Omega $
is the augmentation ideal of
![]() $ \mathbb {F}_p[[s_1, s_2, \ldots , s_n]] $
and for the canonical projection
$ \mathbb {F}_p[[s_1, s_2, \ldots , s_n]] $
and for the canonical projection
the composition map
![]() $\nu \circ \pi : \Delta \to \Omega $
is the restriction of the map
$\nu \circ \pi : \Delta \to \Omega $
is the restriction of the map
![]() $\mathbb {Z}_p[[s_1, s_2, \ldots , s_n]] \to \mathbb {F}_p[[s_1, s_2, \ldots , s_n]]$
that reduces coefficients mod p. Actually,
$\mathbb {Z}_p[[s_1, s_2, \ldots , s_n]] \to \mathbb {F}_p[[s_1, s_2, \ldots , s_n]]$
that reduces coefficients mod p. Actually,
![]() $\mathrm{Ker}(\nu ) = \mathbb {F}_p$
is generated as an additive group by
$\mathrm{Ker}(\nu ) = \mathbb {F}_p$
is generated as an additive group by
![]() $p + p \Delta $
.
$p + p \Delta $
.
Consider now
![]() $\varphi _2 \in \mathrm{Aut}(M)$
given by
$\varphi _2 \in \mathrm{Aut}(M)$
given by
and
![]() $\varphi _1 \in \mathrm{IAut}(M)$
such that
$\varphi _1 \in \mathrm{IAut}(M)$
such that
Note that
![]() $\varphi _1$
is not uniquely determined and that the image of
$\varphi _1$
is not uniquely determined and that the image of
![]() $\varphi _2$
in
$\varphi _2$
in
![]() $GL_n(\mathbb {Z}_p)$
is in
$GL_n(\mathbb {Z}_p)$
is in
![]() $GL_n^1(\mathbb {Z}_p)$
. Hence, the profinite subgroup
$GL_n^1(\mathbb {Z}_p)$
. Hence, the profinite subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathrm{Aut}(M)$
generated by
$\mathrm{Aut}(M)$
generated by
![]() $\varphi _1, \varphi _2$
is in fact a pro-p group. Let
$\varphi _1, \varphi _2$
is in fact a pro-p group. Let
be the image of
![]() $\Gamma $
in
$\Gamma $
in
![]() $T_0$
, where
$T_0$
, where
![]() $\psi _i$
is the image of
$\psi _i$
is the image of
![]() $\varphi _i$
in
$\varphi _i$
in
![]() $T_0$
. Thus,
$T_0$
. Thus,
![]() $\Gamma _0$
is a pro-p group.
$\Gamma _0$
is a pro-p group.
By [Reference Romankov21, Proposition 4.4], for every
![]() $\varphi \in \mathrm{IAut}(M)$
for
$\varphi \in \mathrm{IAut}(M)$
for
![]() $\varphi '= \rho ^{ -1} \varphi \rho $
,
$\varphi '= \rho ^{ -1} \varphi \rho $
,
![]() $h'= \mathrm{det} (\beta (\varphi '))$
and
$h'= \mathrm{det} (\beta (\varphi '))$
and
![]() $h = \mathrm{det}( \beta (\varphi ))$
, we have that
$h = \mathrm{det}( \beta (\varphi ))$
, we have that
![]() $h'$
is obtained from h applying the substitution
$h'$
is obtained from h applying the substitution
![]() $s_1 \to s_1 + s_2 + s_1 s_2$
. Then the action of
$s_1 \to s_1 + s_2 + s_1 s_2$
. Then the action of
![]() $\psi _2$
on
$\psi _2$
on
![]() $\psi _1 = [s_1]$
by conjugations is induced by applying the substitution
$\psi _1 = [s_1]$
by conjugations is induced by applying the substitution
![]() $s_1 \to s_1 + s_2 + s_1 s_2$
exactly p-times, i.e., we apply the substitution
$s_1 \to s_1 + s_2 + s_1 s_2$
exactly p-times, i.e., we apply the substitution
Similarly, the action of
![]() $\psi _2^k$
on
$\psi _2^k$
on
![]() $\psi _1 = [s_1]$
by conjugation is induced by applying the substitution
$\psi _1 = [s_1]$
by conjugation is induced by applying the substitution
![]() $s_1 \to s_1 + s_2 + s_1 s_2$
exactly
$s_1 \to s_1 + s_2 + s_1 s_2$
exactly
![]() $pk$
-times, and thus gives the substitution
$pk$
-times, and thus gives the substitution
![]() $s_1 \to (1 + s_1) ( 1 + s_2) ^{pk} -1$
.
$s_1 \to (1 + s_1) ( 1 + s_2) ^{pk} -1$
.
Let A be the normal pro-p subgroup of
![]() $\Gamma _0$
generated by
$\Gamma _0$
generated by
![]() $\psi _1$
. Thus, A can be identified with an additive subgroup of
$\psi _1$
. Thus, A can be identified with an additive subgroup of
![]() $\Delta / p \Delta $
and
$\Delta / p \Delta $
and
The previous paragraph shows that
in particular
![]() $\nu (A)$
and A are infinite.
$\nu (A)$
and A are infinite.
Note that
![]() $\Gamma _0 \simeq A \rtimes D$
, where
$\Gamma _0 \simeq A \rtimes D$
, where
![]() $D \simeq \mathbb {Z}_p $
is generated by
$D \simeq \mathbb {Z}_p $
is generated by
![]() $\psi _2$
. We view A as an
$\psi _2$
. We view A as an
![]() $\mathbb {F}_p[[t]]$
-module via the conjugation action of
$\mathbb {F}_p[[t]]$
-module via the conjugation action of
![]() $\psi _2 = 1 + t$
, where
$\psi _2 = 1 + t$
, where
![]() $\mathbb {F}_p[[t]] \simeq \mathbb {F}_p[[D]]$
. Furthermore, A is a pro-p cyclic
$\mathbb {F}_p[[t]] \simeq \mathbb {F}_p[[D]]$
. Furthermore, A is a pro-p cyclic
![]() $\mathbb {F}_p[[t]]$
-module, with a generator
$\mathbb {F}_p[[t]]$
-module, with a generator
![]() $\psi _1$
. Since every proper
$\psi _1$
. Since every proper
![]() $\mathbb {F}_p[[t]]$
-module quotient of
$\mathbb {F}_p[[t]]$
-module quotient of
![]() $\mathbb {F}_p[[t]]$
is a finite additive group and A is infinite, we deduce that
$\mathbb {F}_p[[t]]$
is a finite additive group and A is infinite, we deduce that
![]() $A \simeq \mathbb {F}_p[[t]]$
. Then, by the example after Theorem 2.2,
$A \simeq \mathbb {F}_p[[t]]$
. Then, by the example after Theorem 2.2,
![]() $\Gamma _0$
is a metabelian pro-p group that is not finitely presented.
$\Gamma _0$
is a metabelian pro-p group that is not finitely presented.
Note that the image W of
![]() $M \simeq \mathrm{Inn} (M)$
in
$M \simeq \mathrm{Inn} (M)$
in
![]() $T_0$
is inside Q and since M is a finitely generated pro-p group and Q is an abelian pro-p group of finite exponent p, then W and consequently
$T_0$
is inside Q and since M is a finitely generated pro-p group and Q is an abelian pro-p group of finite exponent p, then W and consequently
![]() $\Gamma _0 \cap W$
are finite. Since
$\Gamma _0 \cap W$
are finite. Since
![]() $\Gamma _0 \cap W$
is finite,
$\Gamma _0 \cap W$
is finite,
![]() $\Gamma _0/ (\Gamma _0 \cap W)$
is not a finitely presented pro-p group. Actually examining the structure of
$\Gamma _0/ (\Gamma _0 \cap W)$
is not a finitely presented pro-p group. Actually examining the structure of
![]() $\Gamma _0$
, it is easy to see that any finite normal subgroup of
$\Gamma _0$
, it is easy to see that any finite normal subgroup of
![]() $\Gamma _0$
is trivial, in particular
$\Gamma _0$
is trivial, in particular
![]() $\Gamma _0 \cap W = 1$
. Finally,
$\Gamma _0 \cap W = 1$
. Finally,
![]() $\Gamma _0 \simeq \Gamma _0 / (\Gamma _0 \cap W)$
is a metabelian pro-p quotient of a 2-generated pro-p group
$\Gamma _0 \simeq \Gamma _0 / (\Gamma _0 \cap W)$
is a metabelian pro-p quotient of a 2-generated pro-p group
![]() $ H \leq \mathrm{Out}(M)$
. This completes the proof of the lemma.
$ H \leq \mathrm{Out}(M)$
. This completes the proof of the lemma.
Acknowledgments
The author is thankful to the anonymous referee for pointing out a gap in the proof of Proposition 3.4 that was subsequently corrected.