Symposium - International Astronomical Union, The Stability of the Solar System
- This volume was published under a former title. See this journal's title history.
Other
Preface
-
- Published online by Cambridge University Press:
- 14 August 2015, p. vii
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Stability Theory in Celestial Mechanics
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 1-9
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Modern Dynamical Systems Theory
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 11-18
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Other
The Present State of the n-Body Problem
-
- Published online by Cambridge University Press:
- 14 August 2015, p. 19
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Bode's Law
-
- Published online by Cambridge University Press:
- 14 August 2015, p. 21
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Distribution of the Mean Motions of Planets and Satellites and the Development of the Solar System
-
- Published online by Cambridge University Press:
- 14 August 2015, p. 23
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Can the Solar System be Quantized?
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 25-35
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
On the Original Distribution of the Asteroids
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 37-56
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Origin of Commensurabilities in the Satellite Systems
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 57-58
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Origin of the Asteroid Ring
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 59-62
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Orbits of Trojan Asteroids
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 63-69
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Role of Saturn's Oblateness in the Mimas-Tethys Resonance
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 71-76
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Stability of Asteroidal Motion in the Hecuba Gap
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 77-79
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Secular Perturbations for Asteroids Belonging to Families
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 81-82
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Formation of Disks by Inelastic Collisions of Gravitating Particles. Applications to the Dynamics of the Saturn's Ring and to the Formation of the Solar System
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 83-93
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Stationary Solutions of the Averaged Three-Body Problem and Some Problems of Planet Motion Stability
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 95-116
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Integrable Cases of Satellite Problem with the Third Body and the Oblate Planet
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 117-124
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Global Solution in the Problem of the Critical Inclination*
-
- Published online by Cambridge University Press:
- 14 August 2015, pp. 125-127
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Retrograde Satellites in the Circular Plane Restricted Three-Body Problem
-
- Published online by Cambridge University Press:
- 14 August 2015, p. 129
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A Note on a Separation of Equations of Variation of the Elliptic Restricted Three-Body Problem Into Hill's Equations
-
- Published online by Cambridge University Press:
- 14 August 2015, p. 131
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

 of all
of all  is a complete metric space and a generic subset is an open dense subset or an intersection of a countable collection of such open dense subsets of
is a complete metric space and a generic subset is an open dense subset or an intersection of a countable collection of such open dense subsets of  . Some generic properties (i.e. specifying generic subsets) in
. Some generic properties (i.e. specifying generic subsets) in  are described. For instance, generic dynamic systems have isolated critical points and periodic orbits each of which is hyperbolic. If
are described. For instance, generic dynamic systems have isolated critical points and periodic orbits each of which is hyperbolic. If  of all Hamiltonian systems and study corresponding generic properties.
of all Hamiltonian systems and study corresponding generic properties.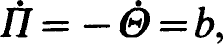 , where
, where