No CrossRef data available.
Article contents
Modern Dynamical Systems Theory
Published online by Cambridge University Press: 14 August 2015
Abstract
In order to analyse generic or typical properties of dynamical systems we consider the space 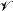 of all C1-vector fields on a fixed differentiable manifold M. In the C1-metric, assuming M is compact,
of all C1-vector fields on a fixed differentiable manifold M. In the C1-metric, assuming M is compact, 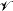 is a complete metric space and a generic subset is an open dense subset or an intersection of a countable collection of such open dense subsets of
is a complete metric space and a generic subset is an open dense subset or an intersection of a countable collection of such open dense subsets of 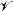 . Some generic properties (i.e. specifying generic subsets) in
. Some generic properties (i.e. specifying generic subsets) in  are described. For instance, generic dynamic systems have isolated critical points and periodic orbits each of which is hyperbolic. If M is a symplectic manifold we can introduce the space
are described. For instance, generic dynamic systems have isolated critical points and periodic orbits each of which is hyperbolic. If M is a symplectic manifold we can introduce the space 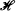 of all Hamiltonian systems and study corresponding generic properties.
of all Hamiltonian systems and study corresponding generic properties.
- Type
- Research Article
- Information
- Symposium - International Astronomical Union , Volume 62: The Stability of the Solar System , 1974 , pp. 11 - 18
- Copyright
- Copyright © Reidel 1974


