In this paper, the author introduces the notion of Ω-Polish spaces (which includes the Polish spaces and a large class of Banach spaces) and extends Castaing's selection theorem (1966) for closed-valued measurable thin multifunctions from a measurable space into an Ω-Polish space. He also extends Robertson's theorem (1974) in the same way.

A chain, or linearly ordered set, is densely subuniform if it is dense and for every order type the elements whose corresponding initial sections have this order type, if any, are dense in the chain. It is uniform if all intial sections are isomorphic. This paper gives constructions for densely subuniform chains which are not uniform. The question arises from the study of congruence-free inverse semigroups, but may also have independent interest.

We shall determine in this paper groups of types Dn, E6, E7 and E8 generated by SU(3, q)'s, q odd, q > 3. These groups are defined in Phan (1975). [We shall refer to this paper as I]. Acquaintance with the results of I is assumed. The identification of groups of type D4 is similar to that of SU(n, q). We actually construct an isomorphism from the universal group of type D4 onto Spin+(8, q). This direct approach does not appear to be feasible for groups of type Dn with n ≧ 5. Fortunately Wong's recent result (1974) is applicable here. But his theorem requires that the characteristic of the field be odd; hence unlike the unitary case, we assume that q is odd and q 3. Using Wong's theorem, we proceed to show by induction that groups of type Dn are homomorphic images of Spin+(2n, q) or Spin −(2n, q) according as n is even or n is odd.

We consider two related classes of groups. For any group G of the first of these — the smallest class containing all finitely generated free groups and closed under cyclic amalgamations — we show that for any U, W ∈ G we can “effectively describe” the set of all x and y with U* and W* conjugate in G. For the second class, which consists of all groups obtained from the first class through cyclic HNN constructions, we solve the conjugacy and power-conjugacy problems.

We discuss properties of arithmetic functions of higher order defined through the introduction of a new concept of divisor of higher order. We shall construct an infinite sequence of Euler-like functions and the well known Euler function will be the first member of this sequence. Asymptotic estimates of such functions are given and a study of error functions associated with the Euler-like sequence is made. We would like to mention that the familiar number theoretic functions become only the first members of an infinite sequence of functions of similar behaviour.

If m and n are natural numbers satisfying 1 ≦ m < n let denote the least integer k such that the statement: ‘Every (0,1) matrix with n columns, with constant row-sum m, and with at least k distinct rows, has rank n’ is true. Then = +1 for m ≧ 2, n ≧ m2 + 2. Further, for 1 ≦ m < n.

The Boolean ring B{M} universal over a meet semilattice M is examined. It is the vector space over the two element field Z2 with base M\{0}. The Z2 linear independence of a meet subsemilattice of a Boolean ring is characterized in order theoretic terms and some ramifications of this on B[M] are considered. The space (ℱpM) of proper filters of M is shown homeomorphic to the Stone space S(B[M]) of B[M] if M has no least element, with ℱP(M) ∪ {M} and S(B[M]) homeomorphic otherwise. The congruence lattice θ(M) of M is compared to the ideal lattice ℱ(B [M]) of B [M] with best results coming if M is a tree with zero when θ (M) = ℐ (B [M]).

If C is a group which satisfies the maximal condition for normal subgroups, then C may be cancelled from a group A in direct products if and only if the infinite cyclic group can be cancelled from A. Finitely generated torsion free nilpotent groups of class 2 satisfy a Remak Krull Schmidt condition.

We give a partial answer to the following questions: Given an additive category and a class of sequences, under what conditions is the universal functor to the abelian category faithful and what other sequences are taken to exact sequences?

The “answers” to these questions appear as theorems 2.2 and 3.2 respectively and amount to a weakening of the condition that there be enough relative projectives.

We then characterize those additive categories with exactness which have the property that all relative exact sequences are determined by a small set of functors into the category of abelian groups.

We establish a version of Bochner Theorem due to S. Boylan for Banch spaces with a basis.

During the last two decades a variety of methods have been developed for the problem of estimation of unknown density f wrt Lebesgue measure and its vth dervative g(= f(v)) using i.i.d random variables X1, …, Xn when X1 ∼ f. For example, see Wegman (1972). In almost all the papers on the estimation of f(x) or g(x), various authors assumed the existence of derivatives of f of order r(>v) at x to obtain rates for the mean-square convergences and other desirable properties for their estimators. Here it is shown that if

then estimators gˇ(x) can be constructed for which E[(gˇ(x)-g(x))2] = O(n−(2a-δ)/(2a+2v+1)) for anygiveng δ > 0. Simiar statements hold for almost sure convergence of gˇ(x). It can also be shown that (gˇ(x1), gˇ(x2)) is asymptotically bivariate normal under certain conditions for x1, ≠ x2. If (Al) is satisfied with a ≦ l, then our estimators have all the desirable properties while other methods are not applicable in this situation since they require differentiability conditions on g. (For example, see Susarla and Kumar (1975) and its references.) Our estimators are defined by using the inversion theorem for some absolutely integrable characteristic functions. The motivation for our estimators is given in O'Bryan and Susarla (1975, 76) and Susarla and O'Bryan (1975).

The inverse semigroup TE of isomorphisms of principal ideals of E onto principal ideals of E, where E is a semilattice, has been introduced and studied by Munn (1966, 1970). He showed that, for any inverse semigroup S with semilattice E, there is a representation of S by an inverse subsemigroup of TE. The Munn representation, however, is not always faithful. In this paper, the possibility is considered of enlarging the carrier set E of the Munn representation in order to obtain a faithful representation of S as an inverse subsemigroup of a structure resembling TE in many ways. A structure X is obtained by replacing each element of E by a set. Then X = ∪{Xe: e ∈ E}, where Xe, denotes some set, has a natural pre-order relation ≤ (where x ≤ y if and only if x ∈ Xe, y ∈ Xf and e ≦ f ) inherited from E such that if T = {(x, y)∈X × X;x ≤ y and y ≤ x} then X/T is isomorphic to E. Such a set X is referred to as a pre-semilattice with semilattice E. If Tx denotes the set of all isomorphisms of principal ideals of X onto principal ideals of X then Tx is an inverse semigroup. Basic properties of Tx are considered. It is shown that when X is locally uniform, that is, when |Xe| = |Xf|, for all e, f ∈ E, Tx may be described as a wreath product of a permutation group with TE.

The set s itself is a presemilattice with semilattice E with respect to the pre-order ≤ defined by a ≤ b if and only if a−1a ≦ b−1b. It is then shown that the Vagner-Preston representation embeds S as a full inverse subsemigroup of Ts. As an application of these concepts the following result is established. Let R and S be inverse semigroups and let θ1(θ2) be an isomorphism of a semilattice E onto the semilattice of R(S). Then there exists a locally uniform presemilattice W and embeddings ϕ1, ϕ2 of R and S, respectively, as full inverse subsemigroups of Tw such that (1) θ1ϕ1 = θ2ϕ2 and (2) (eθ1ϕ1, eθ2ϕ2) ∈ 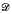if and only if Ee is isomorphic to Ef.

The absence of limit cycles in the system (S): x′ = − y + dx2 + exy + fy2, y′ = x, (′ ≡ d/dt), for 0 ≦ f2 < 2, was shown by Yeh et al. (1963). The general case was established by Kukles and Šakhova using various special results and relying on an extraneous auxiliary system. In this paper we give a new proof of the theorem; in it, we draw mainly on the basic properties of the characteristic exponent of a cycle and use an intrinsic system, viz. the case d = − f(≠ 0) of (S) as an auxiliary system.

Two characterizations of semisimple classes of associative and alternative rings (and semigroups with 0) are given:

(i) A class is a semisimple class if and only if it is hereditary, closed under extensions and subdirect sums;

(ii) A class is a semisimple class if and only if it is hereditary, closed under extensions, and has the co-inductive property.

The first characterization sharpens Armendariz's (1968) result proved for associative rings, the second one is categorically dual to a characterization of radical classes due to Amitsur (1954).

Let E be a real Banach space ordered by a closed, normal and generating cone. Suppose also that the order induced on E has the Riesz decomposition property. It is shown that if T:E → E is a positive linear operator with the property that y, z, a ∈ E with a ≧ Ty, Tz implies there is x ∈ E with x ≧ y, z and a ≧ Tx then the approximate point spectrum and spectrum of T are cyclic subsets of the complex plane. That is, if α = |α|γ lies in one of these sets then so does |α|γk for all integers k.

If is a model with dimension and finite closure, then T() is No-categorical. If is atomic, has dimension and finitely many algebraic elements, then has finite closure or a finite basis. If has finite closure, satisfies the Exchange Lemma, and one-one maps between independent subsets are elementary, then has dimension.

In this paper we define two semigroups of continuous relations on topological spaces and determine a large class of spaces for which Banach-Stone type theorems hold, i.e. spaces for which isomorphism of the semigroups implies homeomorphism of the spaces. This class includes all 0-dimensional Hausdorff spaces and all those completely regular Hausdorff spaces which contain an arc; indeed all of K. D. Magill's S*-spaces are included. Some of the algebraic structure of the semigroup of all continuous relations is elucidated and a method for producing examples of topological semigroups of relations is discussed.

The representation theory of categories is used to embed each promonoidal monad in a monoidal biclosed monad. The existence of a promonoidal structure on the ordinary Eilenberg- Moore category generated by a promonoidal monad is examined. Several results by previous authors (notably A. Kock and F. E. J. Linton) are reproved and extended.

Let p and q be infinite cardinal numbers, p ≧ q, X a set of cardinality p, and BL(X, p, q) the Baer-Levi semigroup of type (p, q) on X. Subsemigroups of BL(X, p, q) are defined and called bounded Baer-Levi semigroups. These semigroups are right simple and are universal in the embedding sense for the class of idempotent-free, right cancellative semigroups S so that any two elements of S have a common right identity in S. Further properties of bounded Baer-Levi semigroups are given and the structure of their lattices of congruences is discussed.

A generalization of Karamata's theorem on integrals of regularly varying functions is proved. Using Laplace-Stieltjes transforms it is shown that any regularly varying function with exponent α (α + 1 ∉ N) is asymptotic to another regularly varying function all of whose derivations are regularly varying.