In this paper we analyze some aspects of the question of using methods from model theory to study structures of functional analysis.
By a well known result of P. Lindström, one cannot extend the expressive power of first order logic and yet preserve its most outstanding model theoretic characteristics (e.g., compactness and the Löwenheim-Skolem theorem). However, one may consider extending the scope of first order in a different sense, specifically, by expanding the class of structures that are regarded as models (e.g., including Banach algebras or other structures of functional analysis), and ask whether the resulting extensions of first order model theory preserve some of its desirable characteristics.
A formal framework for the study of structures based on Banach spaces from the perspective of model theory was first introduced by C. W. Henson in [8] and [6]. Notions of syntax and semantics for these structures were defined, and it was shown that using them one obtains a model theoretic apparatus that satisfies many of the fundamental properties of first order model theory. For instance, one has compactness, Löwenheim-Skolem, and omitting types theorems. Further aspects of the theory, namely, the fundamentals of stability and forking, were first introduced in [10] and [9].
The classes of mathematical structures formally encompassed by this framework are normed linear spaces, possibly expanded with additional structure, e.g., operations, real-valued relations, and constants. This notion subsumes wide classes of structures from functional analysis. However, the restriction that the universe of a structure be a normed space is not necessary. (This restriction has a historical, rather than technical origin; specifically, the development of the theory was originally motivated by questions in Banach space geometry.) Analogous techniques can be applied if the universe is a metric space. Now, when the underlying metric topology is discrete, the resulting model theory coincides with first order model theory, so this logic extends first order in the sense described above. Furthermore, without any cost in the mathematical complexity, one can also work in multi-sorted contexts, so, for instance, one sort could be an operator algebra while another is. say, a metric space.

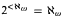 , then for all
, then for all 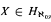 and
and 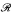 of second order arithmetic into Explicit Mathematics. As a difference from standard
of second order arithmetic into Explicit Mathematics. As a difference from standard 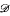 -interpretation, which was used before and was shown to interpret only subsystems proof-theoretically weaker than
-interpretation, which was used before and was shown to interpret only subsystems proof-theoretically weaker than 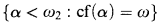
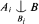 , Second, if
, Second, if 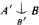 . We prove some positive results in this direction, and we discuss the optimality of these results under ZFC + GCH.
. We prove some positive results in this direction, and we discuss the optimality of these results under ZFC + GCH.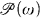 /fin or
/fin or 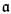 . see Monk [2001].) For brevity we do not consider such generalizations, restricting ourselves to just one cardinal. The set-theoretic generalizations then associate with each infinite cardinal
. see Monk [2001].) For brevity we do not consider such generalizations, restricting ourselves to just one cardinal. The set-theoretic generalizations then associate with each infinite cardinal