This paper is a contribution to the project of determining which set existence axioms are needed to prove various theorems of analysis. For more on this project and its history we refer the reader to [1] and [2].

We work in a weak subsystem of second order arithmetic. The language of second order arithmetic includes the symbols 0, 1, =, <, +, ·, and ∈, together with number variables x, y, z, … (which are intended to stand for natural numbers), set variables X, Y, Z, … (which are intended to stand for sets of natural numbers), and the usual quantifiers (which can be applied to both kinds of variables) and logical connectives. We write ∀x < t φ and ∃x < t φ as abbreviations for ∀x(x < t → φ) and ∃x{x < t ∧ φ) respectively; these are called bounded quantifiers. A formula is said to be 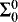if it has no quantifiers applied to set variables, and all quantifiers applied to number variables are bounded. It is 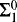if it has the form ∃xθ and it is 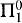if it has the form ∀xθ, where in both cases θ is .

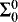The theory RCA0 has as axioms the usual Peano axioms, with the induction scheme restricted to 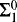formulas, and in addition the 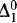comprehension scheme, which consists of all formulas of the form

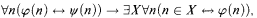
where φ is 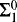, ψ is 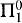, and X does not occur free in φ(n). (“RCA” stands for “Recursive Comprehension Axiom.” The reason for the name is that the 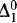comprehension scheme is only strong enough to prove the existence of recursive sets.) It is known that this theory is strong enough to allow the development of many of the basic properties of the real numbers, but that certain theorems of elementary analysis are not provable in this theory. Most relevant for our purposes is the fact that it is impossible to prove in RCA0 that every continuous function on the closed interval [0, 1] attains maximum and minimum values (see [1]).

Since the most common proof of the Mean Value Theorem makes use of this theorem, it might be thought that the Mean Value Theorem would also not be provable in RCA0. However, we show in this paper that the Mean Value Theorem can be proven in RCA0. All theorems stated in this paper are theorems of RCA0, and all of our reasoning will take place in RCA0.