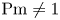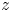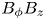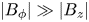In an earlier paper we showed that the combination of azimuthal magnetic fields and super-rotation in Taylor–Couette flows of conducting fluids can be unstable against non-axisymmetric perturbations if the magnetic Prandtl number of the fluid is $\textrm {Pm}\neq 1$. Here we demonstrate that the addition of a weak axial field component allows axisymmetric perturbation patterns for $\textrm {Pm}$ of order unity depending on the boundary conditions. The axisymmetric modes only occur for magnetic Mach numbers (of the azimuthal field) of order unity, while higher values are necessary for the non-axisymmetric modes. The typical growth time of the instability and the characteristic time scale of the axial migration of the axisymmetric mode are long compared with the rotation period, but short compared with the magnetic diffusion time. The modes travel in the positive or negative $z$ direction along the rotation axis depending on the sign of $B_\phi B_z$. We also demonstrate that the azimuthal components of flow and field perturbations travel in phase if $|B_\phi |\gg |B_z|$, independent of the form of the rotation law. Within a short-wave approximation for thin gaps it is also shown (in an appendix) that for ideal fluids the considered helical magnetorotational instability only exists for rotation laws with negative shear.

The global total-$f$ gyrokinetic particle-in-cell code XGC, used to study transport in magnetic fusion plasmas or to couple with a core gyrokinetic code while functioning as an edge gyrokinetic code, implements a five-dimensional continuum grid to perform the dissipative operations, such as plasma collisions, or to exchange the particle distribution function information with a core code. To transfer the distribution function between marker particles and a rectangular two-dimensional velocity-space grid, XGC employs a bilinear mapping. The conservation of particle density and momentum is accurate enough in this bilinear operation, but the error in the particle energy conservation can become undesirably large and cause non-negligible numerical heating in a steep edge pedestal. In the present work we update XGC to use a novel mapping technique, based on the calculation of a pseudo-inverse, to exactly preserve moments up to the order of the discretization space. We describe the details of the implementation and we demonstrate the reduced interpolation error for a tokamak test plasma using first- and second-order elements with the pseudo-inverse method and comparing with the bilinear mapping.

A new algorithm for toroidal flow shear in a linearly implicit, local $\delta f$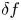 gyrokinetic code is described. Unlike the current approach followed by a number of codes, it treats flow shear continuously in time. In the linear gyrokinetic equation, time-dependences arising from the presence of flow shear are decomposed in such a way that they can be treated explicitly in time with no stringent constraint on the time step. Flow shear related time dependences in the nonlinear term are taken into account exactly, and time dependences in the quasineutrality equation are interpolated. Test cases validating the continuous-in-time implementation in the code GS2 are presented. Lastly, nonlinear gyrokinetic simulations of a JET discharge illustrate the differences observed in turbulent transport compared with the usual, discrete-in-time approach. The continuous-in-time approach is shown, in some cases, to produce fluxes that converge to a different value than with the discrete approach. The new approach can also lead to substantial computational savings by requiring radially narrower boxes. At fixed box size, the continuous implementation is only modestly slower than the previous, discrete approach.

A simplified analytical form of the on-axis magnetic well and Mercier's criterion for interchange instabilities for arbitrary three-dimensional magnetic field geometries is derived. For this purpose, a near-axis expansion based on a direct coordinate approach is used by expressing the toroidal magnetic flux in terms of powers of the radial distance to the magnetic axis. For the first time, the magnetic well and Mercier's criterion are then written as a one-dimensional integral with respect to the axis arclength. When compared with the original work of Mercier, the derivation here is presented using modern notation and in a more streamlined manner that highlights essential steps. Finally, these expressions are verified numerically using several quasisymmetric and non-quasisymmetric stellarator configurations including Wendelstein 7-X.