We investigate the establishment and spread of new adaptive peaks within Wright's ‘shifting balance’. The third phase of the ‘shifting balance’ involves a kind of group selection, since demes in which a superior peak has been established contain more individuals, and so send out more migrants. We assume that population size, N, increases with mean fitness,  , according to the exponential relation,
, according to the exponential relation, 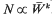 . Here, k is a measure of the weakness of density-dependent regulation, and equals the inverse of the regression of log (fitness) on log(N). In the island model, we find that just as with soft selection (k = 0), two distinct types of behaviour exist: group selection makes no qualitative difference. With low numbers of migrants, demes fluctuate almost independently, and only one equilibrium exists. With large numbers of migrants, all the demes evolve towards the same adaptive peak, and so the whole population can move towards one or other of the peaks. Group selection can be understood in terms of an effective mean fitness function. Its main consequence is to increase the effect of selection relative to drift (Ns), and so increase the bias towards the fitter peak. However, this increased bias depends on the ratio between k and the deme size (k/N), and so is very small when density-dependence is reasonably strong.
. Here, k is a measure of the weakness of density-dependent regulation, and equals the inverse of the regression of log (fitness) on log(N). In the island model, we find that just as with soft selection (k = 0), two distinct types of behaviour exist: group selection makes no qualitative difference. With low numbers of migrants, demes fluctuate almost independently, and only one equilibrium exists. With large numbers of migrants, all the demes evolve towards the same adaptive peak, and so the whole population can move towards one or other of the peaks. Group selection can be understood in terms of an effective mean fitness function. Its main consequence is to increase the effect of selection relative to drift (Ns), and so increase the bias towards the fitter peak. However, this increased bias depends on the ratio between k and the deme size (k/N), and so is very small when density-dependence is reasonably strong.