Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-07-07T15:44:17.262Z Has data issue: false hasContentIssue false
  • English
  • Français

The Weak Type (1, 1) Estimates of Maximal Functions on the Laguerre Hypergroup

Published online by Cambridge University Press:  20 November 2018

Jizheng Huang  and
Liu Heping
Jizheng Huang
Affiliation:
College of Sciences, North China University of Technology, Beijing 100144, China e-mail: [email protected]
Liu Heping
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we discuss various maximal functions on the Laguerre hypergroup $\mathbf{K}$ including the heat maximal function, the Poisson maximal function, and the Hardy–Littlewood maximal function which is consistent with the structure of hypergroup of $\mathbf{K}$. We shall establish the weak type (1, 1) estimates for these maximal functions. The 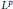${{L}^{p}}$ estimates for 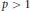$p\,>\,1$ follow fromthe interpolation. Some applications are included.

Keywords

42B2543A62Laguerre hypergroupmaximal functionheat kernelPoisson kernel
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 3 , 01 September 2010 , pp. 491 - 502
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Bloom, W. R. and Heyer, H., Harmonic analysis of probability measures on hypergroups. de Gruyter Stud. Math. 20, de Gruyter, Berlin–New York, 1994.Google Scholar
[2] Dunford, N. and Schwartz, J. T., Linear Operators, Part I. New York, 1958.Google Scholar
[3] Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Tables of integral transforms, Vol. I. McGraw-Hill, New York, 1954.Google Scholar
[4] Folland, G. B. and Stein, E. M., Hardy spaces on homogeneous groups. Princeton University Press and University of Tokyo Press, Princeton, 1982.Google Scholar
[5] Jewett, R. I., Spaces with an abstract converlution of measures. Adv. Math. 18(1975), 1–101. doi:10.1016/0001-8708(75)90002-XGoogle Scholar
[6] Nessibi, M. M. and Trimèche, K., Inversion of the Radon transform on the Laguerre hypergroup by using generalized wavelets. J. Math. Anal. Appl. 208(1997), 337–363. doi:10.1006/jmaa.1997.5299Google Scholar
[7] Stein, E. M., Topics in Harmonic Analysis. Ann. of Math. Stud. 63, Princeton University Press, 1970.Google Scholar
[8] Stein, E. M., Harmonic analysis: real-variable method, orthogonality, and oscillatory integrals. Princeton Univ. Press, 1993.Google Scholar
[9] Stempak, K., An algebra associated with the generalized sub-Laplacian. Studia Math. 88(1988), 245–256.Google Scholar
[10] Stempak, K., Mean summability methods for Laguerre series. Trans. Amer. Math. Soc. 322(1990), 671–690. doi:10.2307/2001720Google Scholar
[11] Thangavelu, S., An introduction to the uncertainty principle. Progr. Math. 217, Birkhäuser, Boston–Basel–Berlin, 2004.Google Scholar
[12] Trimèche, K., Generalized wavelets and hypergroups. Gordon and Breach Science Publishers, Amsterdam, 1997.Google Scholar