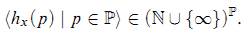We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://ef.msp.org/submit/asl_bsl. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
In this paper, we shall discuss some recent contributions to the project [15, 14, 2, 18, 22, 23] of explaining why no satisfactory system of complete invariants has yet been found for the torsion-free abelian groups of finite rank n ≥ 2. Recall that, up to isomorphism, the torsion-free abelian groups of rank n are exactly the additive subgroups of the n-dimensional vector space ℚn which contain n linearly independent elements. Thus the collection of torsion-free abelian groups of rank at most n can be naturally identified with the set S (ℚn) of all nontrivial additive subgroups of ℚn. In 1937, Baer [4] solved the classification problem for the class S(ℚ)of rank 1 groups as follows.
Let ℙ be the set of primes. If G is a torsion-free abelian group and 0 ≠ x ϵ G, then the p-height of x is defined to be
hx(p) = sup{n ϵ ℕ ∣ There exists y ϵ G such that pny = x} ϵ ℕ ∪{∞}; and the characteristic χ (x) of x is defined to be the function
