A vector measure result is used to study the complementation of the space $K\left( X,Y \right)$ of compact operators in the spaces $W\left( X,Y \right)$ of weakly compact operators, $CC\left( X,Y \right)$ of completely continuous operators, and $U\left( X,Y \right)$ of unconditionally converging operators. Results of Kalton and Emmanuele concerning the complementation of $K\left( X,Y \right)$ in $L\left( X,Y \right)$ and in $W\left( X,Y \right)$ are generalized. The containment of ${{c}_{0}}$ and ${{\ell }_{\infty }}$ in spaces of operators is also studied.

We study the complementation of the space 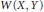$W\left( X,Y \right)$ of weakly compact operators, the space 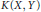$K\left( X,Y \right)$ of compact operators, the space 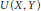$U\left( X,Y \right)$ of unconditionally converging operators, and the space 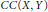$CC\left( X,Y \right)$ of completely continuous operators in the space 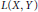$L\left( X,Y \right)$ of bounded linear operators from 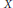$X$ to $Y$. Feder proved that if 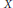$X$ is infinite-dimensional and 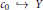${{c}_{0}}\,\to \,Y$, then 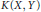$K\left( X,Y \right)$ is uncomplemented in 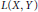$L\left( X,Y \right)$. Emmanuele and John showed that if 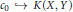${{c}_{0}}\,\to \,K(X,\,Y)$, then 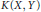$K\left( X,Y \right)$ is uncomplemented in 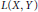$L\left( X,Y \right)$. Bator and Lewis showed that if 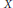$X$ is not a Grothendieck space and 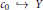${{c}_{0}}\,\to \,Y$, then 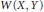$W\left( X,Y \right)$ is uncomplemented in 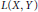$L\left( X,Y \right)$. In this paper, classical results of Kalton and separably determined operator ideals with property 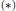$\left( * \right)$ are used to obtain complementation results that yield these theorems as corollaries.

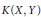
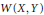
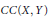
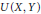
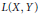
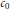
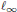
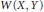
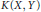
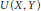
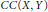
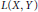
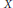
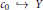
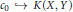
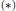
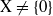This paper contains two results: (a) if is a Banach space and (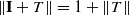L,τ) is a nonempty locally compact Hausdorff space without isolated points, then each linear operator T:C0(L,X)→C0(L,X) whose range does not contain an isomorphic copy of c00 satisfies the Daugavet equality ; (b) if Γ is a nonempty set and X and Y are Banach spaces such that X is reflexive and Y does not contain c0 isomorphically, then any continuous linear operator T:c0(Γ,X)→Y is weakly compact.