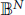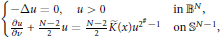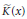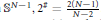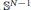We consider the prescribed boundary mean curvature problem in 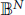${{\mathbb{B}}^{N}}$ with the Euclidean metric

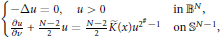$$\{_{\frac{\partial u}{\partial v}+\frac{N-2}{2}u=\frac{N-2}{2}\tilde{K}\left( x \right){{u}^{{{2}^{\#-1}}}}\,\,\,\,\,\,\text{on}{{\mathbb{S}}^{N-1}},}^{-\Delta u=0,\,\,\,\,\,\,u>0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{in}{{\mathbb{B}}^{N}},}$$

where 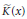$\tilde{K}\left( x \right)$ is positive and rotationally symmetric on 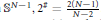${{\mathbb{S}}^{N-1}},{{2}^{\#}}=\frac{2\left( N-1 \right)}{N-2}$. We show that if 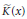$\tilde{K}\left( x \right)$ has a local maximum point, then this problem has infinitely many positive solutions that are not rotationally symmetric on 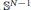${{\mathbb{S}}^{N-1}}$.

Plant growth depends essentially on nutrients coming from the roots and metabolitesproduced by the plant. Appearance of new branches is determined by concentrations ofcertain plant hormones. The most important of them are Auxin and Cytokinin. Auxin isproduced in the growing, Cytokinin in either roots or in growing parts. Many dynamicalmodels of this phenomena have been studied in [1]. In [5], the authors deal with onebranch model. In this work, we focus our interest on a multiple branch model. We deal withthe transport equation in domains of different sizes. A variational reduction type method[3] based on asymptotic partial decomposition introduced in [2] (see also [4]) is used. Inthis work we consider the transport equation in decomposed domain with a general righthand side