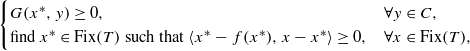This paper deals with the two-level Newton iteration method based on the pressure projection stabilized finite element approximation to solve the numerical solution of the Navier-Stokes type variational inequality problem. We solve a small Navier-Stokes problem on the coarse mesh with mesh size H and solve a large linearized Navier-Stokes problem on the fine mesh with mesh size h. The error estimates derived show that if we choose h = O (|logh|1/2H3), then the two-level method we provide has the same H1 and L2 convergence orders of the velocity and the pressure as the one-level stabilized method. However, the L2 convergence order of the velocity is not consistent with that of one-level stabilized method. Finally, we give the numerical results to support the theoretical analysis.

We introduce augmented Lagrangian methods for solving finite dimensional variational inequality problemswhose feasible sets are defined by convex inequalities, generalizing the proximal augmented Lagrangian methodfor constrained optimization. At each iteration, primal variables are updated by solvingan unconstrained variational inequality problem, and then dual variables are updated through a closed formula.A full convergence analysis is provided, allowing for inexact solution of the subproblems.

We give an explicit Krasnoselski–Mann type method for finding common solutions of the following system of equilibrium and hierarchical fixed points: 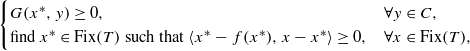where C is a closed convex subset of a Hilbert space H, G:C×C→ℝ is an equilibrium function, T:C→C is a nonexpansive mapping with Fix(T) its set of fixed points and f:C→C is a ρ-contraction. Our algorithm is constructed and proved using the idea of the paper of [Y. Yao and Y.-C. Liou, ‘Weak and strong convergence of Krasnosel’skiĭ–Mann iteration for hierarchical fixed point problems’, Inverse Problems24 (2008), 501–508], in which only the variational inequality problem of finding hierarchically a fixed point of a nonexpansive mapping T with respect to a ρ-contraction f was considered. The paper follows the lines of research of corresponding results of Moudafi and Théra.