1 results
Approximation of subgraph counts in the uniform attachment model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We use Stein’s method to obtain distributional approximations of subgraph counts in the uniform attachment model or random directed acyclic graph; we provide also estimates of rates of convergence. In particular, we give uni- and multi-variate Poisson approximations to the counts of cycles and normal approximations to the counts of unicyclic subgraphs; we also give a partial result for the counts of trees. We further find a class of multicyclic graphs whose subgraph counts are a.s. bounded as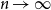
$n\to \infty$.
